Η λύση των προβλημάτων 31-40

Ανδρέας Ιωάννου Κασσέτας

Οι λύσεις των προβλημάτων 31- 40

31. Το μπαλάκι του πινγκ πονγκ

Κρατάει στα χέρια της ένα μπαλάκι του πινγκ πονγκ. Σε κάποια στιγμή το εκτοξεύει προσεκτικά κατακόρυφα προς τα πάνω. Το μπαλάκι ανεβαίνει φθάνει στο ψηλότερο σημείο της τροχιάς και κατεβαίνει. Καμία έκπληξη. Αναρωτιέται εάν βασιζόμενη στη Φυσική θα μπορούσε να συγκρίνει το χρονικό διάστημα της ανόδου με το χρονικό διάστημα της καθόδου. Ξέρει ότι εάν μπορούσε να αγνοήσει την αντίσταση του αέρα τα δύο χρονικά διαστήματα θα ήταν ίσα, όπως συμβαίνει εάν η δοκιμή γίνει στο κενό ή όπως περίπου συμβαίνει εάν το αντικείμενο ήταν σιδερένιο. Τώρα όμως; Τι συμβαίνει με το μπαλάκι του πινγκ πονγκ; Τι την συμβουλεύετε; Πώς μπορεί να βασιστεί στη Φυσική και να δώσει μια απάντηση;

( στον Γιάννη Φιορεντίνο )

Μια λύση.

Εφόσον μας ζητείται να συγκρίνουμε χρονικά διαστήματα, η σκέψη κατευθύνεται στο να εφαρμόσουμε τον δεύτερο νόμο του Νεύτωνα και να τα βγάλουμε πέρα με τη λύση διαφορικών εξισώσεων.

Υπάρχει όμως και μια άλλη σκέψη.

Κατά την εξέλιξη της κίνησης του αντικειμένου, η ενέργεια υποβαθμίζεται. Το άθροισμα κινητικής και δυναμικής ενέργειας συνεχώς μειώνεται. Σε κάθε χρονική στιγμή είναι μικρότερο από την επόμενη .

Σε μια χρονική στιγμή της ανόδου κατά την οποια το μπαλάκι βρίσκεται στη θέση Γ, η ενέργειά του

( άθροισμα κινητικής και βαρυτικής δυναμικής ) είναι μεγαλύτερη από την αντίστοιχη που θα έχει όταν βρεθεί αργότερα βρεθεί στο ίδιο σημείο Γ αλλά σε κάθοδο. Η βαρυτική δυναμική ενέργεια έχει, βέβαια την ίδια τιμή διότι μπαλάκι ξαναβρέθηκε στο ίδιο σημείο Γ. Το συμπέρασμα είναι ότι η κινητική ενέργεια στο σημείο Γ κατά την άνοδό του είναι μεγαλύτερη από την αντίστοιχη που θα έχει στο ίδιο σημείο Γ κατά την κάθοδό του. Το σημείο Γ είναι όμως ένα τυχαίο σημείο Άρα : Σε οποιαδήποτε θέση και να βρεθεί κατά την άνοδό του θα έχει ΜΕΓΑΛΥΤΕΡΗ ΤΑΧΥΤΗΤΑ από αυτή που θα έχει αργότερα, όταν βρεθεί στο ίδιο σημείο κατά την κάθοδο . Κατά την άνοδο θα κινείται πιο γρήγορα .

32. Το αυγό είναι βρασμένο άραγε; 

Δύο αυγά στο τραπέζι. Το ένα είναι βρασμένο σφικτό. Έχει όμως κρυώσει και δεν μπορούμε να το ξεχωρίσουμε με την αφή από το άλλο το άβραστο. Οι παλιοί ξέρουν το «κόλπο». Στριφογυρίζουν και το ένα και το άλλο πάνω στο τραπέζι. Εκείνο που στριφογυρίζει πιο εύκολα και αργεί περισσότερο από το άλλο να σταματήσει είναι το σφιχτοβρασμένο. Για μια ακόμα φορά η ΕΜΠΕΙΡΙΚΗ ΓΝΩΣΗ θριαμβεύει. Τι λένε γι αυτό οι φυσικοί;

( στον Βασίλη Τσελφέ )

Μια απάντηση

Η διαφορά στα δύο αυγά είναι ότι κατά τη στροφική τους κίνηση, το περιεχόμενό του άβραστου μετακινείται- ως προς σύστημα αναφοράς το στρεφομενο κέλυφος -ενώ κάτι παρόμοιο

δεν συμβαίνει με το βρασμένο το περιεχόμενο του οποίου είναι σχεδόν συμπαγές .

Τη σχετική αυτή -ουσιαστικά μη περιγράψιμη -κίνηση του περιεχομένου του άβραστου αυγού εκτός του ότι την υποψιάζεται λογικά, μία συγκεκριμενη εμπειρική παρατήρηση θα ενισχύσει την υποψία του . Εάν, σε κάποια στιγμή, που και τα δύο στρέφονται αργά, αγγίξουμε με το δάκτυλο το σφιχτό, η συνέπεια είναι ότι θα σταματήσει, ενώ εάν κάνουμε το ίδιο με το άβραστο, αυτό θα συνεχίσει να στρέφεται, μήνυμα ότι η εσωτερική σχετική κίνηση του περιεχομένου του επηρεάζεται ελάχιστα .

Η προσεκτική εμπειρική παρατήρηση συδυάζεται με τη θεωρητική σκέψη, με βάση την οποία δημιουργούμε ένα μοντέλο για κάθε περίπτωση.

Η ΕΜΠΕΙΡΙΑ . Επιδιώκουμε να μεταβιβάσουμε την ίδια ποσότητα ενέργειας και στα δύο αυγά , έτσι ώστε να πετύχουμε η κίνηση και των δύο να είναι στροφικη περί κατακόρυφο άξονα . Εννοείται ότι αυτό που τελικά καταφέρνουμε αποκλίνει από το ΜΟΝΤΕΛΟ «στροφική κίνηση» που έχει δημιουργήσει η σκέψη μας . Στο ίδιο αυτό μοντέλο θεωρούμε ότι οι ασκούμενες σε καθένα από τα αυγά εξωτερικές «μη διατηρητικές» δυνάμεις είναι ίδιες . Οι εξωτερικές αυτές δυνάμεις προέρχονται από τον αέρα και από την οριζόντια επιφάνεια του τραπεζιού, ας τις λέμε εξωτερικές αντιστάσεις.

Δοκιμάζουμε πάνω σε οριζόντιο τζάμι, θέτοντας σε περιστροφή και τα δύο αυγά όσο πιο «γρήγορα γίνεται» και διαπιστώνουμε ότι το άβραστο εξ αρχής παρουσιάζει μικρότερη γωνιακή ταχύτητα και στη συνεχει σταματά σε χρονικό διάστημα σαφώς μικρότερο από το σφιχτοβρασμένο. Σε σχετικές μετρήσεις διαπιστώνεται ότι ο λόγος των δύο χρονικών διαστημάτων κυμαίνεται γύρω στο 2 .

Η ΘΕΩΡΗΤΙΚΗ ΣΚΕΨΗ . Η Σκέψη μας διακρίνει ότι η σημαντική διαφορά στην κίνηση κάθε αυγού είναι η εκδήλωση της σχετικής κίνησης του περιεχομένου του ενός, θεωρεί ότι οι συνέπειες είναι δύο

και ότι οι δύο αυτές συνέπειες συνεργάζονται στο να σταματήσει πιο αργά το σφιχτοβρασμένο.

Την πρώτη από τη συνέπειες την περιγράφει με την έννοια ενέργεια και υποστηρίζει ότι

στο άβραστο συμβαίνουν και εσωτερικές μετακινήσεις, η ενέργεια που του μεταβιβάσαμε

αφενός δεν είναι μονο η κινητική ενέργεια λόγω στροφικής κίνησης,

σχετιζόμενη δηλαδή με τη γωνιακή ταχύτητα που παρουσιάζει το κέλυφος, και

αφετέρου η ενέργεια αυτή υποβαθμίζεται με μεγαλύτερο ρυθμό, η μείωση με άλλα λόγια της αρχικής κινητικής ενέργειας δεν οφείλεται μόνο στις εξωτερικές αντιστάσεις,

ενώ στην περίπτωση του σφιχτοβρασμένου η ενέργεια είναι σε κάθε στιγμή μόνο κινητική ενέργεια στρεφομένου στερεού και υποβαθμίζεται μόνο εξ αιτίας των εξωτερικών αντιστάσεων.

Ας δούμε και τη δεύτερη συνέπεια. Αυτή περιγράφεται με την αλλοίωση στην κατανομή της μάζας του άβραστου αυγού και περιγράφεται με την έννοια ροπή αδράνειας .

Η αλλοίωση αυτή εδηλώνεται αρχικά ως αύξηση στη ροπή αδράνειας του άβραστου λόγω της μετακίνησης μέρους από το περιεχόμενο προς την εσωτερική επιφάνεια του δικού του κελύφους . Σύμφωνα με τη Φυσική αυτό συνεπάγεται μια συγκριτικά μεγαλύτερη γωνιακή «επιβράδυνση» - παρά την ισότητα των επιδραδυντικών ροπών κάτι ανάλογο με αυτό που συμβαίνει με την στρεφόμενη χορεύτρια στον πάγο όταν ανοίγει τα χέρια της

Σύμφωνα με τον γενικότερο νόμο για τη στροφική κίνηση ισχύει τ = dL/dt. Το τ συμβολίζει την ολική εξωτερική ροπή, την προερχόμενη από τις πάσης φύσεως μη διατηρητικές εξωτερικές αντιστάσεις και το L τη στιγμιαία στροφορμή του συστήματος. Θεωρώντας ότι διατηρείται

ένας σταθερός άξονας περιστροφής τ = dL/dt τ = Ιdω/dt + ωdI/dt τ = Ια_γων + ωdI/dt οπότε

για το σφιχτοβρασμένο αυγό με τη σταθερή ροπή αδράνειας ως προς τον άξονα περιστροφής έστω Ι₀ ισχύει ωdI/dt = 0 άρα τ = Ι₀α_γων1

και για το άβραστο τ = Ια_γων2 + ωdI/dt , όπου α_γων1 και α_γων2 είναι οι αντίστοιχες αλγεβικές τιμές για καθεμιά από τις

γωνιακές «επιβραδύνουσες» επιταχύνσεις και ω η αλγεβρική τιμή της γωνιακής ταχύτητας

Εφόσον θεωρούμε ίδια την εξωτερική ροπή θα είναι Ι₀α_γων1 = Ια_γων2 + ωdI/dt α_γων1 = α_γων2Ι/ Ι₀ + (ω/Ι₀) (dI/dt) με dI/dt > 0

Αν θεωρήσουμε άξονα z με τα θετικά προς την κατεύθυνση της γωνιακής ταχύτητας

Άρα ως συνέπεια της αύξησης της ροπής αδράνειας το άβραστο αυγό εκδηλώνει, αρχικά τουλάχιστον, μεγαλύτερη γωνιακή επιβάδυνση γεγονός το οποίο,συνεργαζόμενο με την «κατανομή» της αρχικά μεταβιβαζόμενης ενέργειας και με τη συγριτικά μεγαλύτερη ενεργειακή υποβάθμιση, συμβάλλει στο να σταματήσει πιο γρήγορα

Πρέπει να ομολογήσουμε ότι το φαινόμενο , στη συνολική του εξέλιξη δεν μπορoύμε να το περιγράψουμε με κάποια μαθηματική συνάρτηση, λύση αντίστοιχης διαφορικής εξίσωσης. Κι αυτό δεν συμβαίνει μόνο με το άβραστο αυγό. Για τα περισσότερα από «αυτά που συμβαίνουν», αφού τα παρατηρήσουμε προσεκτικά και τα επαναλάβουμε όσο καλύτερα γίνεται, μετρούμε κάποιες μετρήσιμες ποσότητες τις οποίες έχουμε επιλέξει , δημιουργούμε ΜΟΝΤΕΛΑ, επινοούμε κατάλληλες έννοιες , εφαρμόζουμε γενικότερους νόμους και, με τη βοήθεια των μαθητικών, καταλήγουμε σε συμπεράσματα τα οποία ενίοτε προσεγγίζουν τη «χυμώδη» Πραγματικότητα. Αυτός είναι εξάλλου και ο πυρήνας της φυσικής

33. Οι ποδηλάτισσες 

Ευρείς λεωφόρους διασχίζουν

φευγαλέα οι ποδηλάτισσες

Οδυσσέας Ελύτης

Το ομώνυμο μυθιστόρημα της Ρέας Σταθοπούλου αρχίζει με τον στίχο του Οδυσσέα Ελύτη για τις ποδηλάτισσες. Όσο για μας τους γένους αρσενικού είναι γεγονός ότι το «μαγικό» αυτό δίτροχο του εφηβικού μας σύμπαντος μάς προκαλούσε δέος. Όταν δεν έτρεχε έπεφτε και δεν έπεφτε μόνο όταν το κέντρο μάζας του είχε μια ταχύτητα αξιοπρεπή. Ανεξήγητο για όποιον δεν έχει συναντηθεί με τη Φυσική ή ξέρει μόνο από Μηχανική του υλικού σημείου. Δύο είναι οι βασικές έννοιες με τις οποίες χρειάζεται να είναι εξοικειωμένος, η στροφορμή και η ροπή και οι δύο μεγέθη διανυσματικά πράγμα που σημαίνει ότι για να κατανοήσει κανείς τις παραξενιές του ποδηλάτου πρέπει να διαθέτει και κάποια χωρική νοημοσύνη, spatial intelligence όπως τη λέει ο Gardner. Η μεταβολή της στροφορμής ( ως προς κάποιο σημείο ) είναι ίση με την ώθηση της συνολικής ροπής (ως προς το ίδιο σημείο) μας λέει η Μηχανική του rigid body.

Ας φανταστούμε ένα τροχό ποδηλάτου ακίνητο με τον άξονά της περιστροφής του οριζόντιο. Αν ασκήσουμε μια δύναμη στον άξονα θα τον δούμε να στρέφεται απολύτως αναμενόμενα. Αν όμως έχουμε θέσει σε περιστροφή τον τροχό ΜΕ ΤΟΝ ΑΞΟΝΑ ΟΡΙΖΟΝΤΙΟ και ασκήσουμε στον άξονα μια δύναμη ΚΑΤΑΚΟΡΥΦΗ αυτό που θα συμβεί θα μας εντυπωσιάσει. Ο άξονας του τροχού ΘΑ ΣΤΡΑΦΕΙ ΣΕ ΟΡΙΖΟΝΤΙΟ ΕΠΙΠΕΔΟ. Και οι φυσικοί το αιτιολογούν με βάση τις γεωμετρικές ιδιαιτερότητες της ροπής. Πώς ακριβώς;

Εφόσον το ποδήλατο είναι ακίνητο και το αφήσουμε θα ανατραπεί. Η ροπή του βάρους λένε οι φυσικοί. Εάν όμως βρίσκεται σε κίνηση έχει ήδη στροφορμή και -εφόσον γύρει- η ροπή του «κατακόρυφου» βάρους προσθέτει οριζόντια στροφορμή στην ήδη υπάρχουσα.

Πώς θα μπορούσαμε να κάνουμε ένα σχήμα και να τα παραστήσουμε όλα αυτά την οριζόντια δηλαδή στροφορμή του τροχού κάθετα στην κίνηση και την οριζόντια -κατά τη διεύθυνση της κίνησης- στροφορμή η οποία προστίθεται διανυσματικά στην αρχική

( στη Ρέα Σταθοπούλου Παλαιοπούλου )

Μια απάντηση .

Ο νόμος για τη στροφική κίνηση . Δεν διατυπώθηκε από τον Newton, βασίστηκε όμως στον δεύτερο νευτωνικό νόμο για την κίνηση και διατυπώθηκε από τον Lenhard Euler ( Λέναρντ Όιλερ) με τη βοήθεια των εννοιών ροπή δύναμης, ροπή της ορμής ( στροφορμή ) και ροπή αδράνειας. τ = dL/dt

Ένα θεώρημα που απορρέει από τον γενικό αυτό νόμο μας λέει πώς

όταν εκδηλωθεί μια ροπή ( ως προς σημείο ) με συνιστώσα τ ΚΑΤΑ τον άξονα z , κατά το στοιχειώδες χρονικό διάστημα dt που θα ακολουθήσει μεταβιβάζεται στροφορμή με συνιστώσα στον z

ίση με την « ώθηση ροπής», ίση δηλαδή με το γινόμενο τdt,

Όταν το σύστημα είναι ακίνητο, η δράση στον οριζοντιο άξονα περιστροφής του (xx’ )

μιας κατακορυφης δύναμης προκαλεί μια ροπή ως προς το κέντρο μάζας

διάνυσμα οριζόντιο, με φορέα στον yy’ - κάθετον στον xx’ -

οπότε το σύστημα στρέφεται

«αναμενόμενα» περί τον οριζόντιο άξονα yy’’,

κάνει ότι θα έκανε μια οριζόντια ράβδος, αποκτά στροφορμή ΚΑΤΑ τον yy’

Όταν ο τροχός στρέφεται, η δράση της δύναμης

έχει σαν συνέπεια την εκδήλωση μιας παρόμοιας ροπής, οπότε μεταβιβάζεται στροφορμή

( ώθηση της ροπής, τdt = dL, λένε οι φυσικοί ) κατά τον άξονα yy’

Σε αυτή την περίπτωση βέβαια –

κατα την οποία ο τροχός έχει ήδη στροφορμή L₁-

η μεταβιβαζόμενη στοφορμή L₂ , διάνυσμα οριζόντιο κατά τον yy’ ,

προστίθεται διανυσματικα στην αρχική L₁ και η νέα στροφορμή

είναι ένα διάνυσμα οριζόντιο , άθροισμα δύο καθέτων διανυσμάτων .

34. Από ξύλο και από χάλυβα 

Ο χάρακας είναι ο μισός ξύλινος και ο μισός χαλύβδινος. Στην πρώτη δοκιμή στερεώνεται

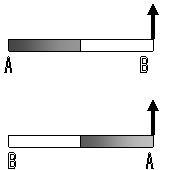με το χαλύβδινο άκρο του σε άρθρωση και έτσι ώστε να μπορεί

να στραφεί σε κατακόρυφο επίπεδο

ενώ στο ξύλινο άκρο του ασκείται κατακόρυφη δύναμη προς τα πάνω

και αποκτά επιτάχυναη α_γων1.

Στη δεύτερη δοκιμή ο χάρακας αναστρέφεται και στηρίζεται

στην ίδια άρθρωση με το ξύλινο άκρο του, ασκείται η ίδια δύναμη

στο άλλο του άκρο και η γωνιακή επιτάχυναη α_γων2.

Να συγκρίνετε τις τιμές των α_γων1 και α_γων2.

Ο χάρακας να θεωρηθεί μονοδιάστατη ράβδος και καθένα από τα δύο του κομμάτια ομογενές.

( στον Θανάση Χριστοφιλόπουλο )

Σύμφωνα με τον νόμο για τη στροφική κίνηση για σώμα με σταθερή ροπή αδράνειας

τ₁ = Ι₁ α_γων1 και τ₂ = Ι₂ α_γων2τ₁ = τ₂

Εφόσον τ₁ = τ₂ θα είναι α_γων2/ α_γων1 = Ι₁/ Ι₂

Θεωρούμε m₁ και m₂ τις μάζες από χάλυβα και από ξύλο αντίστοιχα , L το μήκος κάθε τμήματος άρα 2L το μήκος κάθε ράβδου . Για το κάθε τμήμα μήκους m και μάζας L, η ροπή αδράνειας ως προς άξονα καθετο στη διεύθυνση του ο οποίος διέρχεται από το κέντρο μαζας ισχύε Ι_cm = 1/12 mL² .

Σύμφωνα και με το θεώρημα των παραλλήλων αξόνων - θεώρημα Steiner –

Για τον στερεωμένο στο Α χάρακα η ως τον άξονα περιστροφής Α ροπή αδράνειας είναι

α. για το τμήμα ΑΓ 1/12 m₁L² + m₁L²/4 = 1/3 m₁L²

β. για το τμήμα ΓΒ 1/12 m₂L² + m₂ 9L²/4 = 7/3 m₂L²

οπότε Ι₁ = 1/3 m₁L² + 7/3 m₂L²

Για τον στερεωμένο στο Β χάρακα η ως τον άξονα περιστροφής Β ροπή αδράνειας είναι

α. για το τμήμα ΒΓ 1/12 m₂L ² + m₂L²/4 = 1/3 m₂L²

β. για το τμήμα ΓΒ 1/12 m₁ L ² + m₁ 9L²/4 = 7/3 m₁L²

οπότε Ι₂ = 1/3 m₂L² + 7/3 m₁L²

Εάν θέσουμε m₁/ m₂ = λ

εφόσον m₁είναι η μάζα του χαλύβδινου και m₁η μάζα του ξύλινου λ> 1

Ι₁ = 1/3 λm₂L² +7/3 m₂L² Ι₂ = 1/3 m₂L² + 7/3 λm₂L²

oπότε ο λόγος των ροπών αδράνειας θα είναι Ι₁ /Ι₂ = (7+λ)/ (7λ+1)

Και εφόσον λ > 1 θα είναι (7+λ)/ (7λ+1) < 1 άρα Ι₁ /Ι₂< 1 και

α_γων2/α_γων1 < 1 α_γων2< α_γων1

35. Το γεωμετρικό σημείο «κέντρο μάζας»

Θεωρούμε ένα σύστημα δύο κινουμένων υλικών σημείων σε πεδίο βαρύτητας έντασης g .

Η μάζα m του συστήματος είναι ίση με το άθροισμα των μαζών των υλικών σημείων.

Το κέντρο μάζας του συστήματος είναι ένα ΓΕΩΜΕΤΡΙΚΟ ΣΗΜΕΙΟ

το οποίο σε κάθε στιγμή έχει μία θέση και μια ταχύτητα υ_cm.

Με ποια από τα παρακάτω συμφωνείτε;

α. Η ορμή του συστήματος είναι ίση με την ορμή ενός υλικού σημείου με μάζα ίση με τη μάζα m του συστήματος και ταχύτητα ίση με την ταχύτητα του κέντρου μάζας. p = mυ_cm.

β. Η κινητική ενέργεια του συστήματος είναι ίση με την κινητική ενέργεια που θα είχε ένα υλικό σημείο μάζας ίσης με τη συνολική μάζα m του συστήματος ταχύτητα ίση με την ταχύτητα του κέντρου μάζας . K = ½mυ_cm².

γ. Η – ως προς κάποια οριζόντια επιφάνεια – βαρυτική δυναμική ενέργεια του συστήματος των υλικών σημείων είναι ίση με τη δυναμική ενέργεια – ως προς την οριζόντια επιφάνεια - που θα είχε ένα υλικό σημείο μάζας m που θα βρισκόταν στη θέση που βρίσκεται το κέντρο μάζας . U = mgh_cm_.

( στη Τζένη Τσιτοπούλου )

Η απάντηση

Συμφωνούμε με τα α. και γ.

36.Η σφήνα και το βαρίδι 

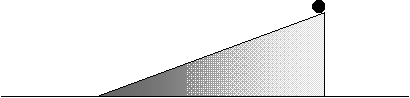
Η ομογενής ξύλινη σφήνα έχει μάζα Μ και μπορεί να ολισθαίνει πάνω σε οριζόντια επιφάνεια. Στην κορυφή της βάζουμε ένα βαρίδι μάζας m και το αφήνουμε να γλιστρήσει στην κεκλιμένη πλευρά της.

Η σφήνα κινείται με επιτάχυνση, ως προς το έδαφος, α_σφ και το βαρίδι κατεβαίνει προς τη βάση με επιτάχυνση ως προς τη σφήνα α_//.

Δίνεται το ύψος Η από το έδαφος στο οποίο αφήνεται το βαρίδι και η γωνία φ της κεκλιμένης επιφάνειας με το οριζόντιο επίπεδο.

Το βαρίδι θεωρείται σημειακό αντικείμενο και η τριβή αμελητέα

Αν οι μάζες των δύο αντικειμένων είναι ίσες να προσδιορίσετε.

α. τον λόγο α_///α_σφ

β. τις τιμές των α_// και α_σφ

γ. την τροχιά του κέντρου μάζας του συστήματος

δ. την κινητική ενέργεια του συστήματος τη στιγμή που το βαρίδι φθάνει στη βάση

ε. το «πότε θα φθάσει» το βαρίδι στη βάση

στ. το «πού θα βρίσκεται» η σφήνα τη στιγμή που το βαρίδι φθάνει στη βάση

Να προσδιορίσετε όλα τα προηγούμενα στη γενική περίπτωση που ο λόγος Μ/m είναι λ.

( στον Βασίλη Γεωργουσόπουλο)

Μια λύση

Θεωρώ την κίνηση της σφήνας ως παρατηρητής στο έδαφος.

Συμβολίζω τη μάζα της με m. Οι ασκούμενες δυνάμεις είναι α. το βάρος της mg ,

η κατακόρυφη N΄ από το έδαφος και η αντίδραση της δύναμης Ν την οποία της ασκεί το βαρίδι.

Η, ως προς το έδαφος, επιτάχυνσή της είναι οριζόντια

Εφαρμόζω τον δεύτερο νόμο

στο μεταφορικά κινούμενο σώμα σφήνα.

Η επιτάχυνση α_σφτου κέντρου μάζας του είναι οριζόντια.

Νημφ = mα_σφ

Θεωρώ την κίνηση που κάνει το βαρίδι ως παρατηρητής στο έδαφος

Οι ασκούμενες στο βαρίδι δυνάμεις .

Είναι το βάρος του mg και η - μέτρου N - κάθετη δύναμη από τη σφήνα .

Η επιτάχυνσή του.

Εφόσον η , ως προς τη σφήνα, επιτάχυνσή του είναι α_// , η ως προς το έδαφος επιτάχυνσή του θα είναι το διανυσματικό άθροισμα της α_//

(παράλληλης προς την επιφάνεια το κεκλιμένου)

και της οριζόντιας προς τα δεξιά α_σφ

Εφαρμόζω τον δεύτερο νόμο της κίνησης στο βαρίδι .

Επιλέγω άξονα x οριζόντιο και άξονα y κατακόρυφο

ΣF_x = ma_xΝημφ = mα_//συνφ - mα_σφ

Από τις δύο εξισώσεις προκύπτει mα_σφ= mα_//συνφ - mα_σφ

Άρα 2α_σφ= α_//συνφ και α_///α_σφ = 2/συνφ.

Για το ίδιο σώμα και για τον κατακόρυφο άξονα

ΣF_y = ma_y mg – Nσυνφ = mα_//ημφ. Από το συνδυασμό της εξίσωσης αυτής με τις προηγούμενες προκύπτουν οι τιμές των α_// και α_σφ. Η τροχιά του κέντρου μάζας όλου του συστήματος θα είναι η τροχιά ενός υποθετικού υλικού σημείου στο οποίο θα δρούσαν όλες οι εξωτερικές δυνάμεις που δρουν στο σύστημα. Οι εξωτερικές αυτές δυνάμεις είναι το ολικό βάρος 2mg και η δύναμη Ν΄ από το έδαφος. Είναι όλες κατακόρυφες άρα η τροχιά θα είναι κατακόρυφη αλλά με επιτάχυνση η οποία δεν είναι ίση με g. Αν υπολογίσουμε την τιμή Ν΄ - με την εξίσωση ΣF_y= 0 για το σώμα σφήνα – θα μπορέσουμε να βρούμε και την τιμή της επιτάχυνσης του κέντρου μάζας.

Ένας παρατηρητής κινούμενος με την επιταχυνόμενη κίνηση της σφήνας μπορεί από την τιμή της σχετικής επιτάχυνσης α_//και από το μήκος του κεκλιμένου επιπέδου να προσδιορίσει πότε το σφαιρίδιο θα φθάσει στο έδαφος.

36.Η σφήνα και το βαρίδι 

Η σφήνα κινείται με επιτάχυνση α_σφ και το βαρίδι κατεβαίνει προς τη βάση με επιτάχυνση ως προς τη σφήνα α_//.

Δίνεται το ύψος Η από το έδαφος στο οποίο αφήνεται το βαρίδι και η γωνία φ της κεκλιμένης επιφάνειας με το οριζόντιο επίπεδο. Το βαρίδι θεωρείται σημειακό αντικείμενο και η τριβή αμελητέα

Αν οι μάζες των δύο αντικειμένων είναι ίσες να προσδιορίσετε.

α. τον λόγο α_///α_σφ ( Απ: 2/συνφ)

β. τις τιμές των α_// και α_σφ

γ. την τροχιά του κέντρου μάζας του συστήματος

δ. την κινητική ενέργεια του συστήματος τη στιγμή που το βαρίδι φθάνει στη βάση

ε. το «πότε θα φθάσει» το βαρίδι στη βάση

στ. το «πού θα βρίσκεται» η σφήνα τη στιγμή που το βαρίδι φθάνει στη βάση

Να προσδιορίσετε όλα τα προηγούμενα στη γενική περίπτωση που ο λόγος Μ/m είναι λ.

( στον Βασίλη Γεωργουσόπουλο)

Μια λύση

Θεωρώ την κίνηση της σφήνας ως παρατηρητής στο έδαφος

Οι ασκούμενες δυνάμεις είναι α. το βάρος της, η κατακόρυφη N΄ από το έδαφος και η αντίδραση της δύναμης Ν την οποία της ασκεί το βαρίδι.

Η ως προς το έδαφος επιτάχυνσή της είναι οριζόντια

Εφαρμόζω τον δεύτερο νόμο στο σώμα σφήνα

Νημφ = mα_σφ

Θεωρώ την κίνηση που κάνει το βαρίδι ως παρατηρητής στο έδαφος

Οι ασκούμενες στο βαρίδι δυνάμεις .

Είναι το βάρος του mg και η κάθετη N από τη σφήνα .

Η επιτάχυνσή του.

Συμμετέχει στην κίνηση της σφήνας άρα η επιτάχυνσή του είναι το διανυσματικό άθροισμα της α_// ( παράλληλης προς την επιφάνεια το κεκλιμένου ) και της οριζόντιας προς τα δεξιά α_σφ

Εφαρμόζω τον δεύτερο νόμο στο βαρίδι .

Επιλέγω άξονα x οριζόντιο και άξονα y κατακόρυφο

ΣF_x = ma_xΝημφ = mα_//συνφ - mα_σφ

Από τις δύο εξισώσεις προκύπτει mα_σφ= mα_//συνφ - mα_σφ

Άρα 2α_σφ= α_//συνφ και α_///α_σφ = 2/συνφ.

Για το ίδιο σώμα και για τον κατακόρυφο άξονα

ΣF_y = ma_y mg – Nσυνφ = mα_//ημφ. Από το συνδυασμό της εξίσωσης αυτής με τις προηγούμενες προκύπτουν οι τιμές των α_// και α_σφ. Η τροχιά του κέντρου μάζας θα είναι η τροχιά ενός υποθετικού υλικού σημείου στο οποίο θα δρούσαν όλες οι εξωτερικές δυνάμεις που δρουν στο σύστημα. Οι εξωτερικές αυτές δυνάμεις είναι το ολικό βάρος 2mg και η δύναμη Ν΄ από το έδαφος. Είναι όλες κατακόρυφες άρα η τροχιά θα είναι κατακόρυφη αλλά με επιτάχυνση η οποία δεν είναι ίση με g. Αν υπολογίσουμε την τιμή Ν΄ - με την εξίσωση ΣF_y= 0 για το σώμα σφήνα – θα μπορέσουμε να βρούμε και την τιμή της επιτάχυνσης του κέντρου μάζας.

37. Γλιστράει στον τοίχο και στο πάτωμα. 

Η ομογενής ράβδος ΑΒ , μήκους L, βρίσκεται αρχικά ακίνητη σε κατακόρυφη θέση, πλάι στον τοίχο και αρχίζει να ολισθαίνει χωρίς τριβή έτσι ώστε να στηρίζεται

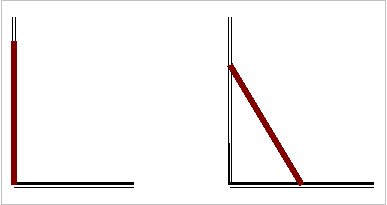
γλιστρώντας τόσο στον τοίχο όσο και στο έδαφος. Σας ζητούμε:

α. Να προσδιορίσετε τη μορφή της τροχιάς του κέντρου μάζας

β. Να θεωρήσετε την κίνηση στροφική περί στιγμιαίο οριζόντιο άξονα περιστροφής διερχόμενο από σημείο Δ του κατακόρυφου επιπέδου και να προσδιορίσετε την τροχιά του σημείου Δ κατά την ολίσθηση της ράβδου.

γ. Να θεωρήσετε την κίνηση σύνθετη προερχόμενη από μία μεταφορική και από μία στροφική κίνηση περί άξονα που διέρχεται από το κέντρο μάζας και να προσδιορίσετε τόσο την ταχύτητα υ_Α_στρ του άκρου Α λόγω της στροφικής κίνησης όσο και την ταχύτητα υ_Αμεττου Α λόγω της μεταφορικής κίνησης σε χρονική στιγμή που η ολισθαίνουσα ράβδος σχηματίζει με το έδαφος γωνία φ.

δ. Να προσδιορίσετε τις γωνίες που σχηματίζουν σε κάθε χρονική στιγμή της κίνησης οι ταχύτητες υ_Α_στρ και υ_Αμεττου Α με την κατακόρυφο.

ε. Να συγκρίνετε την ταχύτητα του Α με την ταχύτητα του Β την ίδια χρονική στιγμή

στ. Να προσδιορίσετε τις ταχύτητες του κέντρου μάζας και των άκρων Α και Β τη στιγμή που η ράβδος σχηματίζει με το οριζόντιο έδαφος γωνία φ.

[ υ_cm² = 3gL(1-ημφ)/4 ) υ_Α² = 3gLσυν²φ( 1-ημφ) υ_Β² = 3gLημ²φ( 1-ημφ) ]

ζ. Να προσδιορίσετε την κεντρομόλο και την επιτρόχιο επιτάχυνση του κέντρου μάζας κατά τη στιγμή που η ολισθαίνουσα ράβδος σχηματίζει με το έδαφος γωνία φ.

[ α_κ,_cm = 3g ( 1- ημφ ) / 2 α_ε,_cm = 3g συνφ / 4 ]

η. Να προσδιορίσετε τις ταχύτητες του κέντρου μάζας και των σημείων Α και Β κατά τη στιγμή που η ράβδος «προσγειώνεται» στο έδαφος και οριζοντιώνεται.

( στον Πάνο Μουρούζη )

α. Η τροχιά του κέντρου μάζας θα είναι ΚΥΚΛΙΚΗ. Καθώς ολισθαίνει η ομογενής ράβδος το κέντρο μάζας, το γεωμετρικό δηλαδή σημείο που είναι το μέσον της, απέχει από το τη γωνία Ο σταθερή απόσταση ίση με L/2, το μισό μήκος της ράβδου. Κι αυτό το δείχνει η Γεωμετρία. Η απόσταση 0Κ είναι ίση με το μισό της υποτείνουσας του ορθογωνίου τριγώνου ΑΟΒ. Το κέντρο μάζας διαγράφει τόξο 90⁰ και ακτίνας L/2 με κέντρο το σημείο Ο.

β. Ένας τρόπος για να περιγράψουμε την κίνηση της ράβδου είναι να την «δούμε» ως στροφική με στιγμιαίο άξονα περιστροφής διερχόμενο από σημείο Δ. Κατά την κίνηση της ράβδου η ταχύτητα του σημείου Α είναι διαρκώς κατακόρυφη ενώ τη ταχύτητα του Β είναι διαρκώς οριζόντια. Σε τυχαία χρονική στιγμή της κίνησης – γωνία φ ως προς τον ορίζοντα - το σημείο Δ από το οποίο θα διέρχεται ο στιγμιαίος άξονας περιστροφής, κατά τη στιγμή εκείνη, προσδιορίζεται αν φέρουμε ΚΑΘΕΤΟ στη ράβδο στο σημείο Α και μία άλλη κάθετη στη ράβδο στο σημείο Β. Το σημείο τομής των δύο καθέτων είναι το σημείο Δ. Κατά την εξέλιξη της κίνησης, η απόσταση του Δ από το σημείο Ο είναι σταθερή ίση με το μήκος L της ράβδου. Η τροχιά συνεπώς του Δ θα είναι κυκλική ακτίνας L με κέντρο το Ο, σε τόξο 90⁰ . Για την ταχύτητα του σημείου Α θα ισχύει υ_Α = ω_σαπ . (ΑΔ) ενώ για την ταχύτητα του Β θα ισχύει υ_Β = ω_σαπ .(ΒΔ). Το σύμβολο ω_σαππαριστάνει τη στιγμιαία γωνιακή ταχύτητα ως προς τον στιγμιαίο άξονα περιστροφής.

Από τις δύο σχέσεις προκύπτει υ_Β/υ_Α= εφφ. Είναι και η απάντηση στο ερώτημα ε.

γ. Ένας άλλος τρόπος για να περιγράψουμε την κίνηση της ράβδου είναι να την «αναλύσουμε» σε μία ΜΕΤΑΦΟΡΙΚΗ με την ταχύτητα υ_cm του κέντρου μάζας και από μία ΣΤΡΟΦΙΚΗ περί οριζόντιο άξονα που διέρχεται από το κέντρο μάζας .

Εφόσον η τροχιά του κέντρου μάζας είναι ΚΥΚΛΙΚΗ, η ταχύτητα υ_cm του κέντρου μάζας είναι ΚΑΘΕΤΗ στη διάμεσο ΟΚ, άρα- την τυχαία στιγμή που ράβδος σχηματίζει με τον ορίζοντα γωνία φ- το διάνυσμα της υ_cm σχηματίζει με την κατακόρυφο γωνία φ

Η κίνηση του σημείου Α. Η κατακόρυφη ταχύτητα του σημείου Α θα είναι διανυσματικό άθροισμα της ταχύτητας υ_Αμετ = υ_cm – λόγω μεταφορικής - και της ταχύτητας υ_Αστρλόγω της στροφικής περί το κέντρο μάζας. Το μέτρο της υ_Αστρ θα είναι ίσο με ωL/2 όπου ω η γωνιακή ταχύτητα λόγω της στροφικής περί κέντρο μάζας . υ_Αστρ = ωL/2. Το διάνυσμα της υ_Αστρ κάθετο στη ράβδο σχηματίζει με την κατακόρυφο γωνία θ ( 90-φ ) ΙΣΗ με εκείνη που σχηματίζει με την κατακόρυφο και το διάνυσμα της υ_cm . Στο παραλληλόγραμμο των δύο διανυσμάτων η διαγώνιος ( που παριστάνει το διανυσματικό τους άθροισμα) θα είναι η κατακόρυφη υ_Α α. Αυτό σημαίνει ότι η 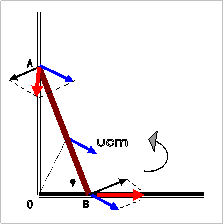κατακόρυφη θα είναι διχοτόμος της γωνίας του παραλληλογράμμου, το παράλληλο θα είναι ρόμβος με συνέπεια τα μέτρα των να είναι ίσα υ_Αστρ και υ_cm να είναι ίσα . υ_Αστρ = υ_cm

Η συνισταμένη των υ_Αστρ και υ_cm , διαγώνιος του παραλληλογράμμου, θα είναι υ_Α = 2υ_cm συνφ

Αντίστοιχα γι την ταχύτητα υ_Β ως διανυσματικό άθροισμα των υ_cm και υ_Βστρ αποδεικνύεται υ_Β = 2υ_cm ημφ. Το σχετικό παραλληλόγραμμο είναι ρόμβος και η γωνίες των δύο ταχυτήτων με την συνισταμένη οριζόντια υ_Β είναι ίσες και καθεμία τους 90-φ

Η τιμή της υ_cm σε τυχαία στιγμή της κινησης ( γωνία φ με τον ορίζοντα) μπορεί να υπολογιστεί εάν εφαρμόσουμε ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΕΝΕΡΓΕΙΑΣ κατά την κίνηση της ράβδου και την εξίσωση που θα προκύψει τη συνδυάσουμε με τα παραπάνω.

mgL/2 + O = ½ mυ_cm² + ½ I_cmω² + mgL/2ημφ . Εφόσον I_cm = 1/12mL² και υ_cm = ωL/2

mgL/2( 1- ημφ) = 2/3mυ_cm²υ_cm² = 3gL(1-ημφ)/4 .

υ_Α² = 3gLσυν²φ( 1-ημφ) υ_Β² = 3gLημ²φ( 1-ημφ)

Τη στιγμή που η ράβδος γίνεται οριζόντια υ_cm² = 3gL/4

38. Ο κύλινδρος μαζί και το στεφάνι 

Ένας συμπαγής κύλινδρος συνδέεται αξονικά με ένα λεπτό στεφάνι μέσω μιας αβαρούς ράβδου. Το σύστημα αφήνεται από ένα ύψος πάνω σε κεκλιμένη επιφάνεια γωνίας θ με το στεφάνι χαμηλότερα. Με δεδομένο ότι ο κύλινδρος και το στεφάνι έχουν το ίδιο βάρος Β και την ίδια ακτίνα σας ζητούμε να προσδιορίσετε:

α. τη δύναμη την οποία ασκεί το στεφάνι στην αβαρή ράβδο

β. την επιτάχυνση του κέντρου μάζας του κυλίνδρου

γ. την ταχύτητα του κέντρου μάζας του κυλίνδρου τη στιγμή που έχει μετακινηθεί κατά d από τη θέση που τον αφήσαμε.

( στον Μαρίνη Πετρόπουλο )

Αν αφήναμε τα δύο αντικείμενα ελεύθερα, χωρίς να τα συνδέουμε, «σε αγώνα δρόμου», ο κύλινδρος με τη συγκριτικά μικρότερη ροπή αδράνειας ( Ι_cm = ½m R²) θα κατηφοριζε πιο γρήγορα από το στεφάνι ( Ι_cm = mR²)

Αυτό το αποδείξαμε, βασιζόμενοι στους νόμους της κίνησης, στο πρόβλημα 22.

Αν λοιπόν τα συνδέσουμε αξονικά με τη ράβδο αμελητέας μάζας και τα αφήσουμε να κατηφορίσουν μαζί , με πρώτο το στεφάνι, ο πιο βιαστικός κύλινδρος θα ΣΠΡΩΧΝΕΙ , μέσω της ράβδου σύνδεσης το προπορευόμενο στεφάνι.

( Εάν βάζαμε πρώτο τον κύλινδρο θα συνέβαινε το αντίθετο )

Για τη μεταφορική κίνηση της ράβδου

Το σώμα ράβδος εκτελεί μεταφορική κίνηση με την κοινή επιτάχυνση των δύο κέντρων μάζας (δίσκου και δακτυλίου και εφόσον η μάζα του ΘΕΩΡΕΙΤΑΙ ΑΜΕΛΗΤΕΑ, ενώ η επιτάχυνσή του ΕΙΝΑΙ διάφορη του μηδενός, – η συνισταμένη των δυνάμεων πρέπει, βάση του δεύτερου νομου της κίνησης - να είναι ΑΜΕΛΗΤΕΑ και να θεωρηθεί ίση με μηδέν . Οι δυνάμεις που ασκούνται στη ράβδο είναι δύο . Η δύναμη που της ασκεί ο κύλινδρος και η δύναμη που τις ασκεί το στεφάνι. Οι δύο αυτές δυνάμεις πρέπει συνεπώς, βάσει του δεύτερου νόμου να είναι αντίθετες και η περίπτωση να είναι αντιπαράλληλες συνιστώντας ζεύγος αποκλείεται διότι σε αυτή την περίπτωση η κίνηση δεν θα ήταν μεταφορική. Εφόσον λοιπόν και οι δύο ασκούνται σε σημεία του γραμμικού μονοδιάστατου αντικειμένου ράβδος οι φορείς και των δύο δυνάμεων θα συμπίπτουν με την «ευθεία» της ράβδου .

Με βάση και τον τρίτο νόμο, η δύναμη F_ρστεφ που ασκεί η ράβδος στο στεφάνι και η δύναμη F_ρκύλ που ασκεί η ράβδος στον κύλινδρο θα έχουν ίσα μέτρα (έστω F) και κατευθύνσεις αντίθετες .

Για την κύλιση του σώματος κύλινδρος

Η κατεύθυνση της δύναμης που ασκεί ο κύλινδρος στη ράβδο θα είναι τέτοια ώστε να περιγράφεται το ότι ο

« πιο βιαστικός» κύλινδρος σπρώχνει τη ράβδο. Άρα η αντίδρασή της η δύναμη, δηλαδή, F_ρκύλ που ασκεί η ράβδος στον πιο βιαστικό κύλινδρο θα έχει κατεύθυνση αντίθετη προς εκείνη της ταχύτητας του κέντρου μάζας

Έστω το μέτρο της F . Σχετικά με την κίνηση του κέντρου μάζας

mgημθ – F - Τ₂ = ma_cm

Για τη «συνιστώσα» στροφική κίνηση Τ₂R = I₂a_γων Τ₂R = ½ mR²a_γων

και δεδομένου ότι a_cm= Ra_γων Τ₂ = ½ ma_cmΑπό τις σχέσεις αυτές προκύπτει

mgημθ – F = 3/2ma_cm(1) .

Για την κύλιση του σώματος στεφάνι

Η ασκούμενη στο στεφάνι δύναμη F_ρστεφ – εκ μέρους της ράβδου –

έχει αντίθετη κατεύθυνση από τη F_ρκυλ αλλά το μέτρο της θα είναι F .

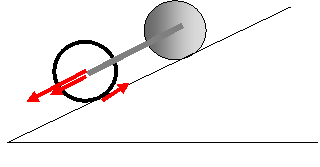Για την κίνηση του κέντρου μάζας mgημθ + F – Τ₁ = ma_cm

Για τη «συνιστώσα» στροφική κίνηση Τ₁R = I₁a_γων

Τ₁R = mR²a_γων Τ₁ = ma_cm

Από τις σχέσεις αυτές προκύπτει

mgημθ + F = 2 ma_cm(2) .

Από τις (9) και (10)

Μετά από διαίρεση κατά μέλη F = mgημθ/7 Προκύπτει επίσης a_cm= 4gημθ/7

Η ταχύτητα του κέντρου μάζας

Η ζητούμενη ταχύτητα του κέντρου μάζας του κυλίνδρου, μετά από μετατόπιση d μπορεί να προσδιοριστεί

α. Με συνδυασμό της τιμής της επιτάχυνσης -η οποία προσδιορίστηκε με εφαρμογή των νόμων της κίνησης - με τις εξισώσεις για την ευθύγραμμη κίνηση του γεωμετρικού σημείου κέντρο μάζας d = ½ at² και υ = αt οπότε υ² = 2αd και τελικά υ² = 8gημθd/7

β. Με εφαρμογή της διατήρησης της ενέργειας για το σύστημα.

Η κινητική ενέργεια του συστήματος, σε μια χρονική στιγμή που η ταχύτητα του κέντρου μάζας είναι υ, είναι

Κ = (½mυ² + ½ Ι_cm₁ω²) +(½mυ² + ½ Ι_cm₂ω²) Κ = ½mυ²+ ½ mR²ω² +½ mυ² + ½ ½ mR²ω²

Εφόσον η κύλιση κάθε σώματος είναι χωρίς ολίσθηση υ = Rω οπότε Κ = 7mυ²/4

Σύμφωνα με τη διατήρηση της ενέργειας του συστήματος U₀ + Κ₀= U + Κ

2mgdημθ + 0 = 0 + 7mυ²/4 υ² = 8gημθd/7

Παρατήρηση. Η κατεύθυνση αλλά και η τιμή της δύναμης που ασκεί η ράβδος στο στεφάνι μπορεί να προσδιοριστεί και με εφαρμογή του θεωρήματος έργου ενέργειας στο στεφάνι.

Η κινητική ενέργεια μετά από μετατόπιση d είναι Κ = ½ mυ² + ½ Ι_cmω² = ½ mυ² + ½ mR²ω²

Κ = mυ² και, εφόσον για την ταχύτητα ισχύει υ² = 8gημθd/7 , Κ = 8mgημθd/7.

Σύμφωνα με το «θεώρημα» τόσο είναι και το άθροισμα των έργων των ασκουμένων δυνάμεων

Το έργο της βαρος είναι mgdημθ – και εφόσον το ολικό έργο είναι 8mgημθd/7 – το έργο της σταθερής F είναι ΘΕΤΙΚΟ και ίσο με mgημθd/7.

Η ασκούμενη συνεπώς F έχει την κατεύθυνση της μετατόπισης και μέτρο mgημθ/7

39. Αγώνας δρόμου των δύο ισοβαρών 

Το σύστημα αφήνεται από μια θέση ελεύθερο από μια θέση έτσι ώστε το αβαρές νήμα

να είναι τεντωμένο και οριζόντιο

και η τροχαλία ακριβώς στο μέσο της απόστασης

των δύο αντικειμένων.

Τα δύο αντικείμενα έχουν ίσες μάζες

και θεωρούνται σημειακά .

Το Α κατευθύνεται προς την τροχαλία

και το Β προς ένα σημείο της κατακόρυφης πλευράς του τραπεζιού.

Ποιο θα φθάσει πρώτο

στο σημείο που κατευθύνεται; ( από το περιοδικό QUANTUM)

( στον Αλέκο Μάμαλη )

Μια λύση

Να φανταστούμε την ευθύγραμμη κίνηση που εκτελεί η προβολή κάθε σώματος σε οριζόντιο επίπεδο.

Οι δύο προβολές κινούνται προς αντίθετες κατευθύνσεις.

Η προβολή του Α έχει ως επιτάχυνση της προβολή της επιτάχυνσής του.

Είναι ίση με την προβολή της ασκούμενης στο Α ολικής δύναμης στο Α προς τη μάζα του Α.

Η ολική αυτή δύναμη είναι ίση με τη δύναμη που ασκεί το νήμα στο Α. α_Α = Ν/m.

Αντίστοιχα η επιτάχυνση του Β θα είναι ίση α_Β = N΄x/m = N΄ημφ/m, όπου φ η γωνία του νήματος με την κατακόρυφο. Εφόσον το νήμα έχει αμελητέα μάζα ισχύει N΄= N,

άρα -εκτός από τη χρονική στιγμή μηδέν- σε κάθε επόμενη χρονική στιγμή

η επιτάχυνση του Α θα είναι μεγαλύτερη που θα έχει το Β την ίδια στιγμή.

Άρα τη στιγμή που το Α θα φθάσει στην τροχαλία και η προβολή του θα έχει μετατοπιστεί

κατά το μισό του ολικού μήκους του νήματος, το Β δεν θα βρίσκεται ακόμα

στην κατακόρυφη πλευρά το τραπεζιού.

39. Οι φυσικοί διαφωνούν στον πρασινοπίνακα 

Η μπίλια κυλίεται χωρίς ολίσθηση σε οριζόντια επιφάνεια. Το Α που είναι και το μοναδικό σημείο επαφής με την οριζόντια επιφάνεια έχει εξ ορισμού μηδενική ταχύτητα. Πως μπορούμε να προσδιορίσουμε την επιτάχυνση του σημείου Α;

Το συζητούν δύο φυσικοί. Λέει ο Σάββας : «Βασίλη το σημείο Α «έχει» επιτάχυνση.

Το αρνείται ο Βασίλης. «Το μηδενικής ταχύτητας Α δεν έχει επιτάχυνση. Κοίτα ρε Σάββα εάν θεωρήσουμε την κίνηση της μπίλιας σύνθετη προερχόμενη από σύνθεση μιας μεταφορικής με την επιτάχυνση του κέντρου μάζας και μιας στροφικής περί άξονα που διέρχεται από το κέντρο μάζας θα . . . . . . . . πρέπει να κάνω ένα σχήμα . Παίρνει μια λευκή κιμωλία και κάνει ένα σχήμα στον πίνακα. Χρησιμοποιεί και κόκκινη για τις επιταχύνσεις και

συνεχίζει «Λόγω της μεταφορική κίνησης η επιτάχυνση του Α είναι ίση με εκείνη του κέντρου μάζας και λόγω της στροφικής κίνησης η επιτάχυνση του ίδιου σημείου είναι αντίθετη. Κατά συνέπεια η ολική επιτάχυνση είναι μηδέν».

Ο Σάββας όμως παρεμβαίνει « Ξέρεις κάτι, Βασίλη, ξέχασες ότι λόγω της στροφικής κίνησης το σημείο Α έχει και κεντρομόλο επιτάχυνση .» Παίρνει κιμωλία μπλε χρώματος και συμπληρώνει στο σχήμα

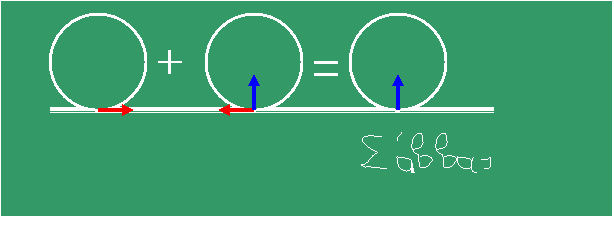
«Και, τελικά, η μπλε επιτάχυνση θα είναι η ολική επιτάχυνση του σημείου Α».

Ο Βασίλης όμως δεν το βάζει κάτω « Μα η μπλε επιτάχυνση στην οποία καταλήγεις είναι κεντρομόλος επιτάχυνση και ΔΕΝ ΕΙΝΑΙ ΔΥΝΑΤΟΝ ΕΝΑ ΣΗΜΕΙΟ ΜΗΔΕΝΙΚΗΣ ΤΑΧΥΤΗΤΑΣ, όπως είναι το Α, ΝΑ ΕΧΕΙ ΚΕΝΤΡΟΜΟΛΟ ΕΠΙΤΑΧΥΝΣΗ».

Ο Σάββας τον κοιτάζει σκεπτικός. Ποιος νομίζετε ότι έχει δίκιο;

(στον Βαγγέλη Καραλή)

Η απάντηση

Έχει δίκιο ο Σάββας. Όταν αναλύουμε την κίνηση του Α σε ευθύγραμμη και κυκλική, η «μπλε» επιτάχυνση ΛΕΙΤΟΥΡΓΕΙ ως κεντρομόλος στην κυκλική «συνστώσα» της κίνησης .

Όταν κάποιος παρατηρητής στο έδαφος αντικρίζει την κίνηση του Α (χωρίς να την αναλύει σε συνιστώσες κινήσεις )

η τροχιά του Α είναι κυκλοειδής και η «μπλε» επιτάχυνση ΕΙΝΑΙ «η επιτάχυνση του σημείου Α».

Τη στιγμή εκείνη η ταχύτητα είναι μηδέν και η επιτάχυνση έχει ρόλο επιτρόχιας.

Αν ήταν μηδέν, το σημείο δεν θα μπορούσε να συνεχίσει την κυκλοειδή κίνησή του .

Κάτι ανάλογο, σε ευθύγραμμη κίνηση, παρατηρείται όταν εκτοξεύουμε μία «σημειακή» πέτρα κατακόρυφα προς τα πάνω και εκείνη βρίσκεται στο ανώτερο σημείο της τροχιάς. Η ταχύτητα είναι μηδενική αλλά η πέτρα έχει επιτάχυνση .

Ο Βασίλης έχει δίκιο όταν ισχυρίζεται ότι «ένα σημείο μηδενικής ταχύτητας δεν είναι δυνατόν να έχει κεντρομόλο επιτάχυνση» αλλά τελικά έχει δίκιο ο Σάββας διότι κατά την κίνηση του Α - ως προς παρατηρητή στο έδαφος- η μπλε επιτάχυνση δεν λειτουργεί ως κεντρομόλος.

40. Η κατακόρυφη ράβδος 

Σε μία ομογενή κατακόρυφο ράβδο αναρτημένη από το ανώτερο σημείο της Ο και αρχικώς ακίνητη ασκείται οριζόντια δύναμη F στο κατώτερο σημείο της Α

1. Οι ασκούμενες στη ράβδο δυνάμεις ανάγονται σε ζεύγος

2. Οι ασκούμενες στη ράβδο δυνάμεις ανάγονται σε μία οριζόντια δύναμη F

διερχόμενη από το κέντρο μάζας και σε ένα ζεύγος δυνάμεων

3. Οι ασκούμενες στη ράβδο δυνάμεις ανάγονται στην ασκούμενη

στο σημείο Α δύναμη F και σε ζεύγος δυνάμεων

4. Η ασκούμενη στη ράβδο δύναμη στο σημείο Ο είναι κατακόρυφη

5. Η ασκούμενη στη ράβδο δύναμη στο σημείο Ο έχει οριζόντια συνιστώσα

με κατεύθυνση αντίθετη της F

6. Η επιτάχυνση του κέντρου μάζας θα είναι ίση με F/m όπου m η μάζα της ράβδου

7. Η επιτάχυνση του κέντρου μάζας θα έχει συνιστώσα προς το σημείο ανάρτησης Ο

Με ποια από τα παραπάνω συμφωνείτε;

Η ροπή αδράνειας της ράβδου ως προς άξονα κάθετο σε αυτήν - διερχόμενο από το κέντρο μάζας - είναι ίση με mL²/12

( στον Πέτρο Βατούγιο )

Μια λύση .

Το σημείο Ο διατηρείται αμετακίνητο .

Η δράση της οριζόντιας δύναμης στο σημείο Α σημαίνει και ολική ροπή ως προς Ο .

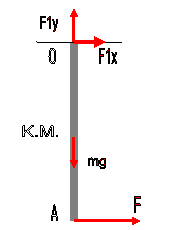Η δράση συνεπώς της F , συνεπάγεται στροφορμή ως προς Ο.

Η ράβδος θα αρχίσει να στρέφεται περί Ο.

Τη στιγμή εκείνη ισχύει FL = Ι_o a_γων

Ι_o = 1/3 mL² ½Lα_γων = α_cm_{,
επιτροχια}

α_cm_,
επιτρ = 3F/2m

Το κέντρο μάζας θα έχει τη στιγμή εκείνη επιτρόχια επιτάχυνση. 3F/2m

Η επιτρόχια αυτη οριζόντια επιτάχυνση

είναι η ολική επιτάχυνση του κέντρου μάζας

δεδομένου ότι ένα σημείο μηδενικής ταχύτητας

δεν έχει κεντρομόλο επιτάχυνση. α_cm= 3F/2m

1. Οι ασκούμενες στη ράβδο δυνάμεις ανάγονται σε ζεύγος

Δεν είναι σωστό . Αν συνέβαινε, το κέντρο μάζας θα είχε μηδενική επιτάχυνση

2. Οι ασκούμενες στη ράβδο δυνάμεις ανάγονται σε μία οριζόντια δύναμη F

Δεν είναι σωστό . Αν συνέβαινε, το κέντρο μάζας θα είχε οριζόντια επιτάχυνση F/m

3. Οι ασκούμενες στη ράβδο δυνάμεις ανάγονται στην ασκούμενη

στο σημείο Α δύναμη F και σε ζεύγος δυνάμεων

Δεν είναι σωστό . Αν συνέβαινε, το κέντρο μάζας θα είχε οριζόντια επιτάχυνση F/m

4. Η ασκούμενη στη ράβδο δύναμη στο σημείο Ο είναι κατακόρυφη

Δεν είναι σωστό . Αν συνέβαινε, το κέντρο μάζας θα είχε οριζόντια επιτάχυνση F/m

5. Η ασκούμενη στη ράβδο δύναμη στο σημείο Ο έχει οριζόντια συνιστώσα

με κατεύθυνση αντίθετη της F

Δεν είναι σωστό . Το κέντρο μάζας έχει οριζοντια επιτάχυνση 3F/2m,

μεγαλύτερη από όση θα είχε εάν δρούσε μόνο η F.

Η επιτάχυνση αυτή

διαμορφώνεται, συνεπώς,

και από τη δράση άλλης οριζόντιας δύναμης με ίδια

κατεύθυνση με εκείνη της F .

Η μόνη από τις ασκούμενες δυνάμεις

που μπορεί να είναι οριζοντια

είναι η συνιστώσα F₁_x της ασκούμενης

στο Ο δύναμης F₁ .

Για επιτάχυνση του κέντρου μάζας ισχύει F + F₁_x = ma_cm

F + F₁_x = m3F/2m F₁_x =F/2

6. Η επιτάχυνση του κέντρου μάζας θα είναι ίση με F/m όπου m η μάζα της ράβδου

Δεν είναι σωστό . Είναι ίση με 3F/2m

7. Η επιτάχυνση του κέντρου μάζας θα έχει συνιστώσα προς το σημείο ανάρτησης Ο.

Δεν είναι σωστό . Μια τέτοια συνιστώσα θα ήταν κεντρομόλος συνιστώσα

και αυτό δεν μπορεί να συμβεί σε σημείο αρχικώς ακίνητο .