Ανδρέας Ιωάννου Κασσέτας

 

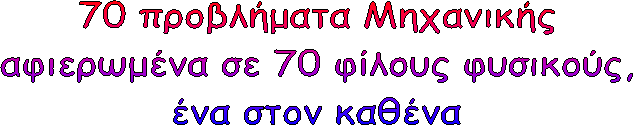
70 προβλήματα Μηχανικής αφιερωμένα σε 70 φίλους φυσικούς, ένα στον καθένα

 

 

 

 

 

 

1.  Οι παγοδρόμοι και το κοντάρι.        ˜˜˜

Δύο παγοδρόμοι,  καθένας από τους οποίους έχει μάζα 70 kg, πλησιάζουν κατά μήκος παράλληλων τροχιών που απέχουν 3 μέτρα με ταχύτητες αντίθετων κατευθύνσεων και ίσων μέτρων 10 m/s . Ο πρώτος κρατάει από την άκρη ένα αβαρές κοντάρι μήκους 3 μέτρων διατηρώντας το κάθετο στην ταχύτητά του. Τη στιγμή που οι παγοδρόμοι φθάνουν στη μικρότερη μεταξύ τους απόσταση ο δεύτερος πιάνει το κοντάρι από το ελεύθερο άκρο. 

α. Να περιγράψετε την κίνηση των δύο παγοδρόμων από τη στιγμή που ο δεύτερος πιάνει το κοντάρι    β. Τραβώντας το κοντάρι οι παγοδρόμοι μειώνουν την απόστασή τους στο ένα μέτρο. Πώς θα είναι τότε η κίνησή τους;       γ. Κατά πόσο μεταβάλλεται η κινητική ενέργεια του συστήματος πριν και μετά την αλλαγή την ελάττωση της απόστασης των δύο παγοδρόμων λόγω του ότι τράβηξαν το κοντάρι. Θεωρούμε την τριβή αμελητέα.   

(στον Ανδρέα Βαλαδάκη )

 

2. Αν κοπεί ο σπάγκος.            ˜˜˜

 

Οι μάζες των ατσάλινων σφαιρών Σ1, Σ2 και Σ2 είναι 60 g,  20 g και 60 g αντίστοιχα. Το φυσικό μήκος του ελατηρίου είναι 14 cm η σταθερά του 150 N/m και το μήκος του σπάγκου 12 cm. Η τριβή θεωρείται αμελητέα και η οποιαδήποτε κρούση μεταξύ των σφαιρών θεωρείται κεντρική και ελαστική.

Οι σφαίρες Σ1 και Σ2 συνδέονται με τον αβαρή σπάγκο, χωρίς να έχουν προσδεθεί στο ελατήριο με συνέπεια το ελατήριο να είναι συσπειρωμένο και ο σπάγκος τεντωμένος. Η σφαίρα Σ3, βρίσκεται ακίνητη προς το μέρος της Σ2 σε απόσταση 75 cm από αυτήν.

                          Σε κάποια στιγμή κόβουμε τον σπάγκο και οι δύο σφαίρες Σ1 και Σ2 απωθούνται και - καθώς το ελατήριο δεν είναι προσδεμένο σε καμία από αυτές - απομακρύνονται. Σας ζητούμε

α. να υπολογίσετε την επιτάχυνση της Σ2 κατά τη στιγμή που έχουμε κόψει τον σπάγκο 

β.  να υπολογίσετε την ταχύτητα της  Σ2  όταν το ελατήριο αποκτά  το φυσικό του μήκος 

γ. να υπολογίσετε την απόσταση των  Σ1 και Σ2 τη στιγμή που η Σ2 έχει φθάσει στη Σ3 .

δ. να προσδιορίσετε την ταχύτητα της Σ3 μετά την κρούση

( στον Νίκο Δαπόντε )

 

3. Η μπίλια στη λεκάνη   ˜˜˜˜  

Μια μπίλια μάζας m και ακτίνας R αφήνεται από ένα σημείο Α αμετακίνητης ημισφαιρικής λεκάνης ακτίνας 6R και κυλάει προς τη βάση της λεκάνης χωρίς ολίσθηση. Τη στιγμή που αφήνεται η ευθεία κέντρο μπίλιας- κέντρο λεκάνης σχηματίζει με την κατακόρυφο γωνία 600.

α. Κατά τη στιγμή που αφήνεται η κάθετη δύναμη αντίδραση που της ασκεί η λεκάνη είναι ίση με ½ mg.

β. Σε μια τυχαία στιγμή της κίνησης η στατική τριβή είναι ίση με 2/7mgημθ, όπου η γωνία που σχηματίζει  η ευθεία κέντρο μπίλιας- κέντρο λεκάνης με την κατακόρυφο

γ. Κατά τη στιγμή που φθάνει στη βάση της λεκάνης για την   ταχύτητα του κέντρου μάζας είναι ισχύει υ2 = 25gR/7.

δ. Κατά τη στιγμή που φθάνει στη βάση της λεκάνης η  κάθετη δύναμη την οποία ασκεί η μπίλια στη λεκάνη είναι 12mg/7.

ε. Κατά τη στιγμή που φθάνει στη βάση της λεκάνης η στατική τριβή είναι μηδέν

στ. Για να πραγματοποιηθέι η κύλιση χωρίς ολίσθηση ο συντελεστής στατικής τριβής είναι μεγαλύτερος από 2Ö3/7

( στον Κώστα Γεωργακόπουλο )

 

4. Η πιο μεγάλη συσπείρωση   ˜˜˜˜

Τα δύο αντικείμενα έχουν ίσες μάζες και βρίσκονται σε οριζόντιο τραπέζι χωρίς τριβή. Το Α κινείται με ταχύτητα υ προς το αρχικώς ακίνητο Β το άκρο του οποίου συνδέεται με ελατήριο αμελητέας μάζας και βρίσκεται προς το μέρος του σώματος Α. Το Α προσπίπτει πάνω στο ελατήριο.  Να υπολογίσετε τη μέγιστη συσπείρωση του ελατηρίου και την  τελική ταχύτητα κάθε σώματος. Δίνονται η σταθερά του ελατηρίου και η μάζα κάθε σώματος.

 

( στον Δημήτρη Αγγελίδη )

 

5. Με μεγάλη ταχύτητα ανατρέπεται.     ˜˜˜˜

Ένα αντικείμενο σε σχήμα κύβου πλευράς α ολισθαίνει κατά μήκος κεκλιμένου επιπέδου γωνίας 150 φθάνει στη βάση με ταχύτητα υ και ανατρέπεται.

 

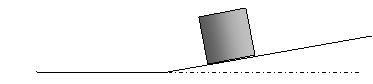
Να προσδιορίσετε την τιμή της ταχύτητας υ ώστε να γίνει η ανατροπή. Η ροπή αδράνειας του κύβου πλευράς α και μάζας m ως προς άξονα συμμετρίας που περνάει από το κέντρο μάζας είναι ίση με 1/6 mα2.                 υmin  = 0,713Öαg

( στην ’λκηστη Ζερβοπούλου )

 

6. Στεφάνι στην  ανηφοριά            ˜˜˜˜

Ένα στεφάνι καθώς κυλίεται χωρίς να ολισθαίνει με ταχύτητα κέντρου μάζας υ0  .

συναντά κεκλιμένο επίπεδο γωνίας 450 και συνεχίζει να κινείται σε αυτό ανερχόμενο με αρχική ταχύτητα κέντρου μάζας υ.

Να προσδιορίσετε τον λόγο υ/υ0.                     (λ = 0,853 )

( στον Γιώργο Φασουλόπουλο )

 

7. Προς τα που ασκείται η δύναμη;    ˜˜˜˜

Η ομογενής ράβδος έχει μάζα m και μήκος  L,  αρθρώνεται στο κάτω άκρο της  με ακίνητο στήριγμα Ο. Αρχικά είναι κατακόρυφη και δεχόμενη ασήμαντη ώθηση αρχίζει να στρέφεται σε κατακόρυφο επίπεδο. Να προσδιορίσετε τη δύναμη που ασκεί η άρθρωση Ο  στη ράβδο κατά τη στιγμή που η ράβδος περνά από την οριζόντια θέση. Η ροπή αδράνειας της ράβδου ως  προς τον άξονα περιστροφής είναι ίση με 1/3mL2.

 

                                        

( στον ’γγελο Μπάτρη  )

 

8. Το ένα ευρώ και ο χάρακας           ˜˜˜˜

Ένας ομογενής χάρακας  μάζας Μ και μήκους L βρίσκεται αρχικώς ακίνητος σε λείο οριζόντιο τραπέζι και μπορεί να κινείται με οποιονδήποτε τρόπο. Ένας δίσκος θεωρούμενος σημειακό αντικείμενο μάζας m, κινούμενος πάνω στο τραπέζι χωρίς τριβή με ταχύτητα υ, προσπίπτει κάθετα στον ακίνητο χάρακα και σε σημείο που απέχει d από το μέσον του χάρακα.  Η κρούση θεωρείται ελαστική.

a. O δίσκος μετά την κρούση θα παραμείνει ακίνητος μόνο εφόσον κτυπήσει στο μέσον

β. O δίσκος μετά την κρούση θα παραμείνει ακίνητος εφόσον η μάζα του είναι ίση με

ML2/( L2+ 12d2) ανεξάρτητα από την τιμή της ταχύτητας με την οποία θα χτυπήσει τον χάρακα

 

                 

γ. O δίσκος μετά την κρούση θα παραμείνει ακίνητος εφόσον η μάζα του είναι ίση με τη μάζα του χάρακα ανεξάρτητα από το «που» θα τον κτυπήσει

δ. Είναι αδύνατον ο δίσκος μετά την κρούση να παραμείνει ακίνητος διότι έτσι παραβιάζεται κάποιος νόμος της Φυσικής

( στον Παναγιώτη Σκούντζο )

 

9. Το τριγωνάκι για τα κάλαντα     ˜˜˜

Χρησιμοποιώντας  σκληρό ισοπαχές σύρμα φτιάχνουμε ένα τριγωνάκι με ίσες πλευρές σαν αυτό που έχουν  τα παιδιά για τα κάλαντα .

            

                

Α. Αν είναι m η μάζα κάθε πλευράς του τριγώνου και α το μήκος της, με ποιο από τα παρακάτω συμφωνείτε;

η  ροπή αδράνειας του τριγώνου ως προς άξονα z που περνάει από το σημείο τομής των διαμέσων και είναι κάθετος στο επίπεδο είναι      α. ίση με 1/3 ma2      

β. ίση με ¼ ma2 

γ. Μεγαλύτερη από τη ροπή αδράνειας ως προς άξονα παράλληλο προς τον z και διερχόμενο από μια κορυφή του τριγώνου      

δ. ίση  με ½ ma2

Β. Κρεμάμε το μάζας 3m τριγωνάκι από οριζόντιο καρφί από την κορυφή Α,  έτσι ώστε η πλευρά ΒΓ να είναι οριζόντια. Με τη δράση μιας ώθησης παράλληλης προς την ΒΓ σπρώχνουμε το τριγωνάκι ώστε να ξεκινήσει να στρέφεται με γωνιακή ταχύτητα ω.

Πόση πρέπει να είναι η τιμή της ω ώστε να στραφεί κατά 900, έτσι ώστε κατά τη στιγμή που θα φθάσει στο ανώτερο ύψος,

με μηδενική γωνιακή ταχύτητα,  η πλευρά ΒΓ να είναι κατακόρυφη.

 ( στη Βάσω Σπηλιοπούλου )

 

10. Η απερίγραπτη κίνηση της ράβδου. ˜˜˜˜

Μια ομογενής ράβδος έχει μάζα 200 g, μήκος 30 cm  και αρχικώς ακινητεί σε λείο οριζόντιο τραπέζι. Σε κάποια στιγμή χτυπιέται κάθετα από μία οριζόντια δύναμη σε σημείο που απέχει 10 cm από το μέσον της και της μεταβιβάζεται ορμή 3 Ns. Να περιγράψετε την κίνηση που θα επακολουθήσει.

( στον Παύλο Τζαμαλή )

 

11. Μετρώντας ενέργεια με ζυγό και με μεζούρα  ˜˜˜

Ένας ομογενής επίπεδος δίσκος ακτίνας R διατηρείται κατακόρυφος στρεφόμενος γύρω από ακλόνητο οριζόντιο άξονα που περνάει από το κέντρο του. Ένα κομματάκι μάζας m – θεωρούμενο  σημειακό αντικείμενο-  αποσπάται από την άκρη του δίσκου σε μια τέτοια στιγμή και σε μια τέτοια θέση ώστε στη συνέχεια - μετά δηλαδή την εκτόξευσή του- να κινηθεί κατακόρυφα προς τα πάνω στην κατακόρυφο του σημείου από το οποίο κόπηκε. Το μάζας m αυτό κομματάκι φθάνει σε ύψος Η και αρχίζει να πέφτει. Μετράμε με τη μετροταινία το ύψος Η και την ακτίνα του δίσκου και με ζυγό τη μάζα Μ του δίσκου και τη μάζα m του κομματιού που αποσπάστηκε. Βασιζόμενοι στις μετρήσεις και σε φυσικούς νόμους  υπολογίζουμε την κινητική ενέργεια του δίσκου πριν και μετά την  απόσπαση. Πώς το καταφέρνουμε; Το κομματάκι που αποσπάστηκε θεωρείται σημειακό αντικείμενο.

 ( στον Λάμπρο Ασημακόπουλο )

 

12. Μπιλιάρδο. Το χτύπημα με τη στέκα  ˜˜˜˜

Μια μπίλια του μπιλιάρδου ακτίνας R δέχεται απότομη ώθηση από μία οριζόντια στέκα σε απόσταση d πάνω από τον οριζόντιο άξονα x  που περνάει από το κέντρο μάζας. Η μπίλια φεύγει από τη στέκα με αρχική ταχύτητα υ0 αλλά λόγω του ότι το χτύπημα έγινε από ψηλά αποκτά ταχύτητα 9υ0/7. Να αποδείξετε ότι d = 4R/5

Αν η δύναμη ασκηθεί κάτω από τον άξονα x να αποδείξετε ότι είναι αδύνατον να δώσουμε στη μπίλια μία ταχύτητα προς τα πίσω εκτός εάν η ασκούμενη δύναμη  έχει κατακόρυφη συνιστώσα προς τα κάτω.

( στον Τάσο Καραμήτσο )

 

13. Ο σωλήνας μπορεί και να ανατραπεί;  ˜˜˜˜

Καθεμιά από τις δύο όμοιες ομογενείς σφαίρες έχει μάζα m  και ακτίνα  r. Ο ομογενής κυλινδρικός σωλήνας μέσα στον οποίο βρίσκονται ανοικτός και από τα δύο άκρα έχει μάζα Μ και ακτίνα R . Το σύστημα βρίσκεται σε οριζόντιο επίπεδο.   Να υπολογίσετε τον λόγο των μαζών m/M  ώστε ο κυλινδρικός σωλήνας με τις δύο σφαίρες να  ανατραπεί. Δίνεται R= 7r/4

 

 

( στην Αντιγόνη Κρασανάκη )

 

14.   Η πιο μεγάλη γωνία ˜˜˜˜

H ομογενής ράβδος, μήκους L,     ισορροπεί στον κατακόρυφο τοίχο και στο έδαφος.

Ποια είναι η μεγαλύτερη γωνία φ με το οριζόντιο έδαφος για την οποία ισορροπεί;

α. Στην περίπτωση που στον τοίχο η τριβή είναι αμελητέα και στην επαφή ράβδου εδάφους ο συντελεστής στατικής τριβής είναι  0,5.  ˜˜

β. Στην περίπτωση που και στα δύο σημεία στήριξης ο συντελεστής στατικής τριβής είναι  0,5. ˜˜˜˜

( στην Κική Λιανού )

 

15. Φρένο με δύο τριβές.  ˜˜˜

Ένας ομογενής κύλινδρος στρέφεται με γωνιακή ταχύτητα ω0 τοποθετείται έτσι ώστε να βρίσκεται σε επαφή και με το κατακόρυφο τοίχωμα και με την οριζόντια επιφάνεια.

Να προβλέψετε πότε θα σταματήσει εάν είναι γνωστή η ακτίνα του και η τιμή μ του συντελεστή τριβής, ίδια και για τις δύο επαφές του. 

 

 

 

 

( στον Θανάση Γεράγγελο )

 

16. Το βλήμα  και η ξύλινη σφαίρα.  ˜˜˜       

Ένα βλήμα μάζας m κινούμενο με οριζόντια ταχύτητα υ0 στο ενσφηνώνεται σε αρχικά ακίνητη ξύλινη σφαίρα  μάζας Μ και ακτίνας R η οποία ισορροπεί σε οριζόντιο επίπεδο. Η ταχύτητα του βλήματος πριν την ενσφήνωση βρίσκεται στο κατακόρυφο επίπεδο που περνάει από το κέντρο της σφαίρας και η  ενσφήνωση γίνεται σε ύψος h = ½R από το έδαφος.  Να προσδιορίσετε τα βασικά στοιχεία της κίνησης της σφαίρας με το ενσωματωμένο βλήμα μετά την ενσφήνωση.  Οι τριβές θεωρούνται αμελητέες. 

Να θεωρήσετε ότι η μάζα του βλήματος , συγκρινόμενη με τη μάζα της σφαίρας, είναι αμελητέα και ότι το βλήμα είναι  σημειακό αντικείμενο.   

 

 

( στη Μαριάνθη Βαρβαρούση )

 

17. Το μισό καρπούζι               ˜˜˜˜˜

Το σφαιρικό καρπούζι έχει κοπεί στη μέση. Το μισό  βρίσκεται σε οριζόντιο τραπέζι με το διαμετρικό του «κόκκινο» επίπεδο κατακόρυφο. Το αντικείμενο αφήνεται ελεύθερο και αρχίζει να πέφτει κυλιόμενο

 

χωρίς να ολισθαίνει προς τα δεξιά. Να υπολογίσετε τη δύναμη που ασκεί το καρπούζι στο τραπέζι κατά τη στιγμή που το διαμετρικό του επίπεδο (που έχει χρώμα κόκκινο ) γίνεται οριζόντιο.

Το αντικείμενο (μισό καρπούζι)  να θεωρηθεί ημισφαίριο μάζας m και ακτίνας R η ροπή αδράνειας του οποίου ως προς άξονα διερχόμενο από  το διαμετρικό επίπεδο και από το κέντρο του κύκλου Ο είναι 2mR2/5. Το κέντρο μάζας του ημισφαιρίου βρίσκεται στον άξονα συμμετρίας σε απόσταση 3R/8 από το διαμετρικό επίπεδο. Όταν το διαμετρικό επίπεδο γίνεται οριζόντιο η ακτίνα της τροχιάς του κέντρου μάζας να θεωρηθεί ίση με r.

 ( στον Ναπολέοντα Παπαδόπουλο )

 

 18. Η ανατροπή και η ανατροπή.      ˜˜˜˜   

Ένας συμπαγής και ομογενής κύλινδρος μάζας m  έχει ύψος Η, ακτίνα  βάσης R και βρίσκεται αρχικώς ακίνητος σε οριζόντιο τραπέζι χωρίς τριβή. Σε ύψος h από τη βάση του προσδένεται οριζόντιο νήμα το άλλο άκρο του οποίου συνδέεται μέσω τροχαλίας με ένα βαρίδι  Μ = 4m. Για ποιες τιμές του h ο κύλινδρος δεν ανατρέπεται και κινείται μεταφορικά; Η τροχαλία και το νήμα έχουν αμελητέες μάζες

 

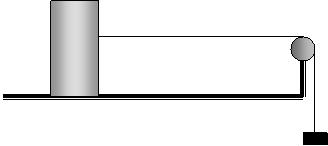
( στην Εύη Αβραμίδου )

 

19. Μέτρηση του συντελεστή τριβής με υποδεκάμετρο. ˜˜˜˜

Ένα ομογενές κουτί ακινητεί σε οριζόντιο τραπέζι. Χρησιμοποιώντας υποδεκάμετρο μετράμε το ύψος του - 30 cm - και την πλευρά της τετραγωνική βάσης. Την οποία βρίσκουμε 16 cm . Δοκιμάζουμε να το σπρώξουμε με μια οριζόντια δύναμη. Διαπιστώνουμε όπως ήταν αναμενόμενο ότι εάν το σπρώξουμε «χαμηλά» μπορούμε να το κάνουμε να κινηθεί μεταφορικά πάνω στο τραπέζι, ενώ εάν το σπρώξουμε σε σημείο που βρίσκεται «ψηλά» το κουτί ανατρέπεται. Με το υποδεκάμετρο προσδιορίζουμε ότι το σημείο πάνω από το οποίο το κουτί ανατρέπεται βρίσκεται σε ύψος 20 cm. Να υπολογίσετε τον συντελεστή στατικής τριβής. 

( στον Κώστα Στεφανίδη )

 

20. Αν το βαρίδι είναι αρκετά βαρύ.      ˜˜˜˜

Ένα αντικείμενο σαν λεκάνη βρίσκεται σε οριζόντιο τραπέζι και έχει μια σφαιρική κοιλότητα ακτίνας R και βάθους h και ακτίνας R. Μέσα στη σφαιρική αυτή κοιλότητα τοποθετούμε μία ομογενή σφαίρα ακτίνας R και μάζας m . Το αντικείμενο – λεκάνη έχει μάζα Μ και συνδέεται με νήμα μέσω τροχαλίας με ένα μικρό βαρίδι .

 

Σας ζητούμε βασιζόμενοι σε φυσικούς νόμους να προβλέψετε την τιμή της ελάχιστης μάζας που πρέπει να έχει το βαρίδι ώστε η σφαίρα να εξέλθει από την κοιλότητα.

( στον Νικήτα Μενούνο )

 

21.Ο πίθηκος είναι νηστικός                  ˜˜˜˜˜

Ένα σκοινί περνάει από μία ακίνητη τροχαλία και στο ένα του άκρο του είναι δεμένο ένα τσαμπί με μπανάνες και στο άλλο είναι γαντζωμένος ένας πεινασμένος πίθηκος χαμηλότερα από τις μπανάνες. Το τσαμπί με τις μπανάνες έχει το ίδιο βάρος με εκείνο του πιθήκου. Αρχικώς το σύστημα ακινητεί.  Ο πίθηκος αρχίζει να σκαρφαλώνει στο σκοινί προσπαθώντας να φθάσει στο ίδιο ύψος με τις μπανάνες.  Η διάμετρος της τροχαλίας είναι τόση ώστε εάν φθάσει στο ίδιο ύψος με τις μπανάνες, απλώνοντας το χέρι, θα μπορέσει να τις πιάσει. Θα τα καταφέρει; Θεωρούμε ότι η μάζα τόσο του σκοινιού όσο και της τροχαλίας είναι αμελητέα.

(στον Κώστα Σκορδούλη )

 

22. Το δακτυλίδι καθυστερεί.                    ˜˜

Ένας κύλινδρος και ένας δακτύλιος ίσων ακτίνων βρίσκονται σε επαφή σε κεκλιμένο επίπεδο γωνίας θ και συγκρατούνται. Τα δύο σώματα αφήνονται ταυτόχρονα και κυλίονται στην επιφάνεια του κεκλιμένου επιπέδου χωρίς να ολισθαίνουν. Πόσο θα απέχουν τα δύο κέντρα μάζας των δύο σωμάτων μετά από ένα δευτερόλεπτο; Τα σώματα είναι ομογενή.       Απ: 41,7 c m.

( στον Λουκά Κορφιάτη )

 

23. Ο τροχός στο πεζοδρόμιο.        ˜˜˜˜

Πόση ταχύτητα πρέπει να έχει το κέντρο μάζας του κυλιόμενου χωρίς ολίσθηση τροχού ώστε να ανέβει στο πεζοδρόμιο; Η ακτίνα του τροχού είναι 28 cm και το ύψος του ρείθρου 8 cm.

Πόση πρέπει να είναι η αντίστοιχη ταχύτητα ενός κύβου – σε μεταφορική κίνηση -  πλευράς ίσης με τη διάμετρο του τροχού ώστε να ανέβει το ίδιο πεζοδρόμιο; (Σε αυτή την περίπτωση θεωρούμε ότι στο 

σημείο που θα προσκρούσει ο κύβος υπάρχει ακμή όπως στο σχήμα )

( στον Παναγιώτη Καραμουσαντά )

 

24. Κι αν αργήσουμε να κόψουμε το νήμα;  ˜˜˜˜

Το ομογενές κιβώτιο μάζας m με τετραγωνική βάση πλευράς b = 26 cm, έχει ύψος Η = 70 cm,  συνδέεται με σπάγκο, μέσα από τροχαλία, με ένα βαρίδι η μάζα του οποίου είναι m/2. Το νήμα προσδένεται στο κιβώτιο σε ύψος 24 cm από την επιφάνεια του τραπεζιού. Αρχικά συγκρατούμε το κιβώτιο ώστε το σύστημα να ακινητεί και

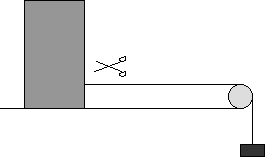
σε κάποια  χρονική στιγμή t= 0 το αφήνουμε ελεύθερο. Να προβλέψετε τι θα συμβεί σε καθεμιά από τις τρεις περιπτώσεις:

α. ο συντελεστής τριβής είναι 0,7

β. Ο συντελεστής τριβής είναι 0,4 και κόψουμε το νήμα τη χρονική στιγμή 0,1 s

γ. Ο συντελεστής τριβής είναι 0,4 και κόψουμε το νήμα τη χρονική στιγμή 1 s

Το κιβώτιο έχει σχήμα ορθογωνίου παραλληλεπιπέδου και η ροπή αδράνειας ως προς άξονα κάθετο στο επίπεδο του σχήματος που περνάει από το κέντρο μάζας είναι ίση με 1/12 ( Η2 + b2 ). Ο συντελεστής στατικής τριβής είναι ίσος με τον συντελεστή τριβής ολίσθησης . Τόσο η μάζα της τροχαλίας όσο και η μάζα του νήματος θεωρούνται αμελητέες.

( στον Κώστα Καλλέργη )

 

25. Ο Ηρακλής και το ρόπαλο         ˜˜˜˜

Ο Ηρακλής παίζει με το ρόπαλο. Επιχειρεί να το ισορροπήσει με το ένα δάκτυλο έτσι ώστε να το διατηρεί κατακόρυφο. Πώς είναι πιο εύκολο να το πετύχει;

Με το χοντρό μέρος να βρίσκεται προς τα πάνω ή με το χοντρό μέρος να είναι προς τα κάτω;

Η ΕΜΠΕΙΡΙΑ του λέει να κάνει το πρώτο αλλά 

η ΙΔΕΑ ότι «εάν το κέντρο βάρους είναι ΧΑΜΗΛΑ η ισορροπία θα είναι καλύτερη» του λέει να κάνει το πρώτο. Τι πρέπει να κάνει; Να εμπιστευτεί την εμπειρική του γνώση ή να υιοθετήσει την ιδέα;

Ρωτήσαμε ένα φυσικό πως θα μπορούσαμε να το ερευνήσουμε βασιζόμενοι στη  Φυσική και μας συμβούλευσε να επινοήσουμε ένα μοντέλο με γεωμετρική λογική στο οποίο να εφαρμόσουμε τους φυσικούς νόμους. Φανταστήκαμε λοιπόν μία μονοδιάστατη ράβδο αμελητέας μάζας  

και σε κάποιο σημείο της προσαρμοσμένο ένα σημειακό αντικείμενο μάζας m σε απόσταση d από τη βάση μεγαλύτερη από το μισό του μήκους της. Και την φανταστήκαμε αρχικά να ισορροπεί κατακόρυφα με το χέρι μας στη βάση της και στη συνέχεια να εκτρέπεται από την κατακόρυφο κατά γωνία φ. Ένας τρόπος να κρίνουμε το κατά πόσο είναι εύκολο να ανατραπεί είναι να υπολογίσουμε τη ΓΩΝΙΑΚΗ ΕΠΙΤΑΧΥΝΣΗ σε στιγμή που έχει εκτραπεί κατά γωνία φ για να διαπιστώσουμε έτσι ότι η βασιζόμενη στην ΕΜΠΕΙΡΙΑ υποψία μας είναι βάσιμη. Πώς θα το καταφέρουμε;

Το πρόβλημα γίνεται λίγο πιο δύσκολο εάν χρησιμοποιήσουμε ομογενή ράβδο μάζας Μ.

( στη Λία Χαλκιά )

 

 

26. Η άσπρη κιμωλία και η κόκκινη κιμωλία  ˜˜˜

Δύο κιμωλίες όμοιες πάνω σε θρανίο για το οποίο έχουμε μεριμνήσει ώστε να είναι κεκλιμένο επίπεδο γωνίας θ. Τη μία κιμωλία, την κόκκινη,  τη συγκρατούμε έτσι ώστε ο άξονας της να είναι παράλληλος 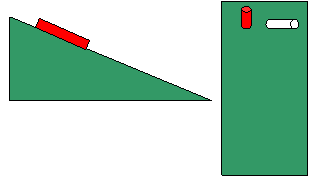προς το κεκλιμένο και να σχηματίζει με τον ορίζοντα γωνία θ.  Αν την αφήσουμε ελεύθερη θα ολισθήσει σε μεταφορική κίνηση. Η  άσπρη κιμωλία συγκρατείται στο χαμηλότερο σημείο της κόκκινης με τον άξονά της κάθετο στον άξονα της πρώτης και αν την αφήσουμε θα κυλήσει χωρίς ολίσθηση. Εάν τις αφήσουμε ταυτόχρονα μπορούμε, βάσει φυσικών νόμων, να προβλέψουμε ότι η άσπρη θα φθάσει πρώτη κάτω;

Μπορούμε επίσης να αποδείξουμε ότι

α. για να συμβεί η  ΜΕΤΑΦΟΡΙΚΗ ΚΙΝΗΣΗ της κόκκινης πρέπει να ισχύει μ < εφθ        

β. για να συμβεί η  ΚΥΛΙΣΗ ΧΩΡΙΣ ΟΛΙΣΘΗΣΗ της άσπρης πρέπει να  ισχύει μσ > εφθ/3 και

γ. εφόσον μ >εφθ/3  η κυλιόμενη λευκή θα φθάσει πρώτη κάτω.

Το μσ παριστάνει τον συντελεστή στατικής τριβής και το μ τον συντελεστή τριβής ολίσθησης

( στον Παντελή Λαρεντζάκη )

 

27. Κάθε σημείο και διαφορετική ταχύτητα   ˜˜˜˜

Πιάνουμε με το χέρι ένα τετράγωνο χαρτόνι ΑΒΓΔ  και το εκτοξεύουμε πάνω στο τραπέζι. Η κίνηση που κάνει δεν είναι μεταφορική. Σέρνεται πάνω στο τραπέζι και στρίβει ταυτόχρονα. Αν ξέρουμε ότι σε κάποια χρονική στιγμή η ταχύτητα   του σημείου Α έχει  μέτρο υ και κατεύθυνση προς το κέντρο του τετραγώνου  και ότι η διεύθυνση της ταχύτητας του Γ είναι κατά την ευθεία ΓΒ μπορούμε να προσδιορίσουμε τις ταχύτητες των Β, Δ και Γ. Πώς θα γίνει αυτό;

( στον Πέτρο Μιχαλακάκο )

 

28. Τα μυρμήγκια μετακινούν το ξυλαράκι   ˜˜˜˜

Σε εντυπωσιακή συνεργασία τα μυρμήγκια μετακινούν το ξυλαράκι ΖΗ. Πρόκειται για μια τυχαία κίνηση.

 Το άκρο Ζ έχει ταχύτητα μέτρου υ το διάνυσμα 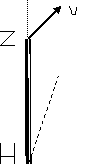    της οποίας σχηματίζει γωνία φ με τον άξονα ΖΗ. Το άκρο Η έχει ταχύτητα άγνωστου μέτρου η διεύθυνση της οποίας σχηματίζει γωνία θ με την ευθεία ΖΗ. Πώς μπορούμε να υπολογίσουμε το μέτρο της ταχύτητας του άκρου Η;  ( από το περιοδικό QUANTUM)

( στην Πανδώρα Χατζηδάκη )

 

 

29. Το βλήμα σε μεταφορική και στροφική κίνηση  ˜˜˜

Το βλήμα έχει μάζα m και κατευθύνεται προς τον στόχο του έχοντας και στροφική κίνηση περί τον άξονά του. Σε κάθε πλήρη περιστροφή το κέντρο μάζας του μετακινείται κατά 84π cm. Να υπολογίσετε πόσες φορές μεγαλύτερη είναι η κινητική του ενέργεια λόγω μεταφοράς από την κινητική ενέργεια λόγω περιστροφής. Η ροπή αδράνειας του βλήματος είναι ίση με τη ροπή αδράνειας ενός δακτυλίου μάζας m και ακτίνας 12 cm. (Απάντηση :  50 φορές μεγαλύτερη )

( στον Γιώργο Μωραΐτη )

 

30. Η σανίδα και οι κύλινδροι          ˜˜˜

Η πρισματική σανίδα έχει μάζα m,  βρίσκεται πάνω σε δύο κυλίνδρους και σύρεται σε μεταφορική κίνηση με οριζόντια δύναμη F ίση με το ¼ του βάρους της. Οι δύο κύλινδροι - καθένας τους μάζας ½m -κυλίονται χωρίς ολίσθηση σε οριζόντιο έδαφος, Να προσδιορίσετε την επιτάχυνση της σανίδας.

(Απάντηση :  2g/11)

( στον Βασίλη Δικαιουλάκο )

 

31. Το μπαλάκι του πινγκ πονγκ

Κρατάει στα χέρια της ένα μπαλάκι του πινγκ πονγκ. Σε κάποια στιγμή το εκτοξεύει προσεκτικά κατακόρυφα προς τα πάνω. Το μπαλάκι ανεβαίνει φθάνει στο ψηλότερο σημείο της τροχιάς και κατεβαίνει. Καμία έκπληξη. Αναρωτιέται εάν βασιζόμενη στη Φυσική θα μπορούσε να συγκρίνει το χρονικό διάστημα της ανόδου με το χρονικό διάστημα της καθόδου. Ξέρει ότι εάν μπορούσε να αγνοήσει την αντίσταση του αέρα τα δύο χρονικά διαστήματα θα ήταν ίσα, όπως συμβαίνει εάν η δοκιμή γίνει στο κενό ή όπως περίπου συμβαίνει εάν το αντικείμενο ήταν σιδερένιο. Τώρα όμως; Τι συμβαίνει με το μπαλάκι του πινγκ πονγκ; Τι την συμβουλεύετε; Πώς μπορεί να βασιστεί στη Φυσική και να δώσει μια απάντηση;          

 

 ( στον Γιάννη Φιορεντίνο )

 

32. Το αυγό είναι βρασμένο άραγε;     ˜˜˜˜

Δύο αυγά στο τραπέζι. Το ένα είναι βρασμένο σφικτό. Έχει όμως κρυώσει και δεν μπορούμε να το ξεχωρίσουμε με την αφή  από  το άλλο το άβραστο.  Οι παλιοί ξέρουν το «κόλπο». Στριφογυρίζουν και το ένα και το άλλο πάνω στο τραπέζι.  Εκείνο που στριφογυρίζει πιο εύκολα και  αργεί περισσότερο από το άλλο να σταματήσει είναι το σφιχτοβρασμένο. Για μια ακόμα φορά η ΕΜΠΕΙΡΙΚΗ ΓΝΩΣΗ θριαμβεύει. Τι λένε γι αυτό οι φυσικοί;

( στον Βασίλη Τσελφέ )

 

33. Οι ποδηλάτισσες    ˜˜˜

Ευρείς λεωφόρους διασχίζουν

φευγαλέα οι ποδηλάτισσες

Οδυσσέας Ελύτης

         Το ομώνυμο μυθιστόρημα της Ρέας Σταθοπούλου αρχίζει με τον στίχο του Οδυσσέα Ελύτη για τις ποδηλάτισσες. Όσο για μας τους γένους αρσενικού είναι γεγονός ότι το «μαγικό» αυτό δίτροχο του εφηβικού μας σύμπαντος  μάς προκαλούσε δέος. Όταν δεν έτρεχε έπεφτε και δεν έπεφτε μόνο όταν το κέντρο μάζας του είχε μια  ταχύτητα αξιοπρεπή. Ανεξήγητο για όποιον δεν έχει  συναντηθεί με τη Φυσική ή ξέρει μόνο από Μηχανική του υλικού σημείου. Δύο είναι οι βασικές  έννοιες με τις οποίες χρειάζεται να είναι εξοικειωμένος,  η στροφορμή και η ροπή και οι δύο μεγέθη διανυσματικά πράγμα που σημαίνει ότι για να κατανοήσει κανείς τις παραξενιές του ποδηλάτου πρέπει να διαθέτει και κάποια χωρική νοημοσύνη,   spatial intelligence όπως τη  λέει  ο Gardner. Η μεταβολή της στροφορμής ( ως προς κάποιο σημείο ) είναι ίση με την ώθηση της συνολικής ροπής (ως προς το ίδιο σημείο) μας λέει η Μηχανική του rigid body.

Αν φανταστούμε ένα τροχό ποδηλάτου ακίνητο με τον άξονά της περιστροφής του οριζόντιο. Αν ασκήσουμε μια δύναμη στον άξονα θα τον δούμε να στρέφεται απολύτως αναμενόμενα. Αν όμως έχουμε θέσει σε περιστροφή τον τροχό ΜΕ ΤΟΝ ΑΞΟΝΑ ΟΡΙΖΟΝΤΙΟ και ασκήσουμε στον άξονα μια δύναμη ΚΑΤΑΚΟΡΥΦΗ αυτό που θα συμβεί θα μας εντυπωσιάσει. Ο άξονας του τροχού ΘΑ ΣΤΡΑΦΕΙ ΣΕ ΟΡΙΖΟΝΤΙΟ ΕΠΙΠΕΔΟ. Και οι φυσικοί το αιτιολογούν με βάση τις γεωμετρικές ιδιαιτερότητες της

 

 

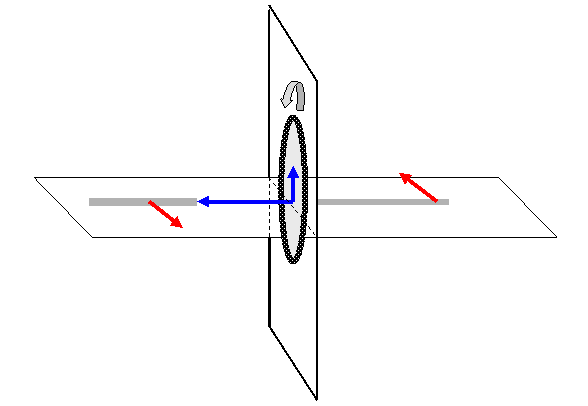
ροπής. Πώς ακριβώς;

Εφόσον το ποδήλατο είναι ακίνητο και το αφήσουμε θα ανατραπεί. Η ροπή του βάρους  λένε οι φυσικοί. Εάν όμως βρίσκεται σε κίνηση έχει ήδη στροφορμή και -εφόσον γύρει- η ροπή του «κατακόρυφου»

βάρους προσθέτει οριζόντια στροφορμή στην ήδη υπάρχουσα.

Πώς θα μπορούσαμε να κάνουμε ένα σχήμα και να τα παραστήσουμε  όλα αυτά την οριζόντια δηλαδή στροφορμή του τροχού κάθετα στην κίνηση και την οριζόντια -κατά τη διεύθυνση της κίνησης- στροφορμή η οποία προστίθεται διανυσματικά στην αρχική

( στη Ρέα Σταθοπούλου Παλαιοπούλου )

 

 

34. Από ξύλο και από χάλυβα          ˜˜˜

Ο χάρακας είναι ο μισός ξύλινος και ο μισός χαλύβδινος. Στην πρώτη δοκιμή στερεώνεται με το χαλύβδινο άκρο του σε άρθρωση και έτσι ώστε να μπορεί να στραφεί σε κατακόρυφο επίπεδο ενώ στο ξύλινο άκρο του ασκείται κατακόρυφη δύναμη προς τα πάνω και αποκτά γωνιακή ταχύτητα ω1 . Στη δεύτερη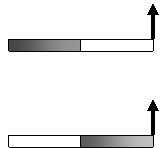δοκιμή ο χάρακας αναστρέφεται και στηρίζεται στην ίδια άρθρωση με το ξύλινο άκρο του, ασκείται η ίδια δύναμη στο άλλο του άκρο και η γωνιακή ταχύτητα είναι ω2. Να συγκρίνετε τις τιμές των ω1 και ω2  . Ο χάρακας να θεωρηθεί μονοδιάστατη ράβδος και καθένα από τα δύο του κομμάτια ομογενές.

( στον Θανάση Χριστοφιλόπουλο )

 

35. Το γεωμετρικό σημείο «κέντρο μάζας»       ˜˜

Θεωρούμε ένα σύστημα δύο κινουμένων υλικών σημείων σε πεδίο βαρύτητας έντασης g . Η μάζα m του συστήματος είναι ίση με το άθροισμα των μαζών των υλικών σημείων. Το κέντρο μάζας του συστήματος είναι ένα ΓΕΩΜΕΤΡΙΚΟ ΣΗΜΕΙΟ το οποίο σε κάθε στιγμή έχει μία θέση και μια ταχύτητα υcm. 

Με ποια από τα παρακάτω συμφωνείτε; 

α. Η ορμή του συστήματος είναι ίση με την ορμή ενός υλικού σημείου με μάζα ίση με τη μάζα m του συστήματος και ταχύτητα ίση με την ταχύτητα του κέντρου μάζας. p = mυcm.  

β. Η κινητική ενέργεια του συστήματος είναι ίση με την κινητική ενέργεια που θα είχε ένα υλικό σημείο μάζας ίσης με τη συνολική μάζα m του συστήματος ταχύτητα ίση με την ταχύτητα του κέντρου μάζας . 

K = ½mυcm2.

γ. Η – ως προς κάποια οριζόντια επιφάνεια – βαρυτική δυναμική ενέργεια του συστήματος των υλικών σημείων είναι ίση με τη δυναμική ενέργεια – ως προς την οριζόντια επιφάνεια - που θα είχε ένα υλικό σημείο μάζας  m που θα βρισκόταν στη θέση που βρίσκεται το κέντρο μάζας . U = mghcm.

( στη Τζένη Τσιτοπούλου )

 

36.Η σφήνα και το βαρίδι                        ˜˜˜˜˜

Η ομογενής ξύλινη σφήνα έχει μάζα Μ και μπορεί να ολισθαίνει πάνω σε  οριζόντια επιφάνεια. Στην κορυφή της βάζουμε ένα βαρίδι μάζας m και το αφήνουμε να γλιστρήσει στην κεκλιμένη πλευρά της. 

Η σφήνα κινείται με επιτάχυνση ασφ και το βαρίδι κατεβαίνει προς τη βάση με επιτάχυνση ως προς τη σφήνα α//.

Δίνεται το  ύψος  Η από το έδαφος στο οποίο αφήνεται το βαρίδι και η  γωνία φ της κεκλιμένης επιφάνειας με το οριζόντιο επίπεδο. Το βαρίδι θεωρείται σημειακό αντικείμενο και η  τριβή αμελητέα

 

 

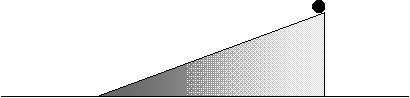
Αν οι μάζες των δύο αντικειμένων είναι ίσες να προσδιορίσετε.

α. τον λόγο α///ασφ                                                  ( Απ:   2/συνφ)

β. τις τιμές των α// και ασφ         

γ. την τροχιά του κέντρου μάζας του συστήματος

δ. την κινητική ενέργεια του συστήματος τη στιγμή που το βαρίδι φθάνει στη βάση

ε. το «πότε θα φθάσει» το βαρίδι στη βάση

στ. το «πού θα βρίσκεται» η σφήνα τη στιγμή που το βαρίδι φθάνει στη βάση

Να προσδιορίσετε όλα τα προηγούμενα στη γενική περίπτωση που ο λόγος Μ/m είναι λ.

( στον Βασίλη Γεωργουσόπουλο)

 

37. Γλιστράει στον τοίχο και στο πάτωμα. ˜˜˜˜

Η ομογενής ράβδος  ΑΒ , μήκους L,  βρίσκεται αρχικά ακίνητη σε κατακόρυφη θέση, πλάι στον τοίχο και αρχίζει να ολισθαίνει χωρίς τριβή έτσι ώστε να στηρίζεται 

γλιστρώντας τόσο στον τοίχο όσο και στο έδαφος. Σας ζητούμε:

α. Να προσδιορίσετε τη μορφή της τροχιάς του κέντρου μάζας

β. Να θεωρήσετε την κίνηση στροφική περί στιγμιαίο οριζόντιο άξονα περιστροφής διερχόμενο από σημείο Δ του κατακόρυφου επιπέδου και να προσδιορίσετε την τροχιά του σημείου Δ κατά την ολίσθηση της ράβδου.

γ. Να θεωρήσετε την κίνηση σύνθετη προερχόμενη από μία μεταφορική και από μία στροφική κίνηση περί άξονα που διέρχεται από το κέντρο μάζας και να προσδιορίσετε τόσο την ταχύτητα υΑστρ  του άκρου Α λόγω της στροφικής κίνησης όσο και την ταχύτητα υΑμετ του Α λόγω της μεταφορικής κίνησης σε χρονική στιγμή που η ολισθαίνουσα ράβδος  σχηματίζει με το έδαφος γωνία φ.

δ. Να προσδιορίσετε τις γωνίες που σχηματίζουν σε κάθε χρονική στιγμή της κίνησης οι ταχύτητες  υΑστρ και υΑμετ του Α  με την κατακόρυφο.

ε. Να συγκρίνετε την ταχύτητα του Α με την ταχύτητα του Β την ίδια χρονική στιγμή

στ. Να προσδιορίσετε τις ταχύτητες του κέντρου μάζας και των άκρων Α και Β τη στιγμή που η ράβδος σχηματίζει με το οριζόντιο έδαφος γωνία φ.                        

           [ υcm2 = 3gL(1-ημφ)/4 )          υΑ2 = 3gLσυν2φ( 1-ημφ)        υΒ2 = 3gLημ2φ( 1-ημφ)  ]

ζ. Να προσδιορίσετε την κεντρομόλο και την επιτρόχιο επιτάχυνση του κέντρου μάζας κατά τη στιγμή που η ολισθαίνουσα ράβδος  σχηματίζει με το έδαφος γωνία φ.

                  [ ακ,cm = 3g ( 1- ημφ ) / 2   αε,cm = 3g συνφ ) / 4  ]

η. Να προσδιορίσετε τις ταχύτητες του κέντρου μάζας και των σημείων Α και Β κατά   τη στιγμή που η ράβδος «προσγειώνεται» στο έδαφος και οριζοντιώνεται.

( στον Πάνο Μουρούζη )

 

38. Ο κύλινδρος μαζί και το στεφάνι   ˜˜˜

Ένας συμπαγής κύλινδρος συνδέεται αξονικά με ένα λεπτό στεφάνι  μέσω μιας αβαρούς ράβδου. Το σύστημα αφήνεται από ένα ύψος πάνω σε κεκλιμένη επιφάνεια γωνίας θ με το στεφάνι χαμηλότερα. Με δεδομένο ότι ο κύλινδρος και το στεφάνι έχουν το ίδιο βάρος Β και την ίδια ακτίνα σας ζητούμε να προσδιορίσετε:

α. τη δύναμη την οποία  ασκεί το στεφάνι  στην αβαρή ράβδο

β. την επιτάχυνση του κέντρου μάζας του κυλίνδρου

γ. την ταχύτητα του κέντρου μάζας του κυλίνδρου τη στιγμή που έχει μετακινηθεί κατά d από τη θέση που τον αφήσαμε. 

 

( στον Μαρίνη Πετρόπουλο )

 

 

39. Αγώνας δρόμου των δύο ισοβαρών ˜˜˜˜

 

Το σύστημα αφήνεται από μια θέση ελεύθερο από μια θέση έτσι ώστε το αβαρές νήμα να είναι τεντωμένο και οριζόντιο και η τροχαλία ακριβώς στο μέσο της απόστασης των δύο αντικειμένων. Τα δύο αντικείμενα έχουν ίσες μάζες και θεωρούνται σημειακά . Το Α κατευθύνεται προς την τροχαλία και το Β προς ένα σημείο της κατακόρυφης πλευράς του τραπεζιού. Ποιο θα φθάσει πρώτο στο σημείο που κατευθύνεται; ( από το περιοδικό QUANTUM)

( στον Αλέκο Μάμαλη )

 

39. Οι φυσικοί διαφωνούν στον πρασινοπίνακα ˜˜˜˜

Η μπίλια κυλίεται χωρίς ολίσθηση σε οριζόντια επιφάνεια. Το Α που είναι και το μοναδικό σημείο επαφής με την οριζόντια επιφάνεια έχει εξ ορισμού μηδενική ταχύτητα. Πως μπορούμε να προσδιορίσουμε την επιτάχυνση του σημείου Α;

Το συζητούν δύο φυσικοί. Λέει ο Σάββας : «Βασίλη το σημείο Α «έχει» επιτάχυνση.

Το αρνείται ο Βασίλης.  «Το μηδενικής ταχύτητας Α δεν έχει επιτάχυνση.  Κοίτα ρε Σάββα εάν θεωρήσουμε την κίνηση της μπίλιας  σύνθετη προερχόμενη  από σύνθεση μιας μεταφορικής με την επιτάχυνση του κέντρου μάζας και μιας στροφικής περί άξονα που διέρχεται από το κέντρο μάζας θα . . . . . . . .  πρέπει να κάνω ένα σχήμα . Παίρνει μια λευκή κιμωλία και κάνει ένα σχήμα  στον πίνακα. Χρησιμοποιεί και κόκκινη για τις επιταχύνσεις και

 

 

 

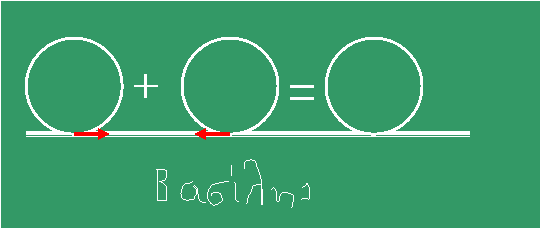
συνεχίζει «Λόγω της μεταφορική κίνησης η επιτάχυνση του Α είναι ίση με εκείνη του κέντρου μάζας και λόγω της στροφικής κίνησης η επιτάχυνση του ίδιου σημείου είναι αντίθετη. Κατά συνέπεια η ολική επιτάχυνση είναι μηδέν». 

Ο Σάββας όμως παρεμβαίνει « Ξέρεις κάτι, Βασίλη, ξέχασες ότι λόγω της στροφικής κίνησης το σημείο Α έχει και κεντρομόλο επιτάχυνση .» Παίρνει  κιμωλία μπλε χρώματος και συμπληρώνει στο σχήμα

«Και, τελικά,  η μπλε επιτάχυνση θα είναι η ολική επιτάχυνση  του σημείου Α».

Ο Βασίλης όμως δεν το βάζει κάτω « Μα η μπλε επιτάχυνση στην οποία καταλήγεις είναι κεντρομόλος επιτάχυνση και ΔΕΝ ΕΙΝΑΙ ΔΥΝΑΤΟΝ ΕΝΑ ΣΗΜΕΙΟ ΜΗΔΕΝΙΚΗΣ ΤΑΧΥΤΗΤΑΣ, όπως είναι το Α,  ΝΑ ΕΧΕΙ ΚΕΝΤΡΟΜΟΛΟ ΕΠΙΤΑΧΥΝΣΗ».

Ο Σάββας τον κοιτάζει σκεπτικός.   Ποιος νομίζετε ότι έχει δίκιο;

(στον Βαγγέλη Καραλή)

 

41. Θα μετακινηθεί ο θάλαμος;   ˜˜˜˜

Ο κλειστός θάλαμος είναι αρχικά ακίνητος σε οριζόντιο έδαφος . Ο συντελεστής στατικής τριβής μεταξύ της βάσης του θαλάμου και του οριζοντίου εδάφους είναι μσ . Μέσα στον θάλαμο βρίσκεται κάποιο λογικό πλάσμα που έχει κρεμάσει με σπάγκο,  από την οροφή ένα βαρίδι μάζας  m. Διατηρώντας το νήμα τεντωμένο μετακινεί το βαρίδι στο ψηλότερο σημείο του θαλάμου έτσι ώστε το νήμα να γίνει οριζόντιο και το αφήνει και το βαρίδι. 

  

Να υπολογίστε την ελάχιστη τιμή του συντελεστή στατικής τριβής μσ ώστε κατά την αιώρηση του εκκρεμούς ο θάλαμος να μη μετακινείται πάνω στο οριζόντιο έδαφος.

 Η συνολική μάζα θαλάμου και πλάσματος είναι Μ.

( στον Γιάννο Καρανίκα )

 

42. Εκείνος κυλιέται το κέντρο μάζας ταλαντώνεται   ˜˜˜

Σε έναν ομογενή και συμπαγή κύλινδρο μάζας 2 kg προσδένουμε κατάλληλα ένα οριζόντιο αβαρές ελατήριο σταθεράς 3 N/m έτσι ώστε να μπορεί να κυλίεται χωρίς να ολισθαίνει σε οριζόντια επιφάνεια. Διατηρώντας τον κύλινδρο πάνω στο οριζόντιο έδαφος τον μετακινούμε από τη θέση ισορροπίας κατά 25 cm και τον αφήνουμε ελεύθερο. Σας ζητούμε α. Να υπολογίσετε την κινητική ενέργεια λόγω μεταφορικής κίνησης καθώς και την κινητική ενέργεια λόγω περιστροφικής κίνησης του κυλίνδρου τη στιγμή που περνάει από τη θέση ισορροπίας   β. να αποδείξετε ότι το κέντρο μάζας του κυλίνδρου θα εκτελέσει αρμονική ταλάντωση περιόδου 2π s.

 

( στον Ζήση Σακκά )

 

43. Τα δυο μολύβια και οι μπίλιες που τις έλεγαν γκαζές ˜˜˜

Στα χρόνια της παιδικής μας αθωότητας κυκλοφορούσαν κάτι γυάλινες μπίλιες με χρώματα που τις έλεγαν γκαζές. Με ακτίνα κάπου πέντε με δέκα χιλιοστά δίδασκαν τα παιδιά των αθηναϊκών δρόμων το φαινόμενο «κύλιση χωρίς ολίσθηση» μέσα από εμπειρίες απόλαυσης. Αν βάλουμε μια τέτοια γυάλινη μπίλια πάνω σε δυο παρόμοια μολύβια που τα έχουμε  πάνω στο τραπέζι ακινητοποιημένα και παράλληλα έτσι ώστε η μπίλια να ακουμπάει στο τραπέζι θα διαπιστώσουμε ότι ισορροπεί. Αν όμως φροντίσουμε ώστε τα δύο ακινητοποιημένα μολύβια να μην είναι παράλληλα η μπίλια θα κυλήσει πάντα προς τη μεριά του «ανοίγματος» Και να το πούμε διαφορετικά. Μπορούμε εμπειρικά – μέσω της οδού Αριστοτέλους - να διαπιστώσουμε την «πλατωνική» παραλληλία των αξόνων των δύο  μολυβιών. Φτάνει η μπίλια να μην κυλάει. Τι λέει γι αυτό η Φυσική;

Βάλαμε μια τέτοια μπίλια 40 γραμμαρίων και ακτίνας 10 mm έτσι ώστε τα σημεία επαφής με τα δύο μολύβια να απέχουν 12 mm και την αφήσαμε να κυλήσει πάνω σε δύο όχι παράλληλα μολύβια. Όταν είχε φθάσει σε θέση τέτοια που τα δύο σημεία επαφής  απείχαν 16 mm σκεφτήκαμε ότι θα μπορούμε να υπολογίσουμε  την κινητική της ενέργεια και την ταχύτητα του κέντρου μάζας. Αφού τη ζυγίσαμε και υπολογίσαμε ότι η μάζα της είναι 40 g,  καταφύγαμε στη Γεωμετρία και στη Φυσική το καταφέραμε. Πώς το καταφέραμε;

Τέλος, εμπιστευόμενοι τη Γεωμετρία, αποδείξαμε ότι η τροχιά της προβολής του κέντρου μάζας ( πάνω στο τραπέζι ) σχημάτιζε με την τροχιά του κέντρου μάζας γωνία ίση με εκείνη την οποία σχημάτιζε με τον άξονα του ενός μολυβιού. Πώς το αποδείξαμε;

 

 

 

( στον Χρήστο Σιαμαντά )

 

44. Ο τροχος θα ανέβει πιο ψηλά από τη μπίλια;   ˜˜˜

Ο τροχός και η μπίλια ΄φθάνουν με την  ίδια ταχύτητα ( κέντρου μάζας ) στην ανηφοριά. Το στοίχημα είναι ποιος θα ανέβει πιο ψηλά. Τις προάλλες στο «ποιος θα κατέβει πιο γρήγορα στην κατηφόρα»

κέρδισε η μπίλια. Τι θα γίνει τώρα; Έχει ελπίδες ο τροχός ; 

( στη Ρούλα Χόρτη )

 

 

 

45. Η Michel Pfeiffer στην αίθουσα του μπόουλινγκ   ˜˜˜

Στο «Φράνκι και Τζόνι», στην αίθουσα του μπόουλινγκ, η Μισέλ Φάιφερ ως σερβιτόρα Frankie πιάνει  τη μπάλα και την πετάει με μεγάλη επιδεξιότητα προς τις κορίνες,  προσδίδοντάς της  οριζόντια ταχύτητα υ0. Η μπάλα ξεκινάει με «διαθέσεις» μεταφορικής κίνησης αλλά η παρουσία της τριβής την κάνει να εκτελεί «κύλιση με ολίσθηση» με την ταχύτητα του κέντρου μάζας συνεχώς να ελαττώνεται.  Όταν η ταχύτητα του κέντρου μάζας γίνεται 5 υ0/7 η μπάλα κυλίεται χωρίς ολίσθηση . 

Πώς μπορούμε να το αποδείξουμε;

( στην Ιωάννα Αδαμοπούλου )

 

46. Όταν έλιωσε ο πάγος           ˜˜˜˜

Πάνω σε ένα κυκλικό τραπέζι το οποίο στρέφεται περί κατακόρυφο άξονα με σταθερή γωνιακή ταχύτητα βρίσκεται ένα κυκλικό δοχείο το οποίο στρέφεται μαζί με το τραπέζι χωρίς τριβή και χωρίς εξωτερική ροπή. Ο πυθμένας του δοχείου καλύπτεται με ένα στρώμα πάγου  ομοιόμορφου  πάχους. Ο πάγος λιώνει χωρίς να χυθεί νερό από το δοχείο. Τι θα συμβεί με τη γωνιακή ταχύτητα;  Θα μεγαλώσει, θα μικρύνει ή δεν θα μεταβληθεί;

( στον Αριστοτέλη Γκιόλμα )

 

 47. Μπιλιάρδο, ακινητοποίηση και καθετότητα   ˜˜˜

Το τραπέζι του μπιλιάρδου και η μία μπίλια, η Β, «περιμένει» ακίνητη χωρίς να ξέρει ατό που θα της συμβεί. Ο παίκτης που  σημαδεύει με τη στέκα την άλλη μπίλια, την Α, ξέρει και μπιλιάρδο και Γεωμετρία και Φυσική. Ξέρει λοιπόν πως εάν η κρούση θεωρηθεί ελαστική – και η προϋπόθεση μπορεί να μην ισχύει απόλυτα αλλά δεν είναι σκανδαλώδης στο γήπεδο της Πραγματικότητας – η μοίρα της επιτιθέμενης μπίλιας Α θα την οδηγήσει σε δύο μόνο ενδεχόμενα. Ή θα κινηθεί κάθετα στην αρχική της κατεύθυνση ή θα ακινητοποιηθεί μεταβιβάζοντας όλη την ενέργειά της στην αρχικά ακίνητη. Εκείνος το έχει αποδείξει πριν δοκιμάσει το χτύπημα με τη στέκα, βασιζόμενος στη Διατήρηση της ενέργειας, στη Διατήρηση της ορμής και στη Γεωμετρία. Η καθετότητα θα προκληθεί εάν χτυπήσει λοξά ενώ η ακινητοποίηση της επιτιθέμενης εάν σημαδέψει  έτσι ώστε τη στιγμή της σύγκρουσης, η ταχύτητα του κέντρου μάζας να ανήκει στην 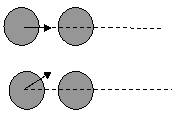ευθεία x΄x των δύο κέντρων μάζας. Κεντρική κρούση το λένε οι φυσικοί.

Έχει επίσης αποδείξει ότι, η εφόσον η κρούση είναι πλάγια, έτσι ώστε η οξεία γωνία της πριν από τη σύγκρουση ταχύτητας της επιτιθέμενης Α με την ευθεία x΄x να είναι θ, η κινητική ενέργεια που θα έχει μετά τη σύγκρουση θα είναι  Κσυν2θ,  όπου Κ η κινητική ενέργεια που είχε πριν από τη σύγκρουση. Αν μάλιστα η θ είναι γωνία 450, οι δύο μπίλιες θα μοιραστούν εξίσου τα τζάουλ της επιτιθέμενης.

  

( στη Λιάνα Τσαμπή )

 

48. Το κόλπο για να μη γλιστρήσει η σανίδα ˜˜˜˜

Η ομογενής σανίδα είναι 14 κιλά και τοποθετείται στα δύο σκαλοπάτια όπως στο σχήμα. Ανάμεσα σ’ αυτήν και στα σκαλοπάτια δεν υπάρχει τριβή και εξυπακούεται ότι αν την αφήσουμε θα γλιστρήσει. Βασιζόμενοι στους νόμους της Φυσικής μπορούμε να αποδείξουμε ότι εάν αντικείμενο 70 κιλών κινηθεί πάνω στη σανίδα με συγκεκριμένη σταθερή επιτάχυνση, όσο αυτό θα κινείται η σανίδα δεν θα γλιστράει. Πως υπολογίζεται αυτή η επιτάχυνση; Έχουμε μετρήσει ότι το ύψος κάθε σκαλοπατιού είναι 30 cm και το πλάτος 40 cm.   

( στον Τάσο Σινάνη )

 

49. Ο μεγάλος κύλινδρος πάνω από τον μικρό  ˜˜˜       

Δύο κύλινδροι ακτίνων αντίστοιχα 20cm και 125cm ακινητούν σε οριζόντια επιφάνεια εφαπτόμενοι. Στο ανώτερο σημείο του μεγάλου κυλίνδρου ασκείται μια οριζόντια δύναμη. Με δεδομένα ότι ο συντελεστής στατικής τριβής στην επαφή κάθε κυλίνδρου με το έδαφος είναι μ και ο συντελεστής στατικής τριβής στην επαφή των δύο κυλίνδρων είναι μ’  να προσδιορίσετε την αναγκαία συνθήκη ώστε ο μεγάλος κύλινδρος να περάσει πάνω από τον μικρό.

( στην Έφη Σιούτα )

 

50. Μέτρηση μιας γωνίας με ζυγό. ˜˜˜

Ο συμπαγής κύβος μάζας τον οποίο προηγουμένως ζυγίσαμε και βρήκαμε ότι το βάρος του είναι 4 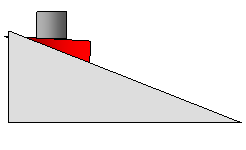νιούτον τον έχουμε τώρα βάλει σε ένα αβαρές  βάθρο το οποίο φέρει ζυγό με ελατήριο. Το σύστημα το αφήσαμε να γλιστρήσει σε κεκλιμένο επίπεδο χωρίς τριβή έτσι ώστε η πλατφόρμα του ζυγού να παραμένει διαρκώς οριζόντια. Διαπιστώσαμε ότι σε αυτού του είδους τη ζύγιση  ο ζυγός έδειξε  3 νιούτον. Πώς μπορούμε,  βασιζόμενοι στις δύο ζυγίσεις και στους νόμους της φυσικής,  να υπολογίσουμε τη γωνία του κεκλιμένου επιπέδου;  

( στον Κώστα Παντίδη )

 

 51. Η μπίλια στην πλατφόρμα ˜˜˜

Η πλατφόρμα κινείται με σταθερή ταχύτητα και το απολύτως λείο της δάπεδό της έχει σχήμα τετράγωνο πλευράς 6 m Στο κέντρο του τετραγώνου υπάρχει μια μικρή μπίλια η οποία ακινητεί ως προς το δάπεδο συμμετέχουσα της κίνησης της πλατφόρμας. Σε κάποια χρονική στιγμή η πλατφόρμα φρενάρει με σταθερή επιβραδύνουσα επιτάχυνση και η μπίλια κινούμενη χωρίς τριβή προσπίπτει κάθετα στο τοίχωμα της πλατφόρμας και ανακλάται. Στην επιστροφή μηδενίζεται γαι πρώτη φορά η σχετική της ταχύτητα όταν βρεθεί σε απόσταση 2,4 μέτρων από το τοίχωμα στο οποίο έγινε η πρόσπτωση. Σας  ζητούμε να υπολογίσετε το των κινητικών ενεργειών της μπίλιας πριν και μετά την πρόσκρουση. Η μπίλια θεωρείται σημειακό αντικείμενο.

( στον Γιάννη Γάτσιο )

 

52. Τόση ώστε να το σηκώσουμε  ˜˜˜˜

Το σώμα Σ2 έχει βάρος 3 Ν και βρίσκεται στο έδαφος ενώ το Σ1 έχει βάρος 7 Ν και  ισορροπεί πάνω στο παρεμβαλλόμενο κατακόρυφο ελατήριο. Πόση δύναμη πρέπει να ασκήσουμε κατακόρυφα προς τα κάτω στο Σ1 ώστε ε’αν στη συνέχεια αφήσουμε το σύστημα ελεύθερο να προκληθεί ανύψωση του Σ2 από το έδαφος; 

 

 

 

( στον Γιάννη Κατσικάρο )

 

53. Οι περιπέτειες των ευρώ     ˜˜˜˜˜      

Δύο ίδια κέρματα ευρώ είναι ακίνητα πάνω σε ένα τραπέζι χωρίς τριβή. Το σχήμα δείχνει σε κάτοψη το ορθογώνιο επίπεδο ΑΒΓΔ που παριστάνει την οριζόντια επιφάνεια του τραπεζίου και στην άκρη ΑΒ τα δύο κέρματα έτσι ώστε τα δύο κέντρα μάζας να ισαπέχουν από την πλευρά ΑΒ. Την ίδια χρονική στιγμή, την οποία θεωρούμε αρχή των χρόνων ασκείται σε καθένα από τα κέρματα μία δύναμη. Τα μέτρα των δύο δυνάμεων είναι ίσα και οι διευθύνσεις τους παράλληλες προς την πλευρά ΒΓ. Η ασκούμενη στο κέρμα 1  δύναμη F1 ασκείται συνεχώς στο σημείο Γ της περιφέρειας του κέρματος έτσι ώστε ο φορέας της να περνάει από το κέντρο μάζας. Η ασκούμενη στο κέρμα 2  δύναμη F2 ασκείται στο σημείο Δ της περιφέρειας του κέρματος έτσι ώστε κατά την αρχή των χρόνων να είναι εφαπτομένη  στην περιφέρεια. Κατά την διάρκεια των κινήσεων που ακολουθούν και οι δύο δυνάμεις είναι σταθερές και ασκούνται συνεχώς στο ίδιο σημείο του αντίστοιχου κέρματος.

α. Να συγκρίνετε τα δύο χρονικά διαστήματα της κίνησης του κάθε κέρματος από την αρχική τους θέση στην απέναντι πλευρά ΓΔ.

β. Να περιγράψετε την κίνηση κάθε κέρματος.

γ. Σε περιγράψετε την κίνηση που θα έκανε το κέρμα 2 σε περίπτωση που η ασκούμενη σε αυτό σταθερή δύναμη δεν δρούσε στο ίδιο σημείο του κέρματος αλλά δρούσε έτσι ώστε ο φορέας της να διατηρείται συνεχώς εφαπτόμενος στην περιφέρεια του κέρματος.   Τα κέρματα να θεωρηθούν ομογενείς δίσκοι.

( στον Δημήτρη Τσαούση, ή  «Μήτσο» όπως τον φωνάζει εδώ και χρόνια ο Ζήσης ο Σακκάς )

 

53. Το χαλί στη βεράντα ˜˜˜

Θέλει να ξεσκονίσει το μικρό χαλί και το έχει κρεμάσει στη βεράντα στο γείσο του μπαλκονιού έτσι ώστε να κατά ένα μέρος να κρέμεται προς τα έξω και κατά ένα μέρος προς το μέρος της βεράντας.

Διατηρώντας τις δύο άκρες οριζόντιες, το μετακινεί προσεκτικά ώστε να κρέμεται προς τα έξω όλο και περισσότερο. Το εγχείρημα έχει αρχίσει να γίνεται επικίνδυνο, διότι υπάρχει ενδεχόμενο να γλιστρήσει το χαλί και να πέσει από τον τρίτο όροφο. Αναρωτιέται πώς θα μπορούσε να επινοήσει ένα μοντέλο σαν αυτά που χρησιμοποιεί η Φυσική να προβλέψει το μέγιστο μήκος χαλιού που θα μπορούσε να κρέμεται χωρίς να πέφτει.

Το μήκος του χαλιού είναι 2 m,  το πάχος του γείσου της βεράντας 20 cm και ο συντελεστής τριβής 0,5.

( Στον Γιάννη Ρέντζο )

 

55. Στην αγκαλιά της παγκόσμιας έλξης   ˜˜˜        

Δύο σημειακά αντικείμενα, μαζών  M και m,  βρίσκονται σε πολύ μεγάλη απόσταση και η μόνη  ασκούμενη σε αυτά δύναμη είναι η μεταξύ τους δύναμη παγκόσμιας έλξης

Στην αρχή των χρόνων δεχόμαστε ότι τα αντικείμενα ακινητούν και στη συνέχεια προσεγγίζουν λόγω της παγκόσμιας έλξης. Να αποδείξετε ότι για τη σχετική ταχύτητα υσχ   με την οποία το ένα προσεγγίζει το άλλο ισχύει υ2σχ = 2G( M + m )/d, όπου d η μεταξύ τους απόσταση και G η σταθερά της παγκόσμιας έλξης

( στην Αριστέα Μπουλουξή)

 

56. Η πίστη στους νόμους Διατήρησης      ˜˜˜    

Ένας πλανήτης περιφέρεται γύρω από τον ήλιο του σε ελλειπτική τροχιά. Όπως δεχόμαστε ότι ισχύει για όλο το Σύμπαν,  ο ήλιος του ασκεί ελκτική δύναμη της μορφής F = k/a2, όπου α η απόσταση από το κέντρο του ήλιου. Όταν περνάει από το πιο μακρινό σημείο της τροχιάς ( το αφήλιο θα λέγαμε εάν επρόκειτο για τον πλανήτη Γη ) και απέχει α από το κέντρο του ήλιου για την ταχύτητά του υ ισχύει

υ2 = k/2ma. Βασιζόμενοι σε συγκεκριμένους νόμους Διατήρησης να υπολογίσετε την ταχύτητα του πλανήτη όταν βρεθεί στο κοντινότερο από τον ήλιο (του)  σημείο της τροχιάς. ( Απ. α/3 )

( στη Φάνη Στυλιανίδου )

 

57. Ανεβαίνει επειδή υπάρχει βαρύτητα;     ˜˜˜    

Ρώτησαν ένα  σοφό: « Γιατί ανεβαίνει ο φελλός όταν βάζουμε στο νερό ;» Κι εκείνος απάντησε: « Γιατί υπάρχει βαρύτητα . Γιατί ζούμε σε ένα πεδίο βαρύτητας». Τι εννοούσε; Μήπως ήταν κουρασμένος; 

( στον Παύλο Μίχα )

 

58. Ο υδράργυρος στο εκκρεμές ˜˜˜

Η περίοδος της ταλάντωσης κάθε φυσικού εκκρεμούς διαμορφώνεται και από την απόσταση από το σημείο ανάρτησης μέχρι το κέντρο μάζας

Σε ορισμένα παλιά ρολόγια τοποθετημένα σε ανοικτούς χώρους το εκκρεμές ήταν ένας μακρύς σωλήνας στο κάτω μέρος του οποίου υπήρχε ένα δοχείο με υδράργυρο. Σε τι εξυπηρετούσε άραγε;

( στη Μαρία Δεβελάκη )

 

59. Το ημερήσιο ταξίδι της σκιάς ˜˜˜

Αύγουστος στη Μήλο κι εκείνο το βράδυ με τα ούζα λέει σε κάποια στιγμή ο Κώστας Καμπούρης: «Διάβασα στο βιβλίο του James Cushing ότι εάν βάλεις ένα ραβδί στο έδαφος ώστε να διατηρείται κατακόρυφο, η άκρη της σκιάς θα διαγράψει έλλειψη. Τι λες γι αυτό;»

Το άλλο πρωί βρήκα ένα ραβδί ένα μέτρο περίπου, το στήριξα στο έδαφος της Μήλου και έφτιαξα το ηλιακό ρολόι. Όπως ήταν αναμενόμενο, καθώς κύλαγαν οι ώρες του πρωινού, η σκιά μίκραινε και στη συνέχεια άρχισε να μεγαλώνει, ενώ λίγο πριν από το ηλιοβασίλεμα έγινε πολύ μεγάλη και στη συνέχεια χάθηκε.

Είχα εν τω μεταξύ φροντίσει από νωρίς το πρωί να βρω μικρά λευκά βότσαλα και να βάζω, κάθε τόσο, ένα από αυτά στο σημείο που βρισκόταν το άκρο της σκιάς. Το βραδάκι μπορούσε κανείς να διακρίνει ότι τα βότσαλα έδειχναν να βρίσκονται πάνω σε τμήμα μιας ΕΛΛΕΙΨΗΣ. Πώς θα μπορούσαμε να δώσουμε μια εξήγηση στο φαινόμενο της δημιουργίας της έλλειψης;

( στον Κώστα Καμπούρη )

 

 

60. Τα κύματα της θάλασσας ˜˜˜

Στο Κόρθι της ’νδρου, απογεματάκι, κι εκείνος κάθεται και παρατηρεί τα κύματα καθώς έρχονται με φορά και σκάνε στην ακτή. Προσέχει ότι καθώς ένα μεγάλο κύμα πλησιάζει στα ρηχά, το νερό στην κορυφή του κύματος συστρέφεται και πέφτει. Αναρωτιέται «γιατί» να συμβαίνει αυτό. Σε τέτοιοι είδους «γιατί» η Φυσική συνήθως μπορεί και δίνει απαντήσεις. Τι γίνεται σε αυτή την περίπτωση; 

( στον Χρήστο Δούκα )

 

 

61. Μετρήσεις υπόγειες  ˜˜˜

Σε ένα μυθιστόρημα επιστημονικής φαντασίας οι δυο φυσικοί κατεβαίνουν με σταθερή ταχύτητα μέσα στον ίδιο θάλαμο και κατευθύνονται σε ένα ιδιαίτερα βαθύ ορυχείο. Ο ένας κρατάει ένα ζυγό με σταθμά με τον οποίο ζυγίζει  ένα αντικείμενο μάζας 500 γραμμαρίων. Ο άλλος έχει ένα δυναμόμετρο από το οποίο έχει κρεμάσει ένα όμοιο αντικείμενο μάζας επίσης 500 g.  Είναι ίδιες οι ενδείξεις των δύο οργάνων;

( στον Γιώργο Τουντουλίδη )

 

61. Δοκιμές υποθαλάσσιες  ˜˜˜

Δύο μεγάλου μήκους χάλκινοι σωλήνες βυθίστηκαν σε μεγάλο βάθος στον ωκεανό. Ο ένας είναι ερμητικά σφραγισμένος στα δύο άκρα του, ενώ ο άλλος έχει το ένα του άκρο ανοικτό. Τι θα συμβεί με τον κάθε σωλήνα;

( στον Γιώργο Κοντόκωστα )

 

62. Μέτρησε βάρος και μήκος με πιεσόμετρο  ˜˜˜

Είχε ένα σωρό όμοια τούβλα από μία οικοδομή. Έφτιαξε ένα πιεσόμετρο και διαπίστωσε ότι για ένα τούβλο που στηριζόταν στη μεγαλύτερη έδρα του η πίεση στη βάση του ήταν 1800 Pa. Όταν έβαλε το τούβλο να στηρίζεται στη μικρότερη έδρα η πίεση στη βάση ήταν 6000 Pa, ενώ όταν στηριζόταν στη ενδιάμεσων διαστάσεων έδρα του η πίεση στη βάση ήταν 3000 Pa. Έφτιαξε έναν τοίχο ύψους 3 μέτρων με παρόμοια τούβλα και διαπίστωσε ότι η πίεση στη βάση του τοίχου ήταν 90000 Pa. Με τις τέσσερις αυτές μετρήσεις υπολόγισε το βάρος και τις διαστάσεις κάθε τούβλου. Πώς το κατάφερε; 

( στον Φώτη Κολοβό )

 

63. Το καρφί, ο μαγνήτης και η κατάλληλη κίνηση ˜˜˜

Πάνω στο ένα τραπέζι ένας πεταλοειδής μαγνήτης και σε ορισμένη απόσταση ένα καρφί. Πώς πρέπει  να πλησιάσουμε τον μαγνήτη στο καρφί ώστε να «κολλήσουν» ταυτόχρονα το κεφάλι και η αιχμή του καρφιού στους πόλους του;

( στη Δήμητρα Θεοδωροπούλου Καραλή)

 


64. Η επιτάχυνση του γιωταχί  ˜˜˜

Το γιώτα χι είναι 1200 κιλά και κινείται σε οριζόντιο έδαφος με επιτάχυνση κέντρου μάζας 0,1 g. Εάν το ύψος του κέντρου βάρους είναι h, και φανταστούμε ως  Ε το κατακόρυφο επιπέδου στο οποίο ανήκει το κέντρο βάρους, η απόσταση κάθε μπροστινού τροχού από το Ε είναι d= 2,5 h και η απόσταση καθενός του σημείου στήριξης κάθε πίσω τροχού από το επίπεδο Ε είναι 1,02d.

 Να προσδιορίσετε την κατακόρυφη δύναμη που ασκούν στο έδαφος οι μπροστινοί τροχοί και την αντίστοιχη δύναμη που ασκούν στο έδαφος οι πίσω τροχοί.

 Με την προϋπόθεση ότι δρουν κινητήρια μόνο οι πίσω τροχοί, να υπολογίσετε τη μέγιστη επιτάχυνση του αυτοκινήτου σε οριζόντιο έδαφος με συντελεστή τριβής 0,3.

 

( στον Παναγιώτη Χαλκιαδάκη )

 

65. Το νομίσματα θα κυλήσουν στο ορθογώνιο ˜˜˜

Δύο όμοια νομίσματα βρίσκονται στο ίδιο σημείο της πλευράς ενός ορθογωνίου, το ένα εσωτερικά, το άλλο εξωτερικά. Καταφέρνουμε να κυλήσουμε το νόμισμα που βρίσκεται εσωτερικά κατά μήκος της περιμέτρου του ορθογωνίου

 

 μέχρι να ξαναβρεθεί στην αρχική του θέση και στη συνέχεια κάνουμε το ίδιο με το άλλο νόμισμα αλλά στην εξωτερική πλευρά. Πόσες   περιστροφές έκανε κάθε νόμισμα εάν είναι γνωστό ότι το πλάτος του ορθογωνίου είναι διπλάσιο της περιμέτρου κάθε νομίσματος και ότι το μήκος είναι διπλάσιο από το πλάτος του;

( στον Παναγιώτη Παπαχρήστου )

 

66. Ποια περιοχή θερμαίνεται περισσότερο; ˜˜˜

Διαθέτουμε μια μπαταρία, δύο καλώδια και μια ομογενή μεταλλική σφαίρα. Με το ένα καλώδιο συνδέουμε τον ένα πόλο της μπαταρίας και το σημείο Α της σφαίρας. Με το άλλο καλώδιο  συνδέουμε αγώγιμα τον άλλο πόλο της μπαταρίας και το σημείο Β της σφαίρας που είναι αντιδιαμετρικό του Α. Αφήνουμε για λίγη ώρα το κύκλωμα κλειστό. Ποια από τις εγκάρσιες διατομές της σφαίρας θερμαίνεται περισσότερο;

( στον Πρόδρομο Κορκίζογλου )

 

 

67. Το δίλημμα  ˜˜˜

Ο οδηγός ενός γιωταχί τρέχει με υ χιλιόμετρα την ώρα και ξαφνικά βλέπει μπροστά του σε απόσταση d μέτρων έναν τοίχο. Τι είναι καλύτερο; Να φρενάρει  ή να στρίψει;

( στον Στέργιο Ναστόπουλο )

 

 

 

68. Το πιο γρήγορο φυσικό εκκρεμές  ˜˜˜

Από ένα κυλινδρικό μεταλλικό φύλλο κόβουμε έναν λεπτό δίσκο. Σκοπεύουμε να τον τρυπήσουμε και να τον στερεώσουμε με ένα καρφί πάνω σε τοίχο ώστε να μπορεί να αιωρείται σαν φυσικό εκκρεμές. Σε ποιο σημείο πρέπει να τον τρυπήσουμε ώστε η περίοδος για μικρά πλάτη αιώρησης να είναι η μικρότερη δυνατή;

( στον Γιάννη Τσέκερη )

 

69. Γιατί άραγε οι μετρήσεις είναι διαφορετικές;  ˜˜˜˜

Ένας φυσικός κάνει μετρήσεις της τιμής του g ( της βαρυτικής επιτάχυνσης )  σε ένα σημείο του Ινδικού ωκεανού ( πάνω στο Ισημερινό ) βασιζόμενος στις ταλαντώσεις ενός εκκρεμούς. Οι μετρήσεις γίνονται μέσα σε υποβρύχιο. Διαπιστώνεται ότι οι μετρήσεις είναι ελαφρώς διαφορετικές εάν το υποβρύχιο κινείται προς την ανατολή  οι μετρήσεις είναι ελαφρώς διαφορετικές από ότι εάν κινείται προς τη δύση μολονότι και στις δύο περιπτώσεις η ταχύτητα του υποβρυχίου είναι χρονικά σταθερή με μέτρο 0,5 m/s. Πώς θα μπορούσαμε να έχουμε προβλέψει θεωρητικώς τη διαφορά αυτή; Πόση είναι περίπου;

( στον Κώστα Κρίκο )

 

70.  Το εκκρεμές στο λεωφορείο ˜˜˜

Στην οροφή του ακίνητου λεωφορείου ο παράξενος  φυσικός έχει στερεώσει τη μία άκρη ενός νήματος  στην άλλη άκρη του οποίου έχει κρεμάσει ένα βαρίδι ώστε να διαθέτει ένα απλό εκκρεμές. Όταν το λεωφορείο είναι ακίνητο μετράει με ακριβές χρονόμετρο την περίοδο του εκκρεμούς και διαπιστώνει ότι είναι ίση με 1,54s. Μένει ικανοποιημένος με το αποτέλεσμα δεδομένου ότι έχει μετρήσει προηγουμένως το μήκος του εκκρεμούς και το έχει βρει ίσο με 60 cm. Θέλει να προβλέψει την περίοδο του εκκρεμούς

α. όταν το λεωφορείο θα κινείται σε ίσιο δρόμο με σταθερή ταχύτητα 20 m/s 

β. Όταν το λεωφορείο θα παίρνει στροφή ακτίνας 30 m με ταχύτητα μέτρου 20 m/s.

Πώς θα κάνει την πρόβλεψη;  

( στον Χρήστο Σιγάλα )

 

71.  Η κατακόρυφη ράβδος  ˜˜˜

Σε μία ομογενή κατακόρυφο ράβδο αναρτημένη από το ανώτερο σημείο της Ο και αρχικώς ακίνητη ασκείται

οριζόντια δύναμη F στο κατώτερο σημείο της Α

1. Οι ασκούμενες στη ράβδο δυνάμεις ανάγονται σε ζεύγος

2. Οι ασκούμενες στη ράβδο δυνάμεις ανάγονται σε μία οριζόντια δύναμη F

διερχόμενη από το κέντρο μάζας και σε ένα ζεύγος δυνάμεων

3. Οι ασκούμενες στη ράβδο δυνάμεις ανάγονται στην ασκούμενη

στο σημείο Α δύναμη F και σε ζεύγος δυνάμεων

4. Η ασκούμενη στη ράβδο δύναμη στο σημείο Ο είναι κατακόρυφη

5. Η ασκούμενη στη ράβδο δύναμη στο σημείο Ο έχει οριζόντια συνιστώσα

με κατεύθυνση αντίθετη της F  

6. Η επιτάχυνση του κέντρου μάζας θα είναι ίση με F/m όπου m η μάζα της ράβδου

7. Η επιτάχυνση του κέντρου μάζας θα έχει συνιστώσα προς το σημείο ανάρτησης Ο

Με ποια από τα παραπάνω συμφωνείτε;

Η ροπή αδράνειας της ράβδου ως προς άξονα κάθετο σε αυτήν - διερχόμενο από το κέντρο μάζας - είναι ίση με mL2/12

( στον Πέτρο Βατούγιο )

 

Για όλα τα προβλήματα

Η ροπή αδράνειας κάθε ομογενούς σφαιρικού σώματος  μάζας m και ακτίνας R - ως προς έναν άξονα συμμετρίας-  είναι ίση με 2/5 mR2

 κάθε ομογενούς ράβδου μάζας m  και μήκους L, ως προς άξονα συμμετρίας κάθετο σε αυτήν 1/12 mL2 

 κάθε ομογενούς δίσκου μάζας Μ και ακτίνας R ως προς άξονα συμμετρίας κάθετο στο επίπεδό του  είναι ίση με ½MR2

 κάθε ομογενούς κυλίνδρου μάζας Μ και ακτίνας R ως προς άξονα συμμετρίας κάθετο στις βάσεις είναι ίση με ½MR2

Εφόσον δεν αναφέρεται τίποτα σχετικό το κινούμενο σώμα είναι ομογενές