Το πρώτο θέμα

1. Το έτος 2005 ορίστηκε ως έτος Φυσικής και ιδιαίτερα ως έτος Einstein. To 1905 o Einstein χρησιμοποιώντας τη σωματιδιακή φύση του φωτός ερμηνευσε το φωτοηλεκτρικό φαινόμενο. Σήμερα πιστεύουμε ότι το φως συμπεριφέρεται: α. ως κύμα β. ως σωματίδιο

γ. ως κύμα και σωματίδιο δ. ως επιταχυνόμενη μάζα

2. Η σταθερά διάσπασης λ:

α. είναι μεγάλη για ραδιενεργούς πυρήνες που διασπώνται γρήγορα

β. εξαρτάται από τον αρχικό αριθμό των πυρήνων

γ. είναι ίδια για όλους τους ραδιενεργούς πυρήνες

δ. μεταβάλλεται με τον χρόνο

3. Όταν οι ακτίνες Χ προσπίπτουν σε μεταλλική πλάκα, η απορρόφηση που υφίστανται:

α. αυξάνεται όταν μειώνεται το μήκος κύματός τους

β. είναι ανεξάρτητη από το πάχος της πλάκας γ. αυξάνεται όταν μειώνεται ο ατομικός αριθμός των ατόμων του υλικού του μετάλλου της πλάκας

δ. αυξάνεται όταν μειώνεται η συχνότητα της ακτινοβολίας

4. Το ηλεκτρόνιο που εκπέμπεται από τον πυρήνα κατά τη ραδιενεργό διάσπαση β-

α. προϋπήρχε στον πυρήνα και έλκοντας τα πρωτόνιά του συνέβαλλε στη σταθερότητα του πυρήνα

β. δεν υπήρχε στον πυρήνα αλλά η εκπομπή του οφείλεται στη διάσπαση ενός νετρονίου του πυρήνα

γ. συνοδεύεται από την εκπομπή αντινετρίνου (ν_e ) για να διατηρηθεί το φορτίο στην πυρηνική αντίδραση

δ. προκαλεί μείωση του αριθμού των πρωτονίων στον θυγατρικό πυρήνα κατά 1 .

Στην παρακάτω ερώτηση 5 να γράψετε στο τετράδιό σας το γράμμα κάθε πρότασης και δίπλα σε κάθε γράμμα τη λέξη Σωστό για τη σωστή πρόταση και τη λέξη Λάθος για τη λανθασμένη

5. α. Το ατομικό πρότυπο τουRutherford ( Ράδερφορντ) αδυνατούσε να εξηγήσει τα γραμμικά φάσματα των αερίων Σ

β. Το λευκό φως όταν διαδίδεται στο κενό, εμφανίζει το φαινόμενο του διασκεδασμού Λ

γ. Στις αντιδράσεις πυρηνικής σύντηξης η μάζα ηρεμίας του τελικού πυρήνα είναι μικρότερη από το άθροισμα των μαζών των αρχικών πυρήνων Σ

δ. Τα φωτόνια γ όταν αλληλεπιδρούν με την ύλη, είτε χάνουν όλη τους την ενέργεια με μια αλληλεπίδραση κατά την οποία απορροφώνται, είτε περνούν ανεπηρέαστα. Σ

ε. Στο εσωτερικό του γυάλινου περιβλήματος των λαμπτήρων φθορισμού υπάρχει ποσότητα ατμών ιωδίου ώστε τα εξαχνούμενα άτομα βολφραμίου να επανατοποθετούνται στο νήμα Λ

Το δεύτερο θέμα

1. Να μεταφέρετε στο τετράδιό σας συμπληρωμένες τις παρακάτω αντιδράσεις:

a. ₉₂ ²³⁵U + ¹₀n ₄₂Mo + ¹³⁹ La + 2¹₀n + 7e^-

β. ⁶⁰Co ₂₈Ni + e^-+ ν_e

α. _.92 ²³⁵U + ¹₀n ⁹⁵₄₂Mo + 57¹³⁹La + 2¹₀n + 7e^-

β. 27⁶⁰Co ₂₈⁶⁰Ni + e^-+ ν_e

Για τις παρακάτω ερωτήσεις 2-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα στο γράμμα που αντιστοιχεί στη σωστή απάντηση

2. Αν ένα δείγμα ραδιενεργού υλικού έχει κάποια χρονική στιγμή ενεργότητα 8.10⁴ Bq και το ραδιενεργό υλικό έχει χρόνο υποδιπλασιασμού 60 ημέρες, τότε μετά από 120 ημέρες η ενεργότητα του δείγματος θα έχει γίνει:

α. 16.10⁴ Bq β. 2.10⁴ Bq γ. 10⁴ Bq

Να αιτιολογήσετε την απάντησή σας.

Ας συμβολίσουμε την ενεργότητα με R. Σύμφωνα με τον ορισμό της έννοιας είναι R= IdN/dtI και με βάση τον νόμο Ν=Ν₀e ^{– λt} καταλήγουμε στη σχέση R= λΝ η οποία μπορεί να χρησιμοποιηθεί χωρίς απόδειξη.

Θεωρούμε ως αρχή των χρόνων τη χρονική στιγμή που η τιμή της ενεργότητας είναι 8.10⁴ Bq - την συμβολίζουμε με R₀ – και ο αριθμός των αδιάσπαστων πυρήνων έστω Ν₀. R₀ =λΝ₀

Σε 60 ημέρες - σε χρόνο ίσο με τον χρόνο υποδιπλασιασμού – ο αριθμός των αδιάσπαστων πυρήνων θα είναι Ν₀ /2 και σε 120 ημέρες από την αρχή των χρόνων ο αριθμός των αδιάσπαστων πυρήνων θα είναι Ν₀ /4. Η τιμή συνεπώς της ενεργότητας τη στιγμή εκείνη θα είναι R= λΝ₀ /4 ,

άρα R= R₀ /4 = 2.10⁴ Bq

Σχόλιο . Ας υιοθετήσουμε επιτέλους κάποιο σύμβολο για την έννοια ενεργότητα

3. Στο πρότυπο του Bohr ( Μπορ ) για το άτομο του υδρογόνου αν είναι υ₁ η ταχύτητα του ηλεκτρονίου σε επιτρεπόμενη τροχιά με κβαντικό αριθμό n = 1 και υ₄ η ταχύτητα του ηλεκτρονίου στην επιτρεπόμενη τροχιά με κβαντικό αριθμό n = 4, τότε ισχύει

α. υ₄ =4 υ ₁ β. υ₄ = υ₁/16 γ. υ₁ = 4υ₄.

Να αιτιολογήσετε την απάντησή σας.

Α. Η συνθήκη για την κβάντωση της στροφορμής περιγράφεται με τη σχέση mυr = nh/2π στην οποία το υ παριστάνει το μέτρο της ΤΑΧΥΤΗΤΑΣ του ηλεκτρονίου, το r την ΑΚΤΙΝΑ της τροχιάς του το m τη μάζα του και το h τη σταθερά του Planck και το n ton τον ακέραιο κβαντικό αριθμό.

Β. Για την ακτίνα της τροχιάς του ηλεκτρονίου ισχύει r = n²r₁, όπου r₁ η τιμή της στην τροχιά με n = 1

Αν εφαρμόσουμε τις δύο αυτές σχέσεις για τις τροχιές με n =1 και n=4 θα έχουμε

r₄ = 4²r₁ mυ₁r₁ = h/2π mυ₄r₄ = 4h/2π για να οδηγηθούμε στην υ₁ = 4υ₄

4. Στη συσκευή παραγωγής ακτίνων Χ μεταξύ καθόδου και ανόδου εφαρμόζουμε τάση V. Υποθέτουμε ότι τα ηλεκτρόνια εξέρχονται από τη θερμαινόμενη κάθοδο με αμελητέα ταχύτητα. Η συχνότητα f_max του συνεχούς φάσματος των ακτίνων Χ μεταβάλλεται με την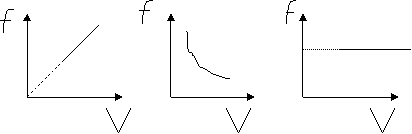

(1) (2) (3)

τάση, όπως απεικονίζεται

α. στο διάγραμμα 1 β. στο διάγραμμα 2 γ. στο διάγραμμα 3

Να αιτιολογήσετε την απάντησή σας.

Αν ΕΦΑΡΜΟΣΟΥΜΕ την ΕΞΙΣΩΣΗ ΟΡΙΣΜΟΥ της έννοιας τάση, στην περίπτωση ενός ηλεκτρονίου που μετακινείται από την κάθοδο στην άνοδο, ισχύει W = eIVI, όπου W η ενέργεια που μεταβιβάστηκε σε αυτό, ή με άλλα λόγια το έργο της δύναμης του πεδίου

Αν ΕΦΑΡΜΟΣΟΥΜΕ το ΘΕΩΡΗΜΑ ΕΡΓΟΥ ΕΝΕΡΓΕΙΑΣ για την κίνηση του ηλεκτρονίου από την κάθοδο στην άνοδο θα έχουμε Κ_αν = W , όπου Κ_αν η κινητική ενέργεια με την οποία το ηλεκτρόνιο φθάνει στην άνοδο.

Αν ΕΦΑΡΜΟΣΟΥΜΕ την εξίσωση του Planck για την ενέργεια Ε ενός συγκεκριμένου φωτονίου που θα δημιουργηθεί θα είναι Ε = hf όπου f η συχνότητα της αντίστοιχης ακτινοβολίας.

Αν συμβολίσουμε με Κ_τελ την κινητική ενέργεια του ηλεκτρονίου μετά τη «γέννηση» του φωτονίου και ΕΦΑΡΜΟΣΟΥΜΕ τη ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΕΝΕΡΓΕΙΑΣ θα είναι Κ_αν= Κ_τελ + Ε.

Ο συνδυασμός των τεσσάρων σχέσεων οδηγεί στην eIVI = Κ_τελ + hf η οποία περιγράφει τη δημιουργία ενός οποιουδήποτε φωτονίου. Από αυτήν μπορούμε να συμπεράνουμε ότι η μέγιστη συχνοτητα f_max που μπορεί να δημιουργηθεί αντιστοιχεί σε Κ_τελ = 0, είναι δηλαδή

eIVI = hf_max

Αν «δούμε» τη σχέση αυτή ως συνάρτηση με μεταβλητές τα f_max και IVI f_max = IVIe/h το αντίστοιχο διάγραμμα που θα την απεικονίζει θα είναι το (1)

Το τρίτο θέμα

Δέσμη φωτός που διαδίδεται στο κενό αποτελείται από δύο μονοχρωματικές ακτινοβολίες, την ιώδη με μήκος κύματος λ_ιω = 400nm και την ερυθρά με μήκος κύματος λ_ερ = 700nm.

Η δέσμη φωτός εισέρχεται σε γυαλί. Το γυαλί εμφανίζει για την ιώδη ακτινοβολία δείκτη διάθλασης n_ι και για την ερυθρά ακτινοβολία δείκτη διάθλασης n_ε, με λόγο n_ι/n_ε= 8/7. Το μήκος κύματος της ιώδους ακτινοβολίας στο γυαλί είναι 200nm.

α. Να υπολογιστεί ο δείκτης διάθλασης του γυαλιού για την ιώδη ακτινοβολία

Χρησιμοποιούμε τον συμβολισμό λ_0,ιω για το μήκος κύματος της ιώδους στο κενό και τον λ_γ,ιω

για το μήκος κύματος της ιώδους στο γυαλί , οπότε λ_{0,ιω =} 400nm και λ_{γ,ιω =} 200nm

ΕΦΑΡΜΟΖΟΥΜΕ την ΕΞΙΣΩΣΗ ΟΡΙΣΜΟΥ της έννοιας ΔΕΙΚΤΗΣ ΔΙΑΘΛΑΣΗΣ στην περίπτωση του γυαλιού για την ιώδη ακτινοβολία n_ι = c₀/c_γ,ιω

Εφαρμόζουμε τη ΘΕΜΕΛΙΩΔΗ ΕΞΙΣΩΣΗ ΤΩΝ ΚΥΜΑΤΩΝ για τη διάδοση της ιώδους στο κενό και στο γυαλί. c₀ = λ_0,ιω f και c_γ,ιω = λ_γ,ιω f,

όπου f η συχνότητα της ιώδους ( η οποία έχει την ίδια τιμή οπουδήποτε )

Ο συνδυασμός των τριών σχέσεων οδηγεί στην n_γ,ιω = λ_0,ιω/ λ_γ,ιω μια σχέση την οποία

- βάσει της λογικής που επικρατεί σήμερα για τη διδασκαλία- μπορεί ένας μαθητής να τη χρησιμοποιήσει και χωρίς απόδειξη. Από την αντικατάσταση προκύπτει ότι n_γ,ιω = 2

β. Να δειχθεί ότι το μήκος κύματος της ερυθράς ακτινοβολίας στο γυαλί είναι ίσο με το μήκος κύματος της ιώδους ακτινοβολίας στο κενό.

Χρησιμοποιούμε τον συμβολισμό λ_0,ερ για το μήκος κύματος της ερυθράς στο κενό και τον λ_γ,ερ

για το μήκος κύματος στο γυαλί , οπότε λ_{0,ερ =} 700nm

Με το δεδομένο n_{γ,ιω /} n_{γ,ερ =} 8/7 και με βάση το n_γ,ιω = 2 συμπεραίνουμε ότι n_{γ,ερ =} 7/4

Χρησιμοποιούμε την αντίστοιχη με την προηγούμενη σχέση του δείκτη διάθλασης και των τιμών

του μήκους κύματος και για τον δείκτη διάθλασης του γυαλιού για την ερυθρά

n_γ,ερ = λ_0,ερ/ λ_γ,ερ οπότε λ_γ,ερ = λ_0,ερ / n_γ,ερ λ_γ,ερ = 700nm / 7/4 = 400 nm

γ. Παρατηρείται αλλαγή του χρώματος της ερυθράς ακτινοβολίας κατά τη διάδοσή της μέσα στο γυαλί ; Να αιτιολογήσετε την απάντησή σας

ΟΧΙ ΒΕΒΑΙΑ. Πρόκειται για βασικό εμπειρικό δεδομένο. Το ότι «η συχνότητα ενός κύματος δεν μεταβάλλεται εφόσον η πηγή ακινητεί ως προς τον παρατηρητή» είναι θεμέλιο της κυματικής θεωρίας και δεν είναι η ΑΙΤΙΑ για το ότι το χρώμα δεν αλλάζει.

Σχόλιο. Δυστυχώς η απάντηση που ΖΗΤΕΙΤΑΙ από τον εξεταζόμενο είναι η « διότι η συχνότητα δεν μεταβάλλεται και η συχνότητα καθορίζει το χρώμα»

δ. Έστω Ν_ι και Ν_ε οι αριθμοί των φωτονίων της ιώδους και της ερυθράς ακτινοβολίας αντίστοιχα που προσπίπτουν στο γυαλί στη μονάδα του χρόνου. Να βρεθεί ο λόγος Ν_ι /Ν_ε ώστε ο ρυθμός με τον οποίο προσπίπτει η ενέργεια της ιώδους ακτινοβολίας στο γυαλί να είναι ίσος με τον ρυθμό με τον οποίο προσπίπτει η ενέργεια της ερυθράς ακτινοβολίας

Ο ρυθμός Ρ με τον οποίο μεταβιβάζεται ενέργεια – εφόσον είναι σταθερός - περιγράφεται με το πηλίκο nhf/t ή nhc/λt , ή Νhc/λ όπου Ν = n /t ο αριθμός των φωτονίων που προσπίπτουν ανά μονάδα χρόνου Ρ = Νhc/λ

ΕΦΑΡΜΟΖΟΥΜΕ τη σχέση αυτή και για την πρόσπτωση και της ιώδους και της ερυθράς οπότε

Ρ_ε = Ν_εhc/λ_0,ερ Ρ_ι = Ν_ιhc/λ_0,ιω και εφόσον Ρ_ε = Ρ_ιω θα είναι Ν_ι//Ν_ε= 4/7

Το τέταρτο θέμα

1000 άτομα υδρογόνου βρίσκονται όλα στην ίδια διεγερμένη ενεργειακή στάθμη. Για να απομακρυνθεί το ηλεκτρόνιο κάθε διεγερμένου ατόμου σε περιοχή εκτός του ηλεκτρικού πεδίου του πυρήνα, η ελάχιστη ενέργεια που απαιτείται είναι 1,51 eV.

Δίνεται η ενέργεια του ατόμου του υδρογόνου στη θεμελιώδη κατάσταση -13,6 eV.

α. Να βρεθεί ο κβαντικός αριθμός n της διεγερμένης κατάστασης στην οποία βρίσκονται τα άτομα του υδρογόνου

Α. Συμβολίζουμε με Ε_min την τιμή +1,51 eV δηλαδή την ελάχιστη τιμή ενέργειας που απαιτείται

για τη μετακίνηση του ηλεκτρονίου. Συμβολίζουμε με Ε₁ την ενέργεια (-13,6 eV) που έχει το ηλεκτρόνιο στη θεμελιώδη κατάσταση

Β. Για την τιμή της ενέργειας σε κάθε άλλη ενεργειακή στάθμη ισχύει Ε_n = Ε₁/n² , όπου n ο αντίστοιχος κβαντικός αριθμός

Γ. ΕΦΑΡΜΟΖΟΥΜΕ ΤΗ ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΕΝΕΡΓΕΙΑΣ για το φαινόμενο «μετακίνηση ενός ηλεκτρονίου από τη στάθμη με κβαντικό αριθμό n σε περιοχή εκτός του πεδίου του πυρήνα

(ιονισμός) Ε_n + Εmin = 0 δεδομένου ότι η ελάχιστη τιμή ενέργειας που έχει ένα ηλεκτρόνιο εκτός πεδίου του πυρήνα είναι μηδενική Ε_n = - Εmin και εφόσον Ε_n = Ε₁/n² θα είναι n² = - Ε₁/ Εmin n= 3

β. Να σχεδιάσετε στο διάγραμμα των ενεργειακών σταθμών όλες τις δυνατές αποδιεγέρσεις από τη διεγερμένη κατάσταση

n = 3

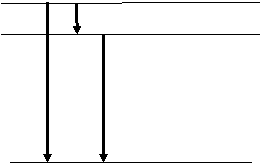n =1

γ. Από πόσες γραμμές θα αποτελείται το φάσμα εκπομπής που λαμβάνεται κατά την αποδιέγερση των 1000 ατόμων υδρογόνου

Από τρεις γραμμές

δ. Κατά την πλήρη αποδιέγερση και των 1000 ατόμων υδρογόνου εκπέμπονται συνολικά 1250 φωτόνια. Με κριτήριο την ενέργεια των εκπεμπομένων φωτονίων τα κατατάσσουμε σε κατηγορίες. Πόσα φωτόνια αντιστοιχούν σε κάθε κατηγορία;

Θα καταφύγουμε στη λογική της Άλγεβρας. Ας υποθέσουμε ότι x άτομα αποδιεγείρονται από την

n =3 στη n=1 και οτι y άτομα αποδιεγείρονται από τη n =3 στη στάθμη n =2 και στη συνέχεια στη n =1.

Κατά την αποδιέγερση των x ατόμων εκπέμπονται x φωτόνια ενώ κατά την αποδιέγερση των y εκπέμπονται 2y φωτόνια, οπότε και με βάση τα δεδομένα του προβλήματος

x + y = 1000 x + 2y = 1250 .

Έχουμε ένα σύστημα δύο εξισώσεων η λύση του οποίου μας δίνει x = 750 και y = 250

Εκπέμπονται 750 φωτόνια με ενέργεια Ε₃ –Ε₁ στο υπεριώδες

250 φωτόνια με φωτόνια με ενέργεια Ε₃ –Ε₂ στο ορατό

250 φωτόνια με φωτόνια με ενέργεια Ε₂ –Ε₁ στο υπεριώδες

ε. Ποια είναι η συνολική ενέργεια των εκπεμπομένων φωτονίων;

Α. Ένας τρόπος για να υπολογιστεί η συνολική ενέργεια Ε_ολ των εκπεμπομένων φωτονίων είναι το να πολλαπλασιάσουμε το 1000 με τη τιμή Ε₃ – Ε₁.= Ε₁/9 – Ε₁. Ε_ολ= 12090 eV.

Β. Ένας άλλος τρόπος είναι το να κάνουμε τον υπολογισμό που περιγράφει η σχέση

Ε_ολ.= 750 (Ε₃– Ε₁) + 250 ( Ε₃– Ε₂ ) + 250 ( Ε₂– Ε₁ ) = 12090 eV.