ο "μηδέν", ο "π", ο "e", o "i"

Ανδρέας Ιωάννου Κασσέτας

o μηδέν ο π, ο e, o i,

και η συγκατοίκηση

· ο Ινδός Μηδέν

· ο πανάρχαιος π

· ο ασύλληπτος e

· ο φανταστικός i

η συγκατοίκηση

Το «πάρτι» έγινε στο σπίτι του Euler. Ήταν έτος 1748 και είχαν προσκληθεί και οι πέντε. Ο Ινδός «Μηδέν», ο παγκόσμιος «Ένα» ο πανάρχαιος Έλληνας π, και οι δύο Ευρωπαίοι, ο e και ο i. Βλέπεις ο Leonhard Euler – οι Έλληνες τον λένε Όιλερ – ήταν και ο νονός των τριών από τους πέντε. Τους κάλεσε για να τους προτείνει μία δομή στην οποία θα μπορούσαν και οι πέντε να συγκατοικήσουν.

( ο αφηγητής ο οποίος εμφανίζεται ως «εκείνος» είναι ένας «μαθητής του κάποτε «που όταν μεγάλωσε δεν έγινε μαθηματικός. Έγινε φυσικός, αλλά δεν έπαψε να σαγηνεύεται από τα μαθηματικά και από την ιστορία της οικοδόμησης των επιστημονικών ιδεών )

ο ινδός « Μηδέν »

Για «εκείνον» ο αριθμός Μηδέν «ήταν και δεν ήταν» αριθμός. Όταν ήταν μικρός και μάθαινε να μετράει άρχιζε πάντα με το ένα, δύο τρία, τέσσερα . . και συνέχιζε.

Αργότερα τον Μηδέν τον φαντασίωνε σαν ένα ΑΟΡΑΤΟ ΠΛΑΣΜΑ μόνο βέβαια όταν τον έβαζε να παίζει τον ρόλο του προσθετέου. Στο πάρτι με τα αθροίσματα –στο οποίο μαζεύονταν όλοι οι αριθμοί και αλληλεπιδρούσαν μόνο με το να προστίθενται – ο Μηδέν ήταν ο αόρατος που κυκλοφορούσε στους διαδρόμους συμφιλιωμένος με τη μοναξιά του αν και συχνά τον άκουγες να ψιθυρίζει « είμαι άχρηστος, είμαι ένα μηδενικό» και ήταν σίγουρο ότι δεν είχε καμιά δυνατότητα να επηρεάσει κανέναν.

Όταν όμως τον έφερνε στο μυαλό του να λειτουργεί ως ΠΑΡΑΓΩΝ ο Μηδέν γινόταν ένας ΕΞΟΛΟΘΡΕΥΤΗΣ, ένας ανάλγητος TERMINATOR, και στο πάρτι με τα γινόμενα – στο οποίο μαζεύονταν οι αριθμοί για να πολλαπλασιαστούν μεταξύ τους –όσο και να χτύπαγε το κουδούνι δεν του άνοιγαν.

Όταν με τη φαντασία του τον έκανε ΔΙΑΙΡΕΤΗ ήξερε ότι έκανε κάτι το εντελώς απαγορευμένο. Κι όταν ο Μηδέν χτύπαγε το κουδούνι για να πάρει μέρος στο πάρτι που έκαναν οι αριθμοί και φλέρταραν διαιρούμενοι ο ένας με τον άλλον, και δημιουργώντας διάφορα πηλίκα, άκουγαν το χτύπημα και έκαναν ησυχία να μην καταλάβει ότι είναι μέσα γιατί το να διαιρεθείς μαζί του ΑΠΑΓΟΡΕΥΟΤΑΝ, μέχρι που, μια μέρα, μια αριθμός πρότεινε να του ανοίξουν και να δοκιμάσει εκείνη μαζί του ομολογώντας ότι το απαγορευμένο της ασκούσε ακατανίκητη έλξη αλλά πιστεύοντας ότι μια εμπειρία του να διαιρεθεί με τον ΜΗΔΕΝ μπορεί να την έκανε να δοκιμάσει ΓΕΥΣΗ ΑΠΟ ΑΠΕΙΡΟ.

Αρκετά χρόνια αργότερα είχε τελειώσει και το Πανεπιστήμιο είχε ακούσει ότι «τα φωτόνια έχουν μηδενική μάζα ηρεμίας» και είχε στα χέρια και το πτυχίο, την αφόρητα δηλαδή τυπική απόδειξη ότι είναι φυσικός. Και ήταν τότε που αναρωτήθηκε τι είναι σωστό «το να λέμε η ταχύτητα του τάδε αντικειμένου είναι μηδέν; » ή «να λέμε ότι είναι μηδέν μέτρα ανά δευτερόλεπτο ;». Στη γλώσσα δηλαδή των συμβόλων υ = 0 ή υ = 0 m/s . F = 0 ή F = 0 Ν; Διότι εάν ισχύει το « υ = 0 και F = 0» μήπως μας οδηγεί στο υ = F;

Όταν μεγάλωσε για τα καλά και άκουσε ότι τα μεσάνυχτα της 30^ης Δεκεμβρίου 1999 «θα γίνει» η αλλαγή του αιώνα και χιλιετίας και ότι η πρώτη Ιανουαρίου του 2000 θα εορταστεί ως πρώτη μέρα του 21^ου αιώνα και της τρίτης χιλιετίας, αναρωτήθηκε μήπως «εκείνος» που σκεφτόταν διαφορετικά είχε άδικο. Μπορεί αυτό να το επέβαλε η πανίσχυρη αγορά ο πιο δυνατός ίσως θεσμός στην κοινωνία του σήμερα αλλά το είδε κατάπληκτος ότι το αποδέχθηκαν όλες σχεδόν οι κυβερνήσεις και δισεκατομμύρια άνθρωποι. Και όλα αυτά συνέβαιναν τη στιγμή που ήταν γνωστό ότι από τότε που συγκροτήθηκαν τα ημερολόγια ΠΟΤΕ ΔΕΝ ΥΠΗΡΞΕ ΕΤΟΣ ΜΗΔΕΝ και κατά συνέπεια τα μεσάνυχτα της 30^ης Δεκεμβρίου δεν είχαν συμπληρωθεί παρά 1999 χρόνια από την αρχή της χρονολογίας μας. Ένιωσε ότι ανήκει σε μια μειοψηφία αλλά τα πράγματα προχώρησαν προς τα εκεί που είχε τεντώσει το δάκτυλό της η ανυπόμονη βασιλοπούλα αγορά. Αργότερα έμαθε ότι η είσοδος στον εικοστό αιώνα έγινε την 1^ηΙανουαρίου του 1901 και πολύ το ευχαριστήθηκε.

Το πρώτο πράγμα που συμβαίνει με τον μηδέν είναι ότι υπάρχουν δύο σχετικά διαφορετικές χρήσεις του. Αντιστοιχεί με άλλα λόγια σε δύο διαφορετικές σημασίες.

Η μία είναι ότι εκείνη που τον θέλει ως δείκτη της κενής θέσης στο σύστημα γραφής των αριθμών. Ο μηδέν είναι δηλαδή σύμβολο αναγκαίο για να δείξουμε ότι το 371 σημαίνει κάτι διαφορετικό από το 3071.

Η δεύτερη χρήση του μηδενός είναι εκείνη που τον βλέπει ως αριθμό , ανάμεσα στον +1 και στον -1. Οι άνθρωποι άργησαν να ανακαλύψουν το μηδέν κι αυτό γιατί ο μηδέν είναι μακριά από κάθε διαισθητικά αποκαλυπτόμενη μαθηματική έννοια. Τα μαθηματικά προβλήματα άρχισαν την καριέρα τους σαν προβλήματα του χώρου της πραγματικής μας ζωής - με ποσότητες που χρειάζεται να τις συγκρίνουμε - και όχι σαν προβλήματα με υψηλό επίπεδο αφαίρεσης. Στην πρώιμη εποχή των μαθηματικών οι αριθμοί – οι οποίοι ούτως ή άλλως υπήρξαν προϊόντα πρωτογενούς Αφαίρεσης- ήσαν συμπυκνωμένη σκέψη με πολύ μεγαλύτερο μερίδιο στην περιοχή του Συγκεκριμένου. Κατ΄ αρχήν έπρεπε να γίνουν τεράστια νοησιακά βήματα για να ΣΚΑΡΦΑΛΩΣΕΙ η ανθρώπινη αφαιρετική Σκέψη από το «5 άλογα» στο «5 πράγματα» κι από κει στο πολύ πιο αφηρημένο «5». Και εξυπακούεται ότι η απάντηση στο ερώτημα «τι είναι αριθμός;» δεν θύμιζε σε τίποτα την απάντηση που επικρατεί σήμερα. Αν οι μακρινοί εκείνοι πρόγονοι ήθελαν να λύσουν το πρόβλημα «πόσα άλογα θα χρειαστούν» ήταν προφανές ότι η απάντηση δεν θα μπορούσε να είναι ούτε μηδέν ούτε μείον τρία.

Οι Βαβυλώνιοι ήταν οι πρώτοι που χρησιμοποίησαν τον μηδέν όχι όμως ως αριθμό αλλά ως δείκτη.

Οι Έλληνες παρά την πρωτοποριακή θεώρηση που έκαναν στα Μαθηματικά δεν είδαν τον μηδέν ούτε ως αριθμό ούτε ως σύμβολο δείκτη για τη θέση των άλλων. Γιατί άραγε; Δύσκολη η απάντηση. Μία απόπειρα απάντησης είναι εκείνη που υποστηρίζει ότι οι τα ελληνικά Μαθηματικά ήταν κατά βάση Γεωμετρία και οι μεγάλες ελληνικές πρόοδοι βασίστηκαν σε αυτήν. Μολονότι στο ευαγγέλιο των ελληνικών Μαθηματικών, στο «Στοιχεία» δηλαδή του Ευκλείδη, εμπεριέχεται ένα «Βιβλίο πάνω στη θεωρία των αριθμών», η όλη θεώρηση βασίζεται πάνω στη Γεωμετρία. Με άλλα λόγια τα ελληνικά Μαθηματικά δεν είχαν ανάγκη να ονοματοδοτήσουν τους αριθμούς τους εφόσον τους έβλεπαν σαν μήκη ευθυγράμμων τμημάτων. Οι αριθμοί που ήταν αναγκαίο να έχουν όνομα ήταν εκείνοι που χρησιμοποιούσαν οι έμποροι και όχι οι μαθηματικοί. Υπήρχαν όμως και εξαιρέσεις και οι εξαιρέσεις αυτές ήταν οι μαθηματικοί αστρονόμοι. Μπορεί ορισμένοι ιστορικοί να υποστήριξαν ότι οι Έλληνες χρησιμοποίησαν το γράμμα όμικρον – αρχικό της λέξης ΟΥΔΕΝ - ως σύμβολο του μηδενός αλλά ο Neugebauer απέρριψε την εικασία υποστηρίζοντας πλην των άλλων ότι οι Έλληνες χρησιμοποιούσαν το όμικρον ως τον αριθμό 70. Πάντως έναν αιώνα μετά Χριστόν, ο Κλαύδιος Πτολεμαίος χρησιμοποιεί το βαβυλωνιακό μηδέν ως δείκτη.

Η ιδέα του μηδενός δείκτη θα κάνει την επανεμφάνισή της στην Ινδία ενώ το έτος 500 ο Aryabhata θα παρουσιάσει ένα σύστημα καταγραφής των αριθμών που θυμίζει το σημερινό αλλά ο μηδέν ως αριθμός δεν υπάρχει. Υπάρχουν στοιχεία που στηρίζουν την πιθανή παρουσία του μηδενός αριθμού στην Ινδία μετά το έτος 650 αλλά εκείνο που είναι ιστορικά τεκμηριωμένο είναι ότι η πρώτη ΓΡΑΠΤΗ εμφάνιση του μηδενός ως αριθμού έγινε σε ινδικό κείμενο του 876. στο οποίο τόσο ο αριθμός 50 όσο και ο 270 παρουσιάζονται με τη σημερινή γνωστή τους μορφή αν και το σύμβολο για τον μηδέν είναι σχετικά μικρότερο.

Η επινόηση του αριθμού ΜΗΔΕΝ δεν είναι μία «προφανής» συνέπεια της εξέλιξης της ανθρώπινης σκέψης. Από οποιαδήποτε σκοπιά και να το αντικρίσουμε ο μηδέν ποτέ δεν υπήρξε ένας φυσιολογικός ΥΠΟΨΗΦΙΟΣ για ΑΡΙΘΜΟΣ. Από την πρώτη εποχή της γέννησης των Μαθηματικών οι ΑΡΙΘΜΟΙ δεν ήταν τίποτε άλλο από ΛΕΞΕΙΣ αναγκαίες για την περιγραφή συσσωρεύσεων ή συγκεντρώσεων αντικειμένων. Με το κύλημα των αιώνων η έννοια ΑΡΙΘΜΟΣ γινόταν όλο και περισσότερο παιδί της Αφαίρεσης και συγχρόνως όλο και λιγότερο δημιούργημα του Συγκεκριμένου.

Η αδιάκοπη αναρρίχηση της έννοιας σε ολοένα ψηλότερα οροπέδια Αφαίρεσης άνοιξε τον δρόμο προς τη γέννηση του ινδικού Μηδέν και των ινδικών αρνητικών αριθμών, δύο εννοιών υψηλού επιπέδου Αφαίρεσης οι οποίες δεν δημιουργήθηκαν από τις ανάγκες των Ινδών να περιγράψουν «ιδιότητες της συγκέντρωσης αντικειμένων».

Η οικοδόμηση των δύο αυτών εννοιών – ΜΗΔΕΝ και ΑΡΝΗΤΙΚΟΣ ΑΡΙΘΜΟΣ – και η ενσωμάτωσή τους στο προϋπάρχον Σύστημα αριθμών, απαιτούσε, πριν απ’ όλα, την υπέρβαση της ιδέας «οι έννοιες ΜΗΔΕΝ και ΑΡΝΗΤΙΚΟΣ ΑΡΙΘΜΟΣ δεν είναι δυνατόν να είναι αριθμοί».

Αυτό όμως δεν ήταν αρκετό. Η οικοδόμηση των δύο εννοιών και η ενσωμάτωσή τους στο υπάρχον Σύστημα απαιτούσε και μία σαφή απάντηση στο ερώτημα: « Πώς θα αλληλεπιδρούν οι υποψήφιοι αυτοί με τους υπόλοιπους αριθμούς στο ζήτημα των αριθμητικών πράξεων;»

Με τρία ιδιαίτερα σημαντικά βιβλία οι Ινδοί μαθηματικοί Brahmagupta, Mahavira και Bhaskara προσπάθησαν να απαντήσουν σε αυτό το ερώτημα. Οι απαντήσεις που έδωσαν θυμίζουν την σημερινές για τον ρόλο του αριθμού Μηδέν με εξαίρεση τη διαίρεση δια του αριθμού Μηδέν την οποία ο Brahmagupta αποδέχεται, θεωρώντας το αποτέλεσμά της ως ένα κλάσμα α/0. Αποδέχεται επίσης τη διαίρεση 0/0. Ωστόσο παρά τα σημαντικά αυτά σφάλματα το έργο του Brahmagupta είναι η πρώτη – εξ όσων γνωρίζουμε σήμερα – εκπληκτική στο μέγεθός της προσπάθεια ανθρώπου να διευρύνει το σύνολο των αριθμών με τον Μηδέν και με τους αρνητικούς. Είναι μια μεγάλη στιγμή των Μαθηματικών.

200 χρόνια μετά τον Brahmagupta, ο επίσης Ινδός Mahavira θα παρουσιάσει ένα ακόμα εξαίρετο βιβλίο στο οποίο όμως θα υποστηρίξει ότι n/0 = n «εάν δηλαδή ένας αριθμός διαιρεθεί με τον Μηδέν παραμένει αναλλοίωτος». 300 περίπου χρόνια αργότερα ο επί σης Ινδός Bhaskar συμπληρώνει τους προηγούμενους με τις ισότητες 0² = 0 και Ö0 = 0 και προσπαθεί να αντιμετωπίσει το πρόβλημα της διαίρεσης με τον Μηδέν γράφοντας ότι n/0 = ∞. Και εάν βιαστούμε να το αποδεχθούμε για σωστό θα χρειαστεί να σκεφτούμε ότι εάν ισχύει θα ισχύει και ότι το γινόμενο του Μηδενός με το άπειρο θα πρέπει να δίνει οποιονδήποτε αριθμό.

Εκτός όμως από τους Ινδούς οι οποίοι γέννησαν τον Μηδέν τόσο ως αριθμό όσο και ως δείκτη υπήρξε και τουλάχιστον ένας ακόμα πολιτισμός ο οποίος χρησιμοποίησε τον μηδέν ως δείκτη. Και αυτός είναι ο πολιτισμός των Μάγια στην Κεντρική Αμερική.

Στο μεταξύ το εξαιρετικό έργο των Ινδών εξαπλώθηκε και στην Κίνα αλλά και στον αραβικό κόσμο. Τον 8^ο αιώνα το είχαν ήδη κληρονομήσει οι Άραβες. Στις αρχές του 9^ου αιώνα ο Al'Khwarizmi παρουσίασε το ινδικό σύστημα καταγραφής των αριθμών στους οποίους συμπεριέλαβε και τον Μηδέν.

Η Ευρώπη γνώρισε τόσο το ινδοαραβικό σύστημα γραφής όσο και τον Μηδέν η Ευρώπη τα έμαθε από τους Άραβες της Δύσης. Τον 12^ο αιώνα ο Ibn Ezra έγραψε τρεις πραγματείες πάνω στους αριθμούς οι οποίες συνέβαλαν στο να μεταλαμπαδευτούν τα ινδοαραβικά σύμβολα, ο Μηδέν, και οι δεκαδικοί στους Ευρωπαίους δεδομένου ότι τα κείμενά του προκάλεσαν το ενδιαφέρον των Ευρωπαίων διανοουμένων.

Ένας από τους ανθρώπους που συνέδεσαν την ευρωπαϊκή με την ινδοαραβική μαθηματική κληρονομιά ήταν ο Fibonacci. Στο Liber Abaci περιγράφει τα εννέα ινδικά σύμβολα μαζί με τον Μηδέν τον οποίο όμως δεν αντιμετωπίζει ισότιμα με τους άλλους εννέα. Η επικράτηση της ιδέας ότι ο Μηδέν είναι ένας αριθμός όπως οι άλλοι αντιμετώπισε δυσκολίες στην εξάπλωσή της. 300 χρόνια μετά τον Fibonacci, o Cardan θα λύνει τις τριτοβάθμιες εξισώσεις χωρίς να χρησιμοποιεί τον Μηδέν ή να τον θεωρεί ως πιθανή λύση. Μόνο μετά το 1600 η ιδέα για την ιδιαίτερη μαθηματική σημασία του αριθμού Μηδέν άρχισε – αν και με αντιστάσεις - να εξαπλώνεται.

Ακόμα και στην εποχή μας υπάρχουν προβλήματα κατανόησης του μηδενός. Σε πρόσφατες Πανελλήνιες εξετάσεις στη Φυσική ζητήθηκε από τους μαθητές να υπολογίσουν έναν λόγο μαζών m₁/m₂. Και ενώ με τα δεδομένα του προβλήματος η τιμή του λόγου έβγαινε ακριβώς ίση με μηδέν η ανάγνωση του αποτελέσματος δίχασε ακόμα και τους διδάσκοντες καθηγητές. Τι σήμαινε το « m₁/m₂ = 0» ; Η μία απάντηση στην οποία έδωσαν και πολλοί υψηλού επιπέδου υποψήφιοι ήταν ότι από το αποτέλεσμα « m₁/m₂ = 0» συνεπάγεται m₁= 0 πράγμα που είναι αδύνατον εφόσον το m₁παριστάνει μάζα ενός σώματος με συνέπεια να εγκαταλείψουν την προσπάθεια για λύση και τελικώς να αδικηθούν. Η απάντηση την οποία απαιτούσε η Επιτροπή των Εξετάσεων ήταν ότι από το « m₁/m₂ = 0» συνάγεται ότι η τιμή της m₂ «τείνει» στο άπειρο.

ο πανάρχαιος π

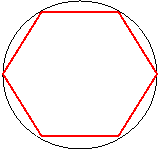Σχεδίασε ένα κανονικό εξάγωνο εγγεγραμμένο

σε κύκλο και αναρωτήθηκε «πόσες φορές

η περίμετρος είναι μεγαλύτερη από την διάμετρο

του κύκλο».

Ήξερε ότι η πλευρά του εξαγώνου είναι ίση με την

ακτίνα άρα η απάντηση ήταν εύκολη: «3 φορές».

Ας το κάνουμε τώρα δωδεκάγωνο σκέφτηκε.

Η περίμετρος θα είναι τώρα μεγαλύτερη από

την προηγούμενη. Ποιος θα είναι ο αντίστοιχος

με τον προηγούμενο «3» αριθμός;

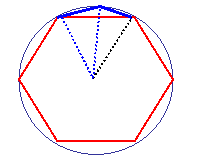Υπολόγισε ότι σε καθένα από τα 12 τρίγωνα

που θα δημιουργηθούν, η επίκεντρη γωνία θα

είναι μισή από την αντίστοιχη ( θ = 60⁰ )

στο εξάγωνο οπότε το για το μήκος της κάθε

πλευράς θα ισχύει α₁₂/2 = Rημ(θ/4)

α₁₂ = 2Rημ (θ/4) 12α₁₂ = 2R. 3,105828.

Για το 12γωνο λοιπόν ο αντίστοιχος αριθμός που

περιγράφει το «πόσες φορές η περίμετρος είναι

μεγαλύτερη από τη διάμετρο» είναι ο 3,105828.

Τι γίνεται με το 24γωνο; Η γωνία σε αυτή την περίπτωση θα είναι θ/8 ( 7,5⁰ )

α₂₄ = 2Rημ (θ/8) 24α₂₄ = = 24. 2R.ημ (θ/8) = 2R. 3,132686.

Για το 24γωνο λοιπόν ο αντίστοιχος αριθμός που περιγράφει το «πόσες φορές η περίμετρος είναι μεγαλύτερη από τη διάμετρο» είναι ο 3,132686.

Κοίταξε τους τρεις αριθμούς που ήδη διέθετε: ο 3, ο 3,105828, ο 3,132686.

Τι θα γίνει εάν συνεχίσω; σκέφτηκε; Που θα φθάσει αυτός ο αριθμός; Είχε υπομονή και κομπιουτεράκι και συνέχισε. Στο 48γωνο η περίμετρος ήταν ίση με

2R. 3,139350. Ο επόμενος δηλαδή αριθμός ήταν ο 3,139350.

Στο 96γωνο ο αριθμός έγινε 3,1410314, στο 192γωνο έγινε 3,141538944,

Είχε στο μυαλό του τον Αρχιμήδη είχε και κομπιουτεράκι αλλά ήξερε ότι το κομπιουτεράκι είχε τα δικά του όρια. Εάν θα συνέχιζα με κάποιο πιο εξελιγμένο μηχάνημα θα μπορούσα ίσως να προσεγγίσω το ερώτημα « πόσες φορές είναι μεγαλύτερη η περιφέρεια από τη διάμετρο του κύκλου, ενός δηλαδή ΟΠΟΙΟΥΔΗΠΟΤΕ ΚΥΚΛΟΥ;» να προσεγγίσω με άλλα λόγια την τιμή του π.

Σε ένα βιβλίο είχε βρει ότι με προσέγγιση 10 δεκαδικών είναι π = 3,1415926535

Ο συμβολισμός με το ελληνικό γράμμα π είναι σχετικά πρόσφατος. Ο καινούργιος επισκέπτης από το χώρο του ελληνικού αλφαβήτου εμφανίζεται για πρώτη φορά το 1706 στο έργο του Άγγλου William Johnes αλλά ο συμβολισμός θα αρχίσει να επικρατεί ΜΟΝΟ όταν τον χρησιμοποιεί ο Leonhard Euler το 1734 και θα αρχίσει να διαδίδεται στην κοινότητα των μαθηματικών μετά το 1748 όταν ο Euler δημοσιεύει το Introductio in Analysin infinitorum στο οποίο εκτός από τον συμβολισμό για τον αριθμό π παρουσιάζει και τον συμβολισμό για τον αριθμό e.

Για τους Έλληνες της εποχής του Σωκράτη το π ήταν ένας αριθμός χωρίς τον συμβολισμό με το γράμμα του αλφαβήτου ο οποίος μας λέει δύο πράγματα.

α. Το «πόσες φορές είναι μεγαλύτερη η περιφέρεια οποιουδήποτε κύκλου από την ακτίνα του» αλλά και β. το «πόσες φορές είναι μεγαλύτερο το εμβαδόν της περιφέρειας από το τετράγωνο της ακτίνας».

Ο Αντιφών και ο Βρύσων, σύγχρονοι του Σωκράτη, σκέφτηκαν να τον υπολογίσουν με βάση τα εμβαδά και δοκίμασαν να μετρήσουν το εμβαδόν του κύκλου με την πρωτοποριακή μέθοδο της εξάντλησης. Αν πάρουμε ένα εξάγωνο και διπλασιάσουμε τις πλευρές του και έπειτα τις διπλασιάσουμε ξανά και ξανά θα έχουμε τόσο πολλές πλευρές που το πολύγωνο θα γίνει κύκλος. Ο Βρύσων μάλιστα υπολόγισε τα εμβαδά δύο πολυγώνων ενός εγγεγραμμένου και ενός περιγεγραμμένου σε κύκλο και υπέθεσε ότι το εμβαδόν του κύκλου πρέπει να είναι μικρότερο από το ένα και μεγαλύτερο από το άλλο.

Διακόσια περίπου χρόνια αργότερα ανέλαβε τη μέτρηση ο Αρχιμήδης. Για τους υπολογισμούς του χρησιμοποίησε τη μέθοδο της εξάντλησης του Αντιφώνος και του Βρύσωνος αλλά έστρεψε την προσοχή του στις περιμέτρους των πολυγώνων και όχι στα εμβαδά τους. Διπλασίασε τις πλευρές των αρχικών εξαγώνων έσσερις φορές καταλήγοντας σε δύο 96γωνα το ένα εγγεγραμμένο και το άλλο περιγεγραμμένο στον κύκλο. « Παντός κύκλου η περίμετρος της διαμέτρου εστί και έτι υπερέχει ελάσσονι μεν ή εβδομω μέρει της διαμέτρου, μείζονι δε ή δέκα εβδομηκοστομόνοις ».

Η τιμή δηλαδή του π ήταν μεγαλύτερη από 3 + 1/7 = 3,1428571 και μικρότερη από 3 + 10/71 = 3,140845. Αν υπολογίσουμε τη μέση τιμή των δύο αυτών αριθμών παίρνουμε την τιμή 3,1419 μία τιμή που διαφέρει μόνο κατά 3/10000 από τη σήμερα αποδεκτή.

Στους αιώνες που ακολούθησαν η τιμή του π κυνηγήθηκε από τους μεγαλύτερους μαθηματικούς της Ιστορίας. Ανάμεσά τους ήταν:

o Κλαύδιος Πτολεμαίος κατά τις αρχές του 2^ου αιώνα στην Αλεξάνδρεια π = 3+17/120 ή π = 3,14167

o Τσανγκ Χονγκ στις αρχές του 2^ου αιώνα στην Κίνα π = Ö10 ή π = 3,16227

Η τιμή π = Ö10, μολονότι σχετικά ανακριβής, είναι εύχρηστη και ευκολομνημόνευτη και παρέμεινε για αρκετά χρόνια δημοφιλής στην Ασία

o Γουάνγκ Φάου τον 3^ο αιώνα στην Κίνα π = 142/45 ή π = 3,15555

o Τσου Τσουνγκ-τσιχ υάνγκ τον 5^ο αιώνα στην Κίνα π = 3,1415929

χρησιμοποιώντας εγγεγραμμένα πολύγωνα με 14.576 πλευρές

o Αριαμπάτα τον 6^ο αιώνα στις Ινδίες π = 3,1416

o Βραχμαγκούπτα τον 7^ο αιώνα στις Ινδίες π =Ö10 ή π = 3,16227

Με δεδομένο ότι η τιμή π =Ö10 (=3,16227) μαθαίνεται και απομνημονεύεται εύκολα διαδόθηκε από τις Ινδίες στην Ευρώπη και χρησιμοποιήθηκε από τους μαθηματικούς όλου του κόσμου στη διάρκεια του Μεσαίωνα

o Francois Viete το 1579 στη Γαλλία έδωσε την ακριβέστερη μέχρι τότε τιμή

3,1415926537 > π > 3,1415926535

o Snell το 1621 στην Ολλανδία 3,14160 > π >3,14022

o Huygens το 1650 στην Ολλανδία 3,1415926533 >π> 3,1415926538

o John Wallis το 1655 στην Αγγλία π ₌ _{2.2.4.4.6.6.8.}

² ^{1.3.3.5.5.7.7.}

o Leonhard Euler

π/2 = (3/2).(5/6).(7/6).(11/10).(13/14).(19/18).(23/22)

π²/6 = 1/1² + 1/2² + 1/3² + 1/4² + 1/5² + 1/6² + .

απ’ όπου με προσέγγιση 25 δεκαδικών

π = 3,1415926535897932384626433

ο «ασύλληπτος» e

Ο e. Αν ζητήσεις από ένα φυσικό να τον κοιτάξει στα μάτια το πιθανότερο είναι να σου πει «βλέπω ένα ηλεκτρόνιο». Ο μαθηματικός όμως θα σου πει ο «ι» διαβάζοντας το γράμμα e στα αγγλικά και ίσως να συμπληρώσει είναι ότι είναι ένας αριθμός μεγαλύτερος από το 2 και μικρότερος από το 3, ίσος με 2,72 περίπου.

Εκείνος είχε μάθει τότε στο σχολείο ότι lne = 1 ή e^lna= a και ότι ο e είναι « η βάση των νεπέριων λογαρίθμων» ή «η βάση των φυσικών λογαρίθμων» και είχε βάλει στον εαυτό του το ερώτημα «τι έχουν αυτοί οι λογάριθμοί που τους κάνει να λέγονται ΦΥΣΙΚΟΙ»; Πάντα όμως αναρωτιόταν «γιατί άραγε οι άνθρωποι ως βάση των φυσικών λογαρίθμων διάλεξαν τον παράξενο αυτό αριθμό και όχι έναν άλλο πιο απλό, έναν ακέραιο λόγου χάρη όπως είναι ο 2 ή ο 10;». Αργότερα βέβαια πρόσεξε την ιδιαιτερότητα που είχε μία εκθετική συνάρτηση όταν η βάση ήταν ο e. Του έκανε δηλαδή εντύπωση ότι η παράγωγος της y = e^x ήταν ίση με e^x ενώ η παράγωγος της y = 2^xδεν ήταν ίση με 2^x.

Αργότερα έμαθε ότι ο e «κυκλοφορεί» και

ως ΟΡΙΟ της (1+1/n)ⁿ όταν η τιμή του n τείνει στο άπειρο

αλλά «κυκλοφορεί» και ως ΑΘΡΟΙΣΜΑ άπειρων όρων της σειράς

1/1! +1/2! + 1/3! + 1/4! + 1/5!. . .

Ο e ΟΡΙΟ, ο e ΑΘΡΟΙΣΜΑ ο e βάση των φυσικών λογαρίθμων, ο e^x με την ιδιαιτερότητα στην παραγώγιση, του ήταν δύσκολο να συνθέσει το παζλ.

Σε σχέση με τον ηλικίας 2500 χρόνων πανάρχαιο «π», ο «e» είναι ένας νεαρός ηθοποιός στο έργο μαθηματικά, είναι ένας αριθμός ηλικίας 300 περίπου ετών πέραν όμως αυτού οι διαδρομές των δύο αυτών αριθμών διαφέρουν ιδιαίτερα

Ο Euler ήταν ο πρώτος που χρησιμοποίησε το γράμμα ως σύμβολο για τον αριθμό αυτόν το 1727 γι αυτό και συχνά αναφέρεται ως αριθμός Euler ενίοτε όμως και ως σταθερά του Napier

Η πρώτη εμφάνιση του e γίνεται με χαμηλούς τόνους το 1618 με τον πίνακα των λογαρίθμων του Napier. Είναι όμως ένας αριθμός χωρίς όνομα και χωρίς κάποιο ειδικό σύμβολο. Ωστόσο το γεγονός ότι «οι λογάριθμοι του Napier ήταν λογάριθμοι με βάση το e» δεν μπορούσε να αναγνωριστεί διότι η έννοια λογάριθμος στην πρώτη της αυτή παρουσίαση δεν είχε τη σημασία που έχει σήμερα. Το ότι ο λογάριθμος ενός αριθμού είναι ο εκθέτης στον οποίο πρέπει να «υψωθεί» κάποια συγκεκριμένη ΒΑΣΗ για να μας δώσει τον αριθμό είναι ένας μεταγενέστερος τρόπος θεώρησης της έννοιας.

Στα μέσα περίπου του αιώνα οι έννοιες αυτές σχετίστηκαν με την ισοσκελή υπερβολή Το 1647, στη Bruge, ο γαλλόφωνος Ιησουίτης Gregoire de Saint Vincent υπολόγισε το εμβαδόν κάτω από μία ισοσκελή υπερβολή.

Το εάν μπόρεσε να διακρίνει τη σύνδεση με τους λογαρίθμους είναι προς συζήτηση.

Το 1661 ο Huygens «είδε» τη ΣΧΕΣΗ ανάμεσα στην υπερβολή xy =1 και στον λογάριθμο. Και ο αριθμός e είναι τέτοιος ώστε

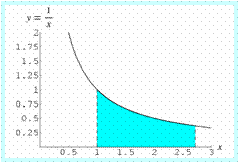EAreaPlot το εμβαδόν – το ολοκλήρωμα – κάτω

από την υπερβολή από 1 έως e

να είναι ίσο με 1

ΚΑΙ ΑΥΤΗ ΕΙΝΑΙ Η ΙΔΙΟΤΗΤΑ

ΠΟΥ ΤΟΝ ΚΑΝΕΙ ΝΑ ΕΙΝΑΙ

«ΒΑΣΗ ΤΩΝ ΦΥΣΙΚΩΝ ΛΟΓΑΡΙΘΜΩΝ».

Αυτό όμως δεν είχε κατανοηθεί από τους μαθηματικούς της εποχής αν και το είχαν πλησιάσει

( με σύγχρονη σημειογραφία ò¹_edx/x= ¹_e[ ln x] = lne - ln1 =1 )

Το 1668 ο Nicolas Mercator δημοσιεύει το Logarithmotechnia στο οποίο περιλαμβάνεται το ανάπτυγμα σε σειρά της συνάρτησης y = log(1+x). Στο έργο του χρησιμοποιεί τον όρο ΦΥΣΙΚΟΣ ΛΟΓΑΡΙΘΜΟΣ ln(1 + x) = x - x²/2 + x³/3 - x⁴/4 +..

15 περίπου χρόνια αργότερα ο e φαίνεται να ανακαλύπτεται όχι όμως μέσω της έννοιας «λογάριθμος» ούτε και μέσω της Αναλυτικής Γεωμετρίας .

Το 1683 ο Jacob Bernoulli μελετώντας τις συνεχείς συναρτήσεις, επιχειρεί να προσδιορίσει το ΟΡΙΟ της (1 + 1/n)ⁿόταν το n τείνει στο άπειρο. Χρησιμοποιεί το διωνυμικό θεώρημα

(α+β)ⁿ= αⁿ +n_/1!αⁿ^-1β + n(n-1)_/_2! αⁿ^-2β² + n(n-1) (n-3)_/3! + . .+ n(n-1) . . 2_/(_n_-1)!_aαβⁿ^-1 + βⁿ

για να αποδείξει ότι το όριο ήταν ανάμεσα στους αριθμούς 2 και 3 και μπορούμε να δεχθούμε ότι αυτή ήταν και η πρώτη προσέγγιση για τον προσδιορισμό του e.

Ο ίδιος δέχτηκε ότι το ζητούμενο όριο ήταν ένας ΟΡΙΣΜΟΣ του αριθμού e . Ήταν η πρώτη φορά που χρησιμοποιήθηκε η πρακτική του «ένας αριθμός να ορίζεται από κάποιο όριο». Ωστόσο δεν μπορούσε να διακρίνει κάποια σύνδεση του οριζόμενου αυτού αριθμού και της έννοιας λογάριθμος δεδομένου ότι την εποχή εκείνη η έννοια λογάριθμος δεν είχε ως σημαινόμενο αυτό που έχει στην εποχή μας.

Σήμερα από την εξίσωση x = a^t συμπεραίνουμε ότι t = logx όπου ο λογάριθμος έχει ως βάση το α, αλλά αυτό είναι μία θεώρηση που εδραιώθηκε αργότερα. Για τους μαθηματικούς της εποχής εκείνης ο λογάριθμος δεν παραπέμπει σε συνάρτηση και δεν είναι παρά ένας αριθμός που μπορεί να βοηθήσει στους υπολογισμούς.

Και ίσως ο Jacob Bernoulli να είναι ο πρώτος που «υπέθεσε » ότι η λογαριθμική συνάρτηση είναι το αντίθετο της εκθετικής. Πάντως το 1684 ο James Gregory «είδε» καθαρά ότι τον δεσμό ανάμεσα στους λογαρίθμους και στους εκθέτες, δεν είναι όμως βέβαιο ότι ήταν ο πρώτος.

Εξ όσων γνωρίζουμε η πρώτη φορά που στον e αποδόθηκε η σημερινή σημασία ήταν το 1690 και «δράστης» ο Leibniz. Tη χρονιά εκείνη έγραψε μια επιστολή στον Huygens μια επιστολή στην οποία χρησιμοποίησε τον συμβολισμό b αντί για τον σύγχρονο e. Για πρώτη φορά ο αριθμός αυτός είχε ένα συμβολισμό και ήταν αναγωρίσιμος.

Από τη στιγμή που ο αριθμός απέκτησε ΤΑΥΤΟΤΗΤΑ έγινε φανερό ότι οι – μετά τον Napier- πρώιμες εργασίες είχαν σχέση με αυτόν. Αναδρομικά δηλαδή αναγνωρίστηκε ότι οι πρώιμες επεξεργασίες της έννοιας λογάριθμος απετέλεσαν μέρος της προσπάθειας για την οικοδόμησή του.

Είχε έλθει πλέον η εποχή που θα εμφανιζόταν στο προσκήνιο ο Euler.

Η πρόταση που έκανε ήταν να συμβολίζεται ο αριθμός με το γράμμα e και το πιθανότερο η ιδέα για το γράμμα e η οποία και επεκράτησε

σχετίζεται με το αρχικό της λέξης exponential. Ο συμβολισμός εμφανίζεται σε μία επιστολή του στον Goldbach χρονολογημένη το έτος 1731. Τον χρησιμοποιεί για πρώτη φορά το 1736 στο Mecanica και μερικά χρόνια αργότερα και αφού προηγήθηκαν ιδιαίτερες νοησιακές προσπάθειες το 1748 δημοσιεύει το Introductio in Analysin infinitorum στο οποίο παρουσιάζει μία πλήρη έκθεση των ιδεών γύρω από τον αριθμό e.

Αποδεικνύει ότι ο e είναι ίσος με 1 + 1/1! + 1/2! + 1/3! +. . . .

Υπολογίζει την τιμή e = 2.718281828459045235 με προσέγγιση 18 δεκαδικών ψηφίων

Αποδεικνύει ότι ο e είναι το όριο της (1 + 1/n)ⁿ όταν το n τείνει στο άπειρο

Αποδεικνύει τη σχέση e^ix= cosx + isinx βασιζόμενος στη φόρμουλα του De Moivre

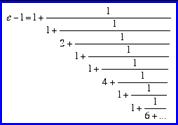
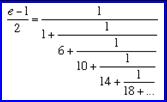Παρουσιάζει

το ανάπτυγμα καθώς και το

Οι περισσότεροι ιστορικοί αποδέχονται ότι ο Euler ήταν ο πρώτος που απέδειξε ότι ο e είναι άρρητος. Τον επόμενο αιώνα – 1873 – ο Hermite αποδεικνύει ότι ο e είναι ΥΠΕΡΒΑΤΙΚΟΣ αριθμός και όχι αλγεβρικός δεν μπορεί δηλαδή να είναι λύση οποιασδήποτε εξίσωσης με ρητούς συντελεστές Το εάν ο e^e είναι αλγεβρικός αριθμός είναι ένα ανοικτό ακόμα και σήμερα ζήτημα. Πρόσφατα έχει αποδειχθεί ότι από τους δύο αριθμούς e^e και e εις την δύναμη e^e² τουλάχιστον ο ένας είναι ΥΠΕΡΒΑΤΙΚΟΣ.

Τελικά τι είναι ο e; Ποιος είναι ο αποδεκτός ΟΡΙΣΜΟΣ του;

Οι επικρατέστεροι σήμερα ορισμοί για τον e είναι τρεις:

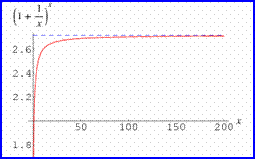ELimit 1. e ονομάζεται το ΟΡΙΟ της

(1 + 1/n)ⁿ όταν το n τείνει στο άπειρο

$e = \lim_{n\to\infty} \left(1+\frac{1}{n}\right)^n$

2. e ονομάζεται το ΑΘΡΟΙΣΜΑ των απείρων όρων της σειράς

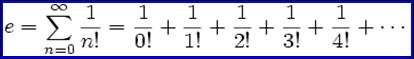
$e = \sum_{n=0}^\infty {1 \over n!} = {1 \over 0!} + {1 \over 1!} + {1 \over 2!} + {1 \over 3!} + {1 \over 4!} + \cdots$

3. e ονομάζεται ο μοναδικός αριθμός x>0

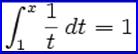$\int_{1}^{x} \frac{1}{t} \, dt = {1}$ για τον οποίο ισχύει

Τρεις ορισμοί ισοδύναμοι. Για τον πρώτο από τους ορισμούς επιστρατεύεται η έννοια ΟΡΙΟ, για τον δεύτερο η έννοια ΣΕΙΡΑ ΑΠΕΙΡΩΝ ΟΡΩΝ και για τον τρίτο η έννοια ΟΛΟΚΛΗΡΩΜΑ. Έχει ωστόσο αποδειχθεί ότι οι τρεις διαφορετικοί ορισμοί είναι ισοδύναμοι.

e = 2.71828 18284 59045 23536 02874 7135...

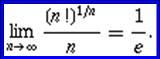
lim_(n->infty)((n!)^(1/n))/n==1/e.

Ο τύπος του Stirlings

Το πρόβλημα του Steiner.

«Ποια είναι η μέγιστη τιμή του x^1/x»;

Και η απάντηση: η e^1/e.

Η εκθετική συνάρτηση και η Φυσική

Το φαινόμενο «ραδιενεργός εκπομπή» Ν = Ν₀e^-λt

Το φαινόμενο «φθίνουσα ταλάντωση» Α =Α₀e^-λt

Το φαινόμενο «εκφόρτιση πυκνωτή» q = q₀e^-^t^/^RC

Το φαινόμενο «ελάττωση του ρεύματος» κατά το κλείσιμο του διακόπτη σε ένα πηνίο» i=i₀e^-^tR^/^L

ο «φανταστικός» i

Συμβολίζεται με το γράμμα i αρχικό της γαλλικής λέξης imaginaire και στο σχολείο τον φώναζαν με το όνομα «γιωτ». Ήταν ο αριθμός γιωτ.

«Εκείνος» συναντήθηκε μαζί του τέσσερα χρόνια μετά την αποφοίτηση από το Δημοτικό, όταν άκουσε από τον καθηγητή των μαθηματικών ότι «υπάρχουν λύσεις στη δευτεροβάθμια ακόμα κι αν η διακρίνουσα είναι αρνητική». Μέχρι τότε διάβαζε στο βιβλίο των μαθηματικών ότι «λύσεις δεν υπάρχουν γιατί τετραγωνική ρίζα αρνητικού αριθμού δεν υφίσταται».

Και η x² + 4x + 6 = 0, τις οποίας οι δύο ρίζες είναι η «-2+ Ö(-2)» και η «-2- Ö(-2)», «δεν έχει ρίζες» διότι Ö(-2) δεν υφίσταται.

Και ενώ όλα αυτά τα έβρισκε λογικά, μπήκε εκείνη την ημέρα στην τάξη ο καθηγητής των μαθηματικών τους μίλησε για φανταστικούς και για μιγαδικούς αριθμούς και τους έμαθε να λένε ότι οι δύο λύσεις της x² + 4x + 6 = 0 είναι η «– 2+2i» και η «– 2+2i».

Μερικά χρόνια αργότερα φοιτητής πια του φυσικού στο Πανεπιστήμιο της Αθήνας είχε μια ενδιαφέρουσα συνάντηση με την τριγωνομετρική μορφή κάθε μιγαδικου αριθμού την z = ρ(συνx + iημx ) και με το θεώρημα του Abraham de Moivre

(συνx + iημx)ⁿ = συνnx + iημnx κaθώς και με τη σχέση που τη συνόδευε το όνομα Euler, την e^ix = συνx + iημx

Βέβαια η παρουσία των παράξενων αυτών αριθμών αυτών αριθμών έγινε στοιχείο απαραίτητο για την περιγραφή της συμπεριφοράς ορισμένων ηλεκτρικών κυκλωμάτων και πάνω απ’ όλα για τη συγκρότηση της εξίσωσης Schröndinger, τότε που κατάλαβε ότι η τιμή της κυματοσυνάρτησης Ψ ήταν ένας μιγαδικός αριθμός.

Ο γιωτ έκανε μια πρώιμη εμφάνιση στη σκηνή της Ιστορίας των Μαθηματικών, τον 16^ο αιώνα κατά την εποχή που οι Ιταλοί μαθηματικοί προσπαθούν να βρουν τρόπους για τη λύση τριτοβάθμιων εξισώσεων όπως η x³ + x = 2.

Το 1572 ο Rafaello Bombelli, ο τελευταίος μεγάλος μαθηματικός της Bologna, παρουσίασε το βιβλίο του Algebra, στο οποίο μελετώντας τις τετραγωνικές ρίζες διάφορων αριθμών σκόνταψε σε ένα αναπάντητο ερώτημα: «Ποια είναι η τετραγωνική ρίζα του αρνητικού αριθμού -1» ; Η λύση γι αυτόν ήταν να «δημιουργήσει» έναν καινούριο αριθμό και θα είναι εξ ορισμού η απάντηση στο ερώτημα «ποια είναι η τετραγωνική ρίζα της αρνητικής μονάδας;».

Βέβαια θα μπορούσε κανείς να αντιτάξει ότι «τέτοιου είδους αριθμού δεν κυκλοφορεί στις γειτονιές της Πραγματικότητας» αλλά η πρόταση έθετε επί τάπητος τα ερωτήματα «τι είναι αριθμός;» και «τι είναι Πραγματικότητα;».

Εξάλλου μία ανάλογη απάντηση σε διαφορετικό βέβαια ερώτημα είχε δοθεί από τους Ινδούς μαθηματικούς πριν από αρκετούς αιώνες. Ήταν τότε που η ανάγκη για μία απάντηση στο ερώτημα «με τι ισούται η διαφορά 1-2 ; » είχε οδηγήσει στην επινόηση των αρνητικών αριθμών . Μήπως οι αρνητικοί αριθμοί κυκλοφορούν στις λεωφόρους της Πραγματικότητας;

Στη συγκεκριμένη περίπτωση της τετραγωνικής ρίζας του «-1 » μία σημασιακή διεύρυνση της έννοιας ΑΡΙΘΜΟΣ θα μπορούσε να είναι τέτοια ώστε να χωρέσει και το καινούριο πλάσμα της ανθρώπινης αφαιρετικής σκέψης. Και αυτό συνέβη. Ο Bombelli «έσπρωξε» στο παλκοσένικο της ιστορίας των Μαθηματικών αριθμούς όπως ο R[Om. 9] -στον οποίο το R παριστάνει την τετραγωνική ρίζα και το m το πρόσημο «μείον» και τον οποίο θα συμβολίζαμε σήμερα με Ö(0-9) - .

Ο αλλόκοτος αυτός αριθμός, γέννημα θρέμμα της Ευρώπης, που χαρακτηρίστηκε από τον Descartes «imaginaire» – στην ελληνική γλώσσα «φανταστικός»- έκανε την εμφάνισή του χωρίς να συμβολίζεται με κάποιο γενικώς αποδεκτό σύμβολο. Εκατό περίπου χρόνια μετά τους Ιταλούς, προς το τέλος δηλαδή του 17^ου αιώνα, ο Leibniz θα περιγράψει εύστοχα την παράξενη φύση του:

«ο φανταστικός αριθμός είναι μία λεπτή επινόηση του ανθρώπινου πνεύματος ένα αμφίβιο σχεδόν ον ανάμεσα στο ον και στο μη ον».

Ο φανταστικός αριθμός γεννήθηκε λοιπόν τον 16^ο αιώνα και απέκτησε τον δικό του «παγκόσμιο» συμβολισμό με το γράμμα i τον 18^ο αιώνα ύστερα από πρόταση του Euler.

i²=-1 i³=-i i⁴=1 i⁵=-i i⁶=-1.

Από κει και πέρα ο «i» απετέλεσε τη λεγόμενη φανταστική μονάδα από την οποία μπορούμε να δημιουργήσουμε φανταστικά κλάσματα όπως το 3i/4, αριθμούς όπως ο «- 5i» ο οποίος δεν είναι ούτε μικρότερος ούτε μεγαλύτερος από το μηδέν -διότι η σύγκρισή του με το μηδέν δεν έχει νόημα- αλλά και άρρητα πολλαπλάσια της φανταστικής μονάδας όπως ο «- Ö13i».

Η εισαγωγή των φανταστικών αριθμών ανάγκασε τους μαθηματικούς να δημιουργήσουν την έννοια «πραγματικός αριθμός» και να χαρακτηρίζουν όλους τους άλλους αριθμούς ως ΠΡΑΓΜΑΤΙΚΟΥΣ.

Το άθροισμα ενός φανταστικού και ενός πραγματικού αριθμού, όπως λόγου χάρη ο 7+ 2i, συνιστά τον λεγόμενο ΜΙΓΑΔΙΚΟ αριθμό ο οποίος συμβολίζεται με το λατινικό γράμμα z.

Το πρόβλημα βέβαια που δημιουργήθηκε είναι ότι όλοι αυτοί οι φανταστικοί και οι μιγαδικοί αριθμοί δεν έχουν θέση στην ευθεία των πραγματικών αριθμών. Οι μαθηματικοί όμως ξεπέρασαν και αυτή τη δυσκολία δημιουργώντας, την ευθεία των φανταστικών αριθμών κάθετη στην ευθεία των πραγματικών αριθμών και από τότε, ενώ οι πραγματικοί εξακολουθούν να κυκλοφορούν στη δική τους ευθεία, οι φανταστικοί «ζουν» πάνω στην άλλη. Όσο για τους μιγαδικούς, αυτοί ζουν στο επίπεδο των δύο αυτών ευθειών.

Στο μεταξύ, πριν δηλαδή και από την παρέμβαση του Euler, είχε προταθεί τόσο η τριγωνομετρική αναπαράστασή κάθε μιγαδικού αριθμού

z = ρ( συνx + iημx) όσο και το λεγόμενο θεώρημα de Moivre σύμφωνα με το οποίο « αν z = ρ( συνx + iημx) τότε zⁿ = ρⁿ(συνnx + iημnx)» στοιχεία τα οποία χρησιμοποίησε ο Euler για τη σύνδεσή του με τον αριθμό e.

η συγκατοίκηση

Εάν στην εξίσωση του Euler e^ix = συνx + iημx

βάλουμε x = π θα προκύψει η σημαντικότερη - κατά τον Feynman- σχέση των μαθηματικών

eⁱ^π +1=0

Ο Benjamin Peirce σε μία του διάλεξη, αναφερόμενος στην απίστευτη αυτή ισότητα είχε πει :

“Gentlemen, that is surely true, it is absolutely paradoxical; we cannot understand it, and we don't know what it means. But we have proved it, and therefore we know it must be the truth."

Κύριοι, είναι σίγουρα αληθής, είναι απολύτως παράδοξη. Δεν μπορούμε να την κατανοήσουμε και δεν ξέρουμε τι σημαίνει. Αλλά την έχουμε αποδείξει και γι αυτό ξέρουμε ότι είναι αληθής

Ο Richard Feynman τη θεωρούσε την πιο σημαντική φόρμουλα των μαθηματικών δεδομένου ότι σ΄ αυτήν συγκατοικούν οι πέντε σημαντικότεροι αριθμοί των μαθηματικών, ο 1, ο «0», ο π, ο e και ο i .

iⁱ= πραγματικός ;

Εάν στην εξίσωση του Euler e^ix = cosx + isinx βάλουμε x = π/2 θα προκύψει

eⁱ^π/2 = cosπ/2+ isinπ/2. eⁱ^π/2 = i

Αν υψώσουμε και τα δύο μέλη στη δύναμη i προκύπτει e^-π/2 = iⁱ

iⁱ =e^-π/2 = 0,2078795763