Μια λύση με λάθος την κατεύθυνση της τριβής

( Βρέθηκε σε δεκάδες γραπτά )

Ανδρέας Ιωάννου Κασσέτας

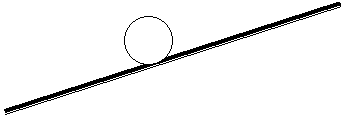
Β_X

T

- Τ- mg_x = ma_cm

TR = 2/5mR²α_γων

a_cm= a_γωνR άρα

a_cm = -5/7g_x a_cm = - 4 m/s²

Καταλήγει σε σωστό αποτέλεσμα.

Η ερώτηση: Υπάρχει άραγε λάθος και εάν ΝΑΙ που βρίσκεται;

Η απάντηση:

Δεν είναι μόνο το ότι έχει σημειωθεί λανθασμένα η στατική τριβή. Είναι και ότι οι αλγεβρικές σχέσεις δεν έδειξαν τη λάθος κατεύθυνση της τριβής. Ας τις δούμε:

- Τ- mg_x = ma_cm ΣΩΣΤΟ εάν δεχθούμε ότι ο προσανατολισμός του άξονα x γίνεται με + προς τα πάνω δεξιά και ότι τα σύμβολα Τκαι mg_x παριστάνουν τα μέτρα των αντίστοιχων μεγεθών (Τ > 0 , mg_x .> 0 ) ενώ το a_cm παριστάνει την αλγεβρική τιμή της επιτάχυνσης

TR = 2/5mR²α_γων ΛΑΘΟΣ

a_cm= a_γωνR ΛΑΘΟΣ

a_cm = -5/7g_x ΣΩΣΤΟ

Γιατί όμως οι δύο σχέσεις είναι και οι δύο ΛΑΘΟΣ; Δύσκολη η απάντηση

Ας δούμε τη λύση με αλγεβρικές τιμές

Β_X

T

Τ+mg_x = ma_cm (1) Η εξίσωση με τον δεύτερο νόμο απαιτεί κάποιο προσανατολισμό του

άξονα x. Μόνο σε σχέση με αυτόν τον προσανατολισμό οι αλγεβρικές τιμές των μεγεθών αποκτούν αλγεβρική υπόσταση

TR = 2/5mR²α_γων (2) Η εξίσωση αυτή συσχετίζει αλγεβρικές τιμές μεγεθών ( ροπή και γωνιακή επιτάχυνση ) τα οποία αντιστοιχούν σε διανύσματα κάθετα στο επίπεδο του σχήματος. Για να λειτουργήσει συνεπώς απαιτεί κάποιο προσανατολισμό ενός άλλου άξονα του z , κάθετου στο σχήμα .

Για να είναι όμως συμβατές και οι δύο εξισώσεις, για να μπορεί δηλαδή το σύμβολο Τ να είναι κάτι ΘΕΤΙΚΟ ( ή αρνητικό ) ΚΑΙ ΣΤΙΣ ΔΥΟ πρέπει ο συνδυασμός των δύο προσανατολισμών να μην οποιοσδήποτε. Από τους τέσσερις συνδυασμούς των δύο προσανατολισμών

x + δεξιά πάνω (δ) και z + Ⓧ

x + δεξιά πάνω (δ ) και z + προς τα έξω

x + αριστερά κάτω ( α ) και z + Ⓧ

x + αριστερά κάτω ( α ) και z + προς τα έξω

μόνο οι δύο είναι συμβατοί

Ο x + δ και z + προς τα έξω

Και Ο x + α και z + Ⓧ

Με βάση αυτή τη σύμβαση η σχέση των αλγεβρικών τιμών των a_cm και a_γων

είναι η a_cm= - a_γωνR (3) . Από τις τρεις σχέσεις προκύπτει a_cm = 5/7g_x

Εξυπακούεται βέβαια ότι μπορούμε να λύσουμε το πρόβλημα χρησιμοποιώντας τα μέτρα των αντίστοιχων μεγεθών

Ας δούμε και τη λύση με μέτρα.

Τ- mg_x = ma_cm TR = 2/5 mR²α_γων a_cm= a_γωνR

a_cm = 5/7g_x a_cm = 4m/s²

Και ορισμένα συμπεράσματα

1. Κατά τη μελέτη του φαινομένου ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ η χρήση ΑΛΓΕΒΡΙΚΩΝ ΤΙΜΏΝ των διανυσματικών μεγεθών θέση, ταχύτητα, επιτάχυνση, δύναμη είναι αναγκαία

2. Κατά τη μελέτη του φαινομένου ΚΡΟΥΣΗ και ειδικά κατά την εφαρμογή της Διατήρησης της ορμής η χρήση ΑΛΓΕΒΡΙΚΩΝ ΤΙΜΏΝ για τα διανυσματικά μεγέθη ταχύτητα και ορμή είναι κατά τη γνώμη μας προτιμότερη και πιο κομψή από τη χρήση μέτρων για τα αντίστοιχα μεγέθη

3. Κατά τη μελέτη του φαινομένου ΚΥΛΙΣΗ όταν χρειαστεί να παρουσιάσουμε σχέσεις διανυσματικών μεγεθών σε δύο κάθετους άξονες η χρήση των ΜΕΤΡΩΝ των διανυσματικών μεγεθών είναι, από τη σκοπιά της Διδακτικής, προτιμότερη από τη χρήση αλγεβρικών τιμών.