Ανδρέας Ιωάννου Κασσέτας

Το ερώτημα

Κατά την εξέλιξη του φαινομένου ΚΥΛΙΣΗ μπορεί κανείς να εφαρμόσει το θεώρημα έργου ενέργειας

ΜΟΝΟ για τη ΜΕΤΑΦΟΡΙΚΗ ΚΙΝΗΣΗ;

ή και ΜΟΝΟ για τη ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ ;

Η απάντηση

Ας μελετήσουμε το φαινόμενο ΚΥΛΙΣΗ ΜΙΑΣ ΜΠΙΛΙΑΣ ΣΕ ΚΕΚΛΙΜΕΝΟ ΕΠΙΠΕΔΟ

Κατά την εξέλιξη του φαινομένου ΚΥΛΙΣΗ καθεμιά από τις ασκούμενες δυνάμεις έχει τις ιδιαιτερότητές της.

Η mgημφ είναι συνιστώσα της διατηρητικής mg και η Τ είναι στατική τριβή, δύναμη δηλαδή που δεν εργάζεται

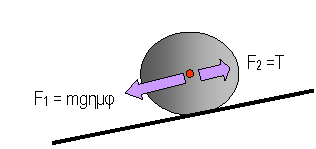Όταν αναλύουμε την κύλιση σε μεταφορική και στροφική κίνηση και

μελετάμε τη ΜΕΤΑΦΟΡΙΚΗ κίνηση δεχόμαστε ότι η επιτάχυνση και η ταχύτητα του κέντρου μάζας άρα και η κινητική ενέργεια του σώματος διαμορφώνονται όχι από τις συγκεκριμένες δυνάμεις mgημφ και Τ αλλά ΑΠΟ ΔΥΟ ΔΥΝΑΜΕΙΣ F₁ και F₂ Η ΜΙΑ ΑΠΟ ΤΙΣ ΟΠΟΙΕΣ, η F1, ΕΙΝΑΙ ΙΣΗ ΜΕ ΤΗΝ mgημφ και η άλλη, η F₂, ΕΙΝΑΙ ΙΣΗ με την Τ αλλά ΔΕΝ ΕΙΝΑΙ ΣΤΑΤΙΚΗ ΤΡΙΒΗ.

Υπό αυτή την έννοια η κινητική ενέργεια του σώματος στη μεταφορική αυτή κίνηση αποκτά τιμή ΙΣΗ με εκείνη που ΘΑ αποκτούσε ένα σώμα μάζας m στο κέντρο μάζας του οποίου θα δρούσαν δύο δυνάμεις αντίθετης κατεύθυνσης η μία, η F₁, ΙΣΗ με την mgημφ και η άλλη μία δύναμη F₂ με ΕΡΓΟ ΑΡΝΗΤΙΚΟ, ΙΣΗ με την Τ, η οποία όμως ΔΕΝ ΕΙΝΑΙ ΣΤΑΤΙΚΗ ΤΡΙΒΗ

Κατά τη ΜΕΤΑΦΟΡΙΚΗ κίνηση .

½mυc_m² = mgh_cm - Τx

η ΣΤΡΟΦΙΚΗ κίνηση περί άξονα που περνάει από το κέντρο μάζας είναι αυτή που θα διέκρινε ένας παρατηρητής σε μεταφορικά κινούμενο σύστημα αναφοράς με την ταχύτητα και την επιτάχυνση του κέντρου μάζας. Κατά την εξέλιξη του φαινομένου, η αύξηση της κινητικής ενέργειας του σώματος είναι ίση με το έργο της ροπής ζεύγους F₃, F₄ καθεμιά από τις δυνάμεις του οποίου είναι ίση με την Τ.

Και η Τ κατά τη περιστροφή αυτή δεν είναι «στατική τριβή»

Κατά τη ΣΤΡΟΦΙΚΗ κίνηση

½I_cmω² = Τx