
Θέματα, απαντήσεις λύσεις , εκτιμήσεις
ΘΕΜΑ 1ο
Στις
ερωτήσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το
γράμμα που αντιστοιχεί στη σωστή απάντηση.
1. Λέγοντας "το φως έχει διπλή φύση" εννοούμε
ότι:
α. απορροφάται και εκπέμπεται
β. αλληλεπιδρά με θετικά και αρνητικά φορτισμένα
σωματίδια
γ., συμπεριφέρεται ως κύμα και ως
σωματίδιο
δ. είναι συνδυασμός ηλεκτρικού και μαγνητικού
κύματος. Μονάδες
5
2. Σε μια εξώθερμη
πυρηνική αντίδραση:
α. η συνολική μάζα ηρεμίας των προϊόντων είναι
ίση με τη συνολική μάζα ηρεμίας των αντιδρώντων
β. η ενέργεια Q της
αντίδρασης είναι θετική
γ. η ενέργεια Q της αντίδρασης είναι αρνητική
δ. δεν
ισχύει ο νόμος της διατήρησης του συνολικού αριθμού των νουκλεονίων. Μονάδες 5
3. Ο Rutherford κατά το βομβαρδισμό
λεπτού φύλλου χρυσού με σωμάτια α παρατήρησε ότι:
α. κανένα
σωμάτιο α δεν εκτρέπεται από την πορεία του
β. όλα τα σωμάτια α εκτρέπονται κατά 180°
γ. λίγα σωμάτια α εκτρέπονται κατά 180°
δ. τα
σωμάτια α έχουν αρνητικό φορτίο. Μονάδες
5
4. Σύμφωνα με την κβαντική
θεωρία του Planck,
κάθε άτομο εκπέμπει ή απορροφά στοιχειώδη ποσά ενέργειας, που ονομάζονται:
α. φωτόνια β. ηλεκτρόνια
γ.
ποζιτρόνια δ. νετρόνια Μονάδες 5
Μια παρατήρηση.
Σύμφωνα με την κβαντική θεωρία η εκπομπή (και η
απορρόφηση) ακτινοβολίας
α. περιγραφόμενη
σε μια ορισμένη γλώσσα λαμβάνει χώρα έτσι ώστε η αντίστοιχη ενέργεια
να είναι ακέραιο πολλαπλάσιο ενός στοιχειώδους ποσού, που ονομάζεται quantum (ΚΒΑΝΤΟ) ενέργειας.
β. σε
μια άλλη γλώσσα περιγράφεται ως εκπομπή
(ή απορρόφηση) σωματιδίων τα
οποία ονομάζονται ΦΩΤΟΝΙΑ.
Το φωτόνιο είναι ΣΩΜΑΤΙΔΙΟ με μηδενικό φορτίο, με μάζα ηρεμίας
μηδενική, είναι το σωματίδιο μεσολαβητής
της ηλεκτρομαγνητικής αλληλεπίδρασης, είναι σωματίδιο με spin 1, είναι το «διασημότερο» από τα
μποζόνια και εν πάση περιπτώσει ΦΕΡΕΙ
ΣΤΟΙΧΕΙΩΔΕΣ ΠΟΣΟ ΕΝΕΡΓΕΙΑΣ (ενός κβάντου) , ΔΕΝ ΕΙΝΑΙ ΤΟ ΣΤΟΙΧΕΙΩΔΕΣ ΠΟΣΟ ΕΝΕΡΓΕΙΑΣ.
Μολονότι η θεώρηση αυτή
δεν πρόκειται να επηρεάσει τις επιδόσεις των μαθητών, όσοι δηλαδή μαθητές απαντήσουν θα υποστηρίξουν ότι είναι « η σωστή απάντηση είναι το φωτόνιο»
καταθέτουμε την άποψη μας διότι είναι πιστεύουμε αναγκαία – και για εμάς τους
φυσικούς αλλά και για τους διδακτικούς μας στόχους- η σημασιακή διάκριση της έννοιας ΣΩΜΑΤΙΔΙΟ από την
έννοια ΕΝΕΡΓΕΙΑ την οποία φέρει.
5.
Να γράψετε στο τετράδιό σας το γράμμα της πρότασης και δίπλα τη λέξη που την συμπληρώνει
σωστά.
α. Η διαδικασία της συνένωσης δυο ελαφρών
πυρήνων για να σχηματίσουν ένα βαρύτερο, λέγεται πυρηνική . . . . . . . ΣΥΝΤΗΞΗ
β. Όσο μεγαλύτερη είναι η ενέργεια σύνδεσης ανά
νουκλεόνιο τόσο . . . . . . . είναι ο
πυρήνας. ΣΤΑΘΕΡΟΤΕΡΟΣ
γ. Κατά τη διάσπαση β-
(βήτα πλην) εκπέμπεται από τον πυρήνα .
. . . . . και αντινετρίνο. ΗΛΕΚΤΡΟΝΙΟ
δ. Τα μήκη κύματος των ακτίνων Χ είναι πολύ. . . .
. . από τα μήκη κύματος των ορατών ακτινοβολιών. ΜΙΚΡΟΤΕΡΑ
ε. Ατομικός αριθμός είναι ο αριθμός των . . . . . του πυρήνα. ΠΡΩΤΟΝΙΩΝ Μονάδες 5
ΘΕΜΑ 20
1. Ερευνητής χειρίζεται συσκευή παραγωγής
ακτίνων Χ και επιθυμεί να αυξήσει τη διεισδυτικότητά τους. Πώς θα πρέπει να
μεταβάλει την τάση μεταξύ ανόδου-καθόδου της συσκευής;
α. Να την αυξήσει. β. Να την ελαττώσει.
Μονάδες
2
Να δικαιολογήσετε
την απάντησή σας. Μονάδες
5
α. Η κινητική ενέργεια κάθε
ηλεκτρονίου που «φθάνει» στην άνοδο είναι ανάλογη προς την τάση .
(Ο
συλλογισμός βασίζεται στον Νόμο Διατήρησης της ενέργειας).
β. Η κινητική ενέργεια ενός ηλεκτρονίου που «φθάνει» στην άνοδο είναι
ΙΣΗ με την ενέργεια ενός φωτονίου Χ
μέγιστης ενέργειας. Αυτό συμβαίνει στην
περίπτωση που, μετά την «γέννηση» του
φωτονίου, η κινητική ενέργεια που
«απέμεινε» στο ηλεκτρόνιο είναι
μηδενική.
(Ο
συλλογισμός βασίζεται στον Νόμο Διατήρησης της ενέργειας)
γ. Όσο μεγαλύτερη είναι η ενέργεια των
φωτονίων τόσο πιο διεισδυτική είναι η ακτινοβολία Χ.
(Γνώση ως
πληροφορία)
δ. Όσο μεγαλύτερη είναι η τάση τόσο
πιο διεισδυτική θα είναι η ακτινοβολία
Συμπέρασμα
που απορρέει από την σύνθεση των παραπάνω)
Μια πιο φορμαλιστική προσέγγιση την οποία - εικάζω ότι - θα
συναντήσουμε στα περισσότερα από τα γραπτά των μαθητών είναι η προτεινόμενη από
την Κεντρική Επιτροπή. Σύμφωνα με αυτήν:
α. Οι
ακτίνες Χ που έχουν μικρά μήκη κύματος είναι περισσότερο διεισδυτικές.
(Γνώση ως
πληροφορία)
β. Με βάση τη
σχέση λmin
= ch/ eV
πρέπει να αυξήσουμε την τάση.
(
Απομνημόνευση ενός «τύπου». Συλλογισμός )
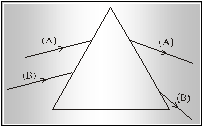
2. Δυο παράλληλες ακτίνες
μονοχρωματικού φωτός (Α) και (Β) προσπίπτουν σε πρίσμα και εκτρέπονται, όπως
φαίνεται στο σχήμα. Ποια ακτίνα φωτός έχει το μεγαλύτερο μήκος κύματος;
α. Η
ακτίνα Α.
β. Η ακτίνα Β.
Μονάδες 2
Να δικαιολογήσετε
την απάντησή σας.
Μονάδες 5
α. Οι ακτίνες με το μεγαλύτερο μήκος κύματος
υφίστανται μικρότερη εκτροπή
( Γνώση
αποθηκευμένη στη μνήμη είτε ως διατύπωση, είτε – στην καλύτερη περίπτωση- ως
εικόνα με τις ερυθρά ακτινοβολία να εκτρέπεται λιγότερο σε συνδυασμό με την αποθηκευμένη γνώση ότι η ερυθρά ακτινοβολία έχει το
μεγαλύτερο μήκος κύματος)
β. Από το σχήμα διαπιστώνεται
ότι η εκτροπή της Α είναι συγκριτικά μικρότερη
( Κατανόηση της
έννοιας «εκτροπή από πρίσμα» )
3. Να μεταφέρετε στο
τετράδιό σας συμπληρωμένες τις παρακάτω πυρηνικές αντιδράσεις:
![]()
![]() Μονάδες
4
Μονάδες
4
4.
Το παρακάτω σχήμα παριστά την καμπύλη διάσπασης για ένα
δείγμα ραδιενεργού στοιχείου. Ο χρόνος υποδιπλασιασμού του στοιχείου αυτού
είναι:
α. 7s β. 10,5s γ. 3,5s Μονάδες 2
Να δικαιολογήσετε
την απάντησή σας. Μονάδες
5
Από το σχήμα φαίνεται ότι σε χρόνο 7s ο αριθμός των αδιάσπαστων πυρήνων
υποτετραπλασιάστηκε. Άρα η προτεινόμενη τιμή 7s δεν είναι ο χρόνος υποδιπλασιασμού. Φαίνεται επίσης και η τιμή 10,5s
δεν μπορεί να είναι ο χρόνος υποδιπλασιασμού. Κατά συνέπεια ο
ζητούμενος χρόνος είναι το 3,5s.
(Ο συλλογισμός βασίζεται σε σωστή ανάγνωση του διαγράμματος
και σε γνώση της έννοιας χρόνος
υποδιπλασιασμού )
ΘΕΜΑ
3ο
Ακτίνα ορατής μονοχρωματικής
ακτινοβολίας συχνότητας 6·1014Hz, διέρχεται από τον αέρα σε γυάλινη πλάκα. Ο δείκτης διάθλασης του γυαλιού
για την παραπάνω ακτινοβολία είναι 1,5.
1. Να
υπολογίσετε το μήκος κύματος της ακτινοβολίας λ0 στο κενό. Μονάδες 6
2. Να υπολογίσετε την ταχύτητα διάδοσης της
ακτινοβολίας μέσα στο γυαλί. Μονάδες
6
3. Να υπολογίσετε το μήκος κύματος της
ακτινοβολίας λ μέσα στο γυαλί. Μονάδες
6
4. Να βρείτε πόσο διαφέρει η ενέργεια ενός
φωτονίου της ακτινοβολίας στο κενό από την ενέργεια του φωτονίου αυτού, όταν η
ακτίνα βρίσκεται μέσα στο γυαλί. Μονάδες
7
Δίνονται: η
ταχύτητα του φωτός στο κενό c0=3·108m/s
1.
Συμβολίζουμε με το γράμμα f
τη συχνότητα της ακτινοβολίας. Εφαρμόζουμε τη θεμελιώδη εξίσωση των κυμάτων για
τη διάδοση της ακτινοβολίας στο κενό c0= λ0f, από την οποία λ0=c0/f. Αντικαθιστώντας στο S.I. λ0=
5.10-7 m.
2.
Συμβολίζουμε με το γράμμα c
την ταχύτητα της ακτινοβολίας στο γυαλί και με το γράμμα n τον δείκτη διάθλασης του γυαλιού. Σύμφωνα με
την εξίσωση ορισμού του δείκτη διάθλασης του γυαλιού ισχύει n = c0/c με συνέπεια c=c0/n. Αντικαθιστώντας στο S.I. c=2.108 m/s.
3.Εφαρμόζουμε
τη θεμελιώδη εξίσωση των κυμάτων για τη διάδοση της ακτινοβολίας στο γυαλί c= λf, από την οποία λ=c/f. Αντικαθιστώντας στο S.I. λ=
3,33.10-7 m.
(Πρέπει να γίνει αποδεκτή και η λύση βασιζόμενη στη εξίσωση n = λ0/λ, μολονότι η εξίσωση αυτή δεν θα έπρεπε να ανήκει
σε εκείνες που οφείλουν να
απομνημονεύουν και να χρησιμοποιούν χωρίς απόδειξη οι μαθητές μας)
4. Η
ενέργεια ενός φωτονίου εξαρτάται μόνο από τη συχνότητα της ακτινοβολίας. Η
συχνότητα μιας ακτινοβολίας έχει την ίδια τιμή είτε διαδίδεται στο κενό είτε σε
οποιοδήποτε άλλο μέσο. Η τιμή της ενέργειας κάθε φωτονίου της ακτινοβολίας
παραμένει αναλλοίωτη οπουδήποτε και αν διαδίδεται η ακτινοβολία
Και ορισμένες ΠΑΡΑΤΗΡΗΣΕΙΣ:
Α. Με το 3ο αυτό ΘΕΜΑ
αξιολογούμε το κατά πόσον οι μαθητές μας
α. είναι σε θέση να χρησιμοποιούν
τη θεμελιώδη εξίσωση των κυμάτων
β. είναι σε θέση να
χρησιμοποιούν την εξίσωση ορισμού του δείκτη διάθλασης,
γ. γνωρίζουν τη σχέση της ενέργειας κάθε φωτονίου με τη συχνότητα,
δ. έχουν αντιληφθεί ότι η
συχνότητα μιας ακτινοβολίας αποτελεί το βασικό στοιχείο της ταυτότητάς της και
δεν μεταβάλλεται κατά τη διάδοσή της σε οποιοδήποτε μέσο.
Γ.
Κατά την άποψή μας ΚΡΙΝΕΤΑΙ ΩΣ ΙΔΙΑΙΤΕΡΑ ΘΕΤΙΚΟ το ότι κατά τη διατύπωση του
θέματος δεν δόθηκαν τα (περισσότερα από)
τα σύμβολα των μεγεθών.
Η διατύπωση δηλαδή
ήταν «ακτινοβολία συχνότητας 6·1014Hz» και όχι «ακτινοβολία συχνότητας f=6·1014Hz». Η πρακτική αυτή πρέπει
να επεκταθεί στο σύνολο των διατυπώσεων με στόχο να αντιμετωπιστεί η
φροντιστηριακή θεώρηση ότι ΣΥΧΝΟΤΗΤΑ ΕΙΝΑΙ
ΤΟ f, η συχνότητα είναι δηλαδή είναι κάτι το οποίο δεν είναι
αναγκαίο να το κατανοήσεις, αρκεί να ξέρεις ότι είναι f, ώστε να μπορείς να το βάζεις στον κατάλληλο «τύπο».
Γ. Το
θέμα αυτό ίσως επηρεάσει τη διδασκαλία των συναδέλφων στο να ΑΝΑΔΕΙΚΝΥΟΥΝ ΤΗΝ
ΙΔΙΑΙΤΕΡΗ ΣΗΜΑΣΙΑ ΤΗΣ ΕΝΝΟΙΑΣ ΣΥΧΝΟΤΗΤΑ ΩΣ ΘΕΜΕΛΙΑΚΟ ΣΤΟΙΧΕΙΟ ΤΑΥΤΟΤΗΤΑΣ ΜΙΑΣ
ΑΚΤΙΝΟΒΟΛΙΑΣ και να περιορίσουν τον ρόλο της έννοιας ΜΗΚΟΣ ΚΥΜΑΤΟΣ. Και αυτό
-προκειμένου για την προσέγγιση των διδακτικών στόχων- θα ήταν θετικό.
Δ. Η
κοινότητα των φυσικών πρέπει επιτέλους να αντισταθεί στην σχεδόν εδραιωμένη
φροντιστηριακή αντίληψη για τη διδασκαλία
και ως πρώτη ενέργεια να επιβάλει την άποψη για τον ΠΕΡΙΟΡΙΣΜΟ ΤΩΝ
ΕΞΙΣΩΣΕΩΝ , όπως η λ= λ0/n, ΤΙΣ ΟΠΟΙΕΣ ΟΦΕΙΛΕΙ ΝΑ
ΑΠΟΜΝΗΜΟΝΕΥΕΙ Ο ΜΑΘΗΤΗΣ.
ΘΕΜΑ 4ο
Κινούμενο ηλεκτρόνιο
συγκρούεται με ακίνητο άτομο υδρογόνου, το οποίο βρίσκεται στη θεμελιώδη
κατάσταση με ενέργεια Ε1=–13,6 eV. Η κινητική ενέργεια του ηλεκτρονίου πριν
από την κρούση είναι 16,12eV.
Το άτομο του υδρογόνου απορροφά μέρος της ενέργειας του προσπίπτοντος ηλεκτρονίου,
διεγείρεται στη δεύτερη διεγερμένη στάθμη (n=3) και εξακολουθεί να παραμένει ακίνητο
μετά την κρούση.
1. Να σχεδιάσετε στο τετράδιό σας σε διάγραμμα
ενεργειακών σταθμών όλες τις δυνατές μεταβάσεις από τη διεγερμένη κατάσταση (n=3) στη θεμελιώδη κατάσταση. Μονάδες
4
2. Να υπολογίσετε το μήκος κύματος του φωτονίου
που εκπέμπεται κατά την αποδιέγερση του ατόμου από την κατάσταση n=3 στην κατάσταση n=2 .
Μονάδες
6
3. Να υπολογίσετε το ποσοστό (επί τοις εκατό) της
κινητικής ενέργειας του προσπίπτοντος ηλεκτρονίου που απορροφήθηκε από το άτομο
του υδρογόνου κατά την κρούση.
Μονάδες 7
4. Να υπολογίσετε την κινητική ενέργεια και το
μέτρο της στροφορμής του ηλεκτρονίου του ατόμου του υδρογόνου στη διεγερμένη
κατάσταση n=3.
Μονάδες 8
Δίνονται: η ταχύτητα του φωτός στο κενό c0=3·108m/s
η σταθερά του Planck, h=6,6·10-34J·s
1eV=1,6·10-19J
και π=3,14.
Κάποιες απαντήσεις
2. Συμβολίζουμε με λ το
ζητούμενο μήκος κύματος και με f
αντίστοιχη συχνότητα. Η ενέργεια του ηλεκτρονίου στη δεύτερη διεγερμένη στάθμη είναι ίση με Ε1/9 και
στην πρώτη Ε1/4 . Κατά την
αποδιέγερση ενός ηλεκτρονίου και την σύγχρονη εκπομπή ενός φωτονίου ενέργειας hf, σύμφωνα με τη διατήρηση της
ενέργειας, ισχύει Ε1/9 -Ε1/4 = hf. Σύμφωνα με τη θεμελιώδη εξίσωση των κυμάτων c=λf άρα και λ =c/f. Από τις εξισώσεις αυτές υπολογίζεται το
ζητούμενο μήκος κύματος λ = hc0/
Ε1/9 -Ε1/4.
Αντικαθιστώντας στο S.I. λ = 6,55.10-7 m.
3. Η ενέργεια που
απορρόφησε το άτομο από το προσπίπτον ηλεκτρόνιο είναι ίση με τη διαφορά Ε1/9
-Ε1 . Αντικαθιστώντας στο S.I. η τιμή της είναι 12,09 eV .
Η ενέργεια την οποία είχε το προσπίπτον ηλεκτρόνιο δίδεται ίση με 16,12 eV .
Μ ε απλή μέθοδο βρίσκουμε ότι το ποσοστό της ενέργειας που απορροφήθηκε είναι
75%.
4 α. ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ
του ηλεκτρονίου στη διεγερμένη
κατάσταση n=3.
Εφαρμόζουμε σε ένα
περιφερόμενο ηλεκτρόνιο τον δεύτερο
νόμο του Newton,
τον νόμο του Coulomb για την αλληλεπίδρασή
του με το φορτίο του πυρήνα, χρησιμοποιούμε την εξίσωση για την κεντρομόλο
επιτάχυνσή του και την εξίσωση K=
½mυ2
για την κινητική του ενέργεια και καταλήγουμε στη σχέση Κ= kce2/2R.
Χρησιμοποιούμε την
εξίσωση ορισμού της έννοιας δυναμικό και την εξίσωση για την τιμή του
δυναμικού ενός ηλεκτρικού πεδίου Coulomb
και, για την τιμή της δυναμικής ενέργειας προκύπτει
U = - kce2/R, οπότε η ενέργεια του ηλεκτρονίου ως
άθροισμα U
+ K
θα είναι ίση με - kce2/2R.
Διαπιστώνουμε ότι η
τιμή της κινητικής ενέργειας είναι αντίθετη από την τιμή της (ολικής) ενέργειας
του ηλεκτρονίου. Εφόσον η ενέργεια του ηλεκτρονίου στην δεύτερη διεγερμένη
κατάσταση είναι ίση με Ε1/9 = - 1,51 eV , η ενέργεια του ηλεκτρονίου θα είναι ίση
με 1,51 eV
.
β. Η ΣΤΡΟΦΟΡΜΗ του
ηλεκτρονίου στη διεγερμένη κατάσταση n=3.
Συμβολίζουμε τη
ζητούμενη στροφορμή με το γράμμα L.
Σύμφωνα με τη θεωρία του Niels
Bohr για το μοντέλο του υδρογόνου, η στροφορμή
του ηλεκτρονίου λόγω της περιφοράς παίρνει ΜΟΝΟ τις τιμές που είναι ακέραια
πολλαπλάσια του h
/2π. Η τιμή της για κάθε κατάσταση
δίνεται από τη σχέση L= n h /2π
όπου n
ο αντίστοιχος κύριος κβαντικός αριθμός. Συνεπώς για την διεγερμένη κατάσταση με
n
=3 θα είναι L=
3 h
/2π. Αντικαθιστώντας στο S.I. έχουμε L= 3,2 Js.
Μια
εικασία. Ερώτημα εύκολο . . . . μικρό Βατερλώ
Κατά την
προσωπική μας εκτίμηση το ερώτημα για την τιμή της στροφορμής θα αποτελέσει ένα
μικρό Βατερλώ για τους υποψηφίους, μολονότι πρόκειται για ένα σχετικά απλό
ερώτημα.
(Η ζητούμενη τιμή της στροφορμής υπολογίζεται
μόνο με την τιμή της σταθεράς του
Πλανκ) .
Η πρόβλεψή μας
αυτή βασίζεται στον «τρόπο» με τον οποίο
το γνωστικό αυτό αντικείμενο
παρουσιάζεται στο σχολικό εγχειρίδιο και στη φυσιολογικά συνεπαγόμενη
χαμηλή ποιότητα της διδασκαλίας του από τους εκπαιδευτικούς.
1. Πουθενά δεν
παρουσιάζεται η σχέση L=
n
h/2π η οποία συνδέει «άμεσα» τη στροφορμή με τη σταθερά του Planck. Αντίθετα παρουσιάζεται ως μία σχέση
«κρυμμένη» πίσω από τις L
= mυr και mυr = n
h/2π.
2. Εμφανίζεται
δηλαδή ως περίπου κρυμμένη η σχέση που θα μπορούσε να οδηγήσει τον διδάσκοντα
να πει -στους νεαρούς μαθητές του και στις νεαρές μαθήτριές του- ότι «η μικρότερη στροφορμή (λόγω περιφοράς)
είναι «η σταθερά του Πλανκ δια 2π» και ότι
Η ΤΙΜΗ ΑΥΤΗ ΕΙΝΑΙ ΜΙΑ ΠΑΓΚΟΣΜΙΑ ΣΤΑΘΕΡΑ
3. Η ποσότητα mυr ( μάζα ηλεκτρονίου επί ταχύτητα ηλεκτρονίου επί
ακτίνα τροχιάς ) εμφανίζεται επίμονα και στις δύο σχετικές εξισώσεις γεγονός
που ωθεί τον εξεταζόμενο να αναζητήσει
τον υπολογισμό της στροφορμής στο γινόμενο mυr. Η αναζήτηση αυτή της τιμής της στροφορμής στο
γινόμενο mυr ενισχύεται στους μαθητές της θετικής και
της τεχνολογικής κατεύθυνσης οι οποίοι διδάχθηκαν τη στροφορμή υλικού σημείου
σε κυκλική τροχιά ως προς το κέντρο του κύκλου ως μέγεθος με μέτρο το γινόμενο mυr.
4. Στην
παρουσίαση της κβάντωσης της στροφορμής, ο
αριθμός n
παρουσιάζεται ως n = 1, 2, 3, . . . . . ∞
, στην καλύτερη δηλαδή ανάγνωση ως ένας ακέραιος θετικός αριθμός, χωρίς πουθενά να αναφέρεται έστω και
υπαινικτικά ότι ο αριθμός αυτός είναι ( σύμφωνα με το μοντέλο του Bohr) ο κύριος κβαντικός αριθμός, ο
οποίος θα κάνει την εμφάνισή του αργότερα , με το ίδιο σύμβολο (n),
ως αριθμός η τιμή του οποίου θα καθορίσει τις επιτρεπόμενες τροχιές και
τις επιτρεπόμενες τιμές ενέργειας. Πουθενά δηλαδή δεν γίνεται κάποια αναφορά
στο θεωρητικό δεδομένο ότι «για κάθε ενεργειακή στάθμη με κβαντικό αριθμό 1, 2,
3, . . . . οι αντίστοιχες τιμές στροφορμής θα είναι h/2π,
2h/2π, 3h/2π. . . .» , όπως αυτό επισημαίνεται κατά την
παρουσίαση των επιτρεπόμενων τιμών ακτίνας και ενέργειας.
Εξυπακούεται ότι
όλα τα παραπάνω συνιστούν βέβαια μια προσωπική άποψη για τον τρόπο παρουσίασης
της στροφορμής στο μοντέλο του Bohr
αλλά η εικασία για τις επιδόσεις των εξεταζομένων δεν συνιστά τίποτα
περισσότερο από μία εικασία. Η βαθμολόγηση των γραπτών και η σχετική
έρευνα θα αποδείξουν ότι η υπόθεση ήταν
βάσιμη ή και ότι δεν ήταν βάσιμη. Εξάλλου δεν είναι και λίγες οι περιπτώσεις
που πέσαμε όλοι μας έξω όταν θελήσαμε να προβλέψουμε, κατά μέσον όρο, τις επιδόσεις των δεκάδων χιλιάδων μαθητών.
Ανδρέας
Ιωάννου Κασσέτας