Ανδρέας Ιωάννου Κασσέτας

Τεράστιο, πολύχρωμο, στημένο όρθιο στον ουρανό, τόξο γεωμετρικό, άψογο, χαραγμένο λες με αόρατο διαβήτη,

τα χρώματα στην ίδια πάντα σειρά, εμφανίζεται από το πουθενά, άγγελος απαγγέλλων το τέλος της καταιγίδας, εξάγγελος επερχόμενης γαλήνης, ένα τόξο «θαύμα» ουρανού, ίσως το πιο εντυπωσιακό που αντίκρισε και αντικρίζει η ανθρώπινη όραση, είναι φυσικό να μας αφήνει έκθαμβους όλους και όχι μόνο τον Νώε, τον Καρτέσιο και τον Διονύση Σαββόπουλο.

«γιατί» ένα τέτοιο τεράστιο τόξο κάνει ξαφνικά την εμφάνισή του στον ουρανό;

Το «γιατί» το «τόξο με τα χρώματα» εμφανίζεται στον ουρανό , αίνιγμα πανάρχαιο, απασχόλησε ιδιαίτερα τους Άραβες στοχαστές του Μεσαίωνα αλλά μια πειστική απάντηση ήταν αδύνατον να δοθεί δεδομένου ότι έλειπαν δύο τουλάχιστον στοιχεία .

Το ένα ήταν ο νόμος για το φαινόμενο διάθλαση, στον οποίο έφθασαν οι Ολλανδοί – ο Snell - και ο Descartes - Καρτέσιος τον 17ο αιώνα

και το άλλο μια θεωρία για το φως και τα χρώματα σαν αυτή που πρότεινε ο Νεύτων λίγες δεκαετίες αργότερα.

Εκείνος που πλησίασε περισσότερο την απάντηση για το τι συμβαίνει

ήταν ο Καρτέσιος.

Γοητευμένος από το ΟΥΡΑΝΙΟ ΤΟΞΟ,

διέθετε τον νόμο της διάθλασης

αλλά του έλειπε η νευτωνική θεωρία για τα χρώματα .

Στο Discours de la Methode,

το 1637 απέδωσε εύστοχα το φαινόμενο

στη διάθλαση του ηλιακού φωτός

στα αιωρούμενα μετά τη βροχή σταγονίδια,

υπέθεσε ότι το μέγεθος των σταγόνων φωτός δεν επηρεάζει την εμφάνισή του

και – το σημαντικότερο – έκανε ο ίδιος ΠΕΙΡΑΜΑ

με τη διάθλαση ηλιακού φωτός σε μια μεγάλη γυάλινη σφαίρα γεμάτη με νερό. Μετρώντας τις γωνίες με βάση τον νόμο της διάθλασης, έφθασε στο αποδεκτό σήμερα συμπέρασμα ότι το βασικό ουράνιο τόξο ήταν συνέπεια μιας ανάκλασης στο εσωτερικό των σφαιρικών σταγόνων και το δευτερεύον συνέπεια δύο ανακλάσεων στο εσωτερικό των σταγόνων. Με βάση πάντα τον νόμο της διάθλασης υπολόγισε και το ύψος στο οποίο κάνει την εμφάνισή του. Οι ερμηνείες, όμως τις οποίες πρότεινε για τα χρώματα ήταν ελάχιστα πειστικές διότι δεν διέθετε τη νευτωνική θεωρία.

Η Οπτική του Νεύτωνα πρόσφερε σοβαρές βελτιώσεις στην ερμηνεία του φαινομένου βασιζόμενες στο ότι η μπλε ακτινοβολία «λυγίζει» περισσότερο από την κόκκινη.

Η οικοδόμηση μιας ολοκληρωμένης ερμηνείας συνεχίστηκε τον 19ο αιώνα μετά την παρέμβαση και του Thomas Young o οποίος υποστήριξε ότι το φως είναι κυματική οντότητα με μήκος κύματος κάτι ο Νεύτων το είχε αρνηθεί.

Τον 20ο αιώνα η σύγχρονη ερμηνεία εμπλουτίστηκε με την θεωρία του Gustav Mie

για τη σκέδαση του φωτός σε σωματίδια .

Οι εξηγήσεις των φυσικών δεν είναι τόσο εύκολο να κατανοηθούν. Χρειάζεται κανείς να ξέρει Γεωμετρία και τον νόμο της διάθλασης. Μελετούν τη διαδρομή μιας φωτεινής ακτίνας σε ένα σταγονίδιο βροχής το οποίο θεωρούν σφαιρικό. Ξέρουν ότι ο δείκτης διάθλασης του νερού για τις διάφορες ακτινοβολίες είναι γύρω στο 1,33

Στο μοντέλο που προτείνουν, ας παρακολουθήσουμε τη διαδρομή μιας μονοχρωματικής ακτίνας,

ας πούμε μιας πράσινης, όταν πέσει σε μια διάφανη ΣΦΑΙΡΑ με δείκτη διάθλασης 1,337

Η κάθετος στην επιφάνεια μιας σφαίρας είναι μια ευθεία που κατευθύνεται στο κέντρο της

Ας υποθέσουμε ότι η οριζόντια διαδιδόμενη στον άερα πράσινη πέφτει με γωνία 6Ο⁰. Κατά ένα μέρος ανακλάται και κατά ένα μέρος ΔΙΑΘΛΑΤΑΙ, σύμφωνα με τον νόμο, με γωνία θ₁ = 40, 37⁰. Ας παρακολουθήσουμε την ποσότητα που διαθλάστηκε.

Ταξιδεύει μέσα στη σφαίρα και πέφτει στη διαχωριστική επιφάνεια με γωνία και πάλι – σύμφωνα με τη Γεωμετρία- ίση με θ₂ = 40, 37⁰ , οπότε κατά ένα μέρος ΑΝΑΚΛΑΤΑΙ και κατά ένα μέρος διαθλάται. Ας παρακολουθήσουμε την ανακλώμενη. Συνεχίζει να ταξιδεύει μέσα στη σφαίρα και πέφτει στη διαχωριστική επιφάνεια με γωνία και πάλι ίση με θ₄ = 40, 37⁰ , οπότε κατά ένα μέρος ανακλάται και κατά ένα μέρος ΔΙΑΘΛΑΤΑΙ. Ας παρακολουθήσουμε την ποσότητα που ΔΙΑΘΛΑΣΤΗΚΕ και βγήκε στον αέρα.

Η γωνία με την οποία εξέρχεται είναι -σύμφωνα με τον νόμο του Snell - ίση με 60⁰. Οι γωνίες θ₁,θ₂,θ₃,θ₄ είναι ίσιες μεταξύ τους και η συνολική «στροφή» της πράσινης ακτίνας είναι περίπου 138,5⁰. Το αντίστοιχο φως φθάνει σε ανθρώπινο μάτι ως μία διαφορετική δέσμη πράσινη .

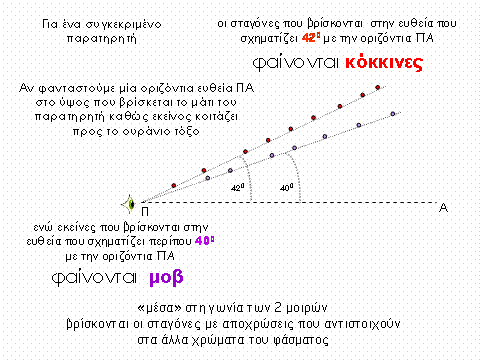
Για μία κόκκινη ακτίνα, η οποία πέφτει στο ίδιο σημείο με την πράσινη υπό γωνία επίσης 60⁰, μετά από μία ανάλογη περιπέτεια μέσα στη σφαιρική στανόνα υπολογίζεται ότι εξέρχεται μετά από συνολική στροφή 138⁰. Το αντίστοιχο φως φθάνει σε ανθρώπινο μάτι ως μία διαφορετική δέσμη κόκκινη που σχηματίζει με τον ορίζοντα γωνία 42⁰.

Ενδιαφερόμαστε με ανάλογο τρόπο για τη διαδρομή της μπλε συνιστώσας ακτινοβολίας κατά την πρόσπτωση υπό γωνία θ₁ = 60⁰ και διαπιστώνουμε θεωρητικά ότι εξέρχεται από τη σταγόνα με συνολική εκτροπή 140⁰ .

Το αντίστοιχο φως φθάνει σε ανθρώπινο μάτι ως μία διαφορετική δέσμη μπλε υπό γωνία 40⁰ ως προς τον ορίζοντα

Ανάλογη διαδρομή έχουν και οι άλλες ακτινοβολίες-χρώματα, η πορτοκαλί, η κίτρινη, η ιώδης .

Η επιλογή της γωνίας πρόσπτωσης των 60⁰ γίνεται διότι για την τιμή αυτή γωνίας πρόσπτωσης παρατηρείται η μεγαλύτερη εκτροπή συγκριτικά με οποιαδήποτε άλλη γωνία πρόσπτωσης.

Σχηματίζεται όμως και ένα δεύτερο, ασθενέστερο, ουράνιο τόξο στο οποίο τα χρώματα είναι

σε αντίθετη διάταξη, κάτω δηλαδή το κόκκινο και ψηλότερα από όλα το μενεξεδί

Το δευτερεύον ουράνιο τόξο σχηματίζεται από τις ακτίνες που εξέρχονται, αφού υποστούν δύο εσωτερικές ανακλάσεις Σε αυτή την περίπτωση αποδεικνύεται ότι οι εξερχόμενες ερυθρές ακτίνες σχηματίζουν 51⁰ με τον ορίζοντα, ενώ οι ιώδεις σχηματίζουν 54,5⁰. Αυτό σημαίνει ότι ο σταγόνες που φαίνονται κόκκινες είναι κάτω από τις αντίστοιχες ιώδεις.

Επιστροφή στην πρώτη σελίδα με τα περιεχόμενα