Πανελλήνιες εξετάσεις στη Φυσική κατεύθυνσης

Ημερήσιου Γενικού Λυκείου. 2012

Θέμα Α

Α1. το σωστό είναι το γ

Α2. το σωστό είναι το β

Α3. το σωστό είναι το γ

Α4. το σωστό είναι το γ

Α5.

α. Σωστό β. Σωστό

γ Λάθος

δ. Λάθος ε. Σωστό

Θέμα Β

Β.1 Ακτίνα μονοχρωματικού φωτός προερχόμενη από πηγή που βρίσκεται μέσα 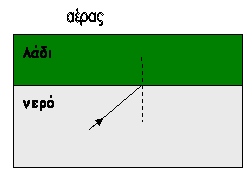στο νερό προσπίπτει στη διαχωριστική επιφάνεια νερού-αέρα υπό γωνία ίση με την κρίσιμη. Στην επιφάνεια του νερού ρίχνουμε στρώμα λαδιού το οποίο δεν αναμειγνύεται με το νερό, έχει πυκνότητα μικρότερη από το νερό και δείκτη διάθλασης μεγαλύτερο από τον δείκτη διάθλασης του νερού . Τότε η ακτίνα α. θα εξέλθει στον αέρα β. θα υποστεί ολική ανάκλαση γ. θα κινηθεί παράλληλα προς τη διαχωριστική γραμμή λαδιού-αέρα.

Να επιλέξετε τη σωστή πρόταση ( μονάδες 2 )

Να δικαιολογήσετε την επιλογή σας ( μονάδες 6)

Σχόλιο : Η διατύπωση σε ορισμένους μαθητές ίσως προκαλέσει σύγχυση. Θα προτιμούσαμε τη διατύπωση :

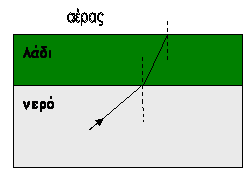
Ένα στρώμα λαδιού επιπλέει στην επιφάνεια του νερού και πάνω από το λάδι - όπως φαίνεται στο σχήμα- υπάρχει αέρας. Μια ακτίνα μονοχρωματικού φωτός προερχόμενη από φωτεινή πηγή που βρίσκεται στο νερό , όπως στο σχήμα , προσπίπτει στη διαχωριστική επιφάνεια νερού – λαδιού υπό γωνία πρόπτωσης θ. Αν η τιμή της θ είναι ίση με την κρίσιμη γωνία του συστήματος «νερό – αέρας» η φωτεινή ακτίνα α. θα εξέλθει στον αέρα

β. θα υποστεί ολική ανάκλαση γ. θα βρεθεί στη διαχωριστική γραμμή λαδιού-αέρα.

Μια λύση

Φυσική . Γενικά : Κατά τη διάθλαση του φωτός από ένα διαφανές μέσο ( όπως το νερό ή το λάδι ) στον αέρα η μέγιστη γωνία πρόσπτωσης θ_cr για την οποία γίνεται διάθλαση λέγεται κρίσιμη γωνία του διόπτρου «διαφανές μέσο- αέρας» και αντιστοιχεί σε γωνία διάθλασης οριακά ίση με 90 μοίρες. Βάσει του νόμου του Snell ισχύει nημθ_κρ = n_αέρα ημ90⁰ και επειδή ο δείκτης διάθλασης του αέρα θεωρείται ίσος με 1, ημθ_cr = 1/n

Σχετικά με το συγκεκριμένο φαινόμενο :

Εφόσον η γωνία πρόπτωσης – ας τη θεωρήσουμε θ₁ - είναι ίση με την κρίσιμη γωνία του συστήματος «νερό αέρας» ισχύει n_νερού ημθ₁ = 1 (1)

Για το φαινόμενο «διάθλαση» στη διαχωριστική επιφάνεια του νερού λαδιού - αν γωνία διάθλασης είναι θ₂ -ισχύει

n_νερού ημθ₁ = n_λαδιού ημθ₂ (2)

Από τις (1) και (2) προκύπτει ημθ₂= 1/n_λαδιού (3)

Η φωτεινή ακτίνα προσπίπτει στη διαχωριστική επιφάνεια λαδιού υπό γωνία πρόπτωσης έστω θ₃

Γεωμετρία . Οι γωνίες θ₂ και θ₃ είναι εντός εναλλάξ άρα θ₂ = θ₃

οπότε η σχέση (3) γίνεται ημθ₃ = 1/n_λαδιού

Η γωνία πρόπτωσης θ₃ στη διαχωριστική επιφάνεια λαδιού αέρα είναι συνεπώς ίση με την ορική γωνία του συστήματος λάδι-αέρας, άρα το φως θα εξέλθει οριακά, υπό γωνία 90^{0 ,}θ, θα βρίσκεται δηλαδή σχεδόν πάνω στη διαχωριστική επιφάνεια λαδιού αέρας .

Β2. Σε γραμμικό ελαστικό μέσο, κατά μήκος του ημιάξονα Οx,δημιουργείται στάσιμο κύμα με κοιλία στη θέση x=0. Δύο σημεία Κ και Λ του ελαστικού μέσου βρίσκονται αριστερά και δεξιά του πρώτου δεσμού, μετά τη θέση x=0, σε αποστάσεις λ/6 και λ/12 από αυτόν αντίστοιχα, όπου λ το μήκος κύματος των κυμάτων που δημιουργούν το στάσιμο κύμα . Ο λόγος των μέγιστων ταχυτήτων υ_Κ/υ_Λ των σημείων αυτών είναι α. √3 β. 1/3 γ. 3

Μια λύση

Γενικά : Ας υποθέσουμε ότι έχουμε ένα στάσιμο κύμα ως αποτέλεσμα της συμβολής δύο τρεχόντων κυμάτων με ίσα πλάτη Α και ίσες συχνότητες f τα οποία διαδίδονται στο ίδιο γραμμικό ελαστικό μέσο σε κατευθύνσεις αντίθετες και συμβάλλουν.

Αν θεωρήσουμε χωρικό σύστημα αναφοράς με άξονα x να συμπίπτει με την ευθεία του γραμμικού ελαστικού μέσου και με την αρχή των αξόνων Ο να βρίσκεται στη θέση ισορροπίας μιας κοιλίας, αποδεικνύεται ότι η ταλάντωση ενός υλικού σημείου με θέση ισορροπίας στον θετικό ημιάξονα και στην τετμημένη x θα έχει πλάτος ίσο με 2Α|συν 2πx/λ|, από όπου αποδεικνύεται και ότι η απόσταση της θέσης ισορροπίας μιας κοιλίας από τον γειτονικό δεσμό είναι ίση με λ/4 .

Στο συγκεκριμένο ερώτημα .

Η μέγιστη ταχύτητα για έναν ταλαντωτή είναι ίση με το γινόμενο της γωνιακής συχνότητας επί το πλάτος

Άρα για τους ταλαντωτές Κ και Λ ο λόγος των μέγιστων ταχυτήτων θα είναι ίση με τον λόγο των αντίστοιχων πλατών

Η θέση ισορροπίας του υλικού σημείου Κ απέχει από τη θέση ισορροπίας της κοιλίας λ/4 - λ/6 = λ/12.

ενώ η αντίστοιχη απόσταση για το Λ είναι λ/4 + λ/12 = λ/3.

Το πλάτος ταλάντωσης του Κ θα είναι 2Α|συν 2πx_Κ/λ| . Με x_Κ= λ/12 το πλάτος γίνεται 2Α|συνπ/6| = Α√3

Το πλάτος ταλάντωσης του Λ θα είναι 2Α|συν 2πx_Λ/λ|. Με x_Λ= λ/12 το πλάτος γίνεται ίσο με 2Α|συν 2π/3| = Α.

Ο λόγος των πλατών είναι συνεπώς ίσος με √3, άρα και ο λόγος των μέγιστων ταχυτήτων είναι επίσης ίσος με √3.

Σχόλιο.

Τι ακριβώς αξιολογούμε με ένα τέτοιο ερώτημα ;

α. Το να γνωρίζει ο διδασκόμενος ότι η απόσταση δεσμού κοιλίας είναι λ/4

β. Το να « ξέρει απέξω» τη συνάρτηση για το πλάτος ταλάντωσης Α’ = 2Α|συν 2πx/λ|

γ. Το να θυμάται ότι σε μια αρμονική ταλάντωση το πλάτος είναι ίσο με το γινόμενο « ω Α»

δ. Το να μπορεί να διαχειριστεί αλγεβρικά τις μαθηματικές αυτές δομές.

Ίσως θα έπρεπε να ξανακοιτάξουμε το «τι ακριβώς επιδιώκουμε με τη διδασκαλία της Φυσικής»

Β3. Ανάμεσα σε δύο παράλληλους τοίχους ΑΓ και ΒΔ υπάρχει λείο οριζόντιο επίπεδο. Τα ευθύγραμμα τμήματα ΑΒ και ΓΔ είναι κάθετα στους τοίχους. Σφαίρα Σ₁ κινείται πάνω στο δάπεδο, με σταθερή ταχύτητα, μέτρου υ, παράλληλη προς τους τοίχους και καλύπτει τη διαδρομή από το ΑΒ μέχρι το ΓΔ σε χρόνο t₁. Στη συνέχεια δεύτερη σφαίρα Σ₂

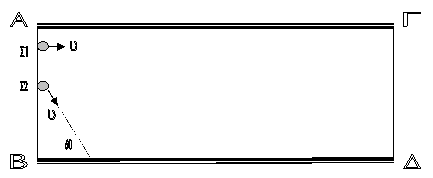που έχει ταχύτητα μέτρου υ συγκρούεται ελαστικά με τον ένα τοίχο υπό γωνία φ= 60⁰ και μετά από διαδοχικές ελαστικές κρούσεις με τους τοίχους, καλύπτει τη διαδρομή από το ΑΒ μέχρι το ΓΔ σε χρόνο t₂. Οι σφαίρες εκτελούν μόνο μεταφορική κίνηση. Τότε θα ισχύει : α. t₂ = 2t₁.

β . t₂ = 4t₁ = 4t₂. γ. t₂ = 8t₁.

Να επιλέξετε τη σωστή απάντηση ( μονάδες 2 )

Να δικαιολογήσετε την επιλογή σας ( μονάδες 7 )

Δίνονται ημ60⁰ = √3/2 συν60⁰ = ½

Σχόλιο :

Έπρεπε να αναφέρεται και ότι :

Η ακτίνα κάθε σφαίρας να θεωρηθεί αμελητέα σε σχέση με τις διαστάσεις του ΑΓΔΒ .

Το σύνολο των χρονικών διαστημάτων των κρούσεων να θεωρηθεί αμελητέο σε σχέση με τους χρόνους t₁ και t₂.

Έπρεπε επίσης να αναφέρεται ότι

Η τροχιά της Σ₂ σχηματίζει γωνία 60⁰ με τον τοίχο ΒΔ, πριν πέσει σε αυτόν. και όχι

«συγκρούεται ελαστικά με τον ένα τοίχο υπό γωνία φ= 60⁰ »

Μια λύση

Για την ευθύγραμμη ομαλή κίνηση της Σ₁ ισχύει 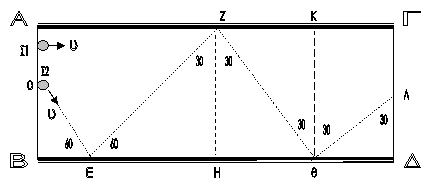t₁ = d/υ, όπου d η απόσταση των παραλλήλων ΑΒ και ΓΔ

Η οποιαδήποτε κρούση της Σ₂ με τοίχωμα θεωρείται ελαστική άρα η κινητική ενέργεια της Σ₂ διατηρείται σταθερή και με την κρούση δεν αλλοιώνεται το μέτρο της ταχύτητας ενώ η γωνία πρόσπτωσης είναι σε κάθε περίπτωση γωνία 30⁰ και ίση με τη γωνία ανάκλασης.

Για την κίνηση της Σ₂ από την αρχική θέση μέχρι το σημείο Ε της πρώτης πρόσκρουσης

ο χρόνος κίνησης είναι ίσος με ΟΕ/υ .

Η Γεωμετρία. Στο τρίγωνο ΟΒΕ η γωνία είναι 30^ο άρα η υποτείνουσα ΟΕ είναι διπλάσια της πλευράς ΒΕ.

Για τη διαδρομή ΕΖ, η απόσταση ΕΖ είναι επίσης ως υποτείνουσα του τριγώνου διπλάσια από την ΕΗ.

Και αυτό ισχύει και για τις υπόλοιπες διαδρομές. Καθεμιά τους ως μήκος υποτείνουσας τριγώνου με γωνία 30 είναι ΔΙΠΛΑΣΙΑ από την αντίστοιχη κάθετη πλευρά.

t₂ = (OE)/υ + (ΕΖ)/υ + ( ΖΘ)/υ + (ΘΛ)/υ

t₂ = 2(ΒΕ)/υ + 2(ΕΗ)/υ + 2(ΗΘ)/υ + 2(ΘΔ)/υ

t₂ = 2(ΒΕ+ ΕΗ+ ΗΘ+ ΘΔ)/υ

Αυτό θα συμβαίνει οσεσδήποτε και να είναι οι κρούσεις διότι σε κάθε διαδρομή ανάμεσα σε δύο κρούσεις,

η διανυόμενη απόσταση θα είναι διπλάσια από την αντίστοιχη κάθετη προβολή της στην ΒΔ

t₂ = 2d/υ t₂ = 2t₁

θέμα Γ

Ομογενής και ισοπαχής δοκός (ΟΑ) μάζας Μ = 6 kg και μήκους ℓ =0,3 m, μπορεί να στρέφεται χωρίς τριβές σε κατακόρυφο επίπεδο γύρω από οριζόντιο άξονα που περνά από το ένα άκρο της Ο. Στο άλλο της άκρο Α υπάρχει στερεωμένη μικρή σφαίρα μάζας m = M/2 .

Γ₁. Βρείτε τη ροπή αδράνειας του συστήματος δοκού – σφαίρας ως προς τον άξονα περιστροφής του. (Μονάδες 6)

Σχόλιο

Έπρεπε να αναφέρεται ότι η ακτίνα της σφαίρας είναι -σε σχέση με το μήκος της ράβδου- ασήμαντη

Μια λύση

Η ως προς τον άξονα (Ο) ροπή αδράνειας του συστήματος δοκού σφαίρας είναι άθροισμα της ως προς Ο ροπής αδράνειας της «μικρής» σφαίρας, mℓ² και της ως προς Ο ροπής αδράνειας της αδράνειας της ράβδου, η οποία, σύμφωνα με το θεώρημα Steiner είναι Ι_cm + M(ℓ/2)² =1/12Mℓ² + Mℓ²/4 =1/3Mℓ² Τελικά Ι_ο = 1/3Mℓ²+ mℓ² mκαι εφόσον m = M/2

Ι_ο = 5/6Mℓ² Ι_ο = 0,45 kgm².

Ασκούμε στο άκρο Α δύναμη σταθερού μέτρου F = 120/π Ν , που είναι συνεχώς κάθετη στη δοκό όπως φαίνεται στο σχήμα.

Γ₂. Βρείτε το έργο της δύναμης F κατά την περιστροφή του συστήματος μέχρι την οριζόντια θέση της ράβδου (Μονάδες 6)

Εφόσον η ροπή της F είναι σταθερή, το έργο της δύναμης F ( λέγεται και «έργο σταθερής ροπής ) είναι ίσο με το γινόμενο «ροπή δύναμης επί γωνία στροφής»

W_F = Fℓπ/2 W_F = 18 J.

ή εφόσον η ασκούμενη δύναμη έχει σταθερό μέτρο και εφάπτεται στην τροχιά του σημείου στο οποίο ασκείται το έργο της είναι ίσο με το γινόμενη «δύναμη επί μήκος τόξου γωνίας 90 μοιρών » W_F = F. 2πℓ/4 W_F = 18 J.

Γ₃. Βρείτε τη γωνιακή ταχύτητα του συστήματος δοκού-σφαίρας στην οριζόντια θέση. (Μονάδες 6)

Σχόλιο

Έπρεπε να αναφέρεται ότι το σύστημα ράβδος- σφαίρα είναι αρχικά ακίνητο.

Μια λύση

Εφαρμόζουμε το θεώρημα έργου – ενέργειας στο σύστημα δοκός– σφαίρα από την αρχική θέση με τη ράβδο κατακόρυφη ακίνητη , στην τελική θέση με τη ράβδο οριζόντια

½ Ι_οω² – 0 = W_F + W_Mg + W_mg

Το έργο της δύναμης «βάρος δοκού» είναι αρνητικό και ίσο με W_Mg = - Μgℓ /2 . W_Mg = - 9 J

ο έργο της δύναμης «βάρος σφαίρας» είναι επίσης αρνητικό και ίσο με W_mg = - mgℓ W_mg = - 9 J

Με βάση τα παραπάνω ½ Ι_οω² = 0 . Τη στιγμή, δηλαδή, που η ράβδος γίνεται οριζόντια η κινητική της ενέργεια άρα και η γωνιακή της ταχύτητα είναι μηδέν .

Επαναφέρουμε το σύστημα δοκού σφαίρας στην αρχική κατακόρυφο θέση του . Ασκούμε στο άκρο Α δύναμη, σταθερού μέτρου F’ = 30 √3 N, που είναι συνεχώς κάθετη στη δοκό.

Γ₄. Βρείτε τη γωνία που σχηματίζει η δοκός με την κατακόρυφο τη στιγμή που η κινητική της ενέργεια γίνεται μέγιστη. (Μονάδες 6)

Δίνονται : g = 10m/s² , I_cm = 1/12 Mℓ² ημ60⁰ = συν30⁰ = √3/2

ημ30⁰ = συν 60⁰ = ½

Σχόλιο

Η διατύπωση του ερωτήματος όφειλε να είναι διαφορετική . Ένα παράδειγμα διαφορετικής διατύπωσης :

Γ4. Κατά την στροφική κίνηση του αρχικά ακίνητου συστήματος κατά γωνία π/2, από τη στιγμή που η ράβδος είναι οριζόντια μέχρι να γίνει κατακόρυφη, σε κάποια στιγμή της κίνησης η κινητική ενέργεια του συστήματος έχει τη μεγαλύτερη τιμή σε σχέση με όλες τις άλλες θέσεις . Να προσδιορίσετε τη γωνία που σχηματίζει η δοκός με την κατακόρυφο τη στιγμή εκείνη;

Μια λύση με βάση τη δική μας διατύπωση

Η πρώτη σκέψη είναι, βασιζόμενοι στο θεώρημα έργου ενέργειας, να δημιουργήσουμε μια συνάρτηση κινητικής ενέργειας και γωνιακής μετατόπισης θ (θ <π/2) . Η συνάρτηση είναι η Κ = F’ℓθ + Mgℓσυνθ - Mgℓ και ομολογουμένως πολύ δύσκολα οδηγεί σε κάποιο συμπέρασμα.

Μάλιστα για ένα μαθητή η συνάρτηση δεν οδηγεί πουθενά.

Η επόμενη σκέψη είναι να διακρίνουμε την εξέλιξη της κινητικής ενέργειας με βάση την εξέλιξη της στροφορμής ή της ολικής ροπής , η οποία, σύμφωνα με τον νόμο είναι ίση με τον «ρυθμό μεταβολής της στροφορμής» . Εφαρμόζουμε τον νόμο για τη στροφική κίνηση, σε κάποια στιγμή που η ράβδος έχει διαγράψει γωνία θ < π/2 . Θεωρούμε άξονα z κάθετο στο επίπεδο του σχήματος με θετική φορά προς τα έξω. Η ροπή του ολικού βάρους είναι αρνητική ενώ η ροπή της F είναι θετική . Αν η ροπή της F έχει απόλυτη τιμή μεγαλύτερη από εκείνη του βάρους η ολική ροπή είναι θετική, άρα σύμφωνα με τον νόμο για τη στροφική κίνηση ( τ_ολ = dL/dt ) η στροφορμή αυξάνεται. Η ροπή της F είναι σταθερή ενώ η ροπή του βάρους καθώς το κέντρο μάζας ανέρχεται συνεχώς (σε απόλυτη τιμή) αυξάνεται. Σε κάποια στιγμή της στροφικής κίνησης η ολική ροπή γίνεται μηδέν και μετά η ολική ροπή γίνεται αρνητική, άρα η στροφορμή ελαττώνεται, συνεπώς και η γωνιακή ταχύτητα και η κινητική ενέργεια. Στο χρονικό διάστημα που η στρεφόμενη ράβδος διαγράφει τη γωνία των 90 μοιρών σε κάποια στιγμή κατά την οποία η ολική ροπή είναι μηδέν. Τη στιγμή εκείνη το στρεφόμενο σύστημα έχει τη μεγαλύτερη στροφορμή ( άρα και τη μεγαλύτερη κινητική ενέργεια ) σε σχέση με τις υπόλοιπες στιγμές της στροφικής αυτής κίνησης των 90 μοιρών . Αν η γωνία της ράβδου με την κατακόρυφο τη στιγμή εκείνη είναι θ, ( θ< π/2) για την τιμή της ολικής ροπής ισχύει : τ_ολ = dL/dt = Fℓ - Mgℓ/2 ημφ – mgℓ ημφ

Άρα dL/dt = 0 ( και τ_ολ = 0 ) εφόσον Fℓ - Mg ℓ/2 ημφ– mgℓ ημφ =0

ημφ = F/ (Mg/2 + mg) ημφ = F/ (Mg/2 + mg) ημφ = √3/2 √3/2 φ = π/3.

Τώρα έτσι όπως είναι η διατύπωση δημιουργείται πρόβλημα αρκετά σοβαρό δεδομένου ότι δεν αναφέρεται εάν το ζητούμενο μέγιστο αναζητείται κατά την κίνηση μέχρι γωνιακή μετατόπιση π/2 .

Ήταν μια σοβαρή αβλεψία αλλά έχω επίγνωση ότι τα θέματα των εξετάσεων διαμορφώνονται από ανθρώπους και οι άνθρωποι κάνουν οπωσδήποτε και λάθη.

Είναι εξάλλου βέβαιο ότι στο συγκεκριμένο κείμενο ΕΧΩ κάνει κάποια λάθη.

Και είναι γεγονός ότι οι χιλιάδες φυσικοί στα βαθμολογικά κέντρα (εξεταστές φυσικώς αδυνάτων) – εξ όσων γνωρίζω όλοι ανεξαιρέτως - διέκριναν τον «υπαινιγμό» ότι δηλαδή το ζητούμενο αναφέρεται σε κίνηση στο πρώτο τεταρτημόριο. Εξάλλου ο Πικάσσο ήταν αυτός που έγραψε ότι είναι πολύ ανθρώπινο το ότι οι άνθρωποι δεν βλέπουν «αυτό που βλέπουν», αλλά βλέπουν «αυτό που ξέρουν» .

Μια άποψη για την ακύρωση

Το πρόβλημα που δημιουργήθηκε αντιμετωπίστηκε από την Επιτροπή με την ακύρωση του θέματος Γ₄. Εκτιμώ ότι δεν είναι η καλύτερη δυνατή αντιμετώπιση. Από τη μια επιχειρείται να περιοριστεί η ενδεχόμενη αδικία σε μαθητές που δραστηριοποιήθηκαν σε μια γενικότερη κατεύθυνση χάνοντας πολύτιμο χρόνο, αλλά από την άλλη αδικεί τους πολύ περισσότερους μαθητές οι οποίοι, κινούμενοι στη λογική της διατύπωσης που κάναμε , το αντιμετώπισαν με επιτυχία.

Πολύ δύσκολα ακόμα και μια έρευνα στα γραπτά - η οποία βέβαια δεν θα γίνει ποτέ –

θα μπορούσε να δείξει

πόσοι μαθητές «ταλαιπωρήθηκαν» από την έλλειψη κάποιας αναφοράς σε «ζητούμενο πρώτο μέγιστο» και

πόσοι ήταν οι μαθητές οι οποίοι τα κατάφεραν και με την λύση της ακύρωσης αδικούνται.

Όταν λοιπόν λείπει η έρευνα εκείνο που μπορεί να κάνει κανείς για να πάρει μια θέση σε ένα κοινωνικό πρόβλημα είναι να «αφουγκράζεται». Και προσωπικά πιστεύω ότι η μεγάλη πλειοψηφία των εκπαιδευτικών της πράξης αφουγκράζεται ότι η επιλογή της Επιτροπής θα προκαλέσει πολύ περισσότερη αδικία - αλλοιώνοντας κατάφωρα τη σειρά - από όση ενδεχομένως συντελέστηκε.

Με πιο απλά λόγια η επιλογή της Επιτροπής να ακυρώσει το θέμα δεν έδωσε ΛΥΣΗ στο προβλήματος το οποίο δημιουργήθηκε από μια αβλεψία της. Ήταν μια «δύσκολη» κοινωνική άσκηση την οποία η Επιτροπή των εξετάσεων όχι μόνο δεν έλυσε αλλά την περιέπλεξε χειρότερα. Θέλω να πιστεύω ότι τα μέλη της Επιτροπής που ήταν και καθηγητές Φυσικής στη Δευτεροβάθμια δύσκολα αποδέχτηκαν την επιλογή της ακύρωσης.

Ένα σχόλιο.

Η δοκός, ένα δοκάρι της πραγματικότητας και η «μικρή» σφαίρα των 380 κυβικών

Τα μοντέλα και η Πραγματικότητα

Η ΔΟΚΟΣ που προτείνεται στο θέμα Γ είναι ένα μοντέλο στερεού σώματος με ιδιαίτερο στοιχείο το ότι οι δύο από τις τρεις διαστάσεις -που έχει ως πραγματικό δοκάρι της Πραγματικότητας- θεωρούνται αμελητέες . Δεν ξέρω αν αυτός που πρότεινε δοκό μιας διάστασης, την φαντάστηκε ξύλινη ή σιδηροδοκό. Ούτως ή άλλως όμως η μάζα της δοκού 6 kg, εντυπωσιακή. Δοκός με μάζα 6 kg, μήκος 30 cm και τις οι άλλες διαστάσεις ασήμαντες είναι – για τα δρομάκια της Πραγματικότητας – αρκετά δύσκολο. Αν είναι σιδηροδοκός το εμβαδόν διατομής θα είναι γύρω στα 25 cm² και διαστάσεις 5cm X 5 cm αυθαδιάζουν στο μοντέλο «διαστάσεις αμελητέες». Για μια ράβδο 30 cm οι άλλες διαστάσεις 5cm X 5 cm είναι δύσκολο να θεωρηθούν ασήμαντες.

Αν τη δοκό την φαντάστηκαν ξύλινη και όταν λέμε δοκό, και όχι σιδηροδοκό, συνήθως εννοούμε δοκάρι ξύλινο - τα πράγματα γίνονται πολύ δύσκολα, το μοντέλο γραμμική ράβδος αναπνέει δύσκολα. Γιατί σε τέτοια περίπτωση το ξύλινο δοκάρι μήκους 30 cm έχει εμβαδόν διατομής γύρω στα 250 cm² άρα οι δύο «αμελητέες» διαστάσεις είναι περίπου 16cm x 16 cm και όταν είσαι 16 εκατοστά δεν μπορούν να σε πουν «αμελητέα διάσταση» σε σχέση με τη διάσταση 30 εκατοστών της ράβδου.

Τα πράγματα αγριεύουν ακόμα περισσότερο με τον άλλο πρωταγωνιστή του θέματος Γ, την λεγόμενη «μικρή» σφαίρα τη στερεωμένη στο άκρο της ράβδου. Η «μικρή» αυτή σφαίρα έχει μάζα 3 kg ( !) , άρα ακόμα κι αν είναι σιδερένια θα έχει όγκο γύρω στα 380 κυβικά ή μιλιλίτρ όπως λένε οι χημικοί. Αυτό σημαίνει ότι και ατσάλινο να είναι η σφαίρα θα έχει διάμετρο γύρω στα 9 cm. Σε μια δοκό μήκους 30 cm μια «μικρή» σφαίρα με διάμετρο 9 cm όχι μόνο δεν είναι μικρή αλλά υπονομεύει και τη Φυσική που χρησιμοποιήσαμε γιατί το κέντρο μάζας δεν απέχει 30 cm από τον άξονα περιστροφής, με όλες τις συνέπειες, από την τιμή της ροπής αδράνειας μέχρι το μήκος του τόξου που διαγράφει το κέντρο μάζας της «μικρής» σφαίρας .

Τα μοντέλα δεν είναι μόνο αναγκαία, συνιστούν το αναπνευστικό σύστημα της Φυσικής.

Χωρίς αυτά ο γάμος της ΕΜΠΕΙΡΙΑΣ με τα ΜΑΘΗΜΑΤΙΚΑ δεν θα γινόταν ποτέ και αυτό σημαίνει ότι «καμία Φυσική δεν θα είχε γεννηθεί».

Οφείλουμε ωστόσο να έχουμε επίγνωση ότι τα μοντέλα δεν είναι η Πραγματικότητα αλλά «προσεγγίζουν» την Πραγματικότητα.

Θέμα Δ

Λείο κεκλιμένο επίπεδο έχει γωνία κλίσης 30^ο . Στα σημεία Α και Β στερεώνουμε τα άκρα δύο ιδανικών ελατηρίων με σταθερές k₁ = 60 N/m και k₂ = 140 N/m αντίστοιχα. Στα ελεύθερα άκρα των ελατηρίων 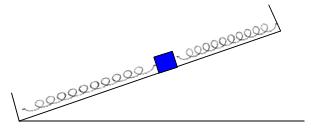δένουμε ένα σώμα Σ₁ μάζας m 1 = 2 kg και το κρατάμε στη θέση όπου τα ελατήρια έχουν το φυσικό τους μήκος ( όπως φαίνεται στο σχήμα ). Τη χρονική στιγμή to = 0 αφήνουμε το σώμα Σ₁ ελεύθερο.

Δ₁ . Να αποδείξετε ότι το σώμα Σ₁ θα εκτελέσει απλή αρμονική ταλάντωση. ( μονάδες 5 )

Μια λύση .

Προσδιορίζουμε τη θέση ισορροπίας του ταλαντωτή . Είναι εκείνη στην οποία η συνισταμένη των ασκουμένων δυνάμεων είναι μηδέν. Οι ασκούμενες στο σώμα δυνάμεις είναι βάρος, κάθετη δύναμη και δύναμη από τα δύο ελατήρια. Στη θέση αυτή το ελατήριο k₁ σπρώχνει, ενώ το άλλο ελατήριο τραβά. και Θεωρώντας την επιμήκυνση του ενός ίση με δ, η ελάττωση μήκους του άλλου θα είναι επίσης ίση με δ .

Αναλύοντας σε άξονα x παράλληλο προς την επιφάνεια του κεκλιμένου και y κάθετον στον x,

έχουμε ΣF _x = 0 k₁ δ + k₂ δ - m₁ gημθ ( 1 ) άρα δ = m₁ gημθ/(k₁ + k₂) δ = 5 cm.

H θέση ισορροπίας απέχει από το σημείο αφήσαμε το σώμα Σ₁ με μηδενική ταχύτητα.

Θεωρούμε το κινούμενο αντικείμενο σε τυχαία στιγμή της κίνησης κατά την οποία η απομάκρυνση να είναι x

Η συνισταμένη των ασκουμένων στο σώμα δυνάμεων έχει αλγεβρική τιμή κατά τον άξονα x ( με θετικά προς τα κάτω )

ίση με F = -mgημθ - k₁( δ+x) – k₂ (δ + x) και λόγω της ( 1) F = - (k₁ +k₂ ) x.

Η συνάρτηση ανάμεσα σε F και x στην οποία καταλήγουμε αποδεικνύει ότι η κίνηση είναι αρμονική ταλάντωση.

Δ₂. Να γράψετε τη σχέση που δίνει την απομάκρυνση του σώματος Σ₁ από τη θέση ισορροπίας σε συνάρτηση με τον χρόνο . Να θεωρήσετε θετική φορά από το Α προς το Β. ( μονάδες 7 )

Η ζητούμενη συνάρτηση έχει γενικά τη μορφή x = Αημ(ωt+φ) . Για να τη συγκροτήσουμε χρειαζόμαστε α. το πλάτος β. τη γωνιακή συχνότητα ω και γ. την αρχική φάση φ.

Εφόσον το Σ₁ αφήνεται στη θέση στην οποία τα ελατήρια έχουν το φυσικό τους μήκος η απόσταση (δ = 5cm) της θέσης αυτής από τη θέση ισορροπίας είναι ίση με το πλάτος της ταλάντωσης.

Εφόσον κατά την ταλάντωση αυτή ισχύει F = - (k₁ +k₂ ) x, το άθροισμα (k₁ +k₂ )είναι η σταθερά της ταλάντωσης ίση με το γινόμενο m₁ω². k₁ +k₂ = - m₁ω² ω²=(k₁ +k₂ )/m₁ . ω= 100 rad/s

Αν στη συνάρτηση θέσουμε t = 0 θα έχουμε τη θέση ( απομάκρυνση ) του σώματος στην αρχή των χρόνων. Η θέση αυτή είναι, σύμφωνα με την επιλογή της αρχής των χρόνων η θέση για την οποία x_a = + A

A = Αημφ ημφ =1 φ =π/2 x = 0,05 ημ(10t+π/2)

Κάποια χρονική στιγμή που το σώμα Σ₁ βρίσκεται στην αρχική του θέση , τοποθετούμε πάνω του

(χωρίς αρχική ταχύτητα ) ένα άλλο σώμα Σ₂ μικρών διαστάσεων , μάζας m₂ = 6 kg. Το σώμα Σ₂ δεν ολισθαίνει πάνω στο σώμα Σ₁ λόγω της τριβής που δέχεται από αυτό. Το σύστημα των δύο σωμάτων κάνει απλή αρμονική ταλάντωση.

Δ₃. Να βρείτε τη σταθερά επαναφοράς της ταλάντωσης του σώματος Σ₂. ( μονάδες 6 ) x

Η σταθερά επαναφοράς D του Σ₂ μπορεί να προσδιοριστεί από το γινόμενο D = m₂ ω² (1)

Αποδείξαμε ότι κατά την ταλάντωση του Σ1 με τα δύο ελατήρια ισχύει F = - (k₁ +k₂ ) x.

Άρα σε οποιαδήποτε ταλάντωση με δύο ελατήρια όπως αυτή που μελετήσαμε η σταθερά επαναφοράς είναι ίση με k₁ +k₂ , ανεξάρτητα από τη μάζα του ταλαντωτή.

Όταν εκτελεί ταλάντωση με τα ίδια ελατήρια το σύστημα των Σ₁ και Σ₂ η σταθερά επαναφοράς θα είναι

k₁ +k₂ και ίση με (m₁ +m₂) ω² k₁ +k₂ = (m₁ +m₂) ω² (2)

Από τις (1) και (2) προκύπτει D = (k₁ +k₂)m₂ /(m₁ +m₂) D = 150 Ν/m

Δ₄. Να βρείτε τον ελάχιστο συντελεστή οριακής τριβής που πρέπει να υπάρχει μεταξύ των σωμάτων Σ₁ και Σ₂, ώστε το Σ₂ να μην ολισθαίνει σε σχέση με το Σ₁.

Δίνονται ημ60⁰ = συν30⁰ = √3/2 g = 10m/s²

Θεωρώ τον άξονα x με θετικά από B προς A

Σε μια τυχαία θέση «κάτω» από τη θέση ισορροπίας για την κίνηση του Σ₂ ισχύει

m₁gημθ - Τ_σ = - Dx ( x >0 ) Τ_σ = m₂gημθ + Dx

Από τη συνάρτηση Τ_σ = f(x ) φαίνεται καθαρά ότι καθώς το σώμα Σ₂ κινείται σε ταλάντωση προς τα κάτω η τιμή της στατικής τριβής αυξάνεται και ότι η μεγαλύτερη τιμή είναι Τ_σ = m₂gημθ + DΑ₂ ( 3) ( Α₂ το πλάτος )

Με τρόπο αντίστοιχο με τον προηγούμενο προσδιορίζουμε το πλάτος της ταλάντωσης του Σ₂

ΣF _x = 0 k₁ Α₂ + k₂ Α₂ - (m₁ +m₂) gημθ Α₂ = 20 cm

H μεγαλύτερη τιμή της στατικής τριβής κατά την εξέλιξη της ταλάντωσης είναι συνεπώς

σύμφωνα με την (3) Τ_σ = 60 Ν

Για να διατηρείται όμως το Σ₂ πάνω στο Σ₁ και να μην ολισθαίνει, πρέπει η μεγαλύτερη τιμή να είναι μικρότερη ή ίση από το γινόμενο μ_σΝ₂ όπου μ_σ ο συντελεστής στατικής τριβής. Το Ν₂ παριστάνει την κάθετη δύναμη που ασκεί το Σ₁ στο Σ₂ και είναι ίση με m₂gσυνφ

Τ_σ ≤μ_σΝ₂ μ_σ ≥ 2√3/3

Η τιμή της στατικής τριβής στη θέση ισορροπίας είναι ίση με m₂gημθ = 15Ν

Αν το σώμα κινείται προς τα πάνω η τιμή της στατικής τριβής μειώνεται γίνεται μικρότερη από 15 Ν. Στο άκρο της ταλάντωσης η δύναμη επαναφοράς αποδεικνύεται ίση με 30 N, άρα η στατική τριβή είναι ίση με μηδέν

Τα μοντέλα και η Πραγματικότητα. Συμπλήρωμα.

Το βιβλίο του Στέλιου του Ράμφου που διαβάζω αυτή την εποχή «Η λογική της παράνοιας» έχει 400 σελίδες και ζυγίζει αρκετά όταν το κρατάς στο χέρι . Όταν πρόσεξα πόσο βαριά είναι το προτεινόμενα αντικείμενα και στο θέμα Δ το έβαλα στη ζυγαριά για να διαπιστώσω ότι η παγκόσμια έλξη που του ασκεί η Γη είναι 7 περίπου νιούτον, η μάζα του είναι 700 περίπου γραμμάρια.

Το αντικείμενα του θέματος Δ στα οποία εφαρμόζουμε νόμους της Μηχανικής του υλικού σημείου θεωρούνται αμελητέων διαστάσεων σε σχέση με τις διαστάσεις των ελατηρίων. Και τα δύο θεωρούνται υλικά σημεία και η τροχιά καθενός είναι μια ευθεία γραμμή χωρίς να γίνεται κάποια έμμεση έστω αναφορά στην έννοια κέντρο μάζας ή κάποια νύξη ότι η κίνησή τους είναι μεταφορική κίνηση σώματος με διαστάσεις. Ωστόσο το ένα από αυτά, το κάτω, είναι 2 kg, σε μάζα περίπου όσο τρία βιβλία του Ράμφου. Όσο για το άλλο αυτό είναι 6 kg όσο εννέα βιβλία, το καθένα 400 σελίδων. Δεν μπορώ να υποθέσω πώς έχουν φανταστεί ένα τέτοιο αντικείμενο οι προτείνοντες το 6 κιλά . Το πιθανότερο είναι να είναι κάτι μεταλλικό

Υπάρχει και η τιμή του συντελεστή στατικής τριβής η οποία σύμφωνα με τη Φυσική υπολογίστηκε 2√3/3 λίγο, δηλαδή, περισσότερο από 1,15.

Χρειάζεται ίσως να θυμίσουμε ότι η συντριπτική πλειοψηφία των ζευγαριών των υλικών παρουσιάζει συντελεστή στατικής τριβής κατά κανόνα μικρότερο. Ειδικά για τα μέταλλα, μετρήσεις με κεκλιμένα επίπεδα έχουν δώσει τιμές όπως ατσάλι με ατσάλι 0,61, γυαλί με χαλκό 0, 65, μαντέμι με ψευδάργυρο 0,85, μπρούντζος με ατσάλι 0,51, ασήμι με ασήμι 0,5 . . .Δύσκολα βρίσκεις συντελεστή στατικής τριβής ίσο με 1, 15 αν και εμφανίζονται συχνά εμφανίζονται σημαντικές διαφορές για το ίδιο ζευγάρι.

Αν εξαιρέσουμε το λάστιχο γιατί λάστιχο με μάζα 6 κιλά θα είχε τεράστιο όγκο, ένα ζευγάρι με μεγάλο συντελεστή τριβής είναι το όπως το αλουμίνιο – αλουμίνιο με συντελεστή τριβής από 1,Ο5 έως 1,3. Αλλά και πάλι υπάρχει πρόβλημα . ΄Το αλουμίνιο έχει πυκνότητα γύρω στο 2,7 g/cm³ και ένα αντικείμενο όπως το Σ₂ αν είναι από αλουμίνιο θα έχει όγκο 2.200 cm³ 2,2 λίτρα , ακόμα και κύβο να το φανταστείς θα έχει πλευρά 47 εκατοστά περίπου . . . .Που να το βάλεις όλο αυτό πάνω σε ένα άλλο επίσης από αλουμίνιο με το 1/3 του όγκου . Και να περιγράφεται μια ταλάντωση υλικού σημείου με πλάτους 5 έως 20 εκατοστών. Δύσκολοι καιροί για μια γόνιμη συμβίωση των μοντέλων με τη μητέρα Πραγματικότητα.

Επίλογος

Τα θέματα ήταν δύσκολα στο σύνολό τους;

Το να εκτιμήσει ένας εκπαιδευτικός το πόσο δυσκόλεψαν ή δεν δυσκόλεψαν τους μαθητές δεν καθόλου απλό ζήτημα και συνήθως οι ποικίλες εκτιμήσεις «ειδικών» με εκείνο το τετριμμένο «τα θέματα φέτος ήταν βατά» κινούνται συνήθως στη σφαίρα του «να πούμε κάτι μια και το μικρόφωνο είναι μπροστά μας»

Το μόνο στοιχείο που διαθέτω είναι μια ομολογημένη ή ανομολόγητη αμηχανία των 30 περίπου καθηγητών φυσικής στο βαθμολογικό κέντρο, όταν είδαν για πρώτη φορά τα θέματα, οι περισσότεροι με μεγάλη πείρα σε διδασκαλία στο Λύκειο. Εκτιμώ – αν και έχω πέσει ορισμένες φορές έχω πέσει έξω στις εκτιμήσεις αυτού του είδους - ότι τα θέματα – στο σύνολό τους, τα τέσσερα δηλαδή θέματα, πρέπει να δημιούργησαν ιδιαίτερες δυσκολίες στους χιλιάδες εξεταζόμενους, ίσως από τις μεγαλύτερες τα τελευταία χρόνια.

Ανδρέας Ιωάννου Κασσέτας