Α΄ Λυκείου

ΘΕΜΑΤΑ

ΓΡΑΠΤΩΝ ΠΡΟΑΓΩΓΙΚΩΝ ΕΞΕΤΑΣΕΩΝ στη ΦΥΣΙΚΗ. Μάιος 2010

Με το γράμμα g παριστάνεται η επιτάχυνση της βαρύτητας και εφόσον το σχετικό φαινόμενο εκδηλώνεται στην επιφάνεια της Γης,

η τιμή της θα θεωρείται ίση με 10 m/s². Τα σώματα που αναφέρονται σε όλα τα ζητήματα θεωρούνται «υλικά σημεία».

Το πρώτο θέμα

Να μεταφέρετε στην κόλλα σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη μοναδική

σωστή πρόταση. Δεν χρειάζεται να δικαιολογήσετε την επιλογή σας.

1. Ένα αντικείμενο μάζας 0,2 kg εκτοξεύεται κατακόρυφα προς τα άνω με ταχύτητα 10m/s.

a. Κατά τη στιγμή της εκτόξευσης, η κινητική του ενέργεια είναι ίση με 20 J

β. Κατά την κατακόρυφη κίνηση προς τα πάνω, σε μετατόπιση 3 μέτρων,

το έργο της δύναμης «βάρος» είναι αρνητικό και ίσο με – 6J

γ. Κατά την κατακόρυφη κίνηση προς τα πάνω, η δυναμική του ενέργεια συνεχώς ελαττώνεται

δ. Κατά τη στιγμή της εκτόξευσης, η ορμή του είναι ίση με 20 kgm/s ( 5 μονάδες )

2 Σε ένα αρχικώς ακίνητο σώμα μάζας 2 kg, το οποίο βρίσκεται εκτός πεδίου βαρύτητας,

ασκούνται δύο μόνο δυνάμεις κάθετες μεταξύ τους . Η μία (F₁) έχει μέτρο 8 Ν και η άλλη (F₂) 6 Ν.

α. η συνισταμένη των δύο δυνάμεων είνα 14 Ν

β. η επιτάχυνση του σώματος είναι μηδέν .

γ. η η συνισταμένη των δύο δυνάμεων είνα 10 Ν

δ. η επιτάχυνση του σώματος είναι 1m/s² . ( 5 μονάδες )

3. Ένας τεχνητός δορυφόρος μάζας m περιφέρεται γύρω από τη Γη με ταχύτητα μέτρου υ. Αν είναι Μ η μάζα του πλανήτη Γη, και η κίνηση θεωρηθεί ομαλή κυκλική με ακτίνα τροχιάς R

α. Η δύναμη που ασκεί ο πλανήτης Γη στον δορυφόρο είναι μεγαλύτερη από τη δύναμη που ασκεί ο δορυφόρος στον πλανήτη Γη.

β. H δύναμη που ασκεί ο πλανήτης Γη στον δορυφόρο είναι ίση με GMm/R²,

όπου G η σταθερά της παγκόσμιας έλξης

γ. Η επιτάχυνση του δορυφόρου είναι ίση με υ/R² .

δ. Η περίοδος της περιφοράς είναι ίση με 2πυ/R. ( 5 μονάδες )

4. Ένα βαρίδι κι ένα κεράσι αφήνονται ταυτόχρονα και απο το ίδιο ύψος μέσα σε σωλήνα κενού.

Το βαρίδι είναι βαρύτερο από το κεράσι

α. Η ορμή του κερασιού, κατά την πτώση διατηρείται σταθερή

β. Το βαρίδι φθάνει πρώτο στη βάση του σωληνα

γ. Η κινητική ενέργεια που έχει το κεράσι πριν φθάσει στη βάση του σωλήνα

είναι ίση με την κινητική ενέργεια που έχει το βαρίδι την ίδια εκείνη στιγμή

δ. Κατά τη διάρκεια της πτώσης, πριν αγγίξουν τη βάση τη σωλήνα, το άθροισμα κινητικής και δυναμικής ενέργειας διατηρείται σταθερό τόσο για το ένα αντικείμενο όσο και για το άλλο ( 5 μονάδες )

5. Να μεταφέρετε στην κόλλα σας το σύμβολο ( 5α, 5β, 5γ, 5δ, 5ε. ) που αντιστοιχεί σε καθένα από τα θέματα και δίπλα να σημειώσετε το γράμμα Σ ( εφόσον το θεωρείτε σωστό ) ή το γράμμα Λ ( εφόσον το θεωρείτε λάθος) . Δεν χρειάζεται να το δικαιολογήσετε .

5α . Κατά την κατακόρυφη κίνηση προς τα πάνω η δυναμική ενέργεια ( βαρύτητας ) του κινουμένου σώματος συνεχώς ελαττώνεται.

5β. Καθώς ο αλεξιπτωτιστής πέφτει με σταθερή ταχύτητα η αντίσταση του αέρα είναι μικρότερη από το βάρος του

5γ . Αν ένα σώμα σε σε ομαλή κυκλική κίνηση έχει συχνότητα 5 Hz , η περίοδός του θα είναι 5 s.

5δ. Κατά την κρούση δύο σωμάτων – κατά την οποία δεν ασκούνται εξωτερικές δυνάμεις - η ορμή του ενός σώματος μεταβάλλεται, η ορμή του άλλου σώματος μεταβάλλεται αλλά η ορμή του συστήματος διατηρείται σταθερή

5ε. Καθώς σπρώχνει κάποιος ένα αρχικά ακίνητο αυτοκίνητο και τελικά το μετακινεί , η δύναμη που ασκεί ο άνθρωπος στο αυτοκίνητο είναι μεγαλύτερη από τη δύναμη που ασκεί το αυτοκίνητο στον άνθρωπο. ( 5 μονάδες )

Το δεύτερο θέμα

1. Ένα αντικείμενο Σ, μάζας 0,4 kg, αφήνεται από ύψος 30 μέτρων από το έδαφος. Η αντίσταση του αέρα θεωρείται αμελητέα.

Να αντιγράψετε τον παρακάτω πίνακα στο τετράδιό σας και να τον συμπληρώσετε .

Ύψος του Σ από το έδαφος	Δυναμική ενέργεια του Σ	Κινητική ενέργεια του Σ
30 m
25m
15 m
5 m

Οι τιμές της δυναμικής ενέργειας βαρύτητας να θεωρηθούν ως προς το έδαφος. ( 8 μονάδες )

2. Πάνω σε μια λεία οριζόντια επιφάνεια δύο μικρές όμοιες μπίλιες – Σ₁ και Σ₂, – κινούνται η μία προς την άλλη με ταχύτητες ίσων μέτρων και συγκρούονται.

Μια μαθήτρια ισχυρίζεται ότι

« η ορμή του συστήματος ( των Σ₁ και Σ₂ ) μετά την κρούση θα είναι ίση με μηδέν».

ενώ ένας μαθητής υποστηρίζει ότι

« η κινητική ενέργεια του συστήματος πριν από την κρούση είναι ίση με μηδέν»

Με ποιον συμφωνείτε ; Με τη μαθήτρια, με τον μαθητή και με τους δύο ή με κανέναν από αυτούς ;

Να δικαιολογήσετε την απάντηση ( 4 μονάδες )

3. Ένα αρχικώς ακίνητο αντικείμενο Σ μάζας 0,5 kg βρίσκεται σε οριζόντια επιφάνεια και σε κάποια χρονική στιγμή ασκείται σε αυτό οριζόντια δύναμη μέτρου 5 Ν. Αν ο συντελεστής τριβής ολίσθησης είναι ίσος με 0,4 σας ζητούμε

α. Να κάνετε ένα σχήμα και να σχεδιάσετε τις ασκούμενες στο σώμα δυνάμεις. ( 3 μονάδες )

β. Να υπολογίσετε την τιμή της τριβής ολίσθησης ( 3 μονάδες )

γ. Να προσδιορίσετε την επιτάχυνση του αντικειμένου. ( 3 μονάδες )

δ. Να υπολογίσετε το έργο καθεμιάς από τις ασκούμενες στο Σ δυνάμεις σε μετατόπιση του Σ κατά 2 μέτρα ( 4 μονάδες )

Το τρίτο θέμα

1. Το σώμα Σ στο σχήμα είναι αρχικά ακίνητο στη θέση Α. Σε κάποια χρονική στιγμή ασκείται στο Σ οριζόντια δύναμη F η οποία διατηρείται σταθερή και το Σ κινείται στο λείο οριζόντιο επίπεδο. Σε κάποια χρονική στιγμή βρίσκεται στη θέση Β και αργότερα στη θέση Γ.

Με δεδομένο ότι ΑΒ = ΒΓ σας ζητούμε να κρίνετε ποιες από τις παρακάτω προτάσεις είναι σωστές, ποιες είναι λάθος και να δικαιολογήσετε κάθε απάντηση.

α. Η ενέργεια που μεταβιβάζεται ( μεταφέρεται) στο σώμα κατά την κίνηση από το Α στο Γ είναι διπλάσια από την ενέργεια που μεταβιβάζεται στο ίδιο σώμα κατά την κίνηση από το Α στο Β.

β. Το έργο της δύναμης «βάρος του Σ» κατά την κίνηση από το Α στο Γ είναι διπλάσιο από το έργο της δύναμης «βάρος του Σ» κατά την κίνηση από το Α στο Β.

γ. Η κινητική ενέργεια του Σ στο Γ είναι διπλάσια από την κινητική ενέργεια που είχε στη θέση Β. ( 9 μονάδες )

2. Ένα κιβώτιο 6 kg βρίσκεται σε ασανσέρ. Να προσδιορίσετε τη δύναμη την οποία ασκεί το πάτωμα του ασανσέρ στο κιβώτιο εάν το ασανσέρ α. ανεβαίνει με σταθερή ταχύτητα . β. ανεβαίνει με σταθερή επιτάχυνση 3 m/s². γ. κατεβαίνει με σταθερή επιτάχυνση 2 m/s² . ( 9 μονάδες )

3. Σε ένα από τα ηλιακά συστήματα του Γαλαξία μας, ένας πλανήτης περιφέρεται γύρω από το κεντρικό άστρο σε κυκλική τροχιά ακτίνας 4.10¹² m . Σε χρόνο 10⁷ s ολοκληρώνει μια πλήρη περιφορά .

α. Να κάνετε ένα σχήμα και να σχεδιάσετε το διάνυσμα της ταχύτητας του πλανήτη σε μια τυχαία στιγμή της περιφοράς και το διάνυσμα της επιτάχυνσης την ίδια στιγμή. Ο πλανήτης να θεωρηθεί υλικό σημείο.

β. Να υπολογίσετε το μέτρο της ταχύτητας και το μέτρο της επιτάχυνσης του πλανήτη ( 8 μονάδες )

Το τέταρτο θέμα

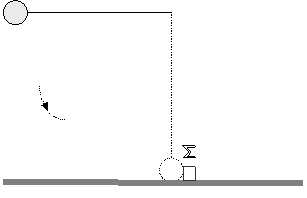Το σφαιρίδιο Α, δεμένο στο άκρο του τεντωμένου νήματος

έχει μάζα 0,4 kg και το αφήνουμε ελεύθερο από

τη θέση στην οποία το νήμα ( μήκους 0,45 m )

είναι τεντωμένο και οριζόντιο. Το σφαιρίδιο κινείται στο

άκρο του τεντωμένου νήματος και όταν το νήμα γίνεται

κατακόρυφο το σφαιρίδιο προσκρούει σε , αρχικά ακίνητο,

αντικείμενο Σ, μάζας 0,2 kg το οποίο βρίσκεται στο

έδαφος . Διαπιστώνεται ότι αμέσως μετά την κρούση

η ταχύτητα του Σ είναι 2 m/s και ενώ το Σ μετακινείται

στο οριζοντιο έδαφος με συντελεστή τριβής μ = 0,2,

το σφαιρίδιο Α συνεχίζει να αιωρείται στο άκρο του νήματος.

Σας ζητούμε, βασιζόμενοι σε φυσικούς νόμους, να υπολογίσετε α. Την ως προς το έδαφος δυναμική ενεργεια κάθε σώματος τη στιγμή που αφήνουμε ελεύθερο το σφαιρίδιο Α και το Σ είναι ακίνητο ( 4 μονάδες )

β. την ταχύτητα του σφαιριδίου τη στιγμή – πριν από την κρούση – που το νήμα γίνεται κατακόρυφο. ( 7 μονάδες )

γ. την απόσταση x , πάνω στο οριζόντιο έδαφος, την οποία θα διανύσει το Σ μέχρι να σταματήσει ( 8 μονάδες )

δ. την ταχύτητα του σφαιριδίου αμέσως μετά την κρούση ( 6 μονάδες)

Να θεωρήσετε ότι η μάζα του νήματος είναι αμελητέα και ότι η αιώρηση του εκκρεμούς γίνεται χωρίς ενεργειακές απώλειες.

Α΄ Λυκείου

12 θέματα

1. Κατά την ομαλή κυκλική κίνηση ενός υλικού σημείου, εκτός πεδίου βαρύτητας, σε τροχιά ακτίνας 50 m, ασκούνται δύο μόνο δυνάμεις η F₁ και η F₂. Αν η F₁ είναι 300 Ν και έχει κατεύθυνση προς το κέντρο του κύκλου να προσδιορίσετε τη δύναμη F₂, με δεδομένο ότι η μάζα του υλικού σημείου είναι 4 kg και η ταχύτητά του 50 m/s.

2. Ένα αντικείμενο μάζας 1 kg αφήνεται από την κορυφή κεκλιμένου επιπέδου γωνίας 30⁰ και ολισθαίνει κινούμενο προς τη βάση του κεκλιμένου επιπέδου . Αν ο συντελεστής τριβής ολίσθησησης είναι μ.

α. Ποιες δυνάμεις ασκούνται στο αντικείμενο ;

β. Να κάνετε ένα κατάλληλο σχήμα και να σημειώσετε τις δυνάμεις που ασκούνται στο αντικείμενο Α, σε μια τυχαία στιγμή της καθόδου.

γ. Να προσδιορίσετε ποιες από τις δυνάμεις αυτές εκτελούν έργο θετικό και ποιες αρνητικό

3. Διαθέτουμε μία σανίδα, ένα μοιρογνωμόνιο και ένα αντικείμενο .

Πώς μπορούμε να μετρήσουμε τον συντελεστή στατικής τριβής μεταξύ των δύο αντιστοίχων επιφανειών;

4, Ένα τραπέζι κι ένα βαρίδι ακίνητο πάνω του. Διαθέτουμε χρονόμετρο, δυναμόμετρο, θερμόμετρο και μετροταινία . Ποια απο αυτά τα όργανα πρέπει να επιλέξουμε ώστε να μετρήσουμε τη βαρυτική δυναμική ενέργεια του βαριδιού ως προς το έδαφος; Πώς θα γίνει η μέτρηση ;

5. Ένα αντικείμενο μάζας m αφήνεται από την κορυφή κεκλιμένου επιπέδου γωνίας θ και ολισθαίνει κινούμενο προς τη βάση του κεκλιμένου επιπέδου. Αν ο συντελεστής τριβής ολίσθησης είναι μ :

α. Να δώσετε απάντηση στο ερώτημα «Ποιες δυνάμεις ασκούνται στο αντικείμενο ;»

β. Να κάνετε ένα κατάλληλο σχήμα και να σημειώσετε τις δυνάμεις που ασκούνται στο αντικείμενο, σε μια τυχαία στιγμή της καθόδου.

γ. Να προσδιορίσετε ποιες από τις δυνάμεις αυτές εκτελούν έργο θετικό και ποιες αρνητικό

6. Να προσδιορίσετε α. την επιτάχυνση καθενός από τα δύο σώματα

β. τη δύναμη που ασκεί το ένα στο άλλο.

Η ασκούμενη οριζόντια δύναμη είναι 6 Ν.

Η μάζα του μεγαλύτερου σώματος είναι 1,2 kg

και η μάζα του άλλου 0,8 kg. Η τριβή να θεωρηθεί αμελητέα

7. Ένα βαρύ φλιτζάνι πάνω στο τραπέζι. Έχουμε διαπιστώσει προηγουμένως ότι το φλιτζάνι ζυγίζει 5 Ν .

και συμβαίνει να ξέρουμε ότι ο συντελεστής στατικής είναι 0,4.

Να προβλέψετε τι θα συμβεί στο φλιτζάνι ( θα μετακινηθεί ή θα μείνει ακίνητο )

εάν του ασκήσουμε χαμηλά α. οριζόντια δύναμη 1 Ν β. οριζόντια δύναμη 1,6 Ν

γ. δύναμη 4 Ν με κατεύθυνση λοξά προς τα κάτω,

έτσι ώστε να σχηματίζει γωνία 30⁰ με την επιφάνεια του τραπεζιού

8. Τα δύο αντικείμενα Σ₁ και Σ₂ έχουν ίσες μάζες, 500 g το καθένα, και βρίσκονται πάνω σε τραπέζι με συντελεστή τριβής 0, 2 και για τα δύο και συνδέονται με οριζόντιο νήμα αμελητέας μάζας. Ένα οριζόντιο ελατήριο αμελητέας μάζας έχει προσδεθεί στο Σ₁

και του ασκεί δύναμη

α. Να σημειώστε τις «εξωτερικές» δυνάμεις που ασκούνται στο σύστημα « Σ₁ , νήμα, Σ₂ ».

β. Να υπολογίσετε την επιτάχυνση του συστήματος.

γ. Να σημειώστε τις δυνάμεις που ασκούνται στο Σ₂ .

δ. Να υπολογίσετε τη δύναμη που ασκεί το τεντωμένο νήμα στο Σ₂ .

9. Η μάζα της Γης είναι 6. 10²⁴ kg. Πώς μέτρησαν οι άνθρωποι τη μάζα του πλανήτη ;

10. Από τις παρακάτω λέξεις και εξισώσεις να διαλέξετε τις κατάλληλες για να γεμίσουν τα κενά του κειμένου:

ΤΟ ΜΕΤΡΟ ΚΕΝΤΡΟΜΟΛΟΣ ΠΕΡΙΟΔΙΚΗ ΤΑΧΥΤΗΤΑ ΠΕΡΙΟΔΟΣ υ = 2πR/T

ΕΠΙΤΑΧΥΝΣΗ Η ΚΑΤΕΥΘΥΝΣΗ u² =a_κR ΣΥΧΝΟΤΗΤΑ ΔΙΑΤΗΡΕΙΤΑΙ ΜΕΤΑΒΑΛΛΕΤΑΙ υ = πR²/T

Κατά την ομαλή κυκλική κίνηση ενός υλικού σημείου η ταχύτητά του . . . . .. . . Αλλάζει συνεχώς . . . . . . . . . της, ενώ . . . . . . της διατηρείται σταθερό. Υπάρχει . . . . . . . η οποία χαρακτηρίζεται . . . . . . . καθώς το σχετικό διάνυσμα κατευθύνεται προς το κέντρο της τροχιάς. Η κίνηση είναι . . . . . καθώς το κινούμενο αντικείμενο ανά ίσα χρονικά διαστήματα ξαναβρίσκεται στη θέση του ανακτώντας την . . . . . .. . . του και την επιτάχυνσή του. Η . . . . . . . . . . . . σε αυτή την περίπτωση ορίζεται ως χρόνος απαιτούμενος για να διαγραφεί μία περιφέρεια. . Εύκολα αποδεικνύεται ότι η σχέση της ταχύτητας(υ) με την περίοδο (Τ) και την ακτίνα της τροχιάς (R ) είναι η . . . . . . . . . . ενώ -πολύ πιο δύσκολα- αποδεικνύεται ότι η σχέση της ταχύτητας με την κεντρομόλο επιτάχυνση (a_κ) και με την ακτίνα της τροχιάς είναι η . . . . . . . . . .

11. Δύο μπίλιες, η μία (Μ₁ ) μάζας 80 g και η άλλη (Μ₂) μάζας 50 gκινούνται η μία προς την άλλη με αντίθετες κατευθύνσεις και με ταχύτητες οι οποίες έχουν μέτρα 4m/s και 2m/s αντίστοιχα.

α .Να προσδιορισετε την κινητική ενέργεια του συστήματος και την ορμή του συστήματος των δύο σωμάτων πριν από την κρούση β. Μετά τη σύγκρουση η Μ₁ συνεχίζει να κινείται προς την κατεύθυνση που είχε πριν από τη σύγκρουση με ταχύτητα μέτρου 1,5m/s. Να προσδιορίσετε την ταχύτητα της Μ₂.

12. Πάνω σε οριζόντιο διάδρομο ένα αντικείμενο Μ₁ κινούμενο με σταθερή ταχύτητα πλησιάζει προς ένα άλλο ακίνητο αντικείμενο Μ₂ με το οποίο συγκρούεται και συσσωματώνεται. Δύο δευτερόλεπτα πριν από τη σύγκρουση τα δύο αντικείμενα απείχαν κατά

8 μέτρα. Σας ζητούμε να προβλέψετε πόσο θα απέχουν από το σημείο της συνάντησής τους δύο δευτερόλεπτα

μετά την σύγκρουση. Η μάζα του Μ₁ είναι 1000 g ενώ η μάζα του Μ₂ είναι 600 g. H χρονική διάρκεια της σύγκρουσης να θεωρηθεί αμελητέα.