Ανδρέας Ιωάννου Κασσέτας

Η Φυσική στην Α΄ Λυκείου .

Η ΔΙΔΑΣΚΑΛΙΑ 4

Σύμφωνα με τη Φυσική κάθε κίνηση που δεν είναι ευθύγραμμη είναι ΜΕΤΑΒΑΛΛΟΜΕΝΗ.

Αν ένα σημειακό αντικείμενο κινείται σε κυκλική τροχιά χωρίς να αυξομειώνεται η ταχύτητά του

η κίνησή του θεωρείται μεταβαλλόμενη διότι ΑΛΛΑΖΕΙ ΚΑΤΕΥΘΥΝΣΗ .

Αφού όμως δεν αυξομειώνεται
η ταχύτητά του
σημαίνει ότι είναι ΣΤΑΘΕΡΗ.

Οι φυσικοί δέχτηκαν ότι

η ταχύτητα

εκτός από μια τιμή

έχει και μια ΚΑΤΕΥΘΥΝΣΗ .

Και εφόσον η κατεύθυνση αλλάζει

θεωρούν ότι η ταχύτητα μεταβάλλεται

Μου είναι ιδιαίτερα δύσκολο να παραδεχτώ ότι μια ταχύτητα

που είναι συνεχώς

8m/s, 8m/s, 8m/s, 8m/s, 8m/s, 8m/s,

είναι «ταχύτητα που αλλάζει »

Αλλάζει εφόσον αλλάζει η κατεύθυνσή της κι ας είναι

η τιμή της συνεχώς 8 m/s.

Για τη φυσική, η ταχύτητα ενός σώματος

δεν απαντά μόνο στο «πόσο γρήγορα κινείται;» ,

αλλά και στο

«προς τα πού κινείται; » το σώμα .

Η ταχύτητα των φυσικών είναι μια παράξενη «ταχύτητα με κατεύθυνση».

Την παριστάνουν μάλιστα με ένα βελάκι που το λένε διάνυσμα.

Με αυτό περιγράφεται

σε κάθε στιγμή

και η κατεύθυνση της κίνησης

η οποία θεωρείται

κατεύθυνση της ταχύτητας. Η ταχύτητα στη Φυσική είναι μέγεθος διανυσματικό.

Και γιατί τη δημιούργησαν μέγεθος διανυσματικό

και δεν την άφησαν

όπως την καταλαβαίνουμε εύκολα

να απαντά δηλαδή

μόνο στο «πόσο γρήγορα», να είναι κυριολεκτικά μια ΤΑΧΥΤΗΤΑ ;

Για πολλούς λόγους. Ένας από αυτούς είναι η ΕΜΠΕΙΡΙΑ ότι

«για να στρίψει ένα κινούμενο σώμα»

ακόμα και χωρίς να αυξομειωθεί η ταχύτητά του

χρειάζεται προσπάθεια,

χρειάζεται να συμβεί κάποια επίδραση,

αργότερα αυτό θα το λέμε χρειάζεται να ασκηθεί ΔΥΝΑΜΗ

Εξάλλου και για να αυξομειωθεί η ταχύτητα ακόμα και σε ευθύγραμμη κίνηση

χρειάζεται επίσης κάποια επίδραση

Η ταχύτητα της Φυσικής, αυτή η παράξενη «ταχύτητα με κατεύθυνση»

επινοήθηκε έτσι ώστε να αλλάζει κάθε φορά που ασκείται δύναμη

και εφόσον δεν ασκείται δύναμη να διατηρείται σταθερή

Στην ευθύγραμμη ομαλή όπου η ταχύτητα ούτε αυξομειώνεται

ούτε αλλάζει κατεύθυνση

δεν χρειάζεται κάποια επίδραση;

Πώς συνεχίζει να κινείται το σώμα ;

Χωρίς κάποιος να το σπρώχνει ;

Οι φυσικοί λένε ότι

το σώμα συνεχίζει

να κινείται μόνο του

και το έχουν αποδείξει

Εντυπωσιάζομαι με όλα αυτά και νιώθω την ανάγκη να πω τι έχω καταλάβει.

Η ΕΥΘΥΓΡΑΜΜΗ ΟΜΑΛΗ ΚΙΝΗΣΗ είναι κάτι ξεχωριστό.

Είναι η μόνη κίνηση που μπορεί να συνεχίζεται χωρίς καμία παρέμβαση

Είναι η μόνη κίνηση με ταχύτητα σταθερή τόσο σε τιμή όσο και σε κατεύθυνση

Οποιαδήποτε άλλη κίνηση υλικού σημείου χρειάζεται παρέμβαση.

Σε οποιαδήποτε κίνηση που δεν είναι ευθύγραμμη ομαλή η ταχύτητα μεταβάλλεται.

Είναι κίνηση μεταβαλλόμενη.

Και στην ΕΥΘΥΓΡΑΜΜΗ κίνηση

κατά την οποία δεν αλλάζει η κατεύθυνσή της

η ταχύτητα είναι μέγεθος διανυσματικό ;

Για τους φυσικούς η ταχύτητα,

σε οποιαδήποτε κίνηση,

είναι μέγεθος διανυσματικό.

Ναι αλλά εμείς περιγράψαμε την ευθύγραμμη κίνηση

-τόσο την ομαλή όσο και την ομαλά επιταχυνόμενη –

χωρίς να χρειαστούμε την ταχύτητα-διάνυσμα ούτε και την επιτάχυνση-διάνυσμα

Η περιγραφή μιας ευθύγραμμης κίνησης

δεν χρειάζεται τα διανύσματα.

Αλλά σε πιο σύνθετα φαινόμενα

τα διανύσματα είναι αναγκαία

Ένα παράδειγμα ;

Ένα βαρκάκι διασχίζει το ποτάμι κάθετα στην όχθη.

Αν υποθέσουμε ότι δεν υπήρχε ρεύμα η ταχύτητά του υ_β θα είχε μία κατεύθυνση και μία τιμή.

Πώς είναι η ταχύτητα όταν υπάρχει ρεύμα.

Για να δώσουμε μια απάντηση πρέπει να χρησιμοποιήσουμε την ταχύτητα – διάνυσμα.

Και να προσθέσουμε τη διανυσματική ταχύτητα υ_β με τη διανυσματική ταχύτητα του ρεύματος

Εξάλλου το σημαντικό στα διανυσματικά είναι ο τρόπος με τον οποίο γίνεται η πρόσθεσή τους

Θα το συζητήσουμε αργότερα.

Και η ΘΕΣΗ είναι μέγεθος διανυσματικό.

Για τη Φυσική

η ΘΕΣΗ, η ΤΑΧΥΤΗΤΑ, η ΕΠΙΤΑΧΥΝΣΗ

ανήκουν στη μεγάλη οικογένεια των ΔΙΑΝΥΣΜΑΤΙΚΩΝ

Υποθέτω ότι υπάρχει

και άλλη οικογένεια μεγεθών τα οποία δεν είναι διανυσματικά.

Ακριβώς . Τα φυσικά μεγέθη

- οι έννοιες δηλαδή για τις οποίες επινοήσαμε τρόπους μέτρησης -

ανήκουν σε δύο οικογένειες .

Στη μία ανήκουν μεγέθη όπως η μάζα, η θερμοκρασία και η ενέργεια

τα οποία προσδιορίζονται ΜΟΝΟ με το με το μέτρο τους.

Είναι το λεγόμενα ΜΟΝΟΜΕΤΡΑ μεγέθη τα οποί α προστίθενται όπως οι αριθμοί.

Στην άλλη ανήκουν μεγέθη όπως η ταχύτητα και η δύναμη

για τον προσδιορισμό των οποίων απαιτείται εκτός το μέτρο και η ΚΑΤΕΥΘΥΝΣΗ.

Κάθε διανυσματικό παριστάνεται με ένα τόξο το οποίο δείχνει την κατεύθυνσή του και λέγεται ΔΙΑΝΥΣΜΑ.

Το ιδιαίτερο στοιχείο των διανυσματικών είναι ότι ΔΕΝ προστίθενται όπως οι θετικοί αριθμοί.

Μια δύναμη 8 μονάδων και μια δύναμη 6 μονάδων δεν κάνουν οπωσδήποτε μια δύναμη 14 μονάδων.

Για το «πώς προστίθενται» που είναι και το πιο ενδιαφέρον ζήτημα,

και θα το συζητήσουμε όταν ασχοληθούμε με την έννοια ΔΥΝΑΜΗ.

Για τη Φυσική, λοιπόν,

η έννοια ΘΕΣΗ είναι μέγεθος ΔΙΑΝΥΣΜΑΤΙΚΟ

ΘΕΣΗ σε μια ορισμένη χρονική στιγμή μιας ευθύγραμμης της κίνησης θεωρείται το διάνυσμα ΟΣ

όπου Ο η αρχή των αξόνων και Σ το γεωμετρικό σημείο

στο οποίο βρίσκεται το κινούμενο σώμα τη στιγμή εκείνη

Σε μία ευθύγραμμη κατά την οποία έχουμε θεωρήσει άξονα x να συμπίπτει

με την τροχιά, η αλγεβρική τιμή της θέσης

είναι ίση με την απόσταση

από την αρχή των αξόνων, προσημασμένη με θετικό πρόσημο

εφόσον το διάνυσμα έχει κατεύθυνση προς το + του άξονα

και στην αντίθετη περίπτωση πρόσημο αρνητικό

συμπίπτει δηλαδή με την τετμημένη του γεωμετρικού σημείου Σ

η μεταβολή της θέσης λέγεται ΜΕΤΑΤΟΠΙΣΗ

η ΤΑΧΥΤΗΤΑ

περιγράφει το «πόσο γρήγορα» αλλάζει η θέση,

τον ΡΥΘΜΟ ΜΕΤΑΒΟΛΗΣ ΤΗΣ ΘΕΣΗΣ

Σε μια ευθύγραμμη κίνηση το διάνυσμα της ταχύτητας

έχει την κατεύθυνση της μεταβολής θέσης,

την κατεύθυνση δηλαδή της κίνησης

ευθύγραμμη ομαλή κίνηση

Για κάθε διάνυσμα «θέση» αναφέρθηκε και η αλγεβρική τιμή του

ως προς ορισμένο άξονα . Το ίδιο ισχύει και για την ταχύτητα ;

Υπάρχουν αλγεβρικές τιμές της ταχύτητας ;

Σε μια ευθύγραμμη κίνηση μπορούμε να χρησιμοποιούμε και

τις αλγεβρικές τιμές της ταχύτητας. Αυτές έχουν νόημα μόνο

ως προς ορισμένο άξονα τον οποίο έχουμε εμείς επιλέξει.

Η αλγεβρική τιμή της ταχύτητας είναι η απόλυτη τιμή της ταχύτητας με πρόσημο .

Θα είναι θετική εφόσον κατά τη στιγμή εκείνη η κατεύθυνσή της είναι προς το συν (+) του άξονα.

Στην αντίθετη περίπτωση θα είναι αρνητική

Αν η απόλυτη τιμή της υ₁ είναι 3 m/s , η αλγεβρική τιμή θα είναι + 3 m/s

Αν η απόλυτη τιμή της υ₂ είναι 5 m/s , η αλγεβρική τιμή θα είναι -5 m/s

Και σε τι μας εξυπηρετούν

όλα αυτά τα ΑΛΓΕΒΡΙΚΑ ;

Εφόσον το φαινόμενο είναι ευθύγραμμη κίνηση μπορούμε να μη χρησιμοποιούμε

τα διανύσματα και να περιγράφουμε

την κίνηση με ΑΛΓΕΒΡΙΚΕΣ ΤΙΜΕΣ

Εφόσον σε μια κίνηση η ταχύτητα αλλάζει

χρησιμοποιούμε την έννοια ΜΕΤΑΒΟΛΗ ΤΑΧΥΤΗΤΑΣ

την οποία συμβολίζουμε με Δυ

Για να υπολογίσουμε ΑΦΑΙΡΟΥΜΕ

από την «τελική» ταχύτητα την αρχική Δυ = υ_τελ – υ_αρχ

η έννοια ΕΠΙΤΑΧΥΝΣΗ

περιγράφει

το «πόσο γρήγορα» αλλάζει η ταχύτητα,

τον ΡΥΘΜΟ ΜΕΤΑΒΟΛΗΣ ΤΗΣ ΤΑΧΥΤΗΤΑΣ.

Αν ο ρυθμός μεταβολής της ταχύτητας είναι σταθερός,

όπως στο φαινόμενο

«ευθύγραμμη ομαλά επιταχυνόμενη κίνηση»

η επιτάχυνση ορίζεται από τη σχέση

Για τη Φυσική

η έννοια ΕΠΊΤΑΧΥΝΣΗ

είναι μέγεθος ΔΙΑΝΥΣΜΑΤΙΚΟ

σε μια ευθύγραμμη κίνηση με αυξανόμενη ταχύτητα

το διάνυσμα της επιτάχυνσης έχει την κατεύθυνση της ταχύτητας

σε μια ευθύγραμμη κίνηση με μειωνόμενη ταχύτητα

το διάνυσμα της επιτάχυνσης έχει κατεύθυνση αντίθετη από εκείνη της ταχύτητας

Oι εξισώσεις x = ½αt² και υ = αt μας δίνουν τη θέση

και την ταχύτητα υπό την προϋπόθεση ότι

ΚΑΤΑ ΤΗΝ ΑΡΧΗ ΤΩΝ ΧΡΟΝΩΝ το κινούμενο αντικείμενο

βρισκόταν στην αρχή των αξόνων με μηδενική ταχύτητα

Τι θα ισχύει εάν ΚΑΤΑ ΤΗΝ ΑΡΧΗ ΤΩΝ ΧΡΟΝΩΝ

το κινούμενο αντικείμενο βρισκόταν στην αρχή των αξόνων

με ταχύτητα υ₀ ;

Η μετά χρόνο t θέση του x μπορεί να προσδιοριστεί

εάν το φανταστούμε επί χρόνο t να κινείται με σταθερή ταχύτητα υ₀

οπότε θα έχει μετατοπιστεί κατά υ_οt

και στη συνέχεια το φανταζόμαστε να κινείται επίσης επί χρόνο t

προς την κατεύθυνση της επιτάχυνσης με σταθερή επιτάχυνση

οπότε θα μετατοπιστεί κατά ½αt² .

Αυτό σημαίνει ότι τη χρονική στιγμή t

θα απέχει από την αρχή των αξόνων κατά

Η μετά χρόνο t ταχύτητά του υ μπορεί να προσδιοριστεί

αρκεί να εφαρμόσουμε τον ορισμό

της επιτάχυνσης στις χρονικές στιγμές 0 και t

Θα είναι α = Δυ/Δt άρα α =( υ - υ₀)/t

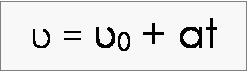
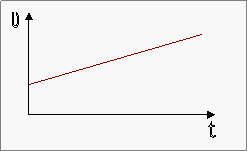
Κι αν η σταθερή επιτάχυνση

έχει αντίθετη κατεύθυνση

από την αρχική ταχύτητα ;

Εφόσον θεωρήσουμε τον άξονα έτσι ώστε κατά την αρχή των χρόνων να βρίσκεται στην αρχή των αξόνων

Η μετά χρόνο t θέση του μπορεί να προσδιοριστεί

εάν το φανταστούμε επί χρόνο t να κινείται με σταθερή ταχύτητα υ₀

οπότε θα έχει μετατοπιστεί κατά υ_οt

και στη συνέχεια να κινείται επί χρόνο t προς την κατεύθυνση της επιτάχυνσης

με σταθερή επιτάχυνση οπότε θα μετατοπιστεί κατά ½αt² .

οπότε προκύπτει

Ενώ η συνεχώς μειούμενη ταχύτητα θα δίνεται από τη σχέση

η οποία απορρέει από τον ορισμό της επιτάχυνσης

Αν δηλαδή εκτοξεύσουμε μια πέτρα

προς τα πάνω με ορισμένη ταχύτητα υ₀

η ΘΕΣΗ της y μετά χρόνο t θα είναι

ενώ η ταχύτητά της θα είναι ίση με

υ = υ₀ – gt

όπου g = |a| = 10 m/s², περίπου

Εξαιρετικό . Κατάλαβες ότι τέτοιου είδους κίνηση «επιβραδυνόμενη» με σταθερή επιτάχυνση

και με ταχύτητα που ελαττώνεται

είναι αυτή που ακολουθεί κάθε φορά που εκτοξεύουμε

ένα αντικείμενο κατακόρυφα προς τα πάνω.

Και η «επιβραδύνουσα» αυτή επιτάχυνση είναι η επιτάχυνση της βαρύτητας

Γιατί τη λέτε «επιβραδύνουσα επιτάχυνση »

και οχι επιβράδυνση ;

Διότι στη Φυσική δεν υπάρχει έννοια με το όνομα επιβράδυνση.

Η ΕΠΙΤΑΧΥΝΣΗ – διάνυσμα είναι η μοναδική έννοια που περιγράφει τις αλλαγέςτης ταχύτητας.

Και δεν μοιάζει με την επιτάχυνση της καθημερινής γλώσσας η οποία «μόνο επιταχύνει» .

Η επιτάχυνση-διάνυσμα της Φυσικής είναι υπεύθυνη για οποιαδήποτε μεταβολή της ταχύτητας

Αν έχει την ΙΔΙΑ κατεύθυνση με την ταχύτητα ΘΑ συμβεί ΑΥΞΗΣΗ της ταχύτητας χωρίς αλλαγή στην κατεύθυνση

Αν έχει κατεύθυνση ΑΝΤΙΘΕΤΗ από εκείνη της ταχύτητας θα συμβεί ΕΛΑΤΤΩΣΗ της ταχύτητας χωρίς αλλαγή στην κατεύθυνση

Αν είναι ΚΑΘΕΤΗ στην ταχύτητα το σώμα θα στρίψει, θα συμβεί αλλαγή στην κατεύθυνση χωρίς αυξομείωση της ταχύτητας.

Αλλά για το θέμα αυτό θα συζητήσουμε αργότερα

Με τις εξισώσεις

y = υ₀t – ½gt² και υ = υ₀ – gt

μπορείς να προβλέψεις πόσο χρονικό διάστημα

θα ανεβαίνει ένα βότσαλο αν το εκτοξεύσεις κατακόρυφα με μια ταχύτητα ας πούμε 4 m/s.

Αν στη σχέση της ταχύτητας βάλουμε υ = 0

θα προκύψει 0 = υ_ο – gt_αν, όπου t_αν ο χρόνος της «ανόδου». t_αν = υ₀/g θα είναι 0,4 s.

Εγώ θα μπορούσα μα δώσω

σε ένα βότσαλο ταχύτητα 4 m/s ;

Αν βάλεις τον χρόνο ανόδου υ₀/g στην y = υ₀t – ½gt²

προκύπτει το μέγιστο ύψος σε μια βολή προς τα πάνω .

Είναι ίσο με υ₀²/2g.

Αυτό σημαίνει ότι δίνοντας σε ένα βότσαλο ταχύτητα 4 m/s, θα πάει 0,8 μέτρα ψηλά.

Αυτό σημαίνει ότι σε ένα βότσαλο μπορείς να δώσεις ταχύτητα ακόμα μεγαλύτερη.

Αν δηλαδή εκτοξεύσω ένα βαρύ αντικείμενο από ύψος ένα μέτρο με ταχύτητα 8 m/s προς το ταβάνι της αίθουσας

Αυτό θα φθάσει σε ύψος 3,2 μέτρων από το σημείο εκτόξευσης,

άρα θα φθάσει ακριβώς στο ταβάνι της αίθουσας τη στιγμή που θα μηδενίζεται η ταχύτητά του

Αυτό θα συμβεί σχεδόν όπως το λες γιατί υπολογίζω το ύψος της αίθουσας γύρω στα 4 μέτρα

και είπες ότι η εκτόξευση γίνεται από ένα μέτρο πάνω από το πάτωμα.

Δοκίμασε να το κάνεις και αν καταφέρεις να του δώσεις τόση κατακόρυφη ταχύτητα τόση

ώστε φθάσει ακριβώς στο ταβάνι της αίθουσας τη στιγμή που θα μηδενίζεται η ταχύτητά του

θα έχεις καταφέρει να δώσεις ταχύτητα γύρω στο 7,5 m/s.