Ανδρέας Ιωάννου Κασσέτας

Η πηγή της έμπνευσης είναι η ομιλία του καθηγητή Σταύρου Θεοδωράκη στο Παιδαγωγικό Ινστιτούτο Κύπρου.

Τα τρία πρώτα από τα προτεινόμενα για λύση συνιστούν παραλλαγές αντίστοιχων προβλημάτων

τα οποία παρουσίασε κατά την ομιλία του. Το τέταρτο είναι ακριβώς το δικό του πρόβλημα

1. Στην κορυφή του ημισφαιρικού λόφου ακτίνας R το σημειακό αντικείμενο Σ έχει οριζόντια ταχύτητα υ₀. Τι θα συμβεί εάν

α. υ₀= √(3gR/2)

β. υ₀= √(gR/2) ;

Το Σ θα διατηρείται σε επάφή με τον τον λόφο

μέχρι να φθάσει στο έδαφος ;

Η τριβή θεωρείται αμελητέα.

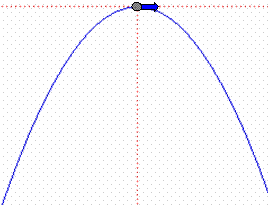
2. Στην κορυφή ενός λόφου η κατακόρυφη τομή του οποίου είναι παραβολική y = ρx² το σημειακό αντικείμενο Σ έχει οριζόντια ταχύτητα υ₀. Εάν υ₀= √(g/4ρ) τι θα συμβεί στη συνέχεια; Το Σ θα διατηρείται πάνω στον λόφο; Η τριβή θεωρείται αμελητέα.

.

3. Η φιάλη περιέχει αρχικά ομοιογενές μίγμα ίσων όγκων λαδιού και νερού και η πίεση στον πυθμένα είναι p. Με την παρόδο του χρόνου το λάδι θα βρεθεί στο επάνω μέρος . Κάποιος ισχυρίζεται πως όταν συμβεί αυτό, η πίεση p’ στον πυθμένα θα είναι ίση με την αρχική πίεση p, δεδομένου ότι το βάρος δεν άλλαξε.

Έχει δίκιο ;

4. Το κυκλικό σύρμα έχει μάζα m/2 και είναι κρεμασμένο

από κατακόρυφο σπάγκο αμελητέας μάζας .

Δύο όμοιες χάντρες - καθεμιά μάζας m –

αφήνονται ταυτόχρονα από την κορυφή – σημείο ανάρτησης –

του κυκλικού σύρματος

και ολισθαίνουν

με αμελητέα τριβή .

Τι θα συμβεί ;

Θα φθάσουν στη βάση σύρματος ; .

.