Ανδρέας Ιωάννου Κασσέτας

Θα περιοριστώ στις ΑΠΑΝΤΗΣΕΙΣ – ΛΥΣΕΙΣ των θεμάτων Φυσικής κατεύθυνσης 2010

Θα επανέλθω με σχόλια

ΘΕΜΑ Β

Β1. Στην ελεύθερη επιφάνεια ενός υγρού δύο σύγχρονες πηγές αρμονικών κυμάτων εκτελούν κατακόρυφες ταλαντώσεις με συχνότητα f και δημιουργούν εγκάρσια κύματα ίδιου πλάτους Α . Ένα σημείο Σ της επιφάνειας του υγρού ταλαντώνεται εξ αιτίας της συβολής των δύο κυμάτων με πλάτος 2Α . Αν οι δύο πηγές εκτελέσουν ταλάντωση με συχνότητα 2f και το ίδιο πλάτος Α, τότε το σημείο Σ θα α. ταλαντωθεί με πλάτος 2Α . β. ταλαντωθεί με πλάτος 4 Α γ. παραμένει ακίνητο

Να επιλέξετε τη σωστή απάντηση ( μονάδες 2 )

Να δικαιολογήσετε την επιλογή σας ( μονάδες 6 ) Μονάδες 8

Ας είναι r₁ και r₂ οι αποστάσεις του Σ από τις δύο πηγές

Αν είναι λ το μήκος κύματος, στην πρώτη περίπτωση που η συχνότητα είναι f και η ταχύτητα διάδοσης υ, ισχύει λ= υ/f . Εφόσον το πλάτος της ταλάντωσης του Σ είναι 2Α

ισχύει r₁ – r₂ = κ λ = κυ/f, όπου ο κ ΑΚΕΡΑΙΟΣ

Αν είναι λ’ το μήκος κύματος, στην περίπτωση που η συχνότητα είναι 2f και η ταχύτητα διάδοσης είναι βέβαια και πάλι υ, για το μήκος κύματος λ ισχύει λ΄= υ/2f .

Ας είναι, στη δεύτερη περίπτωση ρ ένας άγνωστος αριθμός για τον οποίο r₁ – r₂ = ρλ΄ r₁ – r₂ = ρυ/2f

Εφόσον η διαφορά r₁ – r₂ είναι ίδια ρυ/2f = κ υ/f, άρα ρ = 2κ και εφόσον ο κ είναι ακέραιος θα είναι ακέραιος και ο ρ. Το σημείο Σ, θα είναι σημείο η διαφορά των αποστάσεων του οποίου είναι ίση με ακέραιο πολλαπλάσιο του μήκους κύματος θα εκτελεί και πάλι ταλάντωση με πλάτος 2Α..

Β2. Δίσκος μάζας Μ είναι στερεωμένος στο πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k, και ισορροπεί

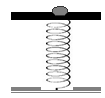( όπως στο σχήμα ) . Το άλλο άκρο του ελατηρίου είναι στερεωμένο στο έδαφος.

Στον δίσκο τοποθετούμε χωρίς αρχική ταχύτητα σώμα μάζας m.

Το σύστημα εκτελεί απλή αρμονική ταλάντωση. Η ενέργεια της ταλάντωσης είναι :

α. ½ m²g²/k β. ½ Μ²g²/k γ. ½ (m+Μ)2g² /k

Να επιλέξετε τη σωστή απάντηση ( μονάδες 2)

Να δικαιολογήσετε την επιλογή σας ( μονάδες 6) Μονάδες 8

Η λύση

Όταν ισορροπεί μόνος του ο δίσκος ισχύει Mg = kδ (1) , όπου δ , η απόλυτη διαφορά του μήκους του ελατηρίου από το φυσικό μήκος.

Όταν τοποθετήσουμε χωρίς αρχική ταχύτητα το σώμα μάζας m, η ταχύτητα εκείνη τη στιγμή του συστήματος στη θέση θ1 είναι μηδενική. Στη συνέχεια το σύστημα εκτελεί κατακόρυφη αρμονική ταλάντωση, με σταθερά ίση με k και με θέση ισορροπίας το σημείο στο οποίο οι ασκούμενες στο σύστημα δυνάμεις ισορροπούν.

Στη θέση εκείνη της ισορροπίας mg+Μg = k( δ+Α) (2)

Η απόσταση Α της θέσης εκείνης από το θέση θ₁ στην οποία η ταχύτητα του συστήματος είναι μηδενική, είναι το πλάτος της ταλάντωσης. Από τις (1) και (2) προκύπτει Α = mg/k , άρα η ενέργεια του ταλαντωτή θα είναι

½kA ² = ½m²g²/k

Β3. Δύο σώματα με μάζες m₁ = 2 kg και m₂ = 3 kg κινούνται χωρίς τριβές στο ίδιο οριζόντιο 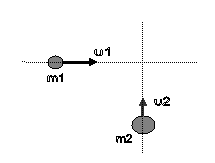επίπεδο και σε κάθετες διευθύνσεις με ταχύτητες υ ₁ = 4 m/s και υ₂ = 2 m/s ( όπως στο σχήμα ) και συγκρούονται πλαστικά.

Η κινητική ενέργεια του συσσωματώματος είναι :

α. 5 J β. 10 J γ. 20 J

Να επιλέξετε τη σωστή απάντηση ( μονάδες 2)

Να δικαιολογήσετε την επιλογή σας ( μονάδες 7) Μονάδες 9

Η λύση

Κατά τη εξέλιξη του φαινομένου διατηρείται η ορμή του συστήματος.

Πριν από την κρούση, για την ορμή του συστήματος – διανυσματικό άθροισμα των ορμών – εφόσον τα δυο διανύσματα είναι κάθετα μεταξύ τους, ισχύει

p_πριν² = ( m₁υ₁)² + (m₂υ₂)²

Η ορμή συνεπώς του συστήματος είναι ένα διάνυσμα με μέτρο p_πριν = 10kgm/s

Για την ορμή του ίδιου συστήματος μετά τη συσσωμάτωση

ισχύει p_μετά = ( m₁υ+ m₁₁)V

Εφόσον p_πριν= p_μετά

(m₁+ m₂)V = p_πριν V = p_πριν/(m₁+ m₂) V = 2 m/s

Το μέτρο συνεπώς της ταχύτητας του συσσωματώματος – και αυτό εν προκειμένω μας ενδιαφέρει διότι ζητούμενο είναι μόνο η τιμή της κινητικής ενέργειας - θα είναι 2 m/s

Άρα η κινητική ενέργεια θα είναι ίση με ½(m₁+ m₂) V² = 10 J.

Το θέμα Β , στο σύνολό του, είναι κατά την άποψή μου αξιοπρεπές

ΘΕΜΑ Γ

Στο κύκλωμα του σχήματος δίνονται : πηγή ηλεκτρεγερτικής δύναμης Ε = 5 V μηδενικής εσωτερικής αντίστασης, πυκνωτής χωρητικότητας C = 8. 10^-6 F ,πηνίο με συντελεστή 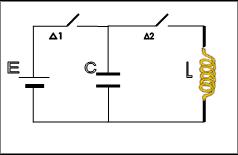αυτεπαγωγής L = 2.10^-2 H .

Αρχικά ο διακόπτης Δ₁ είναι κλειστός και ο διακόπτης Δ₂ ανοιχτός.

Γ1. Να υπολογίσετε το φορτίο του Q πυκνωτή Μονάδες 6

Ανοίγουμε τον διακόπτη Δ₁ και τη χρονική στιγμή t = 0 κλείνουμε τον διακόπτη Δ₂. Το κύκλωμα LC αρχίζει να εκτελεί αμείωτες ηλεκτρικές ταλαντώσεις .

Γ2. Να υπολογίσετε την περίοδο των ηλεκτρικών ταλαντώσεων Μονάδες 6

Γ3. Να γράψετε την εξίσωση σε συνάρτηση με τον χρόνο για την ένταση του ηλεκτρικού ρεύματος που διαρρέει το πηνίο. Μονάδες 6

Γ4. Να υπολογίσετε το ηλεκτρικό φορτίο του πυκνωτή τη χρονική στιγμή κατά την οποία η ενέργεια του μαγνητικού πεδίου είναι τριπλάσια απο την ενέργεια του ηλεκτρικού πεδίου στον πυκνωτή . Μονάδες 7

Η λύση

Γ1. Σύμφωνα με τον ορισμό της έννοιας «χωρητικότητα» για τον συγκεκριμένο πυκνωτή φορτισμένο με τάση V ισχύει C = Q/V άρα Q = CV. Άρα εφόσον η τάση είναι ίση με την ηλεκτρεγερτική δύναμη Q = 40.10^-6 C

Γ2. Για την περίοδο της ταλάντωσης ισχύει Τ = 2π √LC Τ = 8π. 10^-4 s

Γ3. i = - 0,1 ημ 2500t

Γ4. Εφόσον η ηλεκτρική ταλάντωση είναι αμείωτη, σύμφωνα με τη διατήρηση της ενέργειας

½Q²/C = U_B + U_E

τη χρονική στιγμή που U_B = 3U_E , ½ Q²/C = 4U_E

Για την ενέργεια την αποθηκευμένη στο ηλεκτρικό πεδίο του πυκνωτή τη στιγμή εκείνη ισχύει

U_E = ½q²/C, όπου q το ζητούμενο ηλεκτρικό φορτίο του πυκνωτή

½Q²/C = 4U_E ½Q²/C = 4. ½q²/C

|q| = Q/4 |q| = 20.10^-6 C

Το απόλυτο, επειδή το μεν σύμβολο Q παριστάνει θετική ποσότητα το δε q -

στιγμιαίο φορτίο του πυκνωτή – στις σχετικές εξίσώσεις παριστάνει αλγεβρική ποσότητα

Το θέμα Γ, στο σύνολό του, είναι κατά την άποψή μου αρκετά απλό «για θέμα Γ»

ΘΕΜΑ Δ.

Θέμα Δ

Θέλουμε να μετρήσουμε πειραματικά την άγνωστη ροπή αδράνειας δίσκου μάζας m = 2 kg και ακτίνας r = 1 m .

Για το σκοπό αυτό αφήνουμε τον δίσκο να κυλίσει χωρίς ολίσθηση σε κεκλιμένο επίπεδο γωνίας φ = 30⁰ ξεκνώντας από την ηρεμία. Διαπιστώνουμε ότι ο δίσκος διανύει την απόσταση x = 2 m σε χρόνο t = 1 s .

Δ1. Να υπολογίσετε τη ροπή αδράνειάς του ως προς τον άξονα που διέρχεται από το κέντρο μάζας του και είναι κάθετος στο επίπεδό του. Μονάδες 7

Δ2. Από την κορυφή του κεκλιμένου επιπέδου αφήνονται να κυλίσουν ταυτόχρονα δίσκος και δακτύλιος ίδιας μάζας Μ και ίδιας ακτίνας R. Η ροπή αδράνειας του δίσκου είναι Ι₁ = ½MR ² και του δακτυλίου Ι₂ = MR² ως προς τους άξονες που διέρχονται από τα κέντρα μάζας του και είναι κάθετοι στα επίπεδά τους. Να υπολογίσετε ποιο από τα σώματα κινείται με τη μεγαλύτερη επιτάχυνση. Μονάδες 4

Συνδέουμε με κατάλληλο τρόπο τα κέντρα μάζας των δύο στερεών, όπως φαίνεται και στο σχήμα, με ράβδο αμελητέας μάζας, η οποία δεν εμποδίζει την περιστροφή τους και δεν ασκεί τριβές. Το σύστημα κυλίεται στο κεκλιμένο επίπεδο χωρίς να ολισθαίνει

Δ3. Να υπολογίσετε τον λόγο των κινητικών ενεργειών Κ₁/Κ₂, όπου Κ₁ η κινητική ενέργεια του δίσκου και Κ₂ η κινητική ενέργεια του δακτυλίου. Μονάδες 6

Δ4. Αν η μάζα κάθε στερεού είναι Μ = 1,4 kg, να υπολογίσετε τις δυνάμεις που ασκεί η ράβδος σε κάθε σώμα.

Μεταφέρετε το σχήμα στο τετράδιό σας και σχεδιάστε τις πιο πάνω δυνάμεις.

Να μην χρησιμοποιήσετε το χαρτί μιλιμετρέ που βρίσκεται στο τέλος του τετραδίου

Δίνεται : g = 10 m/s² , ημ 30^ο = ½ Μονάδες 8

Θέλουμε να μετρήσουμε πειραματικά την άγνωστη ροπή αδράνειας

Πριν προχωρήσουμε στη λύση είναι αδύνατον να μην σταθούμε με σεβασμό μπροστά στη συγκεκριμένη ΕΠΙΛΟΓΗ.

Επιτέλους. Να ναι καλά αυτός που επέλεξε το θέμα με την ΠΕΙΡΑΜΑΤΙΚΗ ΜΕΤΡΗΣΗ ΤΗΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ.

Έβαλε δηλαδή για πρώτο ζήτημα , ΤΗΝ ΥΠΟΧΡΕΩΤΙΚΗ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ, την οποία δεν κάνουμε παρά ελάχιστοι , μολονότι είναι η ΜΟΝΗ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ για τη Φυσική κατεύθυνσης. Και με δεδομένο ότι τα θέματα αυτών των εξετάσεων ΕΠΙΔΡΟΥΝ περισσότερο από οτιδήποτε άλλο στη μορφή της διδασκαλίας οφείλουμε να παραδεχτούμε ότι ήταν μια ιδιαίτερα θετική επιλογή. Επιλογή η οποία για τους πιο αισιόδοξους από μας θα μπορούσε να ανοίξει ένα παράθυρο σε μια διδασκαλία που θυμίζει ότι η Φυσική δεν είναι μόνο

« κάποιοι τύποι » τους οποίους πρέπει να τους χειριζόμαστε κατάλληλα, αλλά Φυσική είναι και το ερώτημα «κύριε, κύριε . . πώς μετράμε στο εργαστήριο ττη ροπή αδράνειας ;» , Φυσική είναι και το ότι

πιάνουμε με τα χέρια μας τον κύλινδρο τον ζυγίζουμε, τον αφήνουμε να κυλίση στο κεκλιμένο, μετράμε με φωτοπύλες τον μικρό εκείνο χρονικό διαστημα, μετράμε με μετροταινία κάποια απόσταση, ξανακάνουμε το ίδιο αλλάζοντας τη γωνία και πάλι και πάλι, μέχρι να πετύχουμε τον στόχο

Η λύση

Δ1. Εστιάζουμε στην κίνηση του κέντρου μάζας . Η κίνηση αυτή ειναι ευθύγραμμη και επιδιώκουμε να ερευνήσουμε εάν η επιτάχυνση είναι χρονικά σταθερή

Η κύλιση του δίσκου αναλύεται σε μεταφορική με την ταχύτητα του κέντρου μάζας και σε στροφική περί άξονα που περνά από το κέντρο μάζας. Εφαρμόζουμε τον νόμο της κίνησης για τη στροφική κίνηση

Τr = I_cmα_γων (1) - όπου Τ η στατική τριβή – . Εφόσον η κύλιση εξελίσσεται χωρίς ολίσθηση, για την επιτάχυνση του κέντρου μάζας ισχύει a_cm =α_γωνr (1), οπότε Τ = I_cmα_cm /r² . (3)

Για την κίνηση του κέντρου μάζας, σύμφωνα με τον δεύτερο νόμο του Νεύτωνα, ισχύει

mgημφ – Τ = ma_cm (4)

Από τις εξισώσεις αυτές προκύπτει a_cm = mgημφ/(m + I_cm/r²) (5), σχέση που καταδεικνύει ότι η επιτάχυνση του κέντρου μάζας διατηρείται σταθερή.

Κατά συνέπεια ισχύει x = ½ a_cmt² , άρα a_cm=2x/ t² a_cm= 4 m/s² . (6).

Εφόσον η τιμή του a_cm είναι πλέον γνωστή, βλέπουμε τη σχέση (5) ως εξίσωση με άγνωστο το I_cm, και την λύνουμε ως προς I_cm. I_cm = mgr²ημφ/α_cm – mr². I_cm = 0,5 kgm².

Δ2.

Εφόσον η κίνηση κάθε σώματος είναι κύλιση χωρίς ολίσθηση , εφαρμόζουμε, όπως και προηγουμένως τον νόμο για τη στροφική κίνηση , ΤR = I_cmα_γων την συνδυάζουμε με την a_cm =α_γωνr και με την εφαρμογή του δεύτερου νόμου για την επιτάχυνση του κέντρου μάζας

mgημφ – Τ = ma_cm και καταλήγουμε στην a_cm = Mgημφ/(M + I_cm/R²)

Θέτουμε για τον δίσκο I_cm1 = ½MR ² . και για τον δακτύλιο I_cm2 = MR ² οπότε

a_cm1 = 2gημφ/3 a_cm2 = ½gημφ

Τελικά . ΤΟ ΚΕΝΤΡΟ ΜΑΖΑΣ ΤΟΥ ΔΙΣΚΟΥ ΚΙΝΕΙΤΑΙ ΜΕ ΜΕΓΑΛΥΤΕΡΗ ΕΠΙΤΑΧΥΝΣΗ από εκείνη του ΚΕΝΤΡΟΥ ΜΑΖΑΖ ΤΟΥ ΔΑΚΤΥΛΙΟΥ .

Ο λόγος των μέτρων των επιταχύνσεων είναι a_cm1 /a_cm2 = 4/3

Δ3. Το βασικό ζήτημα είναι ότι « τα δύο κέντρα μάζας, κατά την ευθύγραμμη κίνησή τους, έχουν, σε κάθε χρονική στιγμή, ίσες ταχύτητες- υ_cm η τιμή της κοινής ταχύτητας - και ίσες επιταχύνσεις ».

Το ίδιο ισχύει και για τις τιμές της γωνιακής ταχύτητας ω, της «συνιστώσας» στροφικής κίνησης, η οποία – εφόσον η κύλιση εκδηλώνεται χωρίς ολίσθηση - συνδέται με την υ_cm με τη σχέση υ_cm = ω R

Η κινητική ενέργεια του κυλιόμενου δίσκου θα είναι

Για τον δίσκο Κ₁ = ½Μυ_cm² +½ Ι₁ω² Κ₁ = ½Μυ_cm² + ½ ½MR²ω² Κ₁ = ¾ Μυ_cm² (7).

Για τον δακτύλιο Κ₂ = ½Μυ_cm² + ½Ι₂ ω² Κ₂ = ½Μυ_cm² + ½MR²ω² Κ₂ = Μυ_cm² (8).

Κ₁ /K₂ = ¾

Δ4. Ένα κεντρικό ζήτημα είναι το «ΑΜΕΛΗΤΕΟ» στην τιμή της μάζας της ράβδου.

Για τη μεταφορική κίνηση της ράβδου

Το σώμα ράβδος εκτελεί μεταφορική κίνηση με την κοινή επιτάχυνση των δύο κέντρων μάζας (δίσκου και δακτυλίου και εφόσον η μάζα του ΘΕΩΡΕΙΤΑΙ ΑΜΕΛΗΤΕΑ, ενώ η επιτάχυνσή του ΕΙΝΑΙ διάφορη του μηδενός, – η συνισταμένη των δυνάμεων πρέπει, βάση του δεύτερου νομου της κίνησης - να είναι ΑΜΕΛΗΤΕΑ και να θεωρηθεί ίση με μηδέν .

Οι δυνάμεις που ασκούνται στη ράβδο είναι δύο . Η δύναμη που της ασκεί ο δίσκος και η δύναμη που τις ασκεί ο δακτύλιος . Οι δύο αυτές δυνάμεις πρέπει συνεπώς να είναι αντίθετες. Με βάση τον τρίτο νόμο, αντίθετης κατεύθυνσης και ίσα μέτρα (έστω F) θα έχουν και η δύναμη F_ρδακτ που ασκεί η ράβδος στον δακτύλιο και η δύναμη F_ρδίσκο που ασκεί η ράβδος στον δίσκο .

Για την κύλιση του σώματος δακτύλιος .

Ποια είναι όμως η κατεύθυνση της δύναμης την οποία ασκεί η ράβδος στον διακτύλιο ;

Έχει, υποθέτω, σκόπιμα, προηγηθεί το ερώτημα για τη σχέση των δυο επιταχύνσεων και ο μαθητής έχει διαπιστώσει ότι ο δίσκος «κατηφορίζει» πιο γρήγορα. Αυτό του δημιουργεί , δικαιολογημένα, την ιδέα ότι ο δίσκος παρασύρει τον δακτύλιο , τον τραβάει προς τα κάτω.

Η ράβδος έλκει τον δακτύλιο, η ασκούμενη δηλαδή δύναμη F_ρδακτ έχει κατεύθυνση προς «τα κάτω»

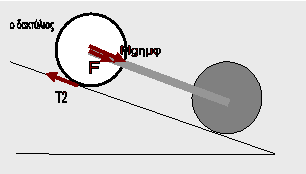Έστω το μέτρο της F

Σχετικά με την κίνηση του κέντρου μάζας F + Μgημφ – Τ₂ = Μa_cm

Για τη «συνιστώσα» στροφική κίνηση Τ₂R = I₂a_γων Τ₂R = ΜR²a_γων

και δεδομένου ότι a_cm = Ra_γων Τ₂ = Μa_cm

Από τις σχέσεις αυτές προκύπτει

F + mgημφ = 2ma_cm (9) .

Ένα επίσης «λεπτό» ζήτημα είναι η διαφορά στις τιμές της στατικής τριβής Τ₂ που ασκείται στον δακτύλιο και της στατικής τριβής Τ₁ που ασκείται στον δίσκο

Για την κύλιση του σώματος δίσκος

Η ασκούμενη στον δίσκο δύναμη F_ρδίσκο – εκ μέρους της ράβδου –

έχει αντίθετη κατεύθυνση από τη F_ρδακτ αλλά το μέτρο της θα είναι F .

Για την κίνηση του κέντρου μάζας Mgημφ – F – Τ₁ = Μa_cm

Για τη «συνιστώσα» στροφική κίνηση Τ₁R = I₁a_γων

Τ₁R = ½ΜR²a_γων Τ₁ = ½Μa_cm

Από τις σχέσεις αυτές προκύπτει

Μgημφ – F = 3/2 ma_cm (10) .

Από τις (9) και (10)

Μετά από διαίρεση κατά μέλη F = Μgημφ/7 F = 1 Ν

Προκύπτει επίσης a_cm= 20/7 m/s² Τ₁ = 2 N Τ₂= 4 N

Ανδρέας Ιωάννου Κασσέτας

Τετάρτη 26 Μαίου 2010, ώρα 18.00