Και είπεν ο κύριος :

Εκτοξευουμε μια πέτρα οριζόντια. Μπορούμε να προβλέψουμε «που θα βρίσκεται», σε κάθε χρονική στιγμή στο μέλλον;

1. Σύνθετη κίνηση . Αρχή της ανεξαρτησίας

Ένα από αυτά που μας άφησε ως κληρονομιά ο «δάσκαλός μας» ο Γαλιλαίος είναι η εξαιρετική ιδέα με βάση την οποία

μπορούμε να το ΠΡΟΒΛΕΠΟΥΜΕ. Με την ίδια θεωρία μπορούμε επίσης να προβλέπουμε και τη μορφή της τροχιάς.

Θεώρησε την κίνηση της πέτρας ως το αποτέλεσμα ΔΥΟ ανεξάρτητων κινήσεων οι οποίες γίνονται ταυτόχρονα

από την πέτρα . Οι δύο αυτές συνιστώσες της κίνησης ούτε μπλέκονται μεταξύ τους ούτε εμποδίζουν η μία την άλλη .

Οι δύο αυτές κινήσεις είναι

α. η οριζόντια κίνηση που θα έκανε το αντικείμενο αν δεν υπήρχε βαρύτητα

( ΕΥΘΥΓΡΑΜΜΗ ΟΜΑΛΗ ) και

β. η κατακόρυφη κίνηση που θα έκανε το αντικείμενο αν δεν είχε ταχύτητα και αφηνόταν ελεύθερο

( ΟΜΑΛΑ ΕΠΙΤΑΧΥΝΟΜΕΝΗ, με επιτάχυνση g )

για να εφαρμόσει στη συνέχεια τη λεγόμενη Αρχή της Ανεξαρτησίας των κινήσεων.

Η μετά χρόνο t ΘΕΣΗ θέση ενός κινητού που συμμετέχει σε δύο κινήσεις προσδιορίζεται, 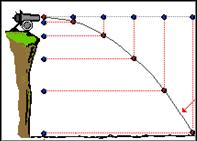εάν φανταστούμε το σώμα να εκτελεί επί χρόνο t πρώτα τη μία κίνηση - ανεξάρτητα από την άλλη - και αφού προσδιοριστεί το σημείο στο οποίο θα βρεθεί, να εκτελεί τη δεύτερη κίνηση - ανεξάρτητα από την πρώτη - επί τον ίδιο χρόνο t . Προσδιορίζεται έτσι το σημείο στο οποίο θα βρεθεί μετά χρόνο t.

Με καταλληλη επιλογή αξόνων – με βάση την πρακτική που μας δίδαξε ο Καρτέσιος – μπορούμε να δωσουμε την απάντηση για τη θέση της πέτρας με τις δύο συναρτήσεις

x= υ₀t και y = ½gt² και αν από τις δύο αυτές συναρτήσεις απαλείψουμε την t να έχουμε τη συνάρτηση y = σ ( x ) με την οποία προβλέπουμε τη μορφή της τροχιάς .

Η συνάρτηση y = gx²/2υ₀² δείχνει ότι η τροχιά θα είναι ΠΑΡΑΒΟΛΗ

2. Σχετική κίνηση – Σύστημα Αναφοράς

Ο Einstein για να περιγράψει παρόμοια φαινόμενα «εστίασε» περισσότερο στην έννοια

ΣΥΣΤΗΜΑ ΑΝΑΦΟΡΑΣ. Η δική του θεώρηση συνιστά και μια κάπως διαφορετική πρόταση η οποία εξυπηρετεί στο να 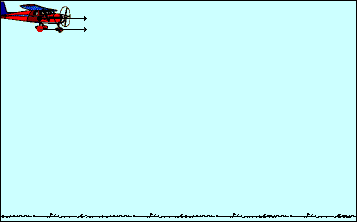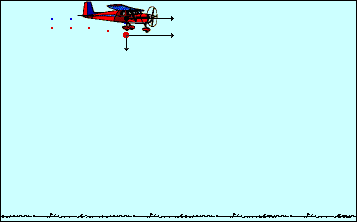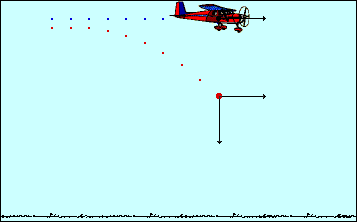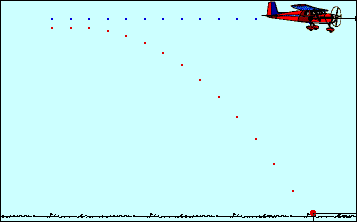δημιουργήσουμε «δικές μας εικόνες» για τις ΔΥΟ κινήσεις

Να φανταστούμε «πώς θα έβλεπε» την κίνηση της πέτρας ένας παρατηρητής Α κινούμενος οριζόντια σε αδρανειακό σύστημα με σταθερή ταχύτητα ίση με την – ως προς το έδαφος - αρχική ταχύτητα της πέτρας υ₀ . Θα διακρίνουμε ότι για τον παρατηρητή αυτόν η κίνηση της πέτρας είναι κατακόρυφη με επιτάχυνση της βαρύτητας, είναι μία ελεύθερη πτώση. Σαν αυτή που βλέπει ο πιλότος του αεροπλάνου αν αφήσει τη βόμβα και την παρατηρεί.

Μπορούμε επίσης να φανταστούμε «πώς θα έβλεπε» την κίνηση της πέτρας ένας παρατηρητής Β κινούμενος κατακόρυφα με την επιτάχυνση της βαρύτητας. Θα διακρίνουμε ότι η κίνηση – για τον παρατηρητή αυτόν - είναι οριζόντια ομαλή με την ταχύτητα εκτόξευσης υ₀ . Βέβαια ο παρατηρητής Β δεν είναι αδρανειακός και υπάρχει πρόβλημα στο να ΕΡΜΗΝΕΥΣΕΙ την κίνηση που παρατηρεί με τις γνωστές δυνάμεις. Αυτό όμως δεν εμποδίζει να τον επικαλεστούμε προκειμένου να ΠΕΡΙΓΡΑΨΟΥΜΕ την ως προς αυτόν ευθύγραμμη ομαλή κίνηση

Ο ίδιος ο Einstein έδωσε ιδιαίτερη σημασία σε ένα σύνολο εξισώσεων με τις οποίες ένας παρατηρητής σε αδρανειακό Σύστημα μπορεί να μεταφράζει στη δική του γλώσσα κάθε πληροφορία που φθάνει σε αυτόν απο ένα παρατηρητή σε άλλο Σύστημα. Τις εξισώσεις αυτές τις ονόμασε Μετασχηματισμούς του Γαλιλαίου αν και το «σχέδιο» ήταν να τις αμφισβητήσει, αντιπροτείνοντας κάποιες άλλες.

Με βάση τους μετασχηματισμούς του Γαλιλαίου

i . Σε σχέση με τον ΧΡΟΝΟ. Υπάρχει μία και μόνο τιμή του χρόνου για όλα τα αδρανειακά Συστήματα.

ii . Σχετικά με τη ΘΕΣΗ του αντικειμένου. Αν ένας αδρανειακός παρατηρητής, όπως ο Α, κινείται οριζόντια με ταχύτητα υ₀ – και θεωρήσουμε ένα ορθογώνιο σύστημα x, y , με αρχή αξόνων το σημείο εκτόξευσης του αντικειμένου και θετική φορά του y προς τα κάτω - ισχύει

x_σ,Α = x_σ,εδ – υ₀t y_σ,Α = y_{σ, εδ}

x_σ,Α και y_σ,Α είναι η οριζόντια και η κατακόρυφη μετατόπιση του αντικειμένου για τον παρατηρητή Α

x_σ,εδ και y_{σ, εδ} είναι οι αντίστοιχες μετατοπίσεις για παρατηρητή που βρίσκται στο έδαφος

και εφόσον o A αντιλαμβάνεται ότι x_σ,Α = 0 και y_σ,Α = ½ gt²

για ένα παρατηρητή στο έδαφος θα είναι x_σ,εδ = υ_οt και y_{σ, εδ} = ½gt²

Γενικότερα η τη σχετική θέση του σώματος ως προς οποιονδήποτε ΠΑΡΑΤΗΡΗΤΗ θα είναι η διανυσματική διαφορά της ( ως προς το έδαφος ) θέσης του σώματος r_σ μείον την (ως προς το έδαφος) θέση του παρατηρητή r_Π r_{σ, Π} = r_σ – r_Π οπότε και η ( ως προς το έδαφος ) θέση του σώματος θα είναι διανυσματικό άθροισμα r_σ = r_σ,Π + r_Π

Με τoυς ίδιους τρόπους – είτε ανάλυση της κίνησης είτε θεώρηση μέσα από αδρανειακό παρατηρητή - μπορούμε να προβλέπουμε την θέση και την τροχιά ενός ηλεκτρονίου το οποίο εκτοξεύεται κάθετα στις δυναμικές γραμμές ομογενούς ηλεκτρικού πεδίου.

Και είπε η μαθήτρια:

Πράγματι και τα δύο μας εξυπηρετούν στο να προβλέψουμε τη θέση του σώματος και τη μορφή της τροχιάς στην περίπτωση που η τροχιά είναι ΠΑΡΑΒΟΛΙΚΗ.

Θα μπορούσαμε άραγε να τα εφαρμόσουμε και για την πρόβλεψη θέσης και τροχιάς σε μια ΟΜΑΛΗ ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ ;

Δοκίμασα να το κάνω αλλά δεν ξέρω εάν είναι σωστό. Έφερα στο μυαλό μου ένα 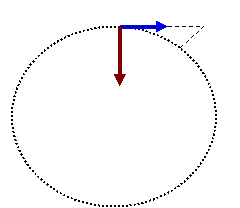σημειακό αντικείμενο το οποία να έχει ταχύτητα κάθετη στην ασκούμενη ολική δύναμη και να βρίσκεται σε περιβάλλον τέτοιο ώστε στη συνέχεια να εκτελεί ομαλή κυκλική κίνηση και δοκίμασα να προβλέψω τη θέση του με παρόμοιο τρόπο.

Η θέση του μετά χρόνο t μπορεί να προβλεφθεί εάν το φανταστώ

α. να εκτελεί επί χρόνο t την κίνηση Α, αυτή που θα εκτελούσε εάν δεν υπήρχε δύναμη – ευθύγραμμη ομαλή με ταχύτητα υ - και στη συνέχεια

β. επί τον ίδιο χρόνο t, την κίνηση που θα εκτελούσε εάν δεν υπήρχε ταχύτητα - κάθετα υπό την επίδραση μιας δύναμης F που να κατευθύνεται προς το κέντρο.

Με αυτό τον τρόπο μπορώ να προβλέψω ότι θα βρεθεί στο σημείο της κυκλικής τροχιάς στο οποίο τελικά βρίσκεται μετά χρόνο t . Κάνω κάποιο λάθος ;

Ποια είναι η καλύτερη απάντηση που θα μπορούσαμε να της δώσουμε ;

Ανδρέας Ιωάννου Κασσέτας