Ανδρέας Ιωάννου Κασσέτας

Και είπε η μαθήτρια:

Θα μπορούσαμε άραγε όλα αυτά να τα εφαρμόσουμε και για την πρόβλεψη θέσης και τροχιάς σε μια ΟΜΑΛΗ ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ ; Δοκίμασα να το κάνω αλλά δεν ξέρω εάν είναι σωστό. Έφερα στο μυαλό μου ένα σημειακό αντικείμενο το οποία να έχει ταχύτητα κάθετη στην ασκούμενη ολική δύναμη και να βρίσκεται σε περιβάλλον τέτοιο ώστε στη συνέχεια να εκτελεί ομαλή κυκλική κίνηση. Δοκίμασα να προβλέψω τη θέση του με παρόμοιο τρόπο.

Η θέση του μετά χρόνο t μπορεί να προβλεφθεί εάν το φανταστώ

α. να εκτελεί επί χρόνο t την κίνηση Α, αυτή που θα εκτελούσε εάν δεν υπήρχε δύναμη – ευθύγραμμη ομαλή με ταχύτητα υ - και στη συνέχεια

β. επί τον ίδιο χρόνο t, την κίνηση που θα εκτελούσε εάν δεν υπήρχε ταχύτητα υπό την επίδραση μιας δύναμης F που να κατευθύνεται προς το κέντρο.

Με αυτό τον τρόπο μπορώ να προβλέψω ότι θα βρεθεί στο σημείο της κυκλικής τροχιάς στο οποίο τελικά βρίσκεται μετά χρόνο t . Κάνω κάποιο λάθος ;

Αναρωτήθηκα επίσης «ποια θα είναι η τροχιά την οποία αντιλαμβάνεται ένας παρατηρητής κινούμενος με σταθερή ταχύτητα και δυσκολεύτηκα να τη φανταστώ».

Είπε τότε ο κύριος :

Ας δούμε το ζήτημα με προσοχή.

1. Ανάλυση σε δύο κάθετους άξονες.

Για να εφαρμόσουμ ε την Αρχή της Ανεξαρτησίας πρέπει να διακρίνουμε τις ΔΥΟ κινήσεις . Ποιες είναι όμως οι δύο ανεξάρτητες κινήσεις; Και εδώ «τα πράγματα είναι δύσκολα» και οπωσδήποτε διαφέρουν από την προηγούμενη περίπτωση της οριζόντιας βολής

Στην προηγούμενη περίπτωση εάν η αρχική ταχύτητα αλλάξει κατεύθυνση, το ΠΕΡΙΒΑΛΛΟΝ είναι τέτοιο ώστε η επίδρασή του να περιγράφεται με την ασκούμενη στο υλικό σημείο δύναμη οριζόντια και σταθερή . Κατά τον άξονα x δεν εμφανίζεται συνιστώσα, οπότε η λεγόμενη «κίνηση κατά τον άξονα x» είναι ευθύγραμμη ομαλή . Στην περιπτωση όμως μιας οποιασδήποτε ομαλής κυκλικής κίνησης το ΠΕΡΙΒΑΛΛΟΝ είναι τέτοιο ώστε η επίδρασή του στο κινούμενο υλικό σημείο να περιγράφεται με δύναμη η οποία -εκτός των άλλων- κατευθύνεται συνεχώς προς το ίδιο γεωμετρικό σημείο Κ.

Ας θεωρήσουμε δύο κάθετους αξονες x και y τεμνόμενους στο O, όπως στο σχήμα.

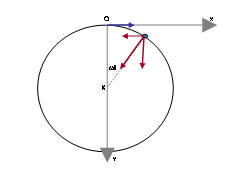Ας θεωρήσουμε ως αρχή των χρονων τη στιγμή που το υλικό σημείο Σ βρίσκεται στο σημείο Ο με ταχύτητα μέτρου υ – στο σχήμα οριζόντια - και η ασκούμενη σε αυτό δύναμη, κάθετη στην ταχύτητα, έχει μέτρο F₀ .

Στις στιγμές που θα ακολουθήσουν η ταχύτητα του Σ θα αλλάζει συνεχώς κατεύθυνση και η δύναμη κατευθυνόμενη προς το ίδιο πάντα σημείο Κ και διατηρούμενη κάθετη στην εκάστοτε ταχύτητα θα έχει και αυτή αδιάκοπα μεταβαλλόμενη κατευθυνση . Τη χρονική στιγμή t το διάνυσμα της ταχύτητας θα έχει στραφεί κατά ωt και το διάνυσμα της δύναμης θα έχει και αυτό στραφεί κατά την ίδια γωνία .

Αυτό σημαίνει ότι η σταθερού μέτρου αυτή δύναμη θα έχει – κατά τον άξονα x - συνιστώσα , κατευθυνόμενη προς το σημείο Ο μέτρου |F₀x/R|

Η μία κίνηση – στον άξονα x - θα είναι κίνηση ενός υλικού σημείου με αρχική ταχύτητα υ στο οποίο ασκείται δύναμη επαναφοράς μέτρου |F₀x/R| ή αλγεβρικής τιμής (σε σχέση με συγκεκριμένο άξονα) -F₀x/R . Θα είναι συνεπώς αρμονική ταλάντωση με συχνότητα τη συχνότητα της κυκλικής κινησης, με θέση ισορροπίας το Ο και με μέγιστη ταχύτητα ωR, άρα ταλάντωση με πλάτος R.

Για τη θέση του σωματιδίου θα ισχύει x = Rημωt .

H άλλη κίνηση, στο άξονα y, θα είναι κίνηση με μηδενική αρχική ταχύτητα υ και με ασκούμενη δύναμη αρχικά μέτρου F₀ κατευθυνόμενη προς το σημείο Κ η οποία στη συνέχεια θα έχει μέτρο |F₀x/R|. Θα είναι και αυτή αρμονική ταλάντωση ίδιας συχνότητας πλάτους R άρα με θέση ισορροπίας το κέντρο του κύκλου Κ.

Η θέση (απομάκρυνση) του Σ, με συγκεκριμένη επιλογή του άξονα και ως προς τη «δική του» θέση ισορροπίας την Κ,

θα είναι ίση με Rημ(ωt+π/2) = Rσυνωt.

Τη χρονική στιγμή t το κινούμενο Σ λόγω της κατά τον x ταλάντωσης θα απέχει από το Ο

Rημωt, και λόγω της κατά τον y ταλάντωσης θα απέχει από το Ο R-Rσυνωt.

Μπορούμε συνεπώς να δεχθούμε κάθε ομαλή κυκλική κίνηση αναλύεται

σε δύο αρμονικές ταλαντώσεις κάθετες μεταξύ τους

και να ΠΡΟΒΛΕΨΟΥΜΕ τη θέση του Σ μετά χρόνο t αρκεί να το φανταστούμε να εκτελεί

α. τη μία ταλάντωση επί χρόνο t οπότε θα έχει απομακρυνθεί οριζόντια από το Ο κατά x = R ημωt και στη συνέχεια β. να εκτελεί την άλλη ταλάντωση επί χρονο t οπότε θα έχει μετατοπιστεί κατακόρυφα κατά y = R- Rσυνωt . Θα βρεθεί έτσι σε σημείο Λ με συντεταγμένες

x = R ημωt y = R - Rσυνωt . Με απαλοιφή του t προκύπτει x ² + (R – y)² = R² και αυτό επιβεβαιώνει ότι το σύνολο των σημείων στα οποία θα βρεθεί θα είναι σημεία συγκεκριμένου κύκλου.

2. Σχετική κίνηση – Σύστημα Αναφοράς

Ένας άλλος τρόπος για να δημιουργήσουμε «δικές μας εικόνες» για τις ΔΥΟ κινήσεις είναι να χρησιμοποιήσουμε την έννοια ΣΥΣΤΗΜΑ ΑΝΑΦΟΡΑΣ.

Να φανταστούμε πώς θα έβλεπε την κίνηση του υλικού σημείου Σ ένας παρατηρητής Π κινούμενος οριζόντια με σταθερή ταχύτητα ίση με την ταχύτητα του σωματιδίου στην αρχή των χρόνων. Είναι δύσκολο να το φανταστούμε. Στην αρχή των χρόνων το σωματίδιο έχει σχετική – ως προς αυτόν- ταχύτητα μηδέν. Σε χρόνο μιας περιόδου ο παρατηρητής θα έχει μετακινηθεί οριζόντια ως προς το έδαφος κατά υΤ = 2πR άρα το Σ θα έχει απομακρυνθέι από αυτόν κατά 2πR και θα έχει ως προς αυτόν και πάλι ταχύτητα μηδέν. Σε χρόνο μισής περιόδου η σχετική ταχύτητα του Σ θα είναι 2υ.

Με βάση τους Μετασχηματισμούς του Γαλιλαίου η ( σχετική ) θέση του σημειακού αντικειμένου σ ως προς οποιονδήποτε ΠΑΡΑΤΗΡΗΤΗ π θα είναι η διανυσματική διαφορά της ( ως προς το έδαφος ) θέσης του Σ μείον την ( ως προς το έδαφος) θέση του παρατηρητή r_{σ, π} = r_σ – r_π , σχέση στην οποία

τα r_{σ, π} , r_σ , r_π είναι διανύσματα .

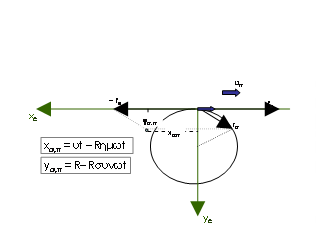
Με κατάλληλη επιλογή αξόνων x_c και y_c – όπως στο σχήμα - για τη σχετική θέση του Σ προκύπτει

x_Σ,π = ωRt – Rημωt και y_Σ,π = R – R συνωt.

Οι εξισώσεις αυτές οδηγούν στο συμπέρασμα ότι

η τροχιά την οποία αντιλαμβάνεται ο αδρανειακός παρατηρητής είναι ΚΥΚΛΟΕΙΔΗΣ, με τα κοίλα προς τα πάνω .

Το «γιατί» καταλήγουμε σε αυτό το συμπέρασμα θα το δούμε παρακάτω.

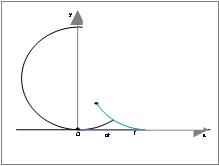
Κυκλοειδής . Η κυκλοειδής είναι η τροχιά ενός υλικού σημείου κάθε τροχού που κυλάει σε οριζόντιο έδαφος χωρίς να ολισθαίνει. Φανταζόμαστε έναν τροχό κυλιόμενο σε οριζόντιο έδαφος έτσι ώστε το κέντρο μάζας να έχει σταθερή ταχύτητα υ. Θεωρούμε το σημείο της περιφέρειας του τροχού το οποίο σε κάποια χρονική στιγμή – αρχή των χρόνων- βρίσκεται στην κατώτερη θέση 0 . Η θέση του μετά χρόνον t μπορεί να προβλεφθεί εάν το φανταστούμε επί χρόνο t να κινείται σύμφωνα με τη μεταφορική κίνηση του τροχού ευθύγραμμα με σταθερή ταχύτητα υ ( οπότε προσδιορίζεται το σημείο Γ με ΟΓ = ωRt και στη συνέχεια από το σημείο Γ να εκτελεί την κυκλική κίνηση –σύμφωνα με τη στροφική κίνηση – επί τον ίδιο χρόνο διαγράφοντας ένα τόξο γωνίας ωt ίσου μήκους με εκείνο του ΟΓ. Το σημείο Δ στο οποίο θα βρεθεί είναι ακριβώς το σημείο στο οποίο θα βρίσκεται κάνοντας την ελικοειδή κίνηση μετά χρόνον t. Με σύστημα αξόνων κάθετων αξόνων με αρχή το Ο, για τη θέση του Δ έχουμε

x = ωRt – Rημωt και y = R – Rσυνωt.

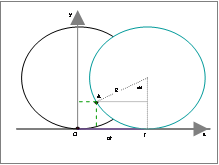
Από τις παραμετρικές αυτές συναρτήσεις απορρέει dx/dt = ωR–ωRσυνωt και dy/dt = Rημωt οπότε και η

(dy/dx)² =( 2R-y)/y η οποία είναι η διαφορική εξίσωση της κυκλοειδούς. Στην προκειμένη περίπτωση αυτό δεν μας ενδιαφέρει.

Επιστρέφουμε στο αρχικό σύστημα και μπορούμε να φανταστούμε

το κυκλικά κινούμενο σωματίδιο να εκτελεί

α. την ευθύγραμμη ομαλή κίνηση επί χρόνο t

και στη συνέχεια

β. την κυκλοειδή, με μηδενική αρχική ταχύτητα και επί χρόνο t,

οποτε θα προβλέψουμε τη θέση του.

Θα βρεθεί έτσι σε σημείο με συντεταγμένες

x = R ημωt y = R - Rσυνωt .

Με απαλοιφή του t προκύπτει x ² + (R – y)² = R²

και αυτό επιβεβαιώνει ότι το σύνολο των σημείων στα οποία θα βρεθεί θα είναι σημεία κύκλου.

Πρέπει να παρατηρήσουμε ότι αυτό που κάνουμε είναι – σε μια άλλη ανάγνωση –

το ότι φανταζόμαστε το Σ να εκτελεί τρεις κινήσεις. Επί χρόνο t μία ευθύγραμμη προς τα δεξιά με ταχύτητα υ,

επί χρόνο t μία ευθύγραμμη προς τα αριστερά με αντίθετη ταχύτητα μέτρου υ και,

επί τον ίδιο χρόνο t, μία κυκλική όπως η αρχική οπότε εύλογα το Σ

βρίσκεται στο σημείο που θα βρισκόταν εκτελώντας μόνο την κυκλική επί χρόνο t.

Το ενδιαφέρον της συγκεκριμένης προσέγγισης είναι η απόδειξη

του ότι «εαν ένα αντικείμενο κινείται κυκλικά με ταχύτητα υ,

η σχετική κίνησή του – για καθε αδρανειακό παρατηρητή κινούμενο με ταχύτητα υ

στο επίπεδο του κύκλου - είναι ΚΥΚΛΟΕΙΔΗΣ».

Σκέψεις για τη διδασκαλία. Η διδακτική αξιοποίηση της έννοιας Σύστημα Αναφοράς συνήθως αγνοείται

κατά τη διδασκαλία μας, ενώ θα μπορούσε να χρησιμοποιηθεί κατά την εξέλιξη , λόγου χάρη,

του φαινομένου κύλιση, με το να «διακρίνει» κάποιος την «άλλη» κίνηση

θεωρώντας ότι η «μία» είναι μεταφορική με την ταχύτητα του κέντρου μάζας

Στα πλαίσια βέβαια του ισχύοντος Αναλυτικού προγράμματος – στο οποίο δεν διδάσκεται η έννοια

σχετική ταχύτητα και «εμφανίζεται ξαφνικά» κατά την απόδειξη στο φαινόμενο Doppler-

το Σύστημα αναφοράς, έαν χρησιμοποιηθεί, πρέπει να είναι αδρανειακό . Και αυτό διότι σε διαφορετική περιπτωση

δεν αρκούν οι «γνωστές» δυνάμεις για την περιγραφή και την ερμηνεία της σχετικής κίνησης.

Αξίζει να σημειώσουμε ότι

αν ένας τροχός κυλίεται σε οριζόντιο έδαφος ,

η σχετική κίνηση ενός σημείου Σ μιας κατακόρυφης περιφέρειας είναι

α. ως προς το έδαφος ΚΥΚΛΟΕΙΔΗΣ .

β. ως προς αδρανειακό παρατηρητή -κινούμενο με την ταχύτητα υ του κέντρου μάζας- ΚΥΚΛΙΚΗ

Σχόλια μόνο για φυσικούς.

α. Η λεγόμενη «Αρχή της ανεξαρτησίας των κινήσεων «κατάγεται» από

μία ιδέα του Γαλιλαίου και αφορά μόνο στο φαινόμενο κίνηση.

β. Στα χρόνια που ακολούθησαν μια ιδέα παρόμοιας λογικής οδήγησε

στη γενικότερη Superposition Rrinciple, Αρχή της υπέρθεσης, η οποία πέραν του φαινομένου κίνηση

– αξιοποιήθηκε και σε άλλα ζητήματα – συμβολή των κυμάτων, ανάλυση Fourier, ηλεκτρικά κυκλώματα-

– υπό την προϋπόθεση οι διαφορικές εξισώσεις που τα περιγράφουν να είναι γραμμικες.

– γ. Η Αρχή χωρίς να αποτελεί κάποιο ξεχωριστό νόμο της Φυσικής, συνιστά μία γόνιμη τεχνική για ορισμένες

– περιπτώσεις κινήσεων. Τo ζήτημα που τίθεται είναι «εάν οι δύο κινήσεις είναι ανεξάρτητες» και αυτό

– σε ορισμένες περιπτώσεις είναι απλό αλλά σε άλλες δεν είναι. Χρειάζεται σε καθεμιά από τις αναλυτικές εξισώσεις

– που μας δίνει η αντίστοιχη διαφορική να μην υπεισέρχονται οι μεταβλητές θέσης και ταχύτητας μιας άλλης.

Και είπε (;) η μαθήτρια:

Κατάλαβα ότι η αρχική μου ιδέα να προβλέπω τη θέση μέσα από μία ευθύγραμμη ομαλή κίνηση και στη συνέχεια

μία ευθύγραμμη κίνηση προς το κέντρο του κύκλου, δεν ευσταθεί

Κατάλαβα επίσης ότι για να προβλέπω τη θέση ενός σημειακού αντικειμένου στο μέλλον, μπορώ να εμπιστεύομαι

την Αρχή της Ανεξαρτησίας, μόνο αν είμαι σίγουρη ότι οι δύο κινήσεις είναι ΑΝΕΞΑΡΤΗΤΕΣ .

Κατάλαβα τέλος ότι αν η μία κίνηση αν θέλω να διακρίνω τις δύο κινήσεις στις οποίες θα μπορούσα να αναλύσω

την κίνηση ενός Σ -το οποίο σε κάποια στιγμή έχει ταχύτητα υ- μπορώ να φαντάζομαι τον εαυτό μου

σε σύστημα αναφοράς κινούμενο με την ταχύτητα υ και να διακρίνω τη σχετική κίνηση του Σ.

Η μία κίνηση θα είναι η ομαλή με ταχύτητα υ και η «άλλη» θα είναι η σχετική κίνηση την οποία μπόρεσα να διακρίνω

Αλλά στην περίπτωση ΟΜΑΛΗΣ ΚΥΚΛΙΚΗΣ ΚΙΝΗΣΗΣ τα πράγματα γίνονται αρκετά δύσκολα

για μένα και θα προτιμούσα να αποφύγω τόσο τη μέθοδο που οδηγεί σε δύο κάθετες ταλαντώσεις

όσο και την άλλη που οδηγεί σε ευθύγραμμη και κυκλοειδή.

Η ωραία Ελένη της Γεωμετρίας .

Ο Γαλιλαίος ήταν εκείνος που της έδωσε το όνομα . H ΚΥΚΛΟΕΙΔΗΣ καμπύλη με «φοβερά προσόντα» προκάλεσε το ενδιαφέρον των μαθηματικών του 17^ου αιώνα αλλά σοβαρές διενέξεις αναφορικά με αποδείξεις για τις ιδιότητές της. Την χαρακτηρίζουν «ωραία Ελένη» της Γεωμετρίας.

Αν είναι R η ακτίνα του κύκλου από τον οποίο προκύπτει, το ύψος της είναι ίσο με 2R. Από τον 17^ο αιώνα απέδειξαν ότι το εμβαδόν της είναι ίσο με 3πR² και ότι το μηκος του τόξου της είναι ίσο 8R. Ανάμεσα στις ιδιότητες που την κάνουν να θεωρείται «καμπύλη με φοβερά προσόντα» συγκαταλέγονται

1. Αν αφήσουμε οσεσδήποτε μπίλιες να κινηθούν με τη βαρύτητα σε κατακόρυφη στερεά επιφάνεια χωρίς τριβή σε περίπτωση που το σχήμα – η κατακόρυφη τομή - της επιφάνειας είναι κυκλοειδές φθάνουν οι μπίλιες ΤΑΥΤΟΧΡΟΝΑ

από οποιοδήποτε σημείο κι αν τις αφήσουμε .

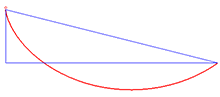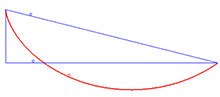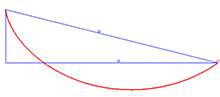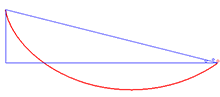
2. Για να κινηθεί μια μπίλια από ένα σημείο Α σε ένα σημείο Β χαμηλότερα χωρίς τριβή σε οδηγούς διαφόρων σχημάτων ο πιο γρήγορος δρομος είναι ο δρόμος της κυλκλοειδούς.

3. Σε κάθε σημείο μιας καμπύλης ( έλλειψη , παραβολή, υπερβολή, κυκλοειδής και όχι μόνο) αντιστοιχεί ένα κέντρο καμπυλότητας. Αν ένα σημειακό αντικείμενο σημείο κινείται σε μια καμπύλη το κέντρο καμπυλότητας διαγράφει μια άλλη γραμμή. Αν η αρχική καμπύλη είναι έλλειψη η γραμμή την οποία διαγράφει το κέντρο καμπυλότητας δεν είναι έλλειψη . Αυτη η διαφορετικότητα ισχύει και για όλες τις άλλες καμπύλες – όπως η παραβολή , η υπερβολή, η καρδιοειδής και όχι μόνο - εκτός από μία. Και η ΜΙΑ καμπύλη η οποία συνιστά τη μοναδική εξαίρεση είναι η κυκλοειδής. Η διαγραφόμενη από το κέντρο καμπυλότητας γραμμή είναι κυκλοειδής ίδια ακριβώς με την αρχική .

Αξιόλογες παρουσιάσεις της κυκλοειδούς καμπυλης έχουν κάνει αρκετοί συνάδελφοι στο διαδίκτυο. Ανάμεσά τους, δύο από τους πρώτους που διέκριναν την ομορφιά της «ωραίας Ελένης» είναι ο Πάνος Μουρούζης στο site του ΕΚΦΕ Κέρκυρας και ο Νίκος Δαπόντες στον δικό του δικτυακό τόπο.