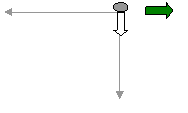
1. Οι σταγόνες της βροχής πέφτουν κατακόρυφα με σταθερή – ορική - ταχύτητα .

Πώς αντιλαμβάνεται τη βροχή κάποιος χωρίς ομπρέλα ;

Τόσο για τη σταγόνα σ όσο και γαι τον παρατηρητή π

επιλέγω χωρικό σύστημα αναφοράς με άξονα x με το + προς τα αριστερά και τον y με το + προς τα κάτω

και χρονικό σύστημα αναφοράς με Αρχή των χρόνων τη στιγμή που τόσο το αντικείμενο/σταγόνα σ

κινούμενο ως προς το έδαφος με σταθερή ταχύτητα μέτρου υ_σ , όσο και ο παρατηρητής

κινούμενος ως προς το έδαφος με οριζόντια σταθερή ταχύτητα μέτρου υ_π ,

βρίσκονται στην αρχή των αξόνων Ο, οπότε, κατά τη χρονική στιγμή t :

Για την, ως προς το έδαφος, θέση του αντικειμένου ( τα σύμβολα παριστάνουν αλγεβρικές τιμές )

x_σ = 0 y_σ = υ_σt

Για την, ως προς το έδαφος, θέση του παρατηρητή

x_π = - υ_πt y_π = 0

Για την, ως προς τον παρατηρητή, θέση του αντικειμένου

x_σπ = x_Σ – x_π y_σπ = y_Σ – y_π

x_σπ = υ_πt y_σπ = υ_σt

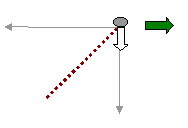
Η σχετική κίνηση είναι μια κίνηση ευθύγραμμη ομαλή

y_σπ = x_σπ (υ_σ/υ_π)

(εξίσωση της τροχιάς)

Η τροχιά της σχετικής κίνησης

είναι ευθύγραμμη

και σχηματίζει με το έδαφος γωνία θ με εφθ = υ_σ/υ_π

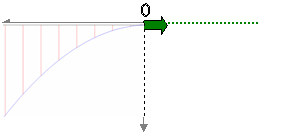
2. Το αντικείμενο Σ αφήνεται να πέσει προς το έδαφος. Αντίσταση του αέρα αμελητέα

Πώς βλέπει την τροχιά του κάποιος που κινείται με οριζόντια ταχύτητα μέτρου υ_π ;

Επιλέγω χωρικό σύστημα αναφοράς, έτσι ώστε ο με άξονα x με το + προς τα αριστερά

και τον y με το + προς τα κάτω και αρχή το σημείο Ο που εκτοξεύεται το αντικείμενο Σ

και χρονικό σύστημα αναφοράς με Αρχή των χρόνων τη στιγμή της εκτόξευσης, οπότε :

Για την, ως προς το έδαφος, θέση του αντικειμένου

x_Σ = 0 y_Σ =½gt²

Για την, ως προς το έδαφος, θέση του παρατηρητή

x_π = - υ_πt y_Σ = 0

Για την, ως προς τον παρατηρητή, θέση του αντικειμένου

x_Σπ = x_Σ – x_π y_Σπ = y_Σ – y_π

( τα σύμβολα παριστάνουν αλγεβρικές τιμές )

x_Σπ = υ_πt y_Σπ = ½gt²

y_Σπ = ½g x_Σπ² /υ_π²(εξίσωση της τροχιάς)

Η σχετική κίνηση

του αντικειμένου ως προς τον παρατηρητή

είναι κίνηση σε τροχιά παραβολική

3. Το αντικείμενο Σ εκτοξεύεται κατακόρυφα προς τα πάνω με ταχύτητα υ₀.

Αντίσταση του αέρα αμελητέα

α. Πώς βλέπει την κίνηση του Σ ένας παρατηρητής που κινείται – εννοείται ως προς το έδαφος –

κατακόρυφα προς τα πάνω με σταθερή ταχύτητα μέτρου υ₀ ;

Επιλέγω χωρικό σύστημα αναφοράς με άξονα x και τον y με το + προς τα πάνω

και αρχή το σημείο Ο που εκτοξεύεται το αντικείμενο Σ

και χρονικό σύστημα αναφοράς με Αρχή των χρόνων τη στιγμή της εκτόξευσης, οπότε :

Για την ως προς το έδαφος θέση του αντικειμένου x_Σ = 0 y_Σ = υ₀t - ½|g|t²

Για την ως προς το έδαφος θέση του παρατηρητή x_π = 0 y_π = υ₀t

Για την ως προς τον παρατηρητή θέση του αντικειμένου

x_Σπ = x_Σ – x_π y_Σπ = y_Σ – y_π

x_Σπ = 0 y_Σπ = - ½|g|t²

Η σχετική κίνηση του αντικειμένου ως προς τον παρατηρητή

είναι κίνηση προς τα κάτω σε ευθύγραμμη τροχιά με την επιτάχυνση της βαρύτητας

β. Πώς βλέπει την τροχιά του Σ ένας άλλος παρατηρητής που κινείται οριζόντια με σταθερή ταχύτητα μέτρου υ₀ ;

Επιλέγω χωρικό σύστημα αναφοράς με άξονα x (με το + προς τα αριστερά ) και y με το + προς τα πάνω

και αρχή το σημείο Ο που εκτοξεύεται το αντικείμενο Σ

και χρονικό σύστημα αναφοράς με Αρχή των χρόνων τη στιγμή της εκτόξευσης, οπότε :

Για την, ως προς το έδαφος, θέση του αντικειμένου x_Σ = 0 y_Σ = υ₀t - ½|g|t²

Για την, ως προς το έδαφος, θέση του παρατηρητή x_π = - υ₀t y_π = 0

Για την, ως προς τον παρατηρητή, θέση του αντικειμένου

x_Σπ = x_Σ – x_π y_Σπ = y_Σ – y_π

x_Σπ = υ₀t y_Σπ = υ₀t - ½|g|t²

y_Σπ = x_Σπ - ½|g|x_Σπ²/υ₀² (εξίσωση της τροχιάς)

Η σχετική κίνηση του αντικειμένου ως προς τον παρατηρητή

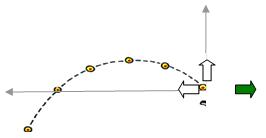είναι κίνηση σε τροχιά παραβολική.

Η σχετική ταχύτητα στην αρχή των χρόνων

έχει δύο κάθετες συνιστώσες

ίσων μέτρων άρα

σχηματίζει γωνία 45⁰

με τον ορίζοντα.

4. Το αντικείμενο σ εκτελεί αρμονική ταλάντωση

με μέγιστη ταχύτητα υ . Πώς βλέπει την τροχιά του σ

κάποιος που κινείται με ταχύτητα μέτρου υ

κάθετη στην τροχιά της ταλάντωσης

Έστω ότι η , ως προς το έδαφος, ταλάντωση του σ εκτελείται με πλάτος Α και γωνιακή συχνότητα ω

και ότι η, ως προς το έδαφος, σταθερή ταχύτητα του παρατηρητή π έχει μέτρο ωΑ .

Επιλέγω: α. Χωρικό σύστημα αναφοράς με άξονες x και y, όπως στο σχήμα, με Αρχή τη θέση τη ισορροπίας Ο του ταλαντωτή.

β. Χρονικό σύστημα αναφοράς με Αρχή των χρόνων τη χρονική στιγμή που ο ταλαντωτής σ βρίσκεται στη θέση Ο με ταχύτητα -ως προς το έδαφος - υ_σ και θετική ως προς τον άξονα y, και ο παρατηρητής π βρίσκεται στο ίδιο σημείο Ο με ταχύτητα -ως προς το έδαφος - υ_π κάθετη στον y και, ως προς τον x, αρνητική . υ_π= - ωΑ

Για τις αλγεβρικές τιμές της σχετικης θέσης του σ είναι

x_σ,π = x _σ – x _π x_σ,π = - υ_πt και εφόσον υ_π=-ωΑ x_σ,π = ωΑt (1)

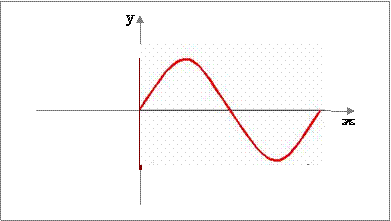
y_σ,π = y_σ – y_π y_σ,π = Aημ(ωt) (2)

Με απαλοιφή του t από τις (1) και (2)

y_σ,π = Aημ (x_σ,π /A)

Συμπεραίνω ότι η σχετική κίνηση του σ

γίνεται σε τροχιά «χωρικά ημιτονοειδή»

.