Ανδρέας Ιωάννου Κασσέτας

Οι ΑΠΑΝΤΗΣΕΙΣ στα ερωτήματα 1 έως 16

1. Η μαθήτρια, η άνωση και το αεικίνητο .

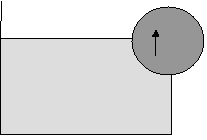Η μαθήτρια παίρνει μια κιμωλία και κάνει ένα σχήμα στον πίνακα. Ένα δοχείο με νερό

και ένας τροχός με στερεωμένο το κέντρο του, τοποθετημένος έτσι ώστε το «ένα τέταρτο» να διατηρείται κατάλληλα μέσα στο νερό Αν καταφέρω να κάνω αυτή την κατασκευή κυρία, η άνωση που θα ασκείται στο βυθισμένο τμήμα του θα κάνει τον τροχό να στρέφεται συνεχώς χωρίς να σταματάει.

Νομίζω ότι ανακάλυψα ένα αεικίνητο .

1. Συνήθως δεν δίνουμε έμφαση στο ότι

α. η άνωση είναι η συνισταμένη των πιεστικών δυνάμεων που ασκεί το υγρό σε κάθε σημείο της επιφάνειας του «επισκέπτη» και στο ότι

β. οι πιεστικές δυνάμεις είναι εξ ορισμού ΚΑΘΕΤΕΣ στην επιφάνεια στην οποία ασκούνται . Στην περίπτωση του τροχού, η συνισταμένη των πιεστικών δυνάμεων δεν είναι κατακόρυφη. Όλες οι ασκούμενες από το νερό πιεστικές δυνάμεις κατευθύνονται στο κέντρο του τροχού και δεν δημιουργείται ροπή οπότε και ο αρχικά ακίνητος τροχός δεν πρόκειται να περιστραφεί

2. Ο φελλός ανεβαίνει επειδή υπάρχει βαρύτητα

Ρώτησαν ένα φυσικό «γιατί ανεβαίνει ο φελλός, αν τον βάλουμε στο νερό και τον αφήσουμε ;» κι εκείνος απάντησε ότι «ανεβαίνει επειδή υπάρχει βαρύτητα» . Τι εννοούσε ;

2. Η ύπαρξη βαρύτητας δημιουργεί ολοένα και μεγαλύτερη πίεση στο νερό καθώς κατεβαίνουμε προς τα κάτω. Η μεγαλύτερη τιμή πίεσης στη βάση του φελλού συνεπάγεται μεγαλύτερη τιμή πιέζουσας δύναμης σε σχέση με εκείνη που ασκείται στο πάνω μέρος του φελλού άρα δημιουργεί άνωση. Ο φελλός ανεβαίνει στο νερό «επειδή υπάρχει βαρύτητα». Εξάλλου χωρίς βαρύτητα δεν θα υπήρχαν οι χωρικές έννοιες πάνω και κάτω, τα ρήματα ανεβαίνω και κατεβαίνω, ούτε και η έννοια άνωση .

3. Η βάρκα , η κοπέλα και η πέτρα .

Η βάρκα με την κοπέλα και την πέτρα επιπλέουν στο νερό της πισίνας. Σε κάποια στιγμή η κοπέλα παίρνει την πέτρα, την βάζει στο νερό και την αφήνει να βυθιστεί. Θα ανέβει, θα κατέβει ή θα μείνει σταθερή η στάθη του νερού ;

3. Η στάθμη θα κατέβει, αν και ελάχιστα. Πάντως θα κατέβει

Ας συμβολίσουμε με Η₁ και Η₂ το ύψος της στάθμης, με S το εμβαδόν της βάσης της πισίνας , με V_νερ τον όγκο του νερού και

με V_1εκ , V_2εκ , το εκτόπισμα της βάρκας με ότι περιέχει, αρχικά και τελικά .

Αρχικά . Η ισορροπία της βάρκας με την πέτρα: (Μ+m)g = ρgV_1εκ Η Γεωμετρία: SH₁ = V_νερ + V_1εκ

Αφού βυθιστεί η πέτρα . Η ισορροπία της βάρκας χωρίς την πέτρα: Μg = ρgV_2εκ Η Γεωμετρία: SH₂ = V_νερ + V_2εκ

Από τις εξισώσεις προκύπτει ότι H₁ - H ₂ = 1/S ( m/ρ - m/ρ_π )

Με Μ συμβολίζεται η μάζα βάρκας και κοπέλας με ρ η πυκνότητα του νερού, με m η μάζα της πέτρας και με ρ_π η πυκνότητα της πέτρας

4. Γιατί κρυώνω ; Θερμότητα ή ακτινοβολία ;

Γιατί κρυώνω όταν βρεθώ χωρίς ρούχα στο ύπαιθρο ; Οφείλεται στη ΘΕΡΜΟΤΗΤΑ που μεταβιβάζεται από το σώμα μου ή στο ότι η ΑΚΤΙΝΟΒΟΛΙΑ που εκπέμπει το σώμα μας είναι περισσότερη από την ακτινοβολία που απορροφά ;

4. Ο άνθρωπος κρυώνει όταν μεταβιβάζει ενέργεια ( περισσοτερη από όση του μεταβιβάζεται) είτε με μηχανισμό ΘΕΡΜΟΤΗΤΑΣ είτε με μηχανισμό ακτινοβολίας ΑΚΤΙΝΟΒΟΛΙΑΣ. Κάθε σώμα εκπέμπει υπέρυθρη ΑΚΤΙΝΟΒΟΛΙΑ . Ταυτόχρονα το ανθρώπινο σώμα μεταβιβάζει ενέργεια στον συνήθως χαμηλότερης θερμοκρασίας περιβάλλοντα αέρα με μορφή ΘΕΡΜΟΤΗΤΑΣ.

Η ροή θερμότητας έχει ως αιτία τη διαφορά των θερμοκρασιών και γίνεται πάντα από το σώμα ψηλότερης θερμοκρασίας προς το σώμα με τη χαμηλότερη, ενώ η εκπομπή ακτινοβολίας δεν προϋποθέτει διαφορά θερμοκρασιών και γίνεται από κάθε σώμα με μη μηδενική απόλυτη θερμοκρασία. Η ανά μονάδα χρόνου και ανά μονάδα επιφάνεια εκπεμπόμενη ενέργεια ακτινοβολίας είναι ανάλογη με την τέταρτη δύναμη της θερμοκρασίας. Το μεγαλύτερο μερος των θερμικών απωλειών του ανθρώπινου σώματος, όταν δεν υπάρχει αέρας, οφείλεται στη εκπεμπόμενη από αυτό θερμική ακτινοβολία εφόσον αυτή υπερισχύει της ακτινοβολίας που δέχεται.

Όταν υπάρχει αέρας το αν και πόσο θα κρυώσουμε καθορίζεται από τους συσχετισμούς ακτινοβολίας και θερμότητας.

5. Ο αστροναύτης και το θερμόμετρο.

Η θερμοκρασία του αέρα σχετίζεται μόνο με τη μέση κινητική ενέργεια των σωματιδίων του αέρα. Τι συμβαίνει σε περιοχές που δεν υπάρχει αέρας ; Ο αστραναύτης βγαίνει από το σκάφος και μετακινείται στο διάστημα έχοντας μαζί του κι ένα θερμόμετρο. Συμβαίνει ροή ενέργειας με μηχανισμό θερμότητας ; Τι δείχνει το θερμόμετρο;

5. Εφόσον δεν υπάρχει αέρας το μέγιστο των ενεργειακών ανταλλαγών για κάθε αντικείμενο , είτε ανθρώπινο σώμα είτε θερμόμετρο, σχετίζεται με ΑΚΤΙΝΟΒΟΛΙΑ. Εφόσον η εκπεμπόμενη από το σώμα ακτινοβολία – η οποία εκπέμπεται ανεξάρτ ητα από το «πως είναι το περιβάλλον» – υπερισχύει της ακτινοβολίας που προσπίπτει σε αυτό η θερμοκρασία του ελαττώνεται. Όσο για το θερμόμετρο αυτό που δείχνει είναι, όπως πάντα, η θερμοκρασία του.

6. Χιόνι και Γεωμετρία

Τότε στην Αράχωβα, εκείνος και μια νιφάδα χιονιού μπροστά στα μάτια του . Έχει μόλις προσγειωθεί στο παρμπρίζ ενός αυτοκινήτου και διακρίνει ότι μπορεί να δείχνει διαφορετική από τις άλλες νιφάδες αλλά προσέχει ότι ολες έχουν έξι πλευρές, είναι κάτι σαν εξάγωνα, μια γεωμετρική αρχιτεκτονική που τον βάζει σε σκέψεις.

6. Το χιόνι είναι νερό σε ορισμένη κατάσταση . Με την ψύξη τα νερού τα μόρια σχεδόν ακινητοποιούνται σε σχετικά στεθερές αποστάσεις μεταξύ τους. Στις αρχές του 20^ου αιώνα οι ακτίνες Χ αποδείχτηκαν εκπληκτικό εργαλείο που μας αποκάλυπτε την αρχιτεκτονική του Μικροκοσμου των στερεών . Στην περίπτωση του παγωμένου νερού η «εικόνα» παρουσίαζε ένα επαναλαμβανόμενο σχέδιο με εξάγωνα - κρυστάλλους , σε επίπεδο Μικρόκοσμου - σε κάθε κορυφή του κάθε εξαγώνου κι από ένα μόριο και τα εξάγωνα αυτά με τη σειρά τους να συνδέονται με άλλα μόρια νερού παρόμοιας δομής, δίπλα, πάνω και κάτω. Σε κλίμακα Μικρόκοσμου ο σωρός των μορίων του παγωμένου νερού μοιάζει με κηρήθρα. Σε αυτό το μοριακό συγκρότημα βρίσκεται και η απάντηση για τη μορφή των νιφάδων.

Σε κατάλληλες ατμοσφαιρικές συνθήκες, ένας κρύσταλλος θρονιάζεται σε κάποιο σωματίδιο σκονης και αρχίζει να αυξάνεται με την προσθήκη μορίων νερού στα άκρα του, διατηρώντας όμως πάντα το εξαγωνικό σχήμα. Σιγά σιγά μεγαλώνει τόσο ώστε να μπορεί κανείς να διακρίνει μια νιφάδα χιονιού.

7. Τραβάει απότομα το τραπεζομάντηλο

Τραβάει αργά το τραπεζομάντηλο και το πιάτα «έρχονται μαζί» .

Το τραβάει απότομα και τα πιάτα μενουν στη θέση τους.

Τι λένε γι αυτό οι φυσικοι ;

7. Το «πόσο απότομα» τραβάει εκείνος το τραπεζομάντηλο, οι φυσικοί το ποσοτικοποιούν με την έννοια επιτάχυνση.

Καθώς τραβάει αργά το τραπεζομάντηλο το πιάτο «έρχεται μαζί», με την ίδια δηλαδή επιτάχυνση που έχει και το τραπεζομάντηλο.

Η ολική οριζόντια δύναμη είναι η στατική τριβή και σύμφωνα με τον δεύτερο νόμο η τιμή της σχετίζεται με την τιμή της επιτάχυνσης

Τ_σ = mα . Η τιμή της στατικής τριβής, την οποία ασκεί το κάλυμμα στο πιάτο, έχει όμως κάποιο όριο, είναι αδύνατον να ξεπεράσει το γινόμενο «μ_σΝ, συντελεστής στατικής τριβής επί κάθετη δύναμη». Άρα αν το τράβηγμα γίνει απότομα, με επιτάχυνση δηλαδή μεγαλύτερη από κάποια τιμή, η στατική τριβή δεν μπορεί να συμπαρασύρει το πιάτο. Αν θέλουμε να προσδιορίσουμε τη μέγιστη τιμή επιτάχυνσης μπορούμε να βασιστούμε στις σχέσεις Τ_σ,max = mα και Ν = mg που απορρέεουν από τον δεύτερο νόμο και στη σχέση

Τ_σ,max = μ_σΝ η οποία περιγράφει τη μέγιστη τιμή στατικής τριβής. α _max = μ_σg .

8. Μήπως πονάει και δεν το δείχνει ;

Ο καθηγητής της φυσικής έχει την παλάμη του οριζόντια πάνω στο θρανίο κι έχει βάλει πάνω έναν αλτήρα με το κάτω πεπλατυσμένο άκρο του να στηρίζεται στην παλάμη του . Ο μαθητής κρατάει ένα βαρύ σφυρί,

το σηκώνει και κτυπά τον αλτήρα στο πάνω πεπλατυσμένο άκρο.

Ο καθηγητής δεν δείχνει να ενοχλείται. Τι συμβαίνει ; Μήπως πονάει και δεν το δείχνει ;

8. Ένας ιδιαίτερος ρόλος για τη μάζα/αδράνεια : . Ας φανταστούμε δύο σώματα το Α και το Β σε επαφή και στο ένα από αυτά- το οποίο έχει ορισμένη μάζα – ασκηθεί εξωτερική δύναμη F , η δύναμη που θα ασκήσει το Α στο Β – εφόσον στο σύστημα εκδηλώνεται επιτάχυνση, θα είναι μικροτερη από την F. Η τιμή της μάζας του σώματος Α θα καθορίσει τη μείωση της δύναμης . Με άλλα λόγια η ασκούμενη στο ένα σώμα δύναμη δεν διαβιβάζεται αναλλοίωτη εφόσον το σώμα έχει μάζα. Αμελητέα μείωση θα έχουμε μόνο στην περίπτωση που η μάζα του Α είναι αμελητέα, όπως στην περίπτωση μιας δύναμης F που ασκείται στο άκρο νήματος με αμελητέα μάζα, oπότε θεωρούμε ότι η δύναμη που εκδηλώνεται στο άλλο άκρο είναι περίπου ίση με τη F. Αντίθετα εάν η μάζα του παρεμβαλλόμενου σώματος είναι σημαντική σε σχέση με τις μάζες των υπόλοιπων σωμάτων , η μείωση μπορεί να είναι σημαντική.

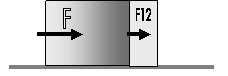Πρόκειται για ένα είδος ιδιοτητας της μάζας/αδράνειας η οποία περιγράφεται από τον δεύτερο νόμο της κίνησης. Ας χρησιμοποιήσουμε ένα παράδειγμα μοντέλο με οριζόντιο έδαφος χωρίς τριβή.

Αν τον εφαρμόσουμε τον δεύτερο νόμο στο σώμα Α F – F₁₂ = m₁α .

Αν τον εφαρμοσουμε στο σύστημα F = (m₁ + m₂)α .

Προκύπτει ότι η ΔΙΑΦΟΡΑ F – F₁₂ καθορίζεται και από τη μάζα του παρεμβαλλομενου σώματος και μόνο εάν η επιτάχυνση είναι μηδενική η διαφορά μηδενίζεται. Προκύπτει επίσης ότι ο ΛΟΓΟΣ F₁₂ /F είναι ίσος με m₁ /(m₁ + m₂) ή ίσος με 1/ ( 1+λ) όπου λ ο λόγος των μαζών. Θα μπορούσαμε – κάπως ελεύθερα και χωρίς επιστημολογικά νόμιμη διατύπωση – να πούμε ότι « η μάζα δεν επιτρέπει την αναλλοίωτη μεταφορά μιας δύναμης» .

Στην περίπτωση του σφυριού η δύναμη που ασκείται στο χέρι του καθηγητή είναι μικρότερη από εκείνη που ασκείται με το σφυρί στην άλλη άκρη του αλτήρα. Αν η μάζα του αλτήρα είναι γύρω στα δύο kg , η μείωση είναι τόσο πιο μικρή ώστε σε συνδυασμό με τη σχετικά μεγάλη επιφάνεια του αλτήρα η αύξηση της πίεσης που εκδηλώνεται στο χέρι του καθηγητή να του επιτρέπει να μην πονάει .

9. Αν φυσήξουμε ανάμεσά τους ;

Δυο φύλλα από χαρτί. Κρατάμε το ένα με το δεξί χέρι, από το πάνω μέρος ελαφρά , ώστε να διατηρείται κατακόρυφο, το άλλο με το αριστερό με τον ίδιο τρόπο , τα δύο φύλλα είναι παράλληλα και κατακόρυφα και σχετικά κοντά το ένα με το άλλο. Φυσάμε ανάμεσά τους. Τι προβλέπουμε ότι θα συμβεί;

9. Τα δύο φύλλα θα πλησιάσουν. Ένας μαθητής του ελληνικού σχολείου δεν θα μπορέσει να κάνει μια πρόβλεψη σε αυτό που θα συμβεί ή να δώσει μια εξήγηση σε αυτό που είδε. Κι αυτό διότι ούτε και στο Λύκειο διδάσκεται τον τόσο σημαντικό στην εξέλιξη της Φυσικής νόμο του Bernoulli . Το 1738 ο Daniel Bernulli, γεννημένος στην Ολλανδία από γονείς ελβετικής καταγωγής, δημοσίευσε το Hydrodynamica στο οποίο παρουσίασε τον περίφημο νόμο για τη στρωτή ροή των ρευστών.

Σε μια πιο σύγχρονη διατύπωση : Σε κάθε στρωτή ροή, κατά μήκος μιας ρευματικής γραμμής, το άθροισμα της κινητικής ενέργειας ανά μονάδα όγκου του ρευστού και της πίεσης διατηρείται σταθερό. ½ρυ² + p = σταθερό . Η ανά μονάδα όγκου κινητική ενέργεια λέγεται δυναμική πίεση. Αν εφαρμόσουμε τον νόμο σε ροή που μπορεί προσεγιστικά να θεωρηθεί στρωτή, καταλήγουμε σε συμπεράσματα του τύπου

« αύξηση της ταχύτητας ροής συνεπάγεται μείωση της υφιστάμενης πίεσης»

10. Το κουταλάκι του γλυκού και το νερό της βρύσης .

Κρατάει στο χέρι το κουταλάκι του γλυκού και με το άλλο ανοίγει τη βρύση και τρέχει το νερό. Προσέχει ότι η φλέβα της ροής προς τα κάτω γίνεται όλο και πιο λεπτή. Αναρωτιέται «γιατί ;» . Πλησιάζει το κουταλάκι με την κυρτή του πλευρά προς τη φλέβα. Προβλέπει ότι η φλέβα του νερού θα σπρώξει το κουταλάκι, η δύναμη του νερού θα το απωθήσει, όπως συμβαίνει με την αστυνομία και τους φοιτητές στα συλλαλητήρια. Βλέπει όμως αλλά και «νιώθει» ότι το κουταλάκι προσκολλάται στο νερό λες και διψάει. Θα ρωτήσει τον φυσικό στο σχολείο.

10. Η στρωτή ροή ιδανικού ρευστού υπακούει και στον στον νόμο Bernoulli αλλά και στον νόμο της συνέχειας ή νόμο της σταθερής παροχής, σύμφωνα με τον οποίο «η παροχή διατηρείται σταθερή» . Αλλά η παροχή -όγκος ρευστού ανά μονάδα χρόνου – είναι ίση με το γινόμενο « ταχύτητα ροής επί εμβαδόν διατομής της φλέβας». Ο νόμος συνεπώς διατυπώνεται και με τη σχέση s. υ = σταθερό.

Καθώς τρέχει το νερό της βρύσης, η ταχύτητα ροής αυξάνεται . Οι «προς τα κάτω» ποσότητες νερού έχουν μεγαλύτερες ταχύτητες από εκείνες των « πιο πάνω». Αν δεχθούμε προσεγγιστικά τη ροή στρωτή, οι μεγαλύτερες τιμές ταχύτητας - σύμφωνα με τον νόμο s.υ = σταθερό, αντιστοιχούν σε μικρότερο εμβαδόν διατομής της φλέβας.

Αν τώρα εφαρμόσουμε τον νόμο του Bernoulli καταλήγουμε στο συμπέρασμα ότι οι μεγαλύτερες ταχύτητες συνεπάγονται μικρότερες τιμές πίεσης. Σε σημεία κοντά στη φλέβα εκδηλώνεται καποια υποπίεση – σε σχέση με την ατμοσφαιρική και το κουταλάκι από τη μια πλευρά, την κυρτή, δέχεται πιεστικές δυνάμεις από τον αέρα που σπρώχνει – πίεση ατμοσφαιρική – ενώ από την άλλη πλευρά,

προς το μέρος της φλέβας, οι αντίστοιχες δυνάμεις είναι μικρότερες με συνέπεια να προσκολλάται στο νερό, λες και διψάει.

11. Η σούπα, η ανάμνηση μιας ψύξης και η μαμά με το οινόπνευμα.

Το κουτάλι της σούπας, γεμάτο με σούπα, είναι κοντά στο στόμα του κι εκείνος τη φυσάει γιατί είναι πολύ ζεστή . του όταν είναι ζεστή; Φυσώντας την νομίζει ότι η σούπα κρυώνει . Έχει δίκιο ; Θυμάται, τότε πολύ μικρός, είχε γδάρει άσχημα το χέρι του, και η τότε μαμά είχε βάλει οινόπνευμα με βαμβάκι και το φύσαγε. Γιατί το φύσαγε ; Ήθελε να το κρυώσει ;

11. Πρόκεται για το φαινόμενο εξάτμιση. Όπως και στον βρασμό, όταν συμβαίνει εξάτμιση το υγρό αποσπά θερμική ενέργεια από οπουδηποτε, ακομα και από τον εαυτό του.

Η ταχύτητα της εξάτμισης – μάζα εξατμιζόμενου υγρού ανά δευτερόλεπτο – εξαρτάται από τη μερική πίεση των ατμών

του ίδιου υγρού ( αν είναι νερό θα είναι οι υδρατμοί ) αλλά και από την ολική πίεση στην ελεύθερη επιφάνεια του υγρού.

Καθώς εκείνος φυσάει τη σούπα , δημιουργεί κυρίως – όχι μόνο – μεγάλη ταχύτητα στις ποσότητες αέρα που βρίσκονται στην επιφάνεια με συνέπεια – σύμφωνα με τον νόμο του Bernoulli – να διαμορφώνεται μειωμένη πίεση και να αυξάνεται η ταχύτητα εξάτμισης . Αλλά το υγρό για να υγρό για να ατμοποιηθεί , και εφόσον οι συνθήκες υπάρχουν η ατμοποίησή του θα λάβει χώρα και μάλιστα με μεγαλύτερη ταχύτητα , θα αποσπάσει θερμική ενέργεια από τον εαυτό του και η θερμοκρασία του θα ελαττωθεί .

Στην αύξηση της ταχύτητας εξάτμισης συνέβαλε , αλλά σε μικρότερο βαθμό, και η απομάκρυνση υδρατμών από την επιφάνεια της σούπας

Με παρόμοιο τρόπο εξηγείται γιατί τότε που είχε λουστεί και βγήκε με βρεγμένα τα μαλλιά, βόλτα με το μηχανάκι, έπαθε ψύξη. Οι προυποθέσεις για ταχύτατη εξάτμιση υπήρχαν – η κίνησή του με το μηχανάκι σήμαινε και μεγάλη ταχύτητα ροής του αέρα, άρα σοβαρή μειωση της πίεσης - και το νερο για να εξατμιστεί αποσπούσε με μεγάλους ρυθμούς θερμική ενέργεια από το κεφάλι του.

Τότε που φύσαξε η μαμά το οινόπνευμα προκαλούσε αύξηση της ταχύτητας εξάτμισης και η εξάτμιση η οποία στην περίπτωση του οινοπνεύματος ούτως ή άλλως θα προχωρούσε με γρήγορο ρυθμό, επιταχύνθηκε ακόμα περισσότερο

12. Αναμνήσεις με φυσήματα ΙΙ . Η τούρτα με τα κεριά

Θυμάται τότε, στα γενέθλια των δώδεκα που έπρεπε να σβήσει τα κεριά , κι εκείνος φύσηξε όσο μπορούσε πιο δυνατά, αλλά τα περισσότερα έμειναν αναμμένα. Τι συμβαίνει και όταν φυσάμε σβήνει το κερί ;

12. Όταν φυσήξουμε για να σβήσει το κερί εκδηλώνονται δύο τουλάχιστον συνέπειες . Η μία είναι ότι απομακρύνονται θερμοί ατμοί παραφίνης και άλλη είναι η υποπίεση . Και οι δύο συνεργάζονται στο να μη μπορεί να διατηρηθεί η καύση. Σχετικά με την υποπίεση, σύμφωνα με τον νόμο Bernoulli, η σχετικά μεγάλη ταχύτητα συνεπάγεται σχετικά μικρή πίεση. Εκεί που φυσάμε, η μειωμένη πίεση σημαίνει και μειωμένη πυκνότητα αέρα άρα και μειωμένη παρουσία του οξυγόνου, του αναγκαίου για τη διατήρηση της καύσης.

13. Τελικά λέρωσε το τραπεζομάντηλο.

Το ποτήρι ήταν σχεδόν γεμάτο με κρασί. Το σήκωσε και δοκίμασε να το γύρει ώστε να χύσει λίγο στο διπλανό άδειο ποτήρι. Το έγειρε λίγες μοιρες κάνοντας την κίνηση αργά και προσεκτικά . Είδε ότι αντί το κρασί να χύθεί με μια κατακόρυφη φλέβα , μόλις πέρασε το χείλος του ποτηριού προσκολλήθηκε στο ποτήρι και δημιουργήθηκε μια φλέβα η οποία τελικά λέρωσε το τραπεζομάντηλο. Η αγαπημένη του τον κοίταξε επιτιμητικά κι εκείνος ένιωσε αμήχανα. Έχει σκοπό να ρωτήσει τους φυσικούς γιατί συμβαίνει αυτό ;

13. Επειδή έκανε την κίνηση αργά, άφησε δηλαδή το κρασί να χύνεται λίγο λίγο, η λεπτή φλέβα - λόγω του νομου της συνέχειας - που δημιουργήθηκε έχει λόγω μικρού εμβαδού - βάσει του νομου της συνέχειας, s.υ = σταθερό - σχετικά μεγάλη αρχική ταχύτητα. Αυτό έχει ως συνέπεια – βάσει του νόμου Benmoulli – να εκδηλώνεται σχετικά μικρή πίεση, μικρότερη από την ατμοσφαιρική. Η επόμενη συνέπεια είναι ότι ο ατμοσφαιρικός αέρας σπρώχνει τη λεπτή φλέβα προς το ποτήρι, χωρίς «σοβαρές αντιρρήσεις» και η φλέβα να προσκολλάται στην εξωετρική επιφάνεια του ποτηριού και να ρέει προς τα κάτω προσκολλημένη εκεί.

14. Ψηλός, ψηλός καλόγερος

Έβλεπε το αναμένο τσιγάρο της μαμάς στο τασάκι και ρώτησε γιατί ο καπνός αφού ανέβει λίγο δημιουργεί δίνες ; Η μαμά θυμήθηκε, τότε που ήταν μικρή, το αίνιγμα «ψηλός, ψηλός καλόγερος και κόκκαλα δεν έχει» αλλά το μόνο που της είπε ήταν « που θες να ξέρω;»

14. Αν η ταχύτητα ενός ρευστού σε στρωτή ροή υπερβεί την τιμή της λεγόμενης κρίσιμης ταχύτητας , η στρωτή ροή γίνεται τυρβώδης.

Τα θερμά αέρια από το αναμμένο τσιγάρο έχουν αρχικά σχεδόν στρωτή ροή εξαιτίας της σχετικά αργής ανοδικής κίνησης . Ωστόσο, κατά την άνοδό τους, η άνωση που ασκείται από τον σχετικά πιο ψυχρό αέρα του περιβάλλοντος προκαλεί αύξηση της ταχύτητάς τους με αποτέλεσμα, ύστερα από δύο περίπου cm ανόδου, η ροή να αρχίσει να μετατρέπεται σε τυρβώδη .

15. Λες και η βαρύτητα ξεχάστηκε

Το έκανε μόνη της στο σπίτι. Το νερό στο ποτήρι, από πανω ένα φύλλο από χαρτί, αναστρέφει το ποτήρι και το νερό δεν χύνεται, το χαρτί μένει κολλημένο στα χείλη του ποτηριού και δεν πέφτει, λες και η βαρύτητα ξεχάστηκε.

15. Όταν βάζει προσεκτικά το χαρτί πάνω στο ποτήρι, το κλείσει αεροστεγώς όσο γίνεται και το αναστρέφει , το νερό μετακινείται

προς τα κάτω και ανάμεσα στον πυθμένα του ανεστραμμένου ποτηριού ο οποίος τώρα βρίσκεται από πάνω και στην επιφάνεια του νερού υπάρχει πολύ λίγος αέρας με αντίστοιχα πολύ μικρή πίεση . Οι δυνάμεις που ασκούνται στη στήλη του νερού είναι το βόρος της, η πιεστική δύναμη από πάνω προς τα κάτω από τον εγκλωβισμένο ελάχιστο αέρα και η πιεστικη δύναμη προς τα πάνω από τον εξωτερικό αέρα η οποία μπορεί και ισορροπεί τις άλλες δύο .

16. Ποιος είναι ο δρόμος του φωτός ;

Ένα σημείο Α στον αέρα, ένα σημείο Β στο νερό και η επίπεδη επιφάνεια που τα διαχωρίζει. Το φως για να ταξιδέψει από το Α στο Β ακολουθεί τον δρόμο τον χωρικά πιο σύντομο, τον δρόμο τον χρονικά πιο σύντομο ή τον δρόμο για τον οποίο ημθ_α/ημθ_β = c_α/c_β όπου θ_α και θ_β οι είναι οι γωνίες πρόσπτωσης και διάθλασης στη διαθλαστική επιφάνεια και c_α, c_β οι τιμές της ταχύτητας του φωτός σε αέρα και νερό αντίστοιχα.

16. Το 1621 ο μαθηματικός Willebrord Snell προτείνει μία διατύπωση του νόμου της διάθλασης. Ο νόμος των ημιτονων, τον οποίο αποδεχόμαστε και σήμερα, διακηρύσσει ότι κατά τη διάθλαση ο λόγος ημθ_α/ημθ_β έχει τιμή σταθερή , δηλαδή ανεξάρτητη από την τιμή της γωνίας πρόσπτωσης. Βέβαια το ερώτημα «γιατί ο λόγος ημα/ημβ είναι σταθερός;» ή «ποια γενικότερη θεώρηση για τη συμπεριφορά του φωτός καθόριζε από τη σταθερότητα του συγκεκριμένου λόγου;» έμεινε αναπάντητο.

Το 1637 ο Descartes – Καρτέσιος - παρουσίασε τον νόμο σε γραπτό κείμενο αλλά έδωσε και μια απάντηση στο «γιατί ο λόγος των ημιτόνων είναι σταθερός». Η απάντηση ήταν ότι «ο λόγος αυτός είναι σταθερός διότι το φως έχει ΣΩΜΑΤΙΔΙΑΚΗ υπόσταση και τα σωματίδια υπακούουν στη διατήρηση της ορμής. Ο ίδιος απέδειξε ότι ο λόγος αυτός είναι ίσος με τον λόγο των ταχυτήτων του φωτός και συγεκριμένα ημα/ημβ = c_β/c_α αλλά για να ερμηνεύση το εμπειρικό δεδομένο της σχετικα μικρότερης γωνίας διάθλασης ( α > β ) ήταν υποχρεωμένος να αποδεχθεί ότι η ταχύτητα c_α του φωτός στον αέρα ήταν μικρότερη από την αντίστοιχη c_β στο γυαλί.

To 1645 o Pierre Fermat, προτείνοντας τη σχετική Αρχή, χωρίς να ασχοληθεί με το φύση του φωτός απέδειξε ότι ο χρονικά πιο σύντομος δρόμος του φωτός κατά τη διάθλαση είναι εκείνος για τον οποίο ημα/ημβ = c_α/c_β . Απέδειξε δηλαδή ότι ο λόγος των ημιτόνων είναι το αντίστροφο το λόγου των ταχυτήτων στον οποίο είχε καταλήξει ο Καρτέσιος και ταυτόχρονα έδειξε ότι η σταθερότητα του λόγου δεν οφείλεται στη σωματιδιακότητα του φωτός αλλά στο ότι ακολουθεί τον χρονικά πιο σύντομο δρόμο

Το 1678 ο επίσης Ολλανδός Christian Huygens απέδειξε με Γεωμετρία ότι και ο Fermat, ότι ισχύει δηλαδή ημα/ημβ = c_α/c_β αποδεχόμενος ΚΥΜΑΤΙΚΗ υπόσταση για το φως και προτείνοντας μία Αρχή για τη διάδοση οποιουδήποτε κύματος .

Τον 19^ο αιώνα ο Foucault μέτρησε την ταχύτητα του φωτός σε γυαλί και αποσαφηνίστηκε ότι είναι μικρότερη από την αντίστοιχη στον αέρα . Αυτό σήμαινε ότι ο Fermat και ο Huygens είχαν δίκιο και όχι ο Καρτέσιος

Λίγο αργότερα ο Maxwell παρουσίασε την Ηλεκτρομαγνητική θεωρία και φάνηκε ότι ο νόμος της διάθλασης απορρέει από αυτήν , ενώ οι φυσικοί του 20^ου αιώνα έδειξαν ότι ο νόμος είναι συνέπεια των Αρχών της Κβαντομηχανικής

Η απάντηση λοιπόν στο ερώτημα είναι ότι ο δρόμος του φωτός είναι ο δρόμος για τον οποίο ημθ_α/ημθ_β = c_α/c_β ο οποίος είναι ΚΑΙ ο χρονικά πιο σύντομος από όλους τους άλλους που θα μπορούσαν να συνεδέσουν το σημείο Α με το σημείο Β.