Ανδρέας Ιωάννου Κασσέτας

Οι ΑΠΑΝΤΗΣΕΙΣ στα ερωτήματα 17 έως 32 .

17. Το κερί έσβησε και το νερό ανέβηκε .

Το είδε με τα μάτια της . Έβαλε ένα αναμμένο κερί σε μικρή λεκάνη με λίγο νερό, κι ύστερα με ένα ποτήρι ανεστραμμένο σκέπασε το αναμμένο κερί . Ειδε το κερί να σβήνει και το νερό να ανεβαίνει. Τι λένε γι αυτό οι φυσικοί ;

17. Δεν είναι μόνο οι φυσικοί που πρέπει να πουν κάτι. Χρειάζονται και οι χημικοί . Όταν είναι αναμμένο το κερί, ατμοποιούνται οι υδρογονάνθρακες -παραφίνη -, οι θερμοί ατμοί αντιδρούν χημικά με το ΟΞΥΓΟΝΟ και οι χημικοί μιλούν για καύση. Τα θερμά αέρια ανυψώνονται . Τελικά το ατμοποιημένο κερί δημιουργεί διάφορα προϊόντα σχηματίζοντας και σωματίδια αιθάλης . Γι αυτό και στην πάνω πλευρά του ανεστραμμένου ποηριού μπορεί να δημιουργηθεί καπνιά. Η καύση έχει ως αποτέλεσμα να ελαττωθεί

το οξυγόνο, σε βαθμό που σε λίγο δεν επαρκεί για τη διατήρηση της αναμμένης φλόγας.

Το χρονικό διάστημα που το κερί διατηρείται αναμμένο εξαρτάται από τον όγκο του ποτηριού. Οι μετρήσεις δείχνουν ότι διατηρείται για 7 περίπου δευτερόλεπτα αναμμένο αν το ποτήρι είναι 300 ml ( όγκος εγκωβισμένου αέρα 220 ml περίπου ) , 12 s περίπου αν το ποτήρι είναι 400 ml (όγκος αέρα 320 ml περίπου) και γύρω στα 27 s αν το γυάλινο δοχείο είναι 1000 ml και ο όγκος αέρα περίπου 910 ml.

Σε αυτό το χρονικό διάστημα εκδηλώνονται δύο αντιτιθέμενες συνέπειες αυτού που συμβαίνει .

Η μία είναι η, λόγω της καύσης, ελάττωση του οξυγόνου η οποία θα συνέβαλε στην ελάττωση της πίεσης του εγκλωβισμένου αέρα.

Η άλλη συνέπεια είναι η ταυτόχρονη αύξηση της θερμοκρασίας του αέρα και η εμφάνιση διοξειδίου του άνθρακα και υδρατμών η οποία θα συνέβαλε στην αύξηση της πίεσης. Οι δύο, αντιστρατευόμενη η μία άλλη, συνέπειες, έχουν ως αποτέλεσμα να διατηρείται η πίεση περίπου – σε επίπεδο παρατήρησης – σταθερή .

Όταν όμως σβήσει το κερί το αποτέλεσμα «αύξηση της θερμοκρασίας» συρρικνώνεται ενώ λαμβάνει χώρα και υγροποίηση των υδρατμών για να επικρατήσει το αποτέλεσμα «μείωση της μάζας του αέρα». Αν κάνουμε τον χημικό «απολογισμό» διαπιστώνεται ότι μια ποσοτητα οξυγόνου από το προϋπάρχον στον αέρα και μια ποσότητα ατμών παραφίνης δεν υπάρχει πια και με την καύση «εμφανίστηκε» διοξείδιο του άνθρακα και υδρατμοί. Οι υδρατμοί όμως υγροποιούνται και δεν συμμετέχουν στη διαμόρφωση της πίεσης του εγκλωβισμένου αέρα ενώ η χημική αντίδραση μιας πλήρους καύσης κορεσμένου υδρογονάνθρακα δείχνει καθαρά ότι η μάζα, σε moles , οξυγόνου που «χάνεται» είναι μεγαλύτερη από τη μάζα, σε moles , του διοξειδίου του άνθρακα που δημιουργείται . Εκτός από αυτά δημιουργούνται και σωματίδια αιθάλης που δεν συμμετέχουν στη διαμόρφωση της τελικής πίεσης . Η πίεση διαμορφώνεται τελικά μικρότερη από την προηγούμενη – που ήταν ίση με την ατμοσφαιρική- με συνέπεια να εισέρχεται νερό και η στάθμη στο εσωτερικό του ανεστραμμένου ποτηριού να ανεβαίνει μέχρι να εξισορροπηθεί η διαφορά των πιέσεων.

18. Το χρυσόψαρο και η γατούλα σκέτο θηλυκό

Η γάτα κοιτάζει από πάνω το χρυσόψαρο και το βλέπει πιο κοντά της από όσο στην πραγματικότητα βρίσκεται. Το χρυσόψαρο κοιτάζει προς τα πάνω τη γάτα και τη βλέπει πιο μακριά, πιο ψηλά, από τη θέση που εκεινη βρίσκεται. Τι λένε οι φυσικοί ;

18. Ένα σημείο Α του χρυσόψαρου εκπέμπει φως κι εμείς σχεδιάζουμε μία λεπτή φωτεινή δέσμη αποκλίνουσα με στίγμα το σημείο Α.

Στην επιφάνεια του νερού το φως διαθλάται, έτσι ώστε κάθε φωτεινή ακτίνα να «απομακρύνεται» από την κάθετο. Η μετά τη διάθλαση λεπτή φωτεινή δέσμη φαίνεται να προέρχεται από ένα σημείο Α΄το οποίο βρίσκεται πιο ψηλά από το Α. Βέβαια μόνο για μικρές γωνίες ( ημθ = εφθ ) η διαθλασμένη δέσμη διατηρείται στιγματική . Αυτό σημαίνει ότι μόνο εφόσον ο παρατηρητής βρίσκεται στην κατακόρυφο του Α βλεπει το είδωλο από διάθλαση σαφές. Αν είναι n ( n = 4/3) o δείκτης διάθλασης του νερού ως προς τον αέρα, h₁ και h₂ οι αποστάσεις των Α και Α΄ από τη διαθλαστική επιφάνεια, d η απόσταση του σημείου πρόσπτωσης μιας φωτεινής ακτίνας από την προβολή του Α στη διαθλαστική επιφάνεια και θ₁ , θ₂ οι γωνίες πρόσπτωσης και διάθλασης, ισχύει d = h₁εφθ₁ και d = h₂εφθ₂ άρα h₁εφθ₁ = h₂εφθ₂ Σύμφωνα με τον νόμο της διάθλασης ισχύει επίσης nημθ₁ = ημθ₂ . Εφόσον οι γωνίες ειναι μικρές ημθ₁ = εφθ₁ και ημθ₂ = εφθ₂ , οπότε h₂ = h₁/n . Αν το σημείο Α του χρυσόψαρου βρίσκεται 28 εκατοστά κάτω από την επιφάνεια του νερού, η γάτα το αντιλαμβάνεται στα 21 εκατοστά

Ένα σημείο Β της γάτας, σε ύψος Η₁ από την επιφάνεια του νερού εκπέμπει φως . Με αντίστοιχο συνδυασμό Φυσικής και Γεωμετρίας καταλήγουμε στο συμπέρασμα ότι η λεπτή δέσμη που εισέρχεται στο νερό φαίνεται να προέρχεται από ένα σημείο Β΄ πιο ψηλά από τα Β, σε ύψος Η₂ , για το οποίο Η₂ = nH₁ . Εάν υποθέσουμε οτι η λειτουργία της όρασης του χρυσόψαρου είναι παρόμοια με τη δική μας -πράγμα για το οποίο δεν είμαστε καθόλου βέβαιοι – το χρυσόψαρο βλέπει τη γάτα πιο ψηλά απο τη θέση στην οποία εκείνη βρίσκεται.

19. Ποια είναι η τροχιά του άκρου της σκιάς ;

Ιούλιος, στα Πολώνια της Μήλου, ώρα δέκα το πρωί. Ένα ίσιο ραβδί, περίπου ένός μέτρου, στερεωμένο στην άμμο κατακόρυφα κι εκείνος να βάζει κάθε τόσο ένα μικρό λευκό βοτσαλάκι «εκεί που τελειώνει η σκιά». Ύστερα από μερικές ώρες στην παραλία, διαπιστώνει ότι το μικρότερο μήκος σκιάς εμφανίζεται κατά το μεσημέρι αλλά αυτό το είχε προβλέψει. Διαπιστώνει όμως ότι στις ώρες που πέρασαν το άκρο της σκιάς διαγράφει μια τροχιά που θυμίζει το μισό μιας έλλειψης. Σκέφεται να αποδείξει με συλλογισμούς ότι πράγματι το άκρο της σκιάς διαγράφει έλλειψη.

Η παρατήρηση . Τις πρωινές ώρες η σκιά του ραβδιού είναι αρκετά μεγάλη, στη συνέχεια μικραίνει, το μήκος της αποκτά τη μικρότερη τιμή του κατά το μεσημέρι και στη συνέχεια μεγαλώνει , για να φθάσει το απόγευμα σε μεγάλες τιμές και γύρω στις επτά η σκιά χάνεται για το βλέμμα μας παρόλο που το φως ακόμα υπάρχει. Φαίνεται ότι δεν επαρκεί για να εμφανιστεί σκιά ευδιάκριτη. Είναι η «ώρα που σβήνουν οι σκιές», όπως λένε οι ποιητές.

Η σκέψη . Σε κάποια χρονική στιγμή, εκείνος εντοπίζει το 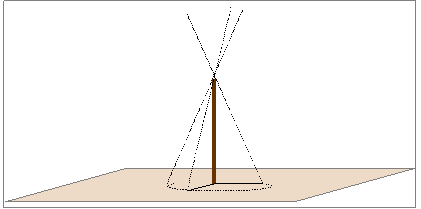άκρο της σκιάς και το θεωρεί γεωμετρικό σημείο. Ενώνει με τη φαντασία του το σημείο αυτό με την κορυφή του ραβδιού Ο.

Δημιουργείται μια ημιευθεία , η προέκταση της οποίας προς τον ουρανό σημαδεύει τον ήλιο.

Το επαναλαμβάνει μία άλλη χρονική στιγμή και δημιουργείται μία άλλη ημιευθεία.

Το σύνολο των ημιευθειών συνιστά επιφάνεια κώνου.

Ο κώνος αυτός με κορυφή το σημείο Ο , τέμνεται από το έδαφος και η τομή - κωνική τομή-

θα είναι μία έλλειψη ή,

για την ακρίβεια, τμήμα μιας έλλειψης.

20. Χειμώνες και καλοκαίρια

Γιατί κάνει κρύο το χειμώνα και το καλοκαίρι ζέστη. Έχει μια θεωρία που το εξηγεί ότι «το καλοκαίρι ο ήλιος είναι πιο κοντά στη Γη» αλλά την κρατάει για τον εαυτό του. Τις προάλλες σκέφτηκε πως όταν στην Ελλάδα έχει καλοκαίρι στην Αυσταλία έχει χειμώνα και κατάλαβε ότι η θεωρία του δεν στέκει. Γιατί τελικά υπάρχουν οι εποχές;

20. Στον πλανήτη Γη που μεγαλώσαμε οι εποχές εναλλάσσονται λόγω του ότι η Γη περιφέρεται γύρω από τον Ήλιο 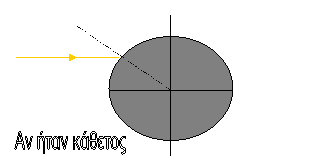με έναν συγκεκριμένο τρόπο.Ο άξονας περιστροφής της ημερήσιας περιστροφής της Γης δεν είναι κάθετος στο επίπεδο της τροχιάς γύρω από τον Ήλιο, αλλά σχηματίζει μια γωνία περίπου 23 μοιρών με την κάθετο στο επιπεδο αυτό. Η κάθε εποχή, σε έναν τόπο, προσδιορίζεται με τη γωνία πρόσπτωσης των ηλιακών ακτίνων στο έδαφος , το μεσημέρι, τη στιγμή της ελάχιστης σκιάς . Πρόκειται για τη γωνία που σχηματίζουν οι ακτίνες με την κατακόρυφο.

Αν ο άξονας περιστροφής ήταν κάθετος στο επίπεδο της τροχιάς,

η γωνία αυτή, για τον δικό μας λόγου χάρη γεωγραφικό πλάτος των 40 περίπου μοιρών , η γωνία πρόσπτωσης θα ήταν ίση με τη γωνία των 40 μοιρών , σε όλη τη διάρκεια του έτους αναλλοίωτη και δεν θα υπήρχαν εποχές.

21. Οι ακτίνες του ήλιου στο πηγάδι

Σε κάποια στιγμή της μέρας η σκιά ενός ραβδιού γίνεται ελάχιστη . Υπάρχει καποιο σημείο πάνω στη Γη όπου το μεσημέρι δεν δημιουργείται καθόλου σκιά ; Σε αυτήν την περίπτωση το φως του ήλιου θα έφθανε στον πυθμένα κάθε πηγαδιού

21.. Στον δικό μας πλανήτη, ο άξονας περιστροφής σχηματίζει μια γωνία περίπου 23 μοιρών με την κάθετο στο επιπεδο της τροχιάς .

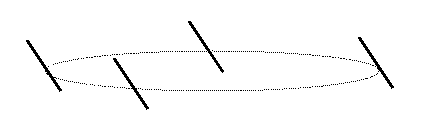
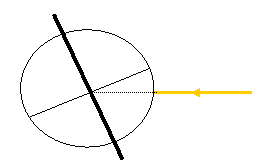Το να φθάσουν φωτεινές ακτίνες κάθετα στο έδαφος σημαίνει η προεκτασή τους να οδηγεί στο κεντρο της Γης Αυτό, λογου χάρη, συμβαίνει το μεσημέρι του θερινού ηλιοστάσιου σε περιοχές στον Τροπικο του καρκίνου που το γεωγραφικό πλάτος είναι βόρειο 23 μοιρών.

Συμβαίνει επίσης κατά το μεσημέρι του χειμερινού ηλιοστάσιου στις περιοχές που βρίσκονται στον Τροπικό του Αιγόκερω.

Το ζήτημα ωστόσο είναι αρκετά πιο σύνθετο. Μπορεί να συμβεί στο μεσημέρι μιας συγκεκριμένης ημέρας σε κάθε τόπο που περιλαμβάνεται μεταξύ των δύο τροπικών.

22. Τ΄ αστέρι του βορριά και το παιδί από τη Θεσσαλονίκη

Παρατηρώντας τον νυχτερινό ουρανό , είχε προσέξει ότι το άστρο που σου δείχνει το «που είναι ο βορράς», τ’ αστέρι του βοριά, βρίσκεται χειμώνα καλοκαίρι, στο ίδιο ύψος πάνω από τον ορίζοντα. Μια νύχτα έκανε τον υπολογισμό ότι η γωνία που της ευθείας που τον ενώνει με το άστρο με τον ορίζοντα είναι πάντα μια γωνία 40 μοιρών . Αναρωτήθηκε γιατί, αφού στο μεταξύ έμαθε ότι το άστρο για πολλούς ευρωπαίους λέγεται polaris , ενώ στη δική του γλώσσα λέγεται πολικός αστέρας.

22. Η Γη στρέφεται περί έναν άξονα ο οποιος συνδέει τον βόρειο και τον νότιο πόλο. Στην προέκταση του άξονα περιστροφής της Γης προς το μέρος του βορρά υπάρχει ένα συγκεκριμένο 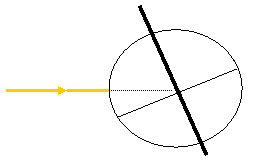άστρο, ο πολικός αστέρας. Επειδή είναι αυτή η θέση του κατά την ημερήσια περιστροφή της Γης δεν αλλάζει θέση, δεν ανατέλλει, ούτε και δύει όπως τα άλλα άστρα κι αυτό διότι η ευθεία- άξονας περιστροφής του πλανήτη μας, παραμένει πάντα ίδια. Το ίδιο συμβαίνει και κατά την ετήσια περιφορά γύρω από τον Ήλιο διότι κατά την κίνηση αυτή ο άξονας περιστροφής δεν αλλάζει κατύθυνση, από την πλευρά του βορρά «κοιτάζει» πάντα προς τον πολικό αστέρα. Με βάση τη Γεωμετρία αποδεικνύεται εύκολα ότι η γωνία που σχηματίζει η εφαπτομένη σε ένα τόπο ( ο ορίζοντας ) με την ευθεία που συνδέει τον τόπο με τον πολικό αστέρα, είναι ίση με τη γωνία που σχηματίζει η κατακόρυφος του τόπου με το επίπεδο του Ισημερινού. Η δεύτερη αυτή γωνία είναι το ΓΕΩΓΡΑΦΙΚΟ ΠΛΑΤΟΣ και βέβαια βόρειο διότι οι κατοικοι του νότιου ημισφαιρίου, όπως είναι τα παιδιά στην Νέα Ζηλανδία και στην Αγγόλα δεν βλεπουν polaris. Άρα η γωνία στην οποία φαίνεται ο πολικός αστέρας πάνω από τον ορίζοντα του τόπου είναι το βόρειο γωγραφικό πλάτος του τόπου. Κάποιος που ζει στον βόρειο πόλο βλέπει τον πολικό να βρίσκεται κάθε νύχτα στο ζενίθ, στην κατακόρυφο, να βρίσκεται με άλλα λόγια, 90 μοίρες πάνω από τον ορίζοντα , ενώ ένα παιδί που βρίσκεται στο Εκουαδόρ και τις νύχτες κοιτάζει τα άστα βλέπει τον polaris στον ορίζοντα. .

Ο δικός μας παρατηρητής που βλέπει κάθε φορά στον polaris 40 πάνω από τον ορίζοντα είναι παιδί της Θεσσαλονίκης . Το γεωγραφικό πλάτος της Θεσσαλονίκης είναι 40⁰ 37΄ . Στο ίδιο περίπου ύψος βλέπουν τον polaris οι νυχτερινοί παρατηρητές της Μαδρίτης, συνηθως οπαδοί της Ρεάλ, Ιταλοί στον νυχτερινό ουρανό της Νάπολης , Κινέζοι παρατηρητές του Πεκίνου, Τούρκοι παρατηρητές της Άγκυρας και Αμερικανοί της Νέας Υόρκης.

23. Ο σαργός και ο άνθρωπος

Ο Κώστας, αν και όχι τόσο νεαρός, συνηθίζει να κάνει καταδύσεις αναζητώντας σαργούς και μαγιάτικα και βέβαια για να βλέπει καλύτερα φορά και μάσκα. Και όχι μόνο αυτός . Γιατί βλέπουμε καλύτερα στο νερό με τη μάσκα; Ο σαργός όμως πώς βλέπει χωρίς μάσκα ;

23. Για να δημιουργηθεί σαφές είδωλο στον αμφιβληστροειδή, πρέπει το φως να υποστεί διάθλαση στον φακό του ματιού, ο δείκτης διάθλασης του οποίου διαφέρει από τον αντίστοιχο του αέρα. Ένα σημαντικό «ποσοστό» από τη φωτεινή ακτινοβολία που πέφτει στο μάτι μας διαθλάται στην «επιφάνεια» του ματιού. Εάν το νερό βρίσκεται σε επαφή με το μάτι, η διάθλαση αυτή στο μεγαλύτερο μέρος της περίπου ματαιώνεται γιατί ο δείκτης διάθλασης τουνερού είναι περίπου ίσος με τον δείκτη διάθλασης του φακού του ματιού μας

Όταν φοράμε μάσκα, το στρώμα του αέρα που παρεμβάλλεται ανάμεσα στο γυαλί και το μάτι μας εξασφαλίζει μια φυσιολογική διάθλαση και βλέπουμε όπως εάν φορούσαμε γυαλιά χωρίς φακούς . Ο σαργός βλέπει ταυτόχρονα και στο νερό και στον αέρα διότι διαθέτει δύο αμφιβληστροειδείς και έναν φακό σε σχήμα αυγού. Το τμήμα του φακού που βρίσκεται μέσα στο νερό έιναι περισσότερο καμπυλωμένο ώστε να πραγματοποιείται η διάθλαση του φωτός που προέρχεται από τον υποβρύχιο κόσμο.

24. Δορυφόρος πάνω από το Σύνταγμα

Είναι δυνατόν να εκτοθευτεί ένας δορυφόρος που να βρίσκεται συνεχώς πάνω από την πλατεία Συντάγματος ;

Πρέπει η εκτόξευση να γίνει σε ορισμένο ύψος ή μήπως είναι αδύνατον να πραγματοποιηθεί ;

24. Μια εκτόξευση από κατάλληλο ύψος μπορεί να δημιουργήσει περιφορά με περίοδο 24 ωρών, ίση με την περίοδο περιστροφής της Γης.. Για να διατηρείται όμως στάσιμος πρέπει να έχει την ίδια γωνιακή ταχύτητα με τη Γη η περιφορά του δηλαδή να γίνεται στο επίπεδο του Ισημερινού. Άρα είναι αδύνατον να βρίσκεται «πάνω» από οποιαδήποτε περιοχή της Γης εκτός από τα σημεία του Ισημερινού

25. Μπήπως οι παλλίρροιες δεν οφείλονται στην έλξη της Σελήνης ;

Κύριε, διάβασα ότι οι φυσικοί διατηρούν την άποψη ότι οι παλλίρροιες οφείλονται κυρίως στη βαρυτική έλξη που ασκείται στο νερό της θάλλασας από τη Σελήνη. Σκέφτηκα, ωστόσο, να υπολογίσω και την παγκόσμια έλξη που ασκεί ο Ήλιος στην ίδια ποσότητα νερού και διαπίστωσα ότι η παγκοσμια έλξη από τον Ήλιο είναι πολλές φορές πιο μεγάλη από εκείνη που ασκεί η Σελήνη. Μήπως οι παλλίρροιες οφείλονται στην παγκόσμια έλξη του Ήλιου ;

25. Ο λόγος των μαζών Ήλιου και Σελήνης είναι 27.10⁶, ενώ ο λόγος των αποστάσεων από τη Γη υψωμένος στο τετράγωνο είναι 0,15.10⁶ περίπου. Η παλλίρροια όμως δημιουργείται από τις ΟΡΙΖΟΝΤΙΕΣ συνιστώσες των δυνάμεων παγκόσμιας έλξης.

Και μολονότι η ολική δύναμη σε μια ποσότητα νερού είναι αντιστρόφως ανάλογη του ΤΕΤΡΑΓΩΝΟΥ της απόστασης, η οριζόντια συνιστώσα της είναι αντιστρόφως ανάλογη του ΚΥΒΟΥ της απόστασης. Ο λόγος των αποστάσεων υψωμένος στην τρίτη δύναμη είναι 620 .10⁶. περίπου Αυτό οδηγεί στο συμπέρασμα ότι οι προερχόμενες από τη Σελήνη οριζόντιες συνιστώσες είναι 2,3 φορές μεγαλύτερες από τις προερχόμενες από τον Ήλιο. Οι παλλίρροιες οφείλονται κατά πρώτον λόγον βαρυτική έλξη που ασκεί η Σελήνη στα νερά της θάλασσας αλλά σε μικρότερο βαθμό και στη βαρυτική έλξη που ασκεί ο Ήλιος . Αν μάλιστα τα τρία ουράνια σώματα

- Ήλιος , Σελήνη, Γη- βρεθούν σε συγκεκριμένη διάταξη, οι δύο βαρυτικές έλξεις συνεργάζονται

26. Η αθέατη πλευρά του φεγγαριού

Αναρωτιόταν «γιατί άραγε βλέπει μόνο το ένα ημισφαίριο της Σελήνης, πάντα το ίδιο ; »

26. Η Σελήνη εκτός του ότι περιφέρεται γύρω από τη Γη με περίοδο 29, 5 ημερών περίπου, έχει και τη δική της ιδιοπεριστροφή. Το ότι «ότι μας κρύβει μόνιμα τη μία της όψη» ερμηνεύεται με βάση το γεγονός ότι ΣΥΓΧΡΟΝΙΖΕΙ ΤΗΝ ΙΔΙΟΣΤΡΟΦΙΚΗ ΤΗΣ ΚΙΝΗΣΗ ΜΕ ΤΗΝ ΤΡΟΧΙΑΚΗ ΚΙΝΗΣΗ ΓΥΡΩ ΑΠΌ ΤΟ ΓΗ. Και εφόσον χρειάζεται τον ίδιο ακριβώς χρονο – 29,5 ημέρες – για να ολοκληρώσει τις δύο κινήσεις μας παρουσιάζεται πάντα με την μία μόνο όψη της.

Για να κατανοήσουμε το τι ακριβώς συμβαίνει παρουσιάζουμε το παρακάτω σχήμα. Η Σελήνη περιφέρεται σε τροχιά με περίοδο Τ_π γύρω από τη Γη και συγχρόνως εκτελεί ιδιοπεριστροφή με περίοδο Τ_πρ περί άξονα κάθετο στο σχήμα .

Εστιάζουμε την προσοχή μας στη διάμετρο της Σελήνης αβ και στην ευθεία ε των κέντρων Γης – Σελήνης.

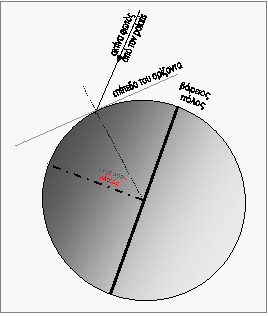
Ας θεωρήσουμε ως αρχή των χρόνων την κατώτερη, στο σχήμα, θέση της Σελήνης - όπου η φωτεινή πλευρά της κοιτάζει προς τη Γη ( για τους γήινους πανσέληνος ) - η διάμετρος αβ είναι κάθετη στην ευθεία ε .

Τη χρονική στιγμή t = T_π/4 ( μετά από ¼ της περιόδου περιφοράς Τ_π ) η διάμετρος αβ βρίσκεται ακριβώς στην ίδια ευθεία με την ε , έχει δηλαδή στραφεί ακριβώς κατά το ¼ της περιόδου ιδιοπεριστροφής Τ_πρ της Σελήνης και οι γήινοι κοιτάζοντας τον νυχτερικό ουρανό βλέπουν τη μισή Σελήνη -στη δική τους θεώρηση προς τα δεξιά -και αυτό που βλέπουν είναι τμήμα της ίδιας πλευράς που έβλεπαν στην πανσέληνο.

Τη χρονική στιγμή t = T_π/2 η διάμετρος αβ έχει στραφεί ακριβώς τόσο ώστε να γίνει και πάλι ακριβώς κάθετος στην ευθεία ε αλλά η πλευρά η λεγόμενη αθέατη είναι τώρα σκοτεινή. Τη χρονική στιγμή t = 3Τ_π /4 η διάμετρος αβ έχει γίνει ακριβώς κάθετος στην ευθεία ε και οι γήινοι βλέπουν τη μισή Σελήνη στη δική τους θεώρηση προς τα αριστερά.

Τη χρονική στιγμή t = Τ_π , η Σελήνη ξαναβρίσκεται στην αρχική θέση και η διάμετρος αβ έχει στραφεί τόσο ώστε να είναι και πάλι ακριβώς κάθετος στην ευθεία ε . Για να συμβαίνει αυτό πρέπει η περίοδος περιφοράς T_π της Σελήνης γύρω από τη Γη να είναι ακριβώς ίση με την περίοδο Τ_πρ της ιδιοπεριστροφής .

Ο τέλειος αυτός συγχρονισμός δεν οφείλεται στην τύχη. Όπως η Σελήνη φουσκώνει τους ωκεανούς που πλημμυρίζουν τις παραλίες και οι άνθρωποι μιλούν για παλλίρροια, η Γη ασκεί και αυτή δυνάμεις στη Σελήνη. Και στη Σελήνη δεν υπάρχουν θάλασσες για να φουσκώσουν, αλλά οι δράσεις αυτές φουσκώνουν τη βραχώδη επιφάνειά της με συνέπεια να μην είναι απόλυτα σφαιρική. Δημιουργούνται έτσι «παλλιροικές δυνάμεις», ασκούμενες από τη Γη στη Σελήνη, οι οποίες αναχαιτίζουν την ιδιοπεριστροφή της υποχρεώντάς την να συγχρονίζει την ιδιοπεριστροφή της με την περιφορά της γύρω από τη Γη.

Την αθέατη όψη της Σελήνης την φωτογράφησε για πρώτη φορά το σοβιετικό Λούναρ 3 το 1959, ενώ την είδαν για πρώτη φορά μάτια «ανθρώπων- αμερικανών» το 1968, από το σκάφος Απόλλων 8 .

27. Το κορίτσι κάνει κούνια

Για να κερδίσει ύψος, κάθε φορά που περνά από το κατώτερο σημείο – και όχι μόνο - ενστικτωδώς τεντώνει τα πόδια σηκώνοντάς προς τα πάνω. Ρώτησε το θείο της «γιατί με αυτόν τον τρόπο διατηρείται η αιώρηση» κι εκείνος της είπε να ρωτήσει έναν φυσικό.

27. Με αυτό που κάνει, ανασηκώνει το κέντρο μάζας και αυξάνεται η δυναμική ενέργεια άρα το σώμα της προσφέρει η ενέργεια .

Το ζήτημα είναι αρκετά πιο περίπλοκο, διότι, εκτός των άλλων, πρέπει η προσφερόμενη από το σώμα της ενέργεια να μεταβιβάζεται με συγκεκριμένο ρυθμό διότι η ταλάντωση είναι εξαναγκασμένη.

28. Επιτάχυνση χωρίς εξωτερικές δυνάμεις ;

Καλλιτεχνικό πατινάζ και το παιδί από τη Σιβηρία, ο Γεβγκένι Πλάσενκα, πάνω στην παγωμένη πίστα, στρέφεται περί κατακόρυφο άξονα, κι ύστερα μαζεύει τα χέρια του μειώνει τη ροπή αδράνειας και όσοι από τους τηλεθεατές καταλαβαίνουν από Φυσική, πίσω από την εντυπωσιακή γωνιακή ταχύτητα με την οποία τώρα στρέφεται, διακρίνουν τη διατήρηση της στροφορμής. Εκείνη όμως θα ρωτήσει την άλλη μέρα τον καθηγητή: « Με το που μαζεύει ο χορευτής τα χέρια του αυξάνεται η γωνιακή ταχύτητά του χωρίς να ασκηθούν σε αυτόν εξωτερικές δυνάμεις . Μα πώς είναι δυνατόν να προκαλείται ΕΠΙΤΑΧΥΝΣΗ χωρίς εξωτερικές ΔΥΝΑΜΕΙΣ ;»

28. Το σημαντικό αυτό ερώτημα προϋποθέτει και την απάντηση σε ένα σχεδόν «ανομολόγητο ερώτημα» των μαθητών της Γ΄Λυκείου . «Από ποια άποψη ο δεύτερος νόμος για τη στροφική κίνηση με τη μορφή τ = dL/dt

αποτελεί τη γενικότερη διατύπωση του τ = Ια_γων ;».

Ο νόμος με τη μορφή τ = dL/dt είναι, εκτός των άλλων, γενικότερος και διότι καλύπτει και την περίπτωση με ροπή αδράνειας

χρονικά μεταβαλλόμενη . Αν ο άξονας περιστροφής έχει σταθερό προσανατολισμό στον χώρο οπότε μεταβάλλεται μόνο το μέτρο της γωνιακής ταχήτητας χωρίς να αλλάζει η κατεύθυνσή της ισχύει

τ = dL/dt τ = d(Ιω)/dt τ = Ιdω/dt + ωdI/dt τ = Ια_γων + ωdI/dt

Μόνο αν η ροπή αδράνειας είναι χρονικά αναλλοίωτη προκύπτει η τ = Ια_γων

Ο γενικότερος νόμος για τη στροφική κίνηση αποκαλύπτει και ένα αρκετά σοβαρό ζήτημα .

Ότι είναι δυνατόν να μεταβληθεί η γωνιακή ταχύτητα ενός στερεού ΧΩΡΙΣ ΝΑ ΑΣΚΗΘΕΙ ΣΕ ΑΥΤΟ ΕΞΩΤΕΡΙΚΗ ΔΥΝΑΜΗ, άρα και χωρίς ολική ροπή. Αν τ= 0 η σχέση γράφεται 0 = Ια_γων + ωdI/dt άρα α_γων = - ω(dI/dt)/Ι . Η απάντηση δηλαδή είναι :

Εάν σε ένα στρεφόμενο σύστημα, λόγω εσωτερικών δυνάμεων, αλλάξει η ροπή αδράνειας, θα δημιουργηθεί γωνιακή επιτάχυνση,

το στερεό θα επιταχυνθεί χωρίς τη δράση εξωτερικών δυνάμεων

29. Η στροφορμή της σφαίρας

Η ομογενής σφαίρα, μάζας m και ακτίνας R, στρέφεται με γωνιακή ταχύτητα ω περί άξονα διερχόμενο από το κέντρο της Ο.

Η ως προς Ο στροφορμή της σφαίρας είναι ίση με το 2/5 mR²ω . Πόση είναι η τιμή της στροφορμής της σφαίρας

ως προς ένα σημείο Α της επιφάνειας ;

29. Δύο υλικά σημεία με ίσες μάζες m , σε κυκλική κίνηση με την ίδια γωνιακή ταχύτητα, αντιδιαμετρικά στον ίδιο κύκλο ακτίνας R . Η ορμή του ενός και η ορμή του αλλου είναι παράλληλα διανύσματα με αντίθετες κατευθύνσεις και ίσα μέτρα . Η στροφορμή του συστήματος των δύο υλικών σημείων , ως προς το κέντρο του κύκλου, είναι ένα διάνυσμα καθετο στο επίπεδο του κύκλου με μέτρο mυ.2R. Είναι αξιοπρόσεκτο ότι η στροφορμή του συστήματος – ροπή της ορμής - έχει την ίδια τιμή ως προς οποιοδήποτε σημείο του επιπέδου. Είναι κάτι παρόμοιο με τη ροπή ζεύγους δυνάμεων .

Εύκολα μπορούμε να συμπεράνουμε ότι η στροφορμή μιας ομογενούς σφαίρας στρεφόμενης περί άξονα, διερχομενο από το κέντρο της, έχει την ίδια τιμή 2/5mR²ω ως οποιοδήποτε σημείο της επιφάνειας και όχι μόνο

30. Οι δύο φυσικοί διαφωνούν

Ο ομογενής τροχός κυλάει σε οριζόντιο έδαφος χωρίς να τον σπρώχνει κανείς κι εκείνοι συζητούν για τις ασκούμενες στον τροχό δυνάμεις εκτός από την βάρος και την κάθετη δύναμη. Λέει ο ένας : Δεν μπορεί να ασκείται καμία οριζόντια δύναμη, όπως η στατική τριβή, διότι ο τροχός σε οριζόντιο έδαφος διατηρείται η κινητική ενέργεια του τροχού. Λέει ο άλλος : Πρέπει να υπάρχει κι άλλη δύναμη διότι και σε οριζόντιο έδαφος, ακόμα και παγωμένο, ο οποιοσδήποτε τροχός κάποτε θα σταματήσει.

30. Η σχετική θεωρία για την κύλιση αναφέρεται στο μοντέλο rigid body, σύμφωνα με το οποίο το σώμα είναι μηχανικώς αναλλοίωτο

και εάν είναι σφαίρα, το σημείο επαφής με το οριζόντιο έδαφος είναι «ένα» και το ίδιο ισχύει εάν είναι μονοδιάστατος τροχός.. Εφαρμόζοντας του νόμους της κίνησης στην κύλιση του μοντέλου rigid body το οποίο διατηρείται χωρίς την παραμικρή παραμόρφωση,

η δύναμη του εδάφους ασκείται κατακόρυφα προς τα πάνω μόνο στο συγκεκριμένο σημείο επαφής και βρίσκεται στην ίδια κατακόρυφο με την βάρος η οποία διέρχεται από το κέντρο μάζας. Με βάση τους νόμους κατά την κύλιση αυτή με σταθερή ταχύτητα του κέντρου μάζας , δεν εκδηλώνεται κανενός είδους οριζόντια στατική τριβή, η ενέργεια του σώματος διατηρείται σταθερή και . . .

ο τροχός δεν θα σταματήσει ποτέ.

Στην πραγματικότητα ο τροχός δεν είναι βέβαια όπως το μοντέλο στο οποίο εφαρμόζουμε τους νόμους. Ο πραγματικός τροχός

Κατά την επαφή του με το έδαφος υφίσταται μικρές αλλοιώσεις προς την πλευρά της κίνησης, η επαφή γίνεται σε περισσότερα σημεία και η ασκούμενη κάθετη δύναμη δεν διέρχεται από το κέντρο μάζας. Η κάθετη δύναμη βρίσκεται σε μικρή – αλλά όχι μηδενική – απόσταση από την ευθεία της βάρος .Οι δύο δυνάμεις, βάρος και κάθετη δύναμη, συγκροτούν ζεύγος το οποίο λειτουργεί επιβαδυντικά . Στη μηχανολογία, η οποία ενδιαφέρεται για πραγματικούς τροχούς, η ροπή αυτού του ζεύγους λέγεται και τριβή κύλισης.

31. Η μικρότερη απόσταση για τα δύο βότσαλα.

Δύο βότσαλα εκτοξεύονται ταυτόχρονα από σημεία Α και Β στο ίδιο υψόμετρο με ταχύτητες ίσων μέτρων , το ένα, το α, με γωνία 30⁰ ως προς τον ορίζοντα και το άλλο, το β, με γωνία 60⁰ ως προς τον ορίζοντα . Οι εκτοξεύσεις γίνονται έτσι ώστε τα ένα να κατευθύνεται προς την πλευρά του άλλου και οι τροχιές να ανήκουν στο ίδιο κατακόρυφο επίπεδο. Αν τα σημεία εκτόξευσης απέχουν 10 μέτρα , ποια είναι η μικροτερη απόσταση στην οποία θα βρεθούν ;

31. Αν φανταστεί κανείς τον εαυτό του παρατηρητή «πάνω στο ένα από τα κινούμενα βλήματα, ας πούμε στο α » η 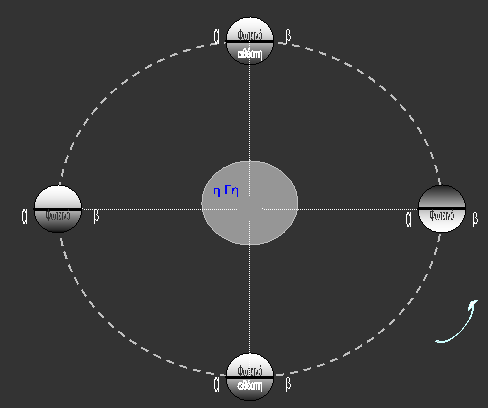τροχιά του β θα είναι ευθύγραμμη με σταθερή ταχύτητα τη σχετική ταχύτητα υ_αβ του β ως προς α τη στιγμή της εκτόξευσης. Ως παρατηρητής θα διακρίνει την ευθύγραμμη τροχιά στην ευθεία της υ_αβ. Η σχετική ταχύτητα υ_αβπροσδιορίζεται εάν αφαιρέσουμε διανυσματικά από την, ως προς το έδαφος, ταχύτητα του β, την, ως προς το έδαφος, ταχύτητα του α.

υ_αβ = υ_β- υ_α (υ_αβ , υ_β , υ_α διανύσματα) . Η ελάχιστη απόσταση θα είναι όσο η απόσταση του Α από την ευθεία της τροχιάς της σχετικής κίνησησης. d_min = 10ημ15⁰ m ημ15 = ημ(45⁰ –30⁰ ) = (√6- 2√2)/4.

Η λύση μπορεί να προκύψει και με τη μαθηματική επεξεργασία των εξισώσεων των δύο παραβολικών τροχιών ως προς το έδαφος

32. Η μύγα και το βαρίδι

Μια μύγα, πάνω σε πολύ αργό ανεμιστήρα, εκτελεί ομαλή κυκλική κίνηση 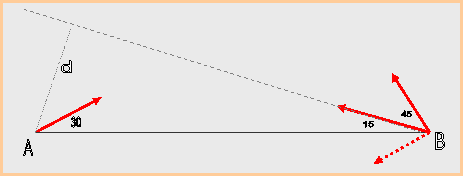ακτίνας R σε κατακόρυφο επίπεδο. Δίπλα ακριβώς στον ανεμιστήρα ένα βαρίδι εκτελεί αρμονική ταλάντωση στο ίδιο κατακόρυφο επίπεδο με πλάτος R, χωρίς να επηρεάζεται από τα ρεύμα του ανεμιστήρα. Πώς βλέπει η μύγα την κίνηση του βαριδιού εάν ο ταλαντωτής έχει την ίδια συχνότητα με εκείνη της κυκλικής κίνησης ; Να θεωρήσετε ότι σε κάποια στιγμή, η μύγα και το βαρίδι έχουν διανυσματικά ίσες ταχύτητες.

32. Θεωρούμε τόσο τη μύγα όσο και το βαρίδι υλικά σημεία . Η μέγιστη ταχύτητα της, ως προς το έδαφος, αρμονικής ταλάντωσης είναι ωR , ίση κατά μέτρο με την , ως προς το έδαφος , ταχύτητα της κυκλικής κίνησης Θεωρούμε ως αρχή των χρόνων τη στιγμή που η μύγα και το βαρίδι έχουν ίσες διανυσματικές ταχύτητες . Για τη μύγα, η σχετική ταχύτητα του βαριδιού τη στιγμή εκείνη είναι μηδέν . Μπορούμε αναλυτικά να οδηγηθούμε στο συμπέρασμα ότι η σχετική κίνηση του βαριδιού ως προς τη μύγα είναι αρμονική ταλάντωση σε οριζόντια τροχιά.