Ανδρέας Ιωάννου Κασσέτας
Παιδιά του ΚΩΝΟΥ
και της ΕΠΙΠΕΔΗΣ
Η φαντασία του ΑΠΟΛΛΩΝΙΟΥ.
Διακόσια περίπου χρόνια πριν από τον Χριστό, ο μεγάλος γεωμέτρης από την Πέργαμο «είδε» -
με το βλέμμα της σκέψης - τις ΓΡΑΜΜΕΣ που προκύπτουν κατά την τομή ενός κώνου
από επίπεδη επιφάνεια.
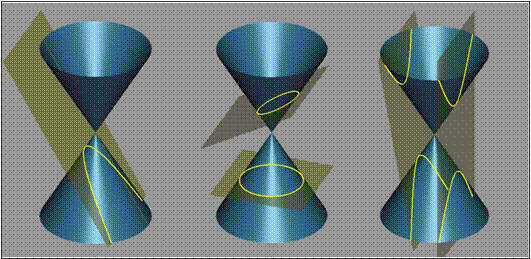 Σε
περίπωση που η επιφάνεια ειναι παράλληλη προς μια γενέτειρα του κώνου είδε την ΠΑΡΑΒΟΛΗ
.
Σε
περίπωση που η επιφάνεια ειναι παράλληλη προς μια γενέτειρα του κώνου είδε την ΠΑΡΑΒΟΛΗ
.
Σε περίπτωση που η επιφάνεια ειναι κάθετη στον
άξονα συμμετρίας του κώνου είδε τον ΚΥΚΛΟ,
ενώ εάν δεν είναι κάθετη – και δεν τέμνει τη βάση - είδε την ΕΛΛΕΙΨΗ
. Όταν η επίπεδη επιφάνεια είναι
παράλληλη προς τον άξονα του κώνου χωρίς να διέρχεται από την κορυφή ειδε την ΥΠΕΡΒΟΛΗ.
Πολλούς αιώνες αργότερα οι Ευρωπαίοι αγάπησαν τις γραμμές -παιδιά του κώνου και
της επίπεδης επιφάνειας – τις λεγόμενες ΚΩΝΙΚΕΣ ΤΟΜΕΣ - και
σε κάθε περιπτωση στη γλώσσα τους έφτιαξαν λέξεις γι αυτά βασισμένες στην
ελληνική . Εκείνοι που
τις αξιοποίησησαν ιδιαίτερα ήταν οι γεωμέτρες, οι
αστρονόμοι και οι φυσικοί. Ο Kepler,
o
Γαλιλαίος, ο Καρτέσιος και ο Νέυτων ήταν ανάμεσα στους περισσότερο ερωτευμένους
μαζί τους.




Σε γλώσσα Γεωμετρίας
η ΠΑΡΑΒΟΛΗ είναι ένα σύνολο των σημείων καθένα
από τα οποία ΙΣΑΠΕΧΕΙ
από ένα γεωμετρικό σημείο Ε ( την εστία )
και από μία ευθεία ( τη διευθετούσα )
Για το σημείο Α,
ΑΕ = ΑΑ΄, για το σημείο Β, ΒΕ= ΒΒ΄ . . .

Αν θεωρήσουμε μια
τυχαία ευθεία L
κάθετη στον άξονα συμμετρίας
έτσι ώστε η εστία
να βρίσκεται μεταξύ αυτής και της διευθετούσας,
η παραβολή είναι
και «σύνολο σημείων για καθένα απο τα οποία το άθροισμα των
αποστάσεων από την τυχαία ευθεία L
και από την εστία να είνα σταθερό» .
Αυτό ισχύει διότι
για ένα τυχαίο σημείο Α το άθροισμα ΑΕ +ΑΛ είναι ίσο με την απόσταση των
παράλληλων L και D
Υπό αυτή την
έννοια Η παραβολή είναι μια ΕΛΛΕΙΨΗ, η δεύτερη εστία της οποίας βρίσκεται στο
άπειρο.

Σε γλώσσα Αναλυτικής Γεωμετρίας
Τον 17ο αιώνα ο
Καρτέσιος μας έμαθε να αποδίδουμε σε κάθε συνάρτηση μια εικόνα .
Η ΠΑΡΑΒΟΛΗ είναι
γραφική παράσταση μιας συνάρτησης δευτέρου βαθμού y = ax2 + βx + γ.
Με κατάλληλη
επιλογή των αξόνων η συνάρτηση μπορεί να γίνει
y
= ax2
. Σε αυτή την περίπτωση η απόσταση f της εστίας Ε από την αρχή των αξόνων είναι ίση με 1/4α

Γεωμετρία της ΠΑΡΑΒΟΛΗΣ και ΦΩΣ.
Μια φωτεινή ακτίνα προερχόμενη από σημείο Ρ πέφτει
στην επιφάνεια ενός παραβολικού καθρέφτη,
ανακλάται και κατευθύνεται στην εστία Ε.
Μπορούμε να αποδείξουμε ότι για να συμβεί αυτό
πρέπει, πριν την ανάκλαση,
να είναι παράλληλη προς τον άξονα 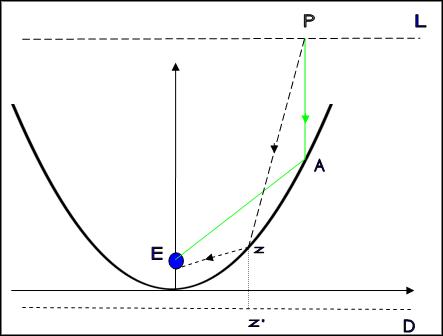 συμμετρίας
.
συμμετρίας
.
Κι αυτό διότι «υπάκουη» στην Αρχή του Fermat θα ταξιδέψει μέσα από τον χρονικά πιο
σύντομο δρόμο, ο οποίος είναι στην προκειμένη περίπτωση είναι και ο πιο μικρού
μήκους. Πράγματι από τους όλους τους δρόμους που συνδέουν – μετά από ανάκλαση –
το σημείο Ρ με την εστία Ε , ο μικρότερου μήκους είναι ο ΡΑΕ διότι είναι ίσος
με την απόσταση του Ρ από την ευθεία D.
Οποιαδήποτε άλλη διαδρομή όπως η ΡΖΑ έχει μεγαλύτερο μήκος από την ΡΑΕ .
ΡΖΕ = ΡΖΖ΄ άρα είναι μεγαλύτερη από την απόσταση του Ρ από την ευθεία D .
Το φως «υπάκουο» στην Αρχή του Fermat
θα ανακλαστεί έτσι ώστε να κατευθυνθεί στο Ε
μόνο εάν είναι παράλληλη προς τον άξονα
συμμετρίας.
Εξάλλου μόνο γι αυτή τη διαδρομή αποδεικνύεται

 ότι
η γωνία πρόσπτωσης θα είναι ίση με την
γωνία ανάκλασης.
ότι
η γωνία πρόσπτωσης θα είναι ίση με την
γωνία ανάκλασης.
Αυτό σημαίνει ότι μια φωτεινή δέσμη παράλληλη
προς τον άξονα συμμετρίας
θα ΕΣΤΙΑΣΕΙ
στο σημείο Ε.
Αυτό αξιοποιείται ιδιαίτερα σε κατοπτρικές
διατάξεις με
τις οποίες επιδιώκεται να «συγκεντρώνεται» ηλιακή
ακτινοβολία αλλά και ηλεκτρομαγνητικά κύματα που δεν είναι φως.
Ισχύει βέβαια και το αντίστροφο.
Μια σημειακή φωτεινή πηγή που θα στερεωθεί στην
εστία Ε ενός παραβολικού καθρέφτη
θα εκπέμπει φως το οποίο μετά την ανάκλαση θα
γίνεται προβολέας.
Κάτι ανάλογο συμβαίνει και με τα μακρυά φώτα των
αυτοκινήτων.

Κάτι ανάλογο μπορούμε να πετύχουμε και με κοίλους
σφαιρικούς καθρέφτες αλλά σε αυτή την περίπτωση
η εστίαση και η δημιουργία προβολέα ισχύει μόνο
για μικρού μεγέθους - σε σχέση με την
ακτίνα καμπυλότητας - σφαιρικούς καθρέφτες
με συνέπεια τεχνολογικα να υπερτερούν οι παραβολικοί
καθρέφτες.
Τι γίνεται με τους σφαιρικούς καθρέφτες ;
Αν μια φωτεινή
ακτίνα προερχομενη από την κυρία εστία ενός κοίλου ΣΦΑΙΡΙΚΟΥ καθρέφτη προσπέσει
στην επιφάνεια του με  «μικρή γωνία» – ως προς τον κύριο άξονα-
μετά την ανάκλασή της γίνεται παράλληλη προς τον κύριο άξονα.
«μικρή γωνία» – ως προς τον κύριο άξονα-
μετά την ανάκλασή της γίνεται παράλληλη προς τον κύριο άξονα.
Πόσο «μικρή»
πρέπει να είναι η γωνία
ώστε να συμβεί
αυτό;
Βασιζόμενοι στη
Γεωμετρία
μπορούμε να
αποδείξουμε ότι
ημφ= ½ ημθ
ω= θ-2φ και
p’
= R
+ Rημθ/2ημω.
Οι γωνίες θ, φ και ω παριστάνονται στο σχήμα
|
θ |
φ |
2φ |
ω |
p΄ |
|
900 |
300 |
600 |
300 |
2R |
|
600 |
25,70 |
51,30 |
8,70 |
3,86R |
|
450 |
20,70 |
41,40 |
3,60 |
6,63R |
|
300 |
14,480 |
28 ,960 |
1,040 |
14,5R |
|
200 |
9,850 |
19,690 |
0,30 |
33,4R |
|
100 |
4,980 |
9,960 |
0,040 |
131,4R |
Για να γίνει
παράλληλη η ανακλώμενη ακτίνα πρέπει θ = 2φ. Από τον πίνακα με τις ενδεικτικές
τιμές συμπεραίνουμε ότι για
θ> 20ο
η διαφορά της θ από τη 2φ είναι μετρήσιμη, ενώ για μικρότερες γωνίες θ η διαφορά μπορεί να θεωρηθεί αμελητέα.
Αυτό σημαίνει ότι από μια φωτεινή δέσμη
προερχόμενη από την εστία Ε, οι ακτίνες
 με
γωνία μεγαλύτερη των 30ο
με
γωνία μεγαλύτερη των 30ο
δεν θα συμμετέχουν στην παράλληλη δέσμη αλλά
θα συγκλίνουν σε διάφορα σημεία του άξονα.
Για να δημιουργήουμε παράλληλη δέσμη, πρέπει το
μέγεθος
του σφαιρικού κατόπτρου να έιναι τόσο ώστε μόνο
οι ακτίνες με μικρές γωνίες να προσπίπτουν σε αυτό και να ανακλώνται
Αντίθετα το
«μυστικό πλεονέκτημα » του παραβολικού είναι ότι
α. σε περίπτωση
που μια σημειακή φωτεινή πηγή βρεθεί στην εστία ένα πολύ υψηλό ποσοστό – και
ενεργειακά – του ποσοστό του φωτός θα συμβάλλει στη δημιουργία της παράλληλης
δέσμης, θ αδημιουργεί δηλαδή προβολέα.
β. Σε αντίθετη
λογική, όταν μια παράλληλη φωτεινή δέσμη
παράλληλη προς τον άξονα προσπίπτει στην ανακλαστική επιφάνεια σε ένα ιδιαίτερα
υψηλό ποσοστό ΕΣΤΙΑΖΕΤΑΙ.
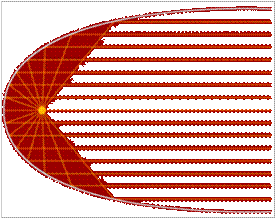

Γεωμετρία της ΠΑΡΑΒΟΛΗΣ και ΚΙΝΗΣΗ.
Ο Γαλιλαίος το είχε αποδείξει πειραματικά , αλλά ο Newton το γενίκευσε .
Όταν εκτοξεύουμε
ένα σημειακό αντικέιμενο κατακόρυφα προς τα πάνω ή προς τα κάτω η κίνηση
που θα
ακολουθήσει θα είναι ΕΥΘΥΓΡΑΜΜΗ .
Σε κάθε άλλη
περιπτωση, η τροχιά που ακολουθεί μετά
την εκτόξευση - σε ομογενές πεδίο
βαρύτητας – είναι ΠΑΡΑΒΟΛΙΚΗ ή μάλλον, επειδή παρεμβαινει και ο αόρατος αέρας,
«σχεδόν ΠΑΡΑΒΟΛΟΚΗ».
Στους αγώνες στίβου ανθρώπινα σώματα σε κίνηση και
μεταλλικά αντικείμενα ενεργοποιημένα από ανθρώπους, είτε ντοπαρισμένους είτε
καθαρούς, σώματα σε κινήσεις φαινομενικά
διαφορετικές με τη διαδρομή καθενός να προσδιορίζεται από τη διανυσματική
ταχύτητα στην αρχή της προσπάθειας, από την παρέμβαση της βαρύτητας και  από
την συνήθως λιγότερο σημαντική επίδραση του αέρα, ένα
«παιχνίδι» σωμάτων και μεταλλικών αντικειμένων με τη βαρύτητα, με στόχο τα
αντικείμενα να πάνε όσο γίνεται πιο μακριά και τα σώματα να μετατοπιστούν όσο
γίνεται περισσότερο είτε στον x τον οριζόντιο είτε στον z τον κατακόρυφο, κινήσεις που μπορεί να
μας φαίνονται διαφορετικές αλλά έρχονται
ο φυσικοί και μας λένε ότι σε όλες τις μορφές των αλμάτων και των ρίψεων
ένα αόρατο γεωμετρικό σημείο διαγράφει
την ίδια μορφή τροχιάς, μια γραμμή που σε όλες περιπτώσεις έχει την ίδια μορφή
.
από
την συνήθως λιγότερο σημαντική επίδραση του αέρα, ένα
«παιχνίδι» σωμάτων και μεταλλικών αντικειμένων με τη βαρύτητα, με στόχο τα
αντικείμενα να πάνε όσο γίνεται πιο μακριά και τα σώματα να μετατοπιστούν όσο
γίνεται περισσότερο είτε στον x τον οριζόντιο είτε στον z τον κατακόρυφο, κινήσεις που μπορεί να
μας φαίνονται διαφορετικές αλλά έρχονται
ο φυσικοί και μας λένε ότι σε όλες τις μορφές των αλμάτων και των ρίψεων
ένα αόρατο γεωμετρικό σημείο διαγράφει
την ίδια μορφή τροχιάς, μια γραμμή που σε όλες περιπτώσεις έχει την ίδια μορφή
.
Το αόρατο σημείο
είναι το κέντρο μάζας κάθε
σώματος και κάθε  μεταλλικού
αντικειμένου, το κέντρο μάζας του ανθρώπινου σώματος είτε ανήκει σε κατάξανθο
Άγγλο άλτη του μήκους, είτε σε γυναίκα με μαύρη επιδερμίδα, το
κέντρο μάζας οποιουδήποτε από τα εκτοξευόμενα μεταλλικά αντικείμενα - σφαιρικές
σφύρες με αλυσίδα, σφαιρικές σφαίρες χωρίς αλυσίδα, δίσκοι και «ευθύγραμμα» ακόντια - ενεργοποιημένα από γυμνασμένους
ανθρώπους και των δύο φύλων που διασχίζουν την τρίτη ή την τέταρτη δεκαετία της
ζωής τους, και οι φυσικοί να επιμένουν ότι η «αόρατη» τροχιά του αόρατου κέντρου μάζας είναι ήταν
και θα είναι πάντα παραβολική
μεταλλικού
αντικειμένου, το κέντρο μάζας του ανθρώπινου σώματος είτε ανήκει σε κατάξανθο
Άγγλο άλτη του μήκους, είτε σε γυναίκα με μαύρη επιδερμίδα, το
κέντρο μάζας οποιουδήποτε από τα εκτοξευόμενα μεταλλικά αντικείμενα - σφαιρικές
σφύρες με αλυσίδα, σφαιρικές σφαίρες χωρίς αλυσίδα, δίσκοι και «ευθύγραμμα» ακόντια - ενεργοποιημένα από γυμνασμένους
ανθρώπους και των δύο φύλων που διασχίζουν την τρίτη ή την τέταρτη δεκαετία της
ζωής τους, και οι φυσικοί να επιμένουν ότι η «αόρατη» τροχιά του αόρατου κέντρου μάζας είναι ήταν
και θα είναι πάντα παραβολική
όπως εκείνη που
διέκρινε για πρώτη φορά
ο Γαλιλαίος στη
μπίλια, τότε που την άφηνε να κυλήσει στο δικό του εκείνο
εργαστήριο, μια
γραμμή που η εικόνα της πλησιάζει σε εκείνη που μας
προσφέρουν τα
σιντριβάνια και οι μαθηματικοί, όταν μας μιλούν για την τομή
ενός κώνου από ένα
επίπεδο παράλληλο προς τη γενέτειρα
η μαθηματική
παραβολή στην οποία πλησιάζει η τροχιά του κέντρου μάζας
των κινουμένων
σωμάτων στις ρίψεις και στα άλματα, και την «πλησιάζει» γιατί μαθηματική
παραβολή δεν είναι ποτέ,
η γεωμετρική της
μορφή, η παραβολικότητα της, υπονομεύεται από την παρουσία του αέρα λιγότερο
όταν υπάρχει άπνοια, περισσότερο όταν η ταχύτητα του αέρα είναι μετρήσιμη,
λιγότερο στα άλματα σε ύψος, περισσότερο στο μήκος και στον ακοντισμό.



Εβδομήντα περίπου
χιλιάδες άνθρωποι καθισμένοι στις εξέδρες τη χειροκροτούν, ο ήχος φτάνει στα
αυτιά της, η Χρυσοπηγή Δεβετζή τρέχει προς τη βαλβίδα, την πατάει με δύναμη,
εκτοξεύεται λοξά προς τα πάνω, το κέντρο μάζας του σώματος της κάνει την σχεδόν
παραβολική τροχιά σε κατακόρυφο επίπεδο, το πρόσωπο της αθλήτριας απεικονίζει
την τεράστια προσπάθεια, προσγειώνεται με το δεξί πόδι στο έδαφος, πατάει δυνατά,
οι χιλιάδες σιωπούν, η τροχιά διακόπτεται για να επαναληφθεί μια ακόμα σχεδόν
παραβολική με διαφορετική αρχική ταχύτητα, ύστερα και το δεύτερο πάτημα με το
αριστερό πόδι, μια τρίτη τροχιά για το κέντρο μάζας καθώς το σώμα της
Χρυσοπηγής ταξιδεύει τώρα πια για να συναντήσει την άμμο, το σημείο στο οποίο
θα προσγειωθεί μέσα στο σκάμμα απέχει από τη βαλβίδα 16 μέτρα και 25 εκατοστά,
οι χιλιάδες διακρίνουν ότι επίδοση είναι
εξαιρετική, ξεσπούν σε χειροκρότημα μαζί και οι κραυγές τους, η Χρυσοπηγή Δεβετζή έχει κάνει το τριπλό άλμα
με το οποίο μια ελληνίδα θα πάρει μετάλλιο από ασήμι για πρώτη φορά σε
Ολυμπιακούς αγώνες στο αγώνισμα τριπλούν. Είναι έτος 2004.
Παραβολική η τροχιά του κέντρου μάζας της μπάλας στο τρίποντο του Παπαλουκά, αγώνας μπάσκετ, άθλημα που και οι κατακόρυφες τροχιές, όπως είναι εκείνες με το γκελ της μπάλας στο έδαφος, επιτρέπονται, παραβολική η τροχιά του κέντρου μάζας στο βόλεϊ, άθλημα στο οποίο οι τροχιές με ελάχιστες εξαιρέσεις μόνο παραβολικές, κι ας φαίνονται στους θεατές περίπου ευθύγραμμες λόγω της μεγάλης ταχύτητας οι τροχιές στα καρφιά.
Ζυγίζεται
πάνω στο βατήρα, ασκεί με τα ποδιά του δύναμη έτσι που η οριζόντια σανίδα
εκτελεί ταλάντωση μαζί και εκείνος ο αθλητής των καταδύσεων καταδύτης ένα μέρος
από την ορμή και την ενέργεια του συστήματος την κρατάει για τον εαυτό του,
πρέπει να κρατήσει κάπου 400 τζάουλ
κινητικής ενέργειας γιατί θα χρειαστεί να κινηθεί προς τα πάνω και τώρα
εγκαταλείπει τον βατήρα εκτοξεύεται προς
τα πάνω και γίνεται ένα κουβάρι καθώς αρχίζει να ανεβαίνει και να περιστρέφεται
περί το κέντρο της μάζας του, το κάνει
για να ελαχιστοποιήσει τη ροπή αδράνειας
και να αυξήσει τη γωνιακή του ταχύτητα τα πράγματα εξελίσσονται τρομακτικά
γρήγορα μέσα σε δύο το πολύ δευτερόλεπτα θα έχει φθάσει στο νερό ενώ ο φυσικός
που παρακολουθεί την όλη προσπάθεια διακρίνει στην κίνηση του ανθρώπινου
σώματος ένα αόρατο γεωμετρικό σημείο να διαγράφει παραβολική τροχιά. Είναι το κέντρο μάζας του
πρωταθλητή των καταδύσεων.
Η παραβολική τροχιά σε οριζόντια βολή
Ένα σημειακό αντικείμενο
εκτοξεύεται οριζόντια με ταχύτητα υ0 .
Ο Γαλιλαίος και η ΘΕΣΗ
O Galileo Galilei ήταν
ο πρώτος που μας δίδαξε – αγνοώντας την αντίσταση του αέρα –
να προσδιορίζουμε τη τη θέση του σε κάθε
μελλοντική χρονική στιγμή
 Την κίνηση που ακολουθεί τη θεώρησε σύνθεση
Την κίνηση που ακολουθεί τη θεώρησε σύνθεση
α. της
κίνησης που θα έκανε το αντικείμενο αν δεν υπήρχε βαρύτητα ( ΕΥΘΥΓΡΑΜΜΗΣ ΟΜΑΛΗΣ )
β. της κίνησης που θα έκανε το αντικείμενο αν δεν
είχε ταχύτητα και αφηνόταν ελεύθερο ( ΟΜΑΛΑ ΕΠΙΤΑΧΥΝΟΜΕΝΗΣ με επιτάχυνση g )
και με βάση την Αρχή
της Ανεξαρτησίας των κινήσεων η μετά χρονικό διάστημα t θέση
του προσδιορίζεται εάν το φανταστούμε να εκτελεί
α. την ευθύγραμμη
ομαλή επί χρόνο t , οπότε
προσδιορίζεται έτσι ένα σημείο Γ που απέχει από το σημείο βολής υ0t και στη συνέχεια – από το σημείο Γ – να
εκτελεί ανεξάρτητη
β. την ομαλά
επιταχυνόμενη επί τον ίδιο χρόνο t
οπότε προσδιορίζεται ένα σημείο Δ στην κατακόρυφο που βρίσκεται το Γ και κάτω
από το Γ σε απόσταση ½gt2 .
Ο Καρτέσιος και η ΤΡΟΧΙΑ
Αξιοποιώντας την Αναλυτική Γεωμετρία του Καρτέσιου
επιλέγουμε δύο άξονες x
και y
, οπότε η θέση του αντικειμένου σε κάθε χρονική στιγμή περιγράφεται με τις δύο
συναρτήσεις x = υ0t και
y
= ½ at2
.
Από τις δύο σχέσεις με απαλοιφή του t προκύπτει
η y =
g/2υ02.
x2
Αν τη σχέση αυτή τη «διαβάσουμε» ως ΣΥΝΑΡΤΗΣΗ y = f(x) την ακούμε να μαςπεριγράφει «πόσο έχει πέσει ( y) προς τα κάτω το αντικείμενο κάθε στιγμή
που η οριζόντια μετατoπιση του είναι x» . Το σύνολο των σημείων x,y είναι δηλαδή τα σημεία
του χώρου στα οποία βρέθηκε κατά την κίνησή του .
Η μορφή της μας λέει ότι η γραφική της παράσταση είναι ΠΑΡΑΒΟΛΗ.
Μπορούμε λοιπόν να συμπεράνουμε ότι η τροχιά είναι
παραβολική.


Η ΕΣΤΙΑ της παραβολής
Η ΕΣΤΙΑ Ε
μιας παραβολής y
= ax2 βρίσκεται σε απόσταση f = 1/4α από την αρχή των αξόνων Ο. Άρα η
εστία της παραβολής 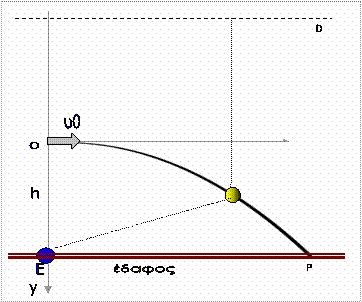 y =
g/2υ02x2
βρίσκεται σε απόσταση υ02/2g
κάτω από το σημείο εκτόξευσης, οπότε και η «διευθετούσα» D σε ύψος υ02/2g
πάνω από το σημείο εκτόξευσης. Εάν μάλιστα η εκτόξευση γίνει από ύφος h = υ02/2g πάνω από το έδαφος, η ΕΣΤΙΑ Ε θα βρίσκεται στο έδαφος και η D σε ύψος υ02/g από το έδαφος . Σε κάθε χρονική
στιγμή της κίνησης το σημειακό αντικείμενο Σ θα απέχει εξίσου από την εστία Ε
όσο απέχει από την οριζόντια διευθετούσα D. Μπορούμε
έτσι να υπολογίσουμε το «βεληνεκές» ΕΡ. Είναι ίσο με την απόσταση του Ρ από την
D. ΕΡ= υ02/g
y =
g/2υ02x2
βρίσκεται σε απόσταση υ02/2g
κάτω από το σημείο εκτόξευσης, οπότε και η «διευθετούσα» D σε ύψος υ02/2g
πάνω από το σημείο εκτόξευσης. Εάν μάλιστα η εκτόξευση γίνει από ύφος h = υ02/2g πάνω από το έδαφος, η ΕΣΤΙΑ Ε θα βρίσκεται στο έδαφος και η D σε ύψος υ02/g από το έδαφος . Σε κάθε χρονική
στιγμή της κίνησης το σημειακό αντικείμενο Σ θα απέχει εξίσου από την εστία Ε
όσο απέχει από την οριζόντια διευθετούσα D. Μπορούμε
έτσι να υπολογίσουμε το «βεληνεκές» ΕΡ. Είναι ίσο με την απόσταση του Ρ από την
D. ΕΡ= υ02/g
Μπορούμε επίσης να υπολογίσουμε το «πόσο απέχει»
το αντικείμενο από το σημείο Ε ( την προβολή του σημείου εκτόξευσης 0 στο έδαφος)
τη χρονική στιγμή στιγμή που το ύψος του έχει μειωθεί σε h/2. Η απάντηση φαίνεται απλή: Απέχει 3υ02/g όσο δηλαδή απέχει από την D.
Σε γλώσσα Γεωμετρίας
η
ΕΛΛΕΙΨΗ είναι ένα σύνολο των σημείων τα οποία το ΑΘΡΟΙΣΜΑ ΤΩΝ ΑΠΟΣΤΑΣΕΩΝ από
δύο γεωμετρικά σημεία (εστίες, E1 και E2) είναι σταθερό.

Το μέσο Ο του
ευθύγραμμου τμήματος που συνδέει τις δύο εστίες (E1, E2) λέγεται κέντρο
της έλλειψης και αποτελεί κέντρο συμμετρίας
 Κάθε ευθύγραμμο τμήμα που έχει ως άκρα δύο
διαφορετικά σημεία της έλλειψης και διέρχεται από το κέντρο αυτής λέγεται
Κάθε ευθύγραμμο τμήμα που έχει ως άκρα δύο
διαφορετικά σημεία της έλλειψης και διέρχεται από το κέντρο αυτής λέγεται
διάμετρος της έλλειψης.
Μία έλλειψη έχει
δύο άξονες συμμετρίας, οι οποίες είναι η μικρότερη και η μεγαλύτερη διάμετρός
της. O μεγάλος άξονας της έλλειψης έχει μήκος 2α, γεγονός που προκύπτει από τον
ορισμό της έλλειψης. O μικρός άξονας έχει μήκος 2β, β2 = α2 − γ2.
Ο λόγος γ/α = ε
ονομάζεται εκκεντρότητα της έλλειψης και «περιγράφει» πόσο στενή ή πόσο πλατιά
είναι η έλλειψη
Σε γλώσσα Αναλυτικής Γεωμετρίας
Τον 17ο αιώνα ο
Καρτέσιος μας έμαθε να αποδίδουμε σε κάθε συνάρτηση μια εικόνα .
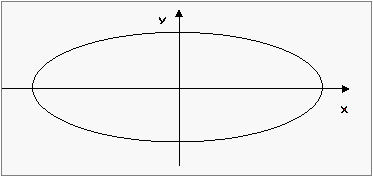 Με κατάλληλη επιλογή των αξόνων
Με κατάλληλη επιλογή των αξόνων
η ΕΛΛΕΙΨΗ
είναι γραφική παράσταση
κάθε συνάρτησης
της μορφής
x2/a2 + y2/b2 = 1 .
Εφόσον α=β
η έλλειψη γίνεται ΚΥΚΛΟΣ
Γενικότερα η
ΕΛΛΕΙΨΗ αντιστοιχεί στη συνάρτηση Αx2 + Bxy + Cy2+ Dx+Ey+F=0 με την προυπόθεση Β2
- 4ΑC
> 0
Γεωμετρία της ΕΛΛΕΙΨΗΣ και ΦΩΣ.
Να φαντασούμε έναν καθρέφτη σε σχήμα έλλειψης .
Μια οποιαδήποτε φωτεινή ακτίνα προερχόμενη από μία ΕΣΤΙΑ της έλλειψης
ανακλώμενη στοην κατοπτρική επιφάνεια θα κατευθυνθεί στην άλλη ΕΣΤΙΑ.
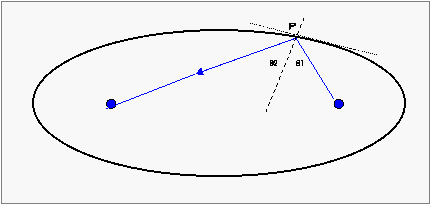
Μπορούμε να το αποδείξουμε
α. Με τους νόμους της ανάκλασης και με Αναλυτική
γεωμετρία.
Η φωτεινή ακτινα προσπίπτει στο σημείο Ρ υπό
γωνία θ1 την οποία σχηματίζει με την κάθετο στο σημείο Ρ .
 Κάθετος είναι «η κάθετος στην εφαπτομένη» στο σημείο Ρ.
Κάθετος είναι «η κάθετος στην εφαπτομένη» στο σημείο Ρ.
Σύμφωνα με τους νόμους της ανάκλασης η ανακλώμενη
ακτίνα διατηρείται στο ίδιο επίπεδο και η γωνία ανάκλασης θ2 είναι
ίση με τη γωνία πρόσπτωσης.
Με Αναλυτική γεωμετρία αποδεικνύεται
ότι η κάθετος στην εφαπτομένη
σε οποιοδήποτε σημείο Ρ μιας έλλειψης με εστίες E1
και E2 είναι διχοτόμος της
γωνίας (E1ΡE2)
β. Με την
αρχή του Fermat
Το φως διαδίδεται από τον χρονικά πιο σύντομο
δρόμο. Μια φωτεινή ακτίνα που θα βρεθεί στο σημείο E1
Για να φθάσει μετά την ανάκλαση στο σημείο Ε2
δεν έχει να επιλέξει κάποιο ειδικό δρόμο διότι όλοι οι δρόμοι που οδηγούν από
το Ε1 με ανάκλαση στην ελλειπτική κατοπτρική επιφάνεια στο σημείο Ε2
έχουν το ίδιο μήκος – το άθροισμα των δύο αποστάσεων είναι σταθερό Ε1Ρ
+ ΡΕ2 = Ε1Λ + ΛΕ2 = Ε1Μ+ ΜΕ2
- και, εφόσον η διάδοση γίνεται στο ίδιο
διαφανές μέσο, το χρονικό διάστημα του ταξιδιού είναι σταθερό. Οποιονδήποτε
λοιπόν δρομο και να ακολουθήσει η ακτίνα θα οδηγηθεί στο Ε2 .

ΕΛΛΕΙΨΗ στον ουρανό. Johannes KEPLER
Ο
Johannes KEPLER ήταν ο πρώτος που
υποστήριξε γραπτά το Κοπερνίκειο Σύστημα
( 1543) με τον ήλιο στο
κέντρο και τους πλανήτες να περιφέρονται γύρω του. Στα πλαίσια της «ΗΛΙΟΚΟΚΕΝΤΡΙΚΗΣ» θεωρίας
των τέλειων ΚΥΚΛΙΚΩΝ  ΤΡΟΧΙΩΝ εργάστηκε
σκληρά στην Πράγα - όπου βρέθηκε μετά το
1600 –πάνω στο συγκεντρωμένο υλικό των αστρονομικών παρατηρήσεων του Tycho Brahe. Ύστερα από έξι χρόνια
επεξεργασίας
αυτού του υλικού
ο Kepler κατάλαβε ότι σοβαρά ερωτήματα θα έμεναν αναπάντητα
εφόσον δεχόταν να παραμένει εγκλωβισμένος μέσα στο δόγμα της τέλειας ΚΥΚΛΙΚΗΣ
κίνησης των ουράνιων σωμάτων.
ΤΡΟΧΙΩΝ εργάστηκε
σκληρά στην Πράγα - όπου βρέθηκε μετά το
1600 –πάνω στο συγκεντρωμένο υλικό των αστρονομικών παρατηρήσεων του Tycho Brahe. Ύστερα από έξι χρόνια
επεξεργασίας
αυτού του υλικού
ο Kepler κατάλαβε ότι σοβαρά ερωτήματα θα έμεναν αναπάντητα
εφόσον δεχόταν να παραμένει εγκλωβισμένος μέσα στο δόγμα της τέλειας ΚΥΚΛΙΚΗΣ
κίνησης των ουράνιων σωμάτων.
Ήταν
ο πρώτος ερευνητής που υποστήριξε ότι η «ιερή
κυκλική κίνηση δεν είναι κυκλική» και εισηγήθηκε ότι είναι κίνηση σε τροχιά με
σχήμα ΕΛΛΕΙΨΗΣ.
Στο Astronomia Nova
το 1609 υποστήριξε ότι
1. Οι πλανήτες
περιφέρονται γύρω από τον Ήλιο σε επίπεδες τροχιές. Κάθε τροχιά έχει το σχήμα
μιας έλλειψης στη μία εστία της οποίας βρίσκεται ο Ήλιος
πρόταση η οποία
αργότερα θα κωδικοποιηθεί ως
Erstes keplersches Gesetz, Πρώτος Νόμος του Κέπλερ
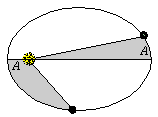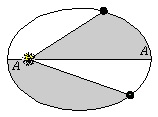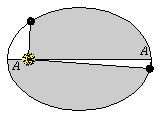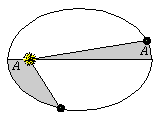
2.
Τα εμβαδά που διαγράφονται από το ευθύγραμμο τμήμα «Ήλιος- πλανήτης» είναι
ανάλογα προς τονη χρόνο που διαγράφονται.
πρόταση η οποία
αργότερα θα κωδικοποιηθεί ως Zweites
keplersches Gesetz , Δεύτερος Νόμος του Κέπλερ

Στα χρόνια που ακολούθησαν, κινούμενος στο
εσωτερικό μιας αντίληψης για την Αρμονία του Κόσμου και με ένα είδος πίστης στη
λεγόμενη Μουσική των Σφαιρών οδηγήθηκε
στη διατύπωση και του τρίτου νόμου τον οποίο παρουσίασε στο Harmonices Mundi το έτος 1619.
3.
Τα τετράγωνα των περιόδων της περιφοράς γύρω από τον Ήλιο είναι ανάλογα με τους
κύβους των μεγάλων αξόνων των ελλείψεων
πρόταση η οποία
αργότερα θα κωδικοποιηθεί ως Drittes
keplersches Gesetz,
Τρίτος Νόμος του Κέπλερ
Το έργο του Kepler υπήρξε ένα από τα σημαντικότερα στηρίγματα στη Μηχανική του Isaac Newton
O
Newton,
η ΕΛΛΕΙΨΗ και η
ΠΑΡΑΒΟΛΗ
|
Philosophiae Naturalis Principia Mathmatica BOOK 1 . The
motion of the bodies |
||
|
Σελίδα
56 PROPOSITION XI THEOREM
VI |
If a body revolves in en ellipse; it is required to find the low of the
centripetal force tending to the focus of the ellipse |
Αν ένα σώμα
κινείται σε ελλειπτική τροχιά, χρειάζεται να βρούμε τον νόμο της κεντρικής
δύναμης η οποία κατευθύνεται στο κέντρο της έλλειψης. |
|
Σελίδα 57 PROPOSITION XII THEOREM VII |
Suppose a body to move in an
hyperbola; it is required to find the low of the centripetal force
tending to the focus of that figure. |
Υποθέτουμε ότι
ένα σώμα κινείται σε μια υπερβολή.
χρειάζεται να βρούμε τον νόμο της κεντρικής δύναμης η οποία κατευθύνεται στο κέντρο
της υπερβολής. |
|
Σελίδα 60 PROPOSITION XII THEOREM VII |
If a body moves in the perimeter of a parabola ;
it is required to find the low of the centripetal force tending to the
focus of that figure. |
Αν ένα σώμα
κινείται στην περίμετρο μιας παραβολής, είναι αναγκαίο να βρούμε τον νόμο της
κεντρικής δύναμης η οποία κατευθύνεται
στο κέντρο της παραβολής. |
|
Σελίδα 65. PROPOSITION XVII PROBLEM IX |
Supposing the centripetal force to be inversely
proportional to the squares of the distances of places
from the centre, and that the absolute value of that force is known; it is
required to determine the line which the body will describe that is let from
a given place with a given velocity in the direction of a given right line. |
Υποθέτουμε ότι η
κεντρική δύναμη είναι αντιστρόφως ανάλογη προς τα τετράγωνα των αποστάσεων
των θέσεων από το κέντρο και ότι είναι η απόλυτη τιμή αυτής της δύναμης είναι
γνωστή. Χρειάζεται να προσδιορίσουμε την τροχιά – γραμμή την οποία θα
διαγράφει το σώμα με δεδομένα τη αρχική του θέση του και την γνωστής
κατεύθυνσης αρχική του ταχύτητα |
|
Σελίδα 68. SECTION IV |
To finding the elliptic, parabolic and hyperbolic
orbits, from a focus given. |
Να βρούμε την
τροχιά - ελλειπτική, παραβολική και υπερβολική-
βασιζόμενοι στο δεδομένο θέση της εστίας. |
|
Σελίδα 76. SECTION V |
How the orbits are to be found when neither focus is
given. |
Πώς θα βρεθούν (προσδιοριστούν)
οι τροχιές εάν δεν είναι δεδομένη ούτε η εστία |
|
Σελίδα 109. PROPOSITION XXX. PROBLEM XXII |
To find at any assigned time the place of a body
moving in a given parabola |
Να προσδιοριστεί
σε συγκεκριμένη στιγμή η θέση ενός σώματος κινουμένου σε δεδομένη παραβολή |
|
Σελίδα 112. PROPOSITION XXXI PROBLEM XXIII |
To find the place of a body moving in a given
ellipse at any assigned time |
Να προσδιοριστεί
σε συγκεκριμένη στιγμή η θέση ενός σώματος κινουμένου σε δεδομένη έλλειψη |
|
Philosophiae Naturalis Principia Mathmatica BOOK 3 .
The System of the Word |
||
|
Proposition XΙΙΙ. Theorem XΙΙΙ. |
Τhe
planets move in ellipses which have their common focus in the centre of the
sun; and by radii drawn to that centre, they describe areas proportional to
the time of description |
Οι πλανήτες
κινούνται σε ελλείψεις οι οποίες έχουν την κοινή τους εστία στο κέντρο
του Ήλιου και από την ακτίναπου άγεται από αυτό το κέντρο διαγράφονται εμβαδά
ανάλογα προς τους χρόνους της
διαγραφής τους. |
|
Proposition XL. Theorem XΧI . |
That the comets move in some of the conic sections,
having their foci in the centre of the sun; and by radii drawn describe areas
proportional to the times. |
Οι κομήτες
κινούνται σε κάποιες κωνικές τομές, με τις εστίες τους να βρίσκονται
στο κέντρο του Ήλιου. Και από την «επιβατική» ακτίνα διαγράφονται επιφάνειες
ανάλογες προς τους χρόνους. |
|
Proposition XLI. Problem XX. |
From three observations
given to determine the orbit of a comet moving in a parabola |
Από
τρεις δεδομένες παρατηρήσεις να προσδιοριστεί η τροχιά ενός κομήτη κινούμενου
σε παραβολή |
Το
πρόβλημα
Σε ένα σώμα - σημειακό αντικείμενο - ασκείται συνεχώς δύναμη ΚΕΝΤΡΙΚΗ -κατευθυνόμενη
δηλαδή σε ένα σταθερό σημείο- η τιμή της οποίας είναι αντιστρόφως ανάλογη προς
τα τετράγωνα των αποστάσεων των θέσεων του σώματος από το σταθερό σημείο –
κέντρο Ο . Σε μια χρονική στιγμή το αντικείμενο έχει μια ταχύτητα υ κάθετη στη
δύναμη αυτή.
Ποια θα είναι η τροχιά της κίνησής του στη
συνέχεια, εφόσον δεν ασκούνται άλλες δυνάμεις ;
Ένα «καλό» παράδειγμα είναι η κίνηση ενός
δορυφόρου στο γήινο πεδίο βαρύτητας.
Η απάντηση.
Υποθέτουμε ότι το αντικείμενο έχει μάζα και βρίσκεται σε απόσταση r από
το κέντρο.
Στο χρονικό διάστημα dt το σώμα υπό την επίδραση της κάθετης στην
ταχύτητά του δύναμης θα στρίψει
έτσι ώστε η επιβατική ακτίνα να στραφεί κατά γωνία dφ. Στο ίδιο αυτό χρονικό διάστημα dt στην αρχική ταχύτητα υ θα προστεθεί
διανυσματικά η ταχύτητα dυ
ίση με αdt
και στην κατεύθυνση της ασκούμενης κεντρικής δύναμης. Το
a
είναι η επιτάχυνση η τιμή της οποίας
διαμορφώνεται από τις τιμές της δύναμης και της μάζας .
Η νέα ταχύτητα, ως διανυσματικό άθροισμα της υ και
της dυ,
θα σχηματίζει με τη υ γωνία dθ
για την οποία dθ
= dυ/υ
= αdt/υ.
Στο ίδιο αυτό χρονικό διάστημα dt
και ενώ το διάνυσμα της ταχύτητάς του θα έχει
«στραφεί» κατά dθ,
το σώμα θα έχει διαγράψει τόξο υdt
και η
«επιβατική ακτίνα» θα έχει στραφεί κατά dφ = υdt/r
Το «τι θα
συμβεί» θα καθοριστεί από την τιμή της ταχύτητας.
α.
Εάν η τιμή της ταχύτητας είναι τόση ώστε η ποσότητα υ2/r να είναι ίση με την τιμή της επιτάχυνσης
 η
σχέση dθ
= αdt/υ
θα γίνει dθ
= υ2dt/rυ άρα
dθ
= υdt/r.
Αλλά το υdt/r είναι ίσο με τη γωνία φ κατά την οποία
έχει στραφεί η επιβατική ακτίνα . Άρα dθ = dφ.
η
σχέση dθ
= αdt/υ
θα γίνει dθ
= υ2dt/rυ άρα
dθ
= υdt/r.
Αλλά το υdt/r είναι ίσο με τη γωνία φ κατά την οποία
έχει στραφεί η επιβατική ακτίνα . Άρα dθ = dφ.
Από την ισότητα των δύο γωνιών προκύπτει ότι επιβατική
ακτίνα – άρα και η κεντρική δύναμη - θα
είναι και πάλι ΚΑΘΕΤΗ στην ταχύτητα και αυτό θα συμβαίνει
συνέχεια. Το σώμα θα κινείται χωρίς αυξομειώσεις ταχύτητας σε τροχιά
ΚΥΚΛΟΥ. Η απόστασή του από το σταθερό σημείο Ο θα
διατηρείται αναλλοίωτη άρα και το μέτρο της δύναμης θα διατηρείται σταθερό
Σε περιπτωση που πρόκειται για αντικείμενο μάζας m εκτοξευόμενο οριζόντια στο πεδίο βαρύτητας
του μάζας Μ πλανήτη Γη, σε απόσταση r από το κέντρο του πλανήτη, η ασκούμενη δύναμη θα είναι ίση με GMm/r2, οπότε η επιτάχυνση θα
είναι GM/r2 , και η προυπόθεση α = υ2/r διαμορφώνεται σε GM/r2
= υ2/r άρα υ = (GM/r)
½. Το αντικείμενο γίνεται δορυφορος σε κυκλική τροχιά.
Για το γήινο πεδίο βαρύτητας και για εκτόξευση σε χαμηλό ύψος (
r ≈ RΓης ) η τιμή (GM/r)½
ειναι περίπου 7,9 km/s.
β.
Εάν η τιμή της ταχύτητας είναι τόση ώστε
η ποσότητα υ2/r
να είναι μεγαλύτερη από την τιμή της επιτάχυνσης
η τιμή dθ = αdt/υ θα είναι μικρότερη από την υ2dt/rυ άρα και από την υdt/r. Αλλά το  υdt/r είναι ίσο με τη γωνία dφ που διαγράφει στο ίδιο διάστημα η
επιβατική ακτινα. Άρα dθ < dφ.
Η ταχύτητα «έστριψε» λιγότερο από την επιβατική ακτίνα και
αυτό σημαίνει ότι η κεντρική δύναμη δεν είναι κάθετη στην ταχύτητα. Τα δύο
διανύσματα F
και υ’ σχηματίζουν
αμβλεία γωνία. Η F
αναλύεται σε μια συνιστώσα κάθετη στην ταχύτητα η οποία θα
προκαλεί την αλλαγή στην κατεύθυνση της
ταχύτητας και σε μια συνιστώσα «επιβραδυντική» η οποία θα επιφέρει τη μείωση
της ταχύτητας. Εφόσον βέβαια η ως προς Ο ροπή είναι μηδενική, η στροφορμή του σώματος – ίση με mυd, όπου d η απόσταση το Ο από τον
κοινό φορέα ορμής και ταχύτητας –
διατηρειται, με συνέπεια η μείωση της
ταχύτητας να συνεπάγεται αύξηση της απόστασης d του
Ο από τον φορέα της ταχύτητας.
υdt/r είναι ίσο με τη γωνία dφ που διαγράφει στο ίδιο διάστημα η
επιβατική ακτινα. Άρα dθ < dφ.
Η ταχύτητα «έστριψε» λιγότερο από την επιβατική ακτίνα και
αυτό σημαίνει ότι η κεντρική δύναμη δεν είναι κάθετη στην ταχύτητα. Τα δύο
διανύσματα F
και υ’ σχηματίζουν
αμβλεία γωνία. Η F
αναλύεται σε μια συνιστώσα κάθετη στην ταχύτητα η οποία θα
προκαλεί την αλλαγή στην κατεύθυνση της
ταχύτητας και σε μια συνιστώσα «επιβραδυντική» η οποία θα επιφέρει τη μείωση
της ταχύτητας. Εφόσον βέβαια η ως προς Ο ροπή είναι μηδενική, η στροφορμή του σώματος – ίση με mυd, όπου d η απόσταση το Ο από τον
κοινό φορέα ορμής και ταχύτητας –
διατηρειται, με συνέπεια η μείωση της
ταχύτητας να συνεπάγεται αύξηση της απόστασης d του
Ο από τον φορέα της ταχύτητας.
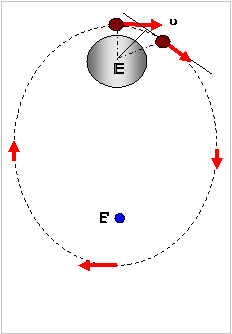
Αποδεικνύεται ότι η κίνηση που θα ακολουθήσει να
είναι σε τροχιά ΕΛΛΕΙΨΗ και με «κοντινή εστία» (Ε) το κέντρο Ο. Εάν η ταχύτητα
είναι ακόμα μεγαλύτερη η δεύτερη εστία Ε΄θα βρίσκεται ακόμα πιο μακριά. Για
ορισμένη τιμή ταχύτητας η εστία Ε΄θα βρεθεί σε άπειρη απόσταση και η τροχιά
γίνεται τμήμα ΠΑΡΑΒΟΛΗΣ.

Σε περιπτωση που πρόκειται για αντικείμενο μάζας m εκτοξευόμενο οριζόντια στο πεδίο βαρύτητας
του μάζας Μ πλανήτη Γη, σε απόσταση r από το κέντρο του πλανήτη, η ασκούμενη δύναμη θα είναι ίση με GMm/r2, οπότε η επιτάχυνση θα
είναι GM/r2 , και η προυπόθεση υ2/r > α διαμορφώνεται σε υ2/r >
GM/r2 άρα υ
> (GM/r)½ .
Το αντικείμενο γίνεται δορυφορος σε ελλειπτική τροχιά με
κοντινή εστια το κέντρο του πλανήτη. Κατά την κίνησή του διατηρείται τόσο η
στροφορμή όσο και η ενέργεια. Με βάση τη διατήρηση της ενέργειας αποδεικνύεται
ότι για ταχύτητα μεγαλύτερη από (2GM/r)½
η τροχιά γίνεται τμήμα ΠΑΡΑΒΟΛΗΣ και το αντικείμενο δεν επιστρέφει. Η
τιμή (2GM/r)½
για το γήινο πεδίο βαρύτητας είναι περίπου 11, 2 km/s. Είναι η λεγόμενη ταχύτητα διαφυγής .
γ.
Εάν η τιμή της ταχύτητας είναι τόση ώστε
η ποσότητα υ2/r
να είναι μικρότερη από την τιμή της επιτάχυνσης
η τιμή dθ = αdt/υ θα είναι μεγαλύτερη από την υ2dt/rυ άρα και από την υdt/r. Αλλά το  υdt/r είναι ίσο με τη γωνία dφ που διαγράφει στο ίδιο διάστημα η
επιβατική ακτινα. Άρα dθ > dφ. Η ταχύτητα «έστριψε»
περισσότερο από την επιβατική ακτίνα και αυτό σημαίνει ότι η κεντρική δύναμη
δεν είναι κάθετη στην ταχύτητα. Τα δύο διανύσματα F και
υ’ σχηματίζουν οξεία γωνία. Η F αναλύεται
σε μια συνιστώσα κάθετη στην ταχύτητα η οποία θα προκαλεί την αλλαγή στην
κατεύθυνση της ταχύτητας και σε μια
συνιστώσα «επιταχυντική» η οποία θα επιφέρει αύξηση της ταχύτητας. Εφόσον
βέβαια η ως προς Ο ροπή είναι μηδενική, η στροφορμή του σώματος – ίση με mυd, όπου d η απόσταση το Ο από τον
κοινό φορέα ορμής και ταχύτητας –
διατηρειται, με συνέπεια η αύξηση της
ταχύτητας να συνεπάγεται μείωση της απόστασης d του
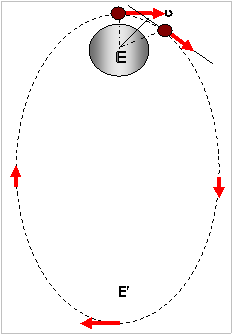
Ο από τον φορέα της ταχύτητας. Αποδεικνύεται ότι η κίνηση που θα ακολουθήσει να
είναι σε τροχιά ΕΛΛΕΙΨΗ έτσι ώστε το κέντρο Ο στο οποίο κατευθύνεται η δύναμη
να είναι η «μακρινή εστία»
υdt/r είναι ίσο με τη γωνία dφ που διαγράφει στο ίδιο διάστημα η
επιβατική ακτινα. Άρα dθ > dφ. Η ταχύτητα «έστριψε»
περισσότερο από την επιβατική ακτίνα και αυτό σημαίνει ότι η κεντρική δύναμη
δεν είναι κάθετη στην ταχύτητα. Τα δύο διανύσματα F και
υ’ σχηματίζουν οξεία γωνία. Η F αναλύεται
σε μια συνιστώσα κάθετη στην ταχύτητα η οποία θα προκαλεί την αλλαγή στην
κατεύθυνση της ταχύτητας και σε μια
συνιστώσα «επιταχυντική» η οποία θα επιφέρει αύξηση της ταχύτητας. Εφόσον
βέβαια η ως προς Ο ροπή είναι μηδενική, η στροφορμή του σώματος – ίση με mυd, όπου d η απόσταση το Ο από τον
κοινό φορέα ορμής και ταχύτητας –
διατηρειται, με συνέπεια η αύξηση της
ταχύτητας να συνεπάγεται μείωση της απόστασης d του
Ο από τον φορέα της ταχύτητας. Αποδεικνύεται ότι η κίνηση που θα ακολουθήσει να
είναι σε τροχιά ΕΛΛΕΙΨΗ έτσι ώστε το κέντρο Ο στο οποίο κατευθύνεται η δύναμη
να είναι η «μακρινή εστία»
Σε περιπτωση που πρόκειται για αντικείμενο μάζας m εκτοξευόμενο οριζόντια στο πεδίο βαρύτητας
του μάζας Μ πλανήτη Γη, σε απόσταση r από το κέντρο του πλανήτη, η ασκούμενη δύναμη θα είναι ίση με GMm/r2, οπότε η επιτάχυνση θα
είναι GM/r2 , και η προυπόθεση υ2/r < α διαμορφώνεται σε υ2/r <
GM/r2 άρα υ
< (GM/r)½ .
Το αντικείμενο «είναι δυνατόν να γινει δορυφορος σε
ελλειπτική τροχιά με μακρινή εστία το κέντρο του πλανήτη.
Εάν η εκτόξευση γινει με πολύ μικρότερη ταχύτητα
και από ύψος μικρό σχετικά με την ακτινα του πλανήτη η τροχιά θα
συναντήσει την επιφάνεια του πλανήτη, το
αντικειμενο θα πέσει στο έδαφος.
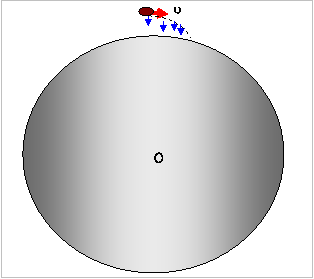
Εφόσον μάλιστα το ύψος είναι πολύ μικρό σε σχέση
πάντοτε με την ακτίνα του πλανήτη, η μακρινή εστία της έλλειψης – το κέντρο
δηλαδή της Γης - θα μπορεί να θεωρηθεί ότι βρίσκεται στο άπειρο, η τροχιά θα μπορεί να θεωρηθεί τμήμα
ΠΑΡΑΒΟΛΗΣ και το αντικείμενο θα φθάσει
στο έδαφος. Σε αυτή την περίπτωση κατά την οποία το κέντρο Ο της
«κεντρικής» δύναμης θα βρίσκεται στο άπειρο πράγμα που σημαίνει ότι οι
ασκούμενες σε κάθε θέση δυνάμεις – καθεμια είναι το βάρος του σώματος - μπορούν
να θεωρηθούν παράλληλες και ίσες μεταξύ τους και το πεδίο βαρύτητας να θεωρηθεί
ομογενές.
Τέτοιου είδους τροχιά είναι και η γνωστή ΠΑΡΑΒΟΛΗ
την οποία
διαπιστώνουμε εκτοξεύοντας οριζόντια
αντικειμενα ως άνθρωποι του συγκεκριμένου πλανήτη

Στις γλώσσες του Κόσμου.
Parabola οι
Αγγλοι, οι Νορβηγοί, οι Φιλιππινέζοι
οι Ιταλοί, οι Ούγγροι, οι Κροάτες, οι Σλοβένοι, οι Τσέχοι
οι Σλοβάκοι, οι
Πολωνοί, οι Λιθουανοί, οι Λετονοί
Parábola οι
Ισπανοί, οι Πορτογάλοι Parabolă οι Ρουμάνοι
Parabole οι Γάλλοι
Parabel οι
Γερμανοί
Parabelns οι Σουηδοί
Parabοοl οι Ολλανδοί, οι Εσθονοί
Parabol οι Δανοί, οι Τούρκοι Parabolë οι Αλβανοί
Paraabeli οι Φιλανδοί
Парабола
οι Ρώσοι, οι Σέρβοι, οι Βούλγαροι, οι
Ουκρανοί
Ellipse
οι Αγγλοι, οι Γάλλοι , οι Γερμανοί, οι Δανοί,
οι Ισπανοί, οι
Πορτογάλοι οι Νορβηγοί, οι Λετονοί
Ellipsa
οι Τσέχοι, οι Πολωνοί, οι Κροάτες,
οι Σλοβένοι, οι Λιθουανοί
Ellips
οι Ολλανδοί, οι Εσθονοί οι
Σουηδοί Elips οι Τούρκοι, οι Αλβανοί
Ellisse
οι Ιταλοί Ellissι
οι Μαλτέζοι
Ellipsy
οι Σλοβάκοι Elipsă οι
Ρουμάνοι
Эллипс οι Ρώσοι Еліпс οι Ουκρανοί Елипса οι
Βούλγαροι Елипсу οι
Σέρβοι
Ellipsi
οι
Φιλανδοί Elipziz οι Ούγγροι Ellips
οι Ινδονήσιοι Tambilugan οι Φιλιππινέζοι