Ανδρέας Ιωάννου Κασσέτας

( Σε όλα τα προβλήματα - εκτός από το 9 - στα οποία υπεισέρχεται βαρύτητα να θεωρήσετε την τιμή της βαρυτικής επιτάχυνσης ίση με και 10 m/s² , Να θεωρήσετε επίσης για την τιμή του π ότι π² = 10 )

1. Ένα αντικείμενο εκτελεί αρμονική ταλάντωση πλάτους 50cm. Όταν η απομάκρυνση του αντικειμένου είναι +30cm, η ταχύτητά του είναι +4m/s. Να υπολογίσετε την περίοδο της ταλάντωσης και το μέτρο της ταχύτητας του αντικειμένου όταν η θέση του είναι +40cm

2. Ένα αντικείμενο εκτελεί αρμονική ταλάντωση με περίοδο 10s και πλάτος 20cm. Κατά τη χρονική στιγμή μηδέν βρίσκεται στη θέση ισορροπίας κινούμενο προς τον θετικό ημιάξονα. Να υπολογίσετε επί πόσο χρόνο – κατά τη διάρκεια της πρώτης περιόδου – η απομάκρυνση του θα είναι μεγαλύτερη από +10cm.

3. Ένα αντικείμενο εκτελεί αρμονική ταλάντωση με περίοδο 0,2π s. Κατά τη χρονική στιγμή μηδέν το αντικείμενο κατευθύνεται προς τη θέση ισορροπίας και βρίσκεται σε θέση (απομάκρυνση) +4cm με μέτρο ταχύτητας 40√3 cm/s.

Να γράψετε τις εξισώσεις θέσης, ταχύτητας και επιτάχυνσης συναρτήσει του χρόνου.

4. Ένα υλικό σημείο εκτελεί απλή αρμονική ταλάντωση πλάτους 10 cm. Κατά τη χρονική στιγμή τη θεωρούμενη ως αρχή των χρόνων η απομάκρυνσή του είναι 0,05 m και η ταχύτητά του – √3 m/s.

α. Να προσδιορίσετε τη θέση του αντικειμένου κατά τη χρονική στιγμή π/5 s.

β. Να προσδιορίσετε την επιτάχυνση κατά την αρχή των χρόνων.

γ. Να παραστήσετε γραφικά τη δύναμη επαναφοράς σε συνάρτηση με την απομάκρυνση αν είναι γνωστό ότι η μάζα του αντικειμένου είναι 100 g.

5. Δύο σώματα Σ₁ και Σ₂ με ίσες μάζες ισορροπούν κρεμασμένα από κατακόρυφα ιδανικά ελατήρια με σταθερές k₁ και k₂ που συνδέονται με τη σχέση k₁ = k₂ /2. Απομακρύνουμε τα σώματα Σ₁ και Σ₂ από τη θέση ισορροπίας τους κατακόρυφα προς τα κάτω κατά x και 2x αντίστοιχα και τα αφήνουμε ελεύθερα την ίδια χρονική στιγμή, οπότε εκτελούν απλή αρμονική ταλάντωση. Τα σώματα διέρχονται για πρώτη φορά από τη θέση ισορροπίας τους:

α. ταυτόχρονα β. σε διαφορετικές χρονικές στιγμές με πρώτο το Σ₁

γ. σε διαφορετικές χρονικές στιγμές με πρώτο το Σ₂

6. Ένα ελατήριο, με φυσικό μήκος 14 cm, έχει σταθερά 200N/m. Διατηρούμε το ελατήριο κατακόρυφο με το ανώτερο άκρο του ακινητοποιημένο και στο κάτω άκρο του κρεμάμε ένα σφαιρίδιο, οπότε το σύστημα ισορροπεί και διαπιστώνουμε ότι το μήκος του τεντωμένου ελατηρίου είναι τώρα 18 cm. Στη συνέχεια ενεργοποιούμε το σύστημα έτσι ώστε το σφαιρίδιο να εκτελεί κατακόρυφη ταλάντωση και διαπιστώνουμε ότι το μεγαλύτερο μήκος που αποκτά το ελατήριο είναι 24 cm. Δίνεται ότι g = 10 m / s² .

Σας ζητούμε α. να υπολογίσετε τη συχνότητα της ταλάντωσης

β. να υπολογίσετε τη μέγιστη κινητική ενέργεια του σφαιριδίου κατά τη διάρκεια της ταλάντωσης

γ. να κάνετε τη γραφική παράσταση δυναμικής ενέργειας και απομάκρυνσης

7. Ένα σώμα Σ μάζας 2 kg και αμελητέων διαστάσεων διατηρούμενο πάνω σε οριζόντια επιφάνεια με αμελητέα τριβή προσδένεται από την αριστερή πλευρά σε ένα ελατήριο Ε₁ σταθεράς 120N/m και φυσικού μήκους 14 cm από τη δεξιά του πλευρά και σε ένα άλλο ελατήριο Ε₂ σταθεράς 80N/m και φυσικού μήκους 14 cm. Το άλλο ελεύθερο άκρο κάθε ελατηρίου προσδένεται σε αντίστοιχο τοίχωμα, έτσι ώστε τα ελατήρια να διατηρούνται οριζόντια. Όταν το σώμα είναι ακίνητο το ελατήριο Ε₂ έχει μήκος 17 cm.

α. Na προσδιορίσετε κατά πόσο είναι τεντωμένο το ελατήριο Ε₁, εφόσον το σώμα Σ ισορροπεί.

Ενεργοποιούμε το σύστημα έτσι ώστε το σώμα Σ να εκτελέσει οριζόντια ταλάντωση και το ελάχιστο μήκος του Ε₂ να είναι 13 cm. Θεωρούμε ως αρχή των χρόνων τη χρονική στιγμή που το σώμα Σ βρίσκεται στη θέση ισορροπίας κινούμενο προς τα δεξιά.

β. Να αποδείξετε ότι η ταλάντωση θα είναι αρμονική γ. Να υπολογίσετε την περίοδο Τ της ταλάντωσης.

δ. Να υπολογίσετε τη μέγιστη κινητική ενέργεια του σώματος Σ κατά τη διάρκεια της ταλάντωσής του

ε. Να προσδιορίσετε το μήκος κάθε ελατηρίου κατά τη χρονική στιγμή Τ/12.

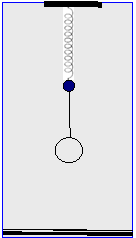
8. Σε κάποια στιγμή κόβεται το νήμα που συνδέει τη μικρή σφαίρα Σ (πάνω) με τη μεγαλύτερη σφαίρα Σ΄.

Η Σ΄ πέφτει προς το έδαφος, ενώ η Σ, στο άκρο του κατακόρυφου ελατηρίου τίθεται σε ταλάντωση.

Τη στιγμή που η Σ΄ φθάνει στο έδαφος η Σ επανέρχεται στην αρχική της θέση για έβδομη φορά. Να υπολογίσετε τη μέγιστη κινητική ενέργεια της Σ κατά τη διάρκεια της ταλάντωσης. Δίνονται η μάζα της 50g, η μάζα της Σ΄100 g, το ύψος της Σ΄ από το έδαφος 2 m και g = 10m/s². Οι σφαίρες να θεωρηθούν υλικά σημεία

"

9. Διαθέτουμε ένα βαρίδι κι ένα ελατήριο και βρισκόμαστε σε τόπο με βαρύτητα και άγνωστη την τιμή της βαρυτικής επιτάχυνσης. Να προτείνετε έναν τρόπο μέτρησης της βαρυτικής επιτάχυνσης – εκτός από εκείνον με την ελεύθερη πτώση - εάν διαθέτουμε μία ΜΕΤΡΟΤΑΙΝΙΑ και ένα ΧΡΟΝΟΜΕΤΡΟ . Να συγκρίνετε την ακρίβεια της μιας μέτρησης με την ακρίβεια της άλλης.

10. Βρισκόμαστε σε ένα διαστημικό σκάφος σε περιοχή με μη ανιχνεύσιμη βαρύτητα. Πώς θα μπορούσαμε να μετρήσουμε τη μάζα ενός αντικειμένου; Διαθέτουμε μία μετροταινία, ένα χρονόμετρο, ένα ελατήριο γνωστής σταθεράς στο οποίο μπορούμε να προσδέσουμε το αντικείμενο και ένα νήμα στο οποίο μπορούμε επίσης να προσδέσουμε το αντικείμενο.

11. Ζυγίζοντας με χρονόμετρο. Στο άκρο κατακόρυφου ελατηρίου κρέμεται δίσκος και η περίοδος του ταλαντωτή είναι 2,3 s . Αν προσθέσουμε στο δίσκο αντικείμενο Σ₁ βάρους 8Ν, η περίοδος γίνεται 2,6. Αν αντικαταστήσουμε το αντικείμενο Σ₁ με αντικείμενο Σ₂ η περίοδος γίνεται 3,2 s. Πόσο είναι το βάρος του Σ₂;

12. Το μικρό κιβώτιο Σ ακινητεί στο άκρο του ελατηρίου όπως στο σχήμα. Ένα παρόμοιο κιβώτιο Σ΄ τοποθετείται δίπλα στο Σ και το σύστημα αφήνεται ελεύθερο. Να βρείτε σε πόσο χρόνο τα δύο κιβώτια κινούμενα προς τα κάτω θα φθάσουν στο κατώτερο σημείο καθώς και πόσο θα έχουν μετακινηθεί από το σημείο στο οποίο αφήνονται ελεύθερα.

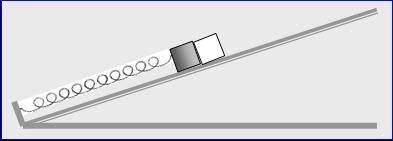Δίδονται η σταθερά του ελατηρίου k , η μάζα κάθε κιβωτίου m,

η γωνία του κεκλιμένου επιπέδου θ, και η βαρυτική επιτάχυνση g. Η τριβή θεωρείται αμελητέα.

13. Ένα σώμα Σ αμελητέων διαστάσεων βρίσκεται σε οριζόντιο τραπέζι, με αμελητέα τριβή. Από τη μία πλευρά το σώμα συνδέεται με οριζόντιο ελατήριο σταθεράς k₁ = 100 N/m και φυσικού μήκους 18 cm το άλλο άκρο του οποίου στερεώνεται σε κατακόρυφο τοίχωμα ενώ από την άλλη πλευρά το ίδιο σώμα συνδέεται με ένα άλλο οριζόντιο ελατήριο σταθεράς k₂ = 300 N/m και φυσικού μήκους 18 cm το άλλο άκρο του οποίου στερεώνεται σε κατακόρυφο τοίχωμα απέναντι από το προηγούμενο. Τα δύο τοιχώματα απέχουν 44 cm.

a. Να υπολογίσετε το μήκος κάθε ελατήριου κατά την ισορροπία του Σ.

Το σώμα Σ ενεργοποιείται με 2 τζάουλ έτσι ώστε να κινείται στο οριζόντιο τραπέζι και η μέγιστη τιμή της ταχύτητάς του να είναι 2 m/s.

β. Να υπολογίσετε τη μάζα του σώματος και το πλάτος της ταλάντωσης

Σε κάποια χρονική στιγμή κατά την οποία το σώμα διέρχεται από τη θέση ισορροπίας πέφτει πάνω του ένα κομμάτι λάσπη - κινούμενο μέχρι εκείνη τη στιγμή κατακόρυφα - μάζας 200 g που προσκολλάται σ΄ αυτό. Σας ζητούμε να υπολογίσετε γ. Μετά πόσον χρόνο μετά την προσκόλληση το συσσωμάτωμα θα βρεθεί για πρώτη φορά στην ακραία θέση της ταλάντωσής του καθώς και δ. το πλάτος της ταλάντωσης του συσσωματώματος;

14. Ένας δίσκος μάζας 200 g ισορροπεί στο άκρο ελατηρίου σταθεράς 200 N/m . Ένα σώμα μάζας 200 g αφήνεται από ύψος 80 cm πάνω από τον δίσκο, προσπίπτει στο κέντρο του δίσκου και προσκολλάται σ’ αυτόν . Να υπολογίσετε την περίοδο και το πλάτος της ταλάντωσης του συσσωματώματος.

15. Ένας δίσκος μάζας 200 g ισορροπεί στο άκρο ελατηρίου σταθεράς 20 N/m . Ένα σώμα μάζας 200 g αφήνεται από ύψος π²/20 m πάνω από το κέντρο του δίσκου και συγκρούεται ελαστικά με τον δίσκο. Να προσδιορίσετε :

α. πόσο χαμηλά θα φθάσει ο δίσκος

β. που θα βρίσκεται ο δίσκος τη στιγμή που το σώμα θα έχει φθάσει στο ανώτερο σημείο της τροχιάς του

16. Ένα βαρίδι Σ₁ μάζας 400 g εκτελεί αρμονική ταλάντωση στο άκρο κατακόρυφου ελατηρίου . Η σταθερά του ελατηρίου είναι 40 N/m και το φυσικό του μήκος 22 cm . Το μέγιστο μήκος του ελατηρίου κατά τη διάρκεια της ταλάντωσης είναι 37 cm . Να υπολογίσετε : α. την μέγιστη τιμή της ταχύτητας του Σ₁ και

β. το ελάχιστο μήκος του ελατηρίου κατά τη διάρκεια της ταλάντωσης

Σε κάποια χρονική στιγμή, που το μήκος του ελατηρίου είναι 35 cm και το Σ₁ κινείται προς τα κάτω, ένα αντικείμενο μάζας 400 g κινούμενο προς τα κάτω με ταχύτητα 0,2 m/s συγκρούεται με το βαρίδι και προσκολλάται σε αυτό . Το συσσωμάτωμα εκτελεί στη συνέχεια αρμονική ταλάντωση με μικρότερη συχνότητα. Να υπολογίσετε :

γ. κατά πόσο τοις εκατό ελαττώθηκε η συχνότητα της ταλάντωσης μετά τη συσσωμάτωση και δ. το ελάχιστο μήκος του ελατηρίου κατά την ταλάντωση του συσσωματώματος

17. Ένα βάθρο εκτελεί με κατάλληλο μηχανισμό αρμονική ταλάντωση σε οριζόντια διεύθυνση με σταθερό πλάτος 0, 2 cm. Πάνω στο βάθρο βρίσκεται ένα αντικείμενο Σ και συμμετέχει στην ταλάντωση εφόσον η συχνότητα είναι σχετικά μικρή. Αν ο μηχανισμός μας επιτρέπει να κάνουμε διαδοχικά πειράματα με συχνότητα την οποία μπορούμε να αυξάνουμε - χωρίς να μεταβάλλουμε το πλάτος - σε ποια τιμή της συχνότητας το αντικείμενο Σ θα μετακινηθεί πάνω στο βάθρο; Δίνεται ο συντελεστής στατικής τριβής αντικειμένου Σ και βάθρου ίσος με 0,5.

18. Ένας δίσκος κρέμεται από το άκρο κατακόρυφου ελατηρίου και ενεργοποιούμενος εκτελεί αρμονική ταλάντωση συχνότητας 3 Hz. Το ίδιο σώμα, αν εξαρτηθεί από ένα άλλο κατακόρυφο ελατήριο Ε΄, εκτελεί απλή αρμονική ταλάντωση συχνότητας 4 Hz, Να υπολογίσετε τη συχνότητα ταλάντωσης του δίσκου αν εξαρτηθεί από τα άκρα και των δύο ελατηρίων, έτσι ώστε και τα δύο να είναι κατακόρυφα και ο δίσκος να παραμένει οριζόντιος

19. Ένα αντικείμενο μάζας 200 g εκτελεί αρμονική ταλάντωση συχνότητας 0,25 Hz και πλάτους 24 cm. Η απομάκρυνσή του κατά την αρχή των χρόνων είναι +24 cm.

Σας ζητούμε να προσδιορίσετε α. Τη θέση του κατά τη χρονική στιγμή 0,5 s. β. Τη συνισταμένη των ασκουμένων σε αυτό δυνάμεων κατά τη χρονική στιγμή 1 s . γ. Τον ελάχιστο χρόνο για να μετακινηθεί από την αρχική του θέση στη θέση με x = -12cm. δ. Τη δυναμική ενέργεια του ταλαντωτή κατά τη χρονική στιγμή 1,5 s.

ε. Τη μεταβολή της ορμής του από την χρονική στιγμή 2 s μέχρι τη χρονική στιγμή 3 s.

20. Το αντικείμενο Σ, μάζας 200 g, αφήνεται από ύψος 30 cm πάνω από τον δίσκο Δ, μάζας 800 g, ο οποίος είναι κρεμασμένος από ελατήριο σταθεράς 100 Ν/m . Αν η κρούση θεωρηθεί ελαστική να προσδιορίσετε

α. τη χαμηλότερη θέση στην οποία θα φθάσει ο δίσκος και τη θέση του αντικειμένου τη στιγμή εκείνη

β. την υψηλότερη θέση στην οποία θα φθάνει το αντικείμενο και την ταχύτητα του δίσκου κατά τη στιγμή εκείνη.

21. Όταν η σφαίρα ισορροπεί τα δύο ελατήρια είναι τεντωμένα και κατακόρυφα. Στη σφαίρα μεταβιβάζεται ενέργεια

30 J έτσι ώστε να εκτελέσει κατακόρυφη ταλάντωση. Να υπολογίσετε τη συχνότητα και το πλάτος της ταλάντωσης.

Δίνονται η μάζα της σφαίρας 1 kg, η σταθερά του πάνω ελατηρίου 300 N/m και η σταθερά του κάτω ελατηρίου 100 N/ m

22. Ένα ξύλινο αντικείμενο μάζας 100 g ακινητεί πάνω στη λεία επιφάνεια ενός τραπεζιού, δεμένο στη μία άκρη οριζόντιου ελατηρίου σταθεράς 300 N/m. Η άλλη άκρη του ελατηρίου είναι στερεωμένη σε ακίνητο στέλεχος, στο άκρο του τραπεζιού. Ένα βλήμα μάζας 20 g κινούμενο οριζόντια κατά τη διεύθυνση του άξονα του ελατηρίου, με ταχύτητα 30m/s, ενσφηνώνεται στο ξύλινο αντικείμενο και δημιουργείται ένα συσσωμάτωμα το οποίο εκτελεί αρμονική ταλάντωση. Αναφερόμενοι σε αυτό το συσσωμάτωμα σας ζητούμε να υπολογίσετε

α. την ταχύτητά του αμέσως μετά την ενσφήνωση

β. τη χρονική διάρκεια της κίνησής του από τη στιγμή της ενσφήνωσης μέχρι τη στιγμή που θα μηδενιστεί η ταχύτητά του για πρώτη φορά.

γ. το διάστημα που θα διανύσει μέχρι να σταματήσει στιγμιαία για πρώτη φορά

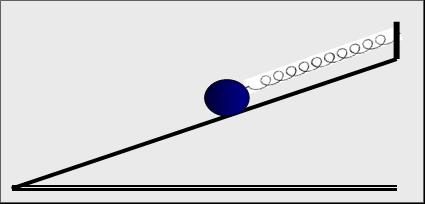
23. Το σώμα του σχήματος ισορροπεί και μπορεί να κινείται χωρίς τριβή. Το μετακινούμε προς τα κάτω κατά d έτσι ώστε να παραμείνει στο κεκλιμένο επίπεδο και το αφήνουμε ελεύθερο.

α. Na αποδείξετε ότι θα εκτελέσει απλή αρμονική ταλάντωση

β. Να προσδιορίσετε «πότε» θα ξαναβρεθεί στην αρχική του θέση για τρίτη φορά

γ. Να υπολογίσετε την κινητική του ενέργεια κάθε φορά που βρίσκεται στην αρχική του θέση.

Να θεωρήσετε γνωστά : τη σταθερά του ελατηρίου k, τη μάζα του m, την απόσταση d και το g.

24. Ένας αντικείμενο ισορροπεί στο άκρο κατακόρυφου ελατηρίου. Το μήκος του τεντωμένου ελατηρίου είναι 31 cm. Το αντικείμενο ενεργοποιείται με κατακόρυφη ταχύτητα προς τα πάνω και όταν φθάνει στο ανώτερο σημείο της τροχιάς το μήκος του ελατηρίου είναι 22 cm, ενώ την αμέσως επόμενη φορά, που το αντικείμενο ξαναβρίσκεται στο υψηλότερο σημείο της τροχιάς, το μήκος του ελατηρίου είναι 25 cm. Να προβλέψετε το μήκος του ελατηρίου όταν το αντικείμενο βρεθεί στο υψηλότερο σημείο τροχιάς του για τρίτη φορά. Να θεωρήσετε ότι κατά τη διάρκεια της ταλάντωσης στο αντικείμενο ασκείται δύναμη αντίστασης ανάλογη προς την ταχύτητά του .

25. Ένα βάθρο εκτελεί κατακόρυφη αρμονική ταλάντωση πλάτους Α cm έχοντας πάνω του ένα μικρό αντικείμενο. Εκτελούμε διαδοχικά πειράματα αυξάνοντας τη συχνότητα της ταλάντωσης και διατηρώντας το πλάτος σταθερό. Διαπιστώνεται ότι για συχνότητα ίση με 2 Hz το αντικείμενο αποχωρίζεται από το βάθρο. Σας ζητούμε να υπολογίσετε το σταθερό πλάτος της ταλάντωσης.

26. Ένα σώμα βρίσκεται σε οριζόντιο τραπέζι, με αμελητέα τριβή. Από τη μία πλευρά το σώμα συνδέεται με οριζόντιο ελατήριο σταθεράς k₁ = 150 N/m το άλλο άκρο του οποίου στερεώνεται σε κατακόρυφο τοίχωμα ενώ από την άλλη πλευρά το ίδιο σώμα συνδέεται με ένα άλλο οριζόντιο ελατήριο σταθεράς k₂ = 250 N/m το άλλο άκρο του οποίου στερεώνεται σε κατακόρυφο τοίχωμα απέναντι από το προηγούμενο. Το σώμα ενεργοποιείται με 2 τζάουλ έτσι ώστε να κινείται στο οριζόντιο τραπέζι και η μέγιστη τιμή της ταχύτητάς του να είναι 2 m/s.

α. Να αποδείξετε ότι το σώμα θα εκτελέσει απλή αρμονική ταλάντωση

β. Να υπολογίσετε τη μάζα του σώματος και το πλάτος της ταλάντωσης

Σε κάποια χρονική στιγμή κατά την οποία το σώμα διέρχεται από τη θέση ισορροπίας πέφτει πάνω του ένα κομμάτι λάσπη -κινούμενο μέχρι εκείνη τη στιγμή κατακόρυφα- μάζας 200 g που προσκολλάται σ΄ αυτό.

γ. Σας ζητούμε να υπολογίστε i. μετά πόσον χρόνο μετά την προσκόλληση το συσσωμάτωμα θα βρεθεί για πρώτη φορά στην ακραία θέση της ταλάντωσής του ii. το πλάτος της ταλάντωσης του συσσωματώματος

27. Ένας οριζόντιος δίσκος εκτελεί με κατάλληλο μηχανισμό κατακόρυφη αρμονική ταλάντωση με σταθερό πλάτος

0,2 m. Πάνω στο δίσκο βρίσκεται ένα αντικείμενο και συμμετέχει στην ταλάντωση εφόσον η συχνότητα είναι σχετικά μικρή. Αν ο μηχανισμός μας επιτρέπει να αυξήσουμε τη συχνότητα - χωρίς να μεταβάλλουμε το πλάτος - σε ποια τιμή της συχνότητας το αντικείμενο θα εγκαταλείψει τον δίσκο ;

Σχόλιο . Εφόσον το μάζας m αντικείμενο συμμετέχει στην αρμονική ταλάντωση ισχύει, σύμφωνα με τον νόμο του Νεύτωνα, ΣF = mα ΣF = - mω²x. Σε κάποια τυχαία στιγμή της κίνησης, πάνω από τη θέση ισορροπίας, ισχύει N - mg = - mω²x. Για να διατηρείται πάνω στον δίσκο πρέπει Ν > 0 .

28. Ένας οριζόντιος δίσκος μάζας 3m εκτελεί με κατάλληλο μηχανισμό κατακόρυφη αρμονική ταλάντωση συχνότητας 100/2π Hz και πλάτους 4cm με ελατήριο που βρίσκεται κάτω από αυτόν, η άλλη άκρη του οποίου είναι στερεωμένη στο έδαφος. Ένα αντικείμενο μάζας m πέφτει κατακόρυφα και συγκρούεται με το δίσκο κατά τη στιγμή που εκείνος βρισκόταν στη θέση ισορροπίας κινούμενος προς τα πάνω. Η ταχύτητα του αντικειμένου τη στιγμή πριν από τη σύγκρουση ήταν 4 m/s.

Να προβλέψετε α. πόσο ψηλά θα φθάσει το αντικείμενο μετά τη σύγκρουση

β. τι θα συμβεί στον δίσκο μετά τη σύγκρουση. Η κρούση να θεωρηθεί ελαστική.

Σχόλιο . Κατά την ελαστική κρούση διατηρείται τόσο η ορμή όσο και η ενέργεια του συστήματος. Χρειάζεται όμως προσοχή στο ζήτημα των αλγεβρικών τιμών των ταχυτήτων πριν και μετά την κρούση.

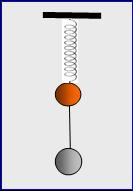
29. Στο άκρο κατακόρυφου ελατηρίου συνδέεται η σφαίρα Σ₁ μάζας 100 g και με κατακόρυφο τεντωμένο νήμα αμελητέας μάζας προσδένεται και η σφαίρα Σ₂ μάζας 300 g, όπως στο σχήμα. Το σύστημα ακινητεί έτσι ώστε το ελατήριο να είναι τεντωμένο κατά 4 cm σε σχέση με το φυσικό του μήκος. Το σύστημα στη συνέχεια ενεργοποιείται κατάλληλα εκτελεί κατακόρυφη αρμονική ταλάντωση πλάτους 12 cm .

α. Να υπολογίσετε τη σταθερά του ελατηρίου

β. Na υπολογίσετε τη σταθερά επαναφοράς της σφαίρας Σ₁.

γ. Να υπολογίσετε την τιμή της δύναμης του τεντωμένου νήματος τη στιγμή που η επιμήκυνση του ελατηρίου - σε σχέση με το φυσικό του μήκος - είναι 9 cm.

δ. Να προσδιορίσετε τη θέση στην οποία η τιμή της δύναμης του τεντωμένου νήματος είναι ελάχιστη.

30. Tο σώμα Σ μάζας 500g ακινητεί δεμένο στο άκρο κατακόρυφου ελατηρίου φυσικού μήκους 30 cm και σταθεράς 100Ν/m ενώ συγχρόνως συνδέεται και με τεντωμένο νήμα αμελητέας μάζας, η άλλη άκρη του οποίου προσδένεται στο έδαφος. Ενώ το σώμα ισορροπεί, το μήκος του ελατηρίου είναι 41 cm.

α. Να υπολογίσετε τη δύναμη που ασκεί το σώμα Σ στο τεντωμένο νήμα.

Σε κάποια χρονική στιγμή κόβουμε το νήμα και το σώμα εκτελεί αρμονική ταλάντωση

β. Να υπολογίσετε i. σε πόσο χρονικό διάστημα το Σ θα μετακινηθεί από την κατώτερη στην ανώτερη θέση

ii . το μικρότερο μήκος που θα έχει το ελατήριο κατά τη διάρκεια της κίνησης

iii . τη μέγιστη κινητική ενέργεια που θα αποκτήσει το σώμα

iv. το μήκος του ελατηρίου τη στιγμή που η ταχύτητα του Σ θα έχει μέτρο 20√10 cm/s ( δύο λύσεις )

"

31. Ένας οριζόντιος δίσκος μάζας Μ είναι στερεωμένος στο άνω άκρο ελατηρίου σταθεράς k, το άλλο άκρο του οποίου στερεώνεται σε οριζόντιο έδαφος. Πάνω στο δίσκο βρίσκεται ακίνητο κουνούπι μάζας m, το οποίο σε κάποια στιγμή πετάει προς τα πάνω με ταχύτητα υ. Ζητείται το πλάτος της ταλάντωσης του δίσκου. Δίνονται τα m, M, k, υ και g

32. Κατά την ευθύγραμμη κίνηση ενός υλικού σημείου η χρονική συνάρτηση της θέσης (απομάκρυνσης) είναι

x = 12συν8πt + 12 ημ(8πt-π/6) ( οι τιμές του x σε cm και του t σε s )

α. Να αποδείξετε ότι η κίνηση είναι αρμονική ταλάντωση.

β. Με δεδομένο ότι η μάζα του υλικού σημείου είναι 300 g να προσδιορίσετε

i. τη σταθερά επαναφοράς της ταλάντωσής του

ii. τη θέση του κατά την αρχή των χρόνων

iii. τη χρονική στιγμή που θα βρεθεί για πρώτη φορά στη θέση ισορροπίας

iv. την επιτάχυνσή του κατά τη χρονική στιγμή 1 s.

v. την κινητική του ενέργεια κάθε φορά που απέχει 6 cm από τη θέση ισορροπίας.

33. Ένα υλικό σημείο συμμετέχει σε δύο αρμονικές ταλαντώσεις της ίδιας διεύθυνσης και με την ίδια θέση ισορροπίας.

Οι εξισώσεις για κάθε κίνηση είναι αντίστοιχα

x₁ = 0,06ημ(30t +π/2) και x₂ = 0,06ημ(30t + 7π/6).

Σας ζητούμε α. να υπολογίσετε το πλάτος και τη συχνότητα της κίνησης και

β. να γράψετε την εξίσωση της κίνησης.

34. Ένα υλικό σημείο συμμετέχει σε δύο αρμονικές ταλαντώσεις - την 1 και την 2 - της ίδιας διεύθυνσης και με την ίδια θέση ισορροπίας. Οι εξισώσεις για κάθε κίνηση είναι αντίστοιχα x₁ = 0,08ημ(7πt + π/6) και x₂ = 0,06ημ(7πt + 4π/6).

Σας ζητούμε να υπολογίσετε το πλάτος και τη συχνότητα της σύνθετης ταλάντωσης και τη διαφορά φάσης της

της σύνθετης ταλάντωσης από την ταλάντωση 2.

35. Ένα υλικό σημείο συμμετέχει σε δύο αρμονικές ταλαντώσεις - την 1 και την 2 - της ίδιας διεύθυνσης με ίσες συχνότητες και με την ίδια θέση ισορροπίας. Η εξίσωση για την ταλάντωση 1 είναι x₁ = 0,1ημ(4πt +11π/12)

ενώ η εξίσωση της σύνθετης ταλάντωσης είναι x = 0,1ημ(4πt + 7π/12). Να γράψετε την εξίσωση της ταλάντωσης 2 .

36. Ένα υλικό σημείο συμμετέχει ταυτόχρονα σε δύο ταλαντώσεις με την ίδια θέση ισορροπίας οι οποίες περιγράφονται από τις σχέσεις x₁= 3ημ50t και x₂= 3ημ52t. ( οι τιμές του x σε cm και του t σε s ) Η σύνθετη ταλάντωσή του θα έχει :

α. συχνότητα 4 Hz β. συχνότητα 102 Hz

γ. πλάτος που μεταβάλλεται μεταξύ των τιμών μηδέν και 6 cm.

δ .πλάτος που μεταβάλλεται μεταξύ των τιμών μηδέν και 3 cm.

37. Ένα υλικό σημείο συμμετέχει σε δύο αρμονικές ταλαντώσεις της ίδιας διεύθυνσης τα πλάτη των οποίων είναι ίσα. Διαπιστώνεται ότι ανά χρονικά διαστήματα ίσα με 0,5 s το πλάτος της σύνθετης κίνησης μηδενίζεται. Να υπολογίσετε τη συχνότητα της ταλάντωσης με τη μικρότερη συχνότητα, με δεδομένο ότι η συχνότητα της άλλης ταλάντωσης είναι 230 Hz .

38. Σε ένα ηλεκτρικό κύκλωμα που εκτελεί αμείωτη ηλεκτρική ταλάντωση διαπιστώνεται ότι η περίοδος

είναι 4.10^-3 s. Εάν οκταπλασιάσουμε τον συντελεστή αυτεπαγωγής και υποδιπλασιάσουμε

τη χωρητικότητα του πυκνωτή ποια θα είναι η νέα τιμή της συχνότητας; Να δικαιολογήσετε την απάντηση

39. Ένα κύκλωμα αμείωτης ηλεκτρικής ταλάντωσης αποτελείται από πυκνωτή 5μ F και πηνίο 2 mH . Φέρνουμε τους οπλισμούς του πυκνωτή σε στιγμιαία επαφή με τους πόλους μιας πηγής τάσης 20 βολτ. Να υπολογίσετε α. τη μέγιστη τιμή της ενέργειας της αποθηκευμένης στο μαγνητικό πεδίο του πηνίου. β. Το μικρότερο χρονικό διάστημα ανάμεσα σε δύο στιγμές κατά τις οποίες η ενέργεια η αποθηκευμένη στο μαγνητικό πεδίο του πηνίου αποκτά τη μέγιστη τιμή της. γ. Την μέγιστη τιμή της έντασης του εναλλασσόμενου ρεύματος δ. Την ελάχιστη χρονική διάρκεια ανάμεσα στη στιγμή που έγινε η φόρτιση του πυκνωτή – κατά τη σύνδεσή του με τους πόλους της πηγής – και στη στιγμή κατά την οποία η ενέργεια η αποθηκευμένη στο ηλεκτρικό πεδίο έχει μειωθεί στο μισό.

40. Κατά τη διάρκεια μιας αμείωτης ηλεκτρομαγνητικής ταλάντωσης συχνότητας 5 kHz η ενέργεια του κυκλώματος είναι 10^-5 J. Το πηνίο έχει συντελεστή αυτεπαγωγής 1mΗ. Να υπολογίσετε

α. το πλάτος του ρεύματος β. την τιμή του ρεύματος κατά τη στιγμή που η ενέργεια του ηλεκτρικού πεδίου

είναι 6.10^-6 J. γ. τη χωρητικότητα του πυκνωτή

41. H αμείωτη ηλεκτρική ταλάντωση ενός κυκλώματος με πυκνωτή χωρητικότητας 5.10^-6 F περιγράφεται με την εξίσωση

q = 2.10^-6ημ2000πt. Να υπολογίσετε α. την τιμή του συντελεστή αυτεπαγωγής. β. την ενέργεια του μαγνητικού πεδίου του πηνίου τη χρονική στιγμή 7,5.10^-3 s. γ. το ηλεκτρικό φορτίο του πυκνωτή τη στιγμή

42. H αμείωτη ηλεκτρική ταλάντωση ενός κυκλώματος με πηνίο συντελεστή 40 mH περιγράφεται με την εξίσωση

i = - 12.10^-3ημ600πt. Να υπολογίσετε α. το μέγιστο φορτίο του πυκνωτή β. τη χωρητικότητα του πυκνωτή

γ. την ενέργεια του ηλεκτρικού πεδίου του πυκνωτή τη στιγμή που η ένταση του ρεύματος είναι 10 mA .

δ. την ένταση του ρεύματος τη στιγμή που το φορτίο του πυκνωτή είναι π μC.

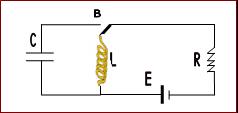
43. Αρχικά ο μεταγωγός βρίσκεται στη θέση του σχήματος. Σε κάποια στιγμή μετακινείται στη θέση Β και στο κύκλωμα με τον πυκνωτή και το πηνίο δημιουργείται αμείωτη ηλεκτρική ταλάντωση. α. Να γράψετε τη συνάρτηση ρεύματος χρόνου θεωρώντας ως Αρχή των χρόνων τη στιγμή που μετακινήθηκε ο μεταγωγός. β. Να προσδιορίσετε τη φορά του και την τιμή του ρεύματος κατά τη χρονική στιγμή 9Τ/8, όπου Τ η περίοδος της ταλάντωσης . γ. Να υπολογίσετε την ενέργεια του μαγνητικού πεδίου του πηνίου τη στιγμή που το ηλεκτρικό φορτίο του πυκνωτή είναι 120 μC .

Δίνονται C = 18.10^-6 F L = 20 mH R = 100 Ω Ε = 40 V.

44. Κατά την εξέλιξη μιας φθίνουσας ηλεκτρικής ταλάντωσης η ενέργεια υποβαθμίζεται λόγω της παρουσίας του

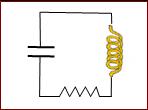
αντιστάτη. Τη χρονική στιγμή t = 0 η ένταση του ρεύματος στο κύκλωμα έχε τη μέγιστη τιμή ίση με 216 mA, τη χρονική στιγμή t = t_a έχει και πάλι τη μέγιστη τιμή ίση με 180 mA, ενώ τη χρονική στιγμή t = 2t_a η ενέργεια του μαγνητικού πεδίου του πηνίου είναι 22,5.10^-6 J. Να υπολογίσετε την τιμή του συντελεστή αυτεπαγωγής του πηνίου.

45. Στο ιδανικό κύκλωμα του σχήματος έχουμε αρχικά τους διακόπτες Δ₁ και Δ₂ ανοικτούς

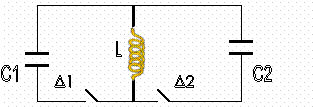
Ο πυκνωτής χωρητικότητας C₁ έχει φορτιστεί μέσω πηγής συνεχούς τάσης με φορτίο Q₁. Τη χρονική στιγμή t₀ = 0 ο διακόπτης Δ₁ κλείνει, οπότε το κύκλωμα LC₁ εκτελεί αμείωτη ηλεκτρική ταλάντωση. Τη χρονική στιγμή t₁ = 5T/4, όπου Τ η περίοδος της ταλάντωσης του κυκλώματος LC₁, ο διακόπτης Δ₁ ανοίγει και ταυτόχρονα κλείνει ο Δ₂. Το μέγιστο φορτίο Q₂ που θα αποκτήσει ο πυκνωτής χωρητικότητας C₂ όπου C₂ = 4C₁ , κατά τη διάρκεια της ηλεκτρικής ταλάντωσης του κυκλώματος LC₂ , θα είναι ίσο με α. Q₁ β. ½ Q₁ γ. 2Q₁ Να αιτιολογήσετε την απάντησή σας