Ανδρέας Ιωάννου Κασσέτας

( Στις σχετικές συναρτήσεις , εφόσον δεν αναφέρεται κάτι διαφορετικό, οι τιμές των x, y και t είναι στο S.I. ‘Όταν αναφέρεται ότι «δύο υλικά σημεία του ελαστικού μέσου απέχουν x cm» υποδηλώνεται ότι |x cm απέχουν οι θέσεις ισορροπίας των δύο αυτών ταλαντωτών» )

1. Η εξίσωση ενός αρμονικού κύματος στο οποίο διαδίδεται σε γραμμικό ελαστικό μέσο είναι y = 0, 04ημπ( 2t – 5x) .

Σας ζητούμε α. να υπολογίσετε την ταχύτητα διάδοσης του κύματος

β. να προσδιορίσετε την επιτάχυνση της ταλάντωσης ενός υλικού σημείου που απέχει από την πηγή 2cm κατά τη χρονική στιγμή 1s. γ. να υπολογίσετε την απόσταση των δύο πλησιέστερων υλικών σημείων του μέσου τα οποία έχουν συνεχώς διαφορά φάσης π/8

2. Ένας αρμονικός ταλαντωτής Σ ταλαντώνεται με περίοδο 0,2 s και πλάτος Α έτσι ώστε η μέγιστη ταχύτητα της ταλάντωσης να είναι π m/s και δημιουργεί κύμα σε ορισμένο γραμμικό ελαστικό μέσο. Διαπιστώνεται ότι τα μεταξύ τους πλησιέστερα υλικά σημεία τα οποία βρίσκονται συνεχώς σε συμφωνία φάσης, απέχουν ( οι θέσεις ισορροπίας τους ) 5 cm.

Na γράψετε την εξίσωση του αρμονικού κύματος, βασιζόμενοι στο ότι η εξίσωση της κίνησης του Σ είναι y = Aημ10πt.

3. Η κίνηση ενός αρμονικού ταλαντωτή Π περιγράφεται με τη συνάρτηση y = 0,05ημ5πt. Ο Π αποτελεί πηγή αρμονικού κύματος το οποίο διαδίδεται σε γραμμικό ελαστικό μέσο. Διαπιστώνεται ότι κατά τη χρονική στιγμή 0,3 s, η απομάκρυνση ενός υλικού σημείου Σ, η θέση ισορροπίας του οποίου απέχει 8 cm από την αντίστοιχη του Π, είναι +2,5 cm. Και άλλα υλικά σημεία κατά τη χρονική εκείνη στιγμή έχουν την ίδια απομάκρυνση με το Σ αλλά το Σ είναι πλησιέστερο στον ταλαντωτή Π . Na υπολογίσετε το μήκος κύματος και την ταχύτητα διάδοσης του κύματος

4. Ένα εγκάρσιο κύμα διαδίδεται σε γραμμικό ελαστικό μέσο .

Θεωρούμε αρχή των αξόνων ένα σημείο στο οποίο βρίσκεται το υλικό σημείο Ο του μέσου ελαστικού μέσου. Θεωρούμε αρχή των χρόνων μία χρονική στιγμή κατά την οποία ενεργοποιείται το υλικό σημείο Ο, έτσι ώστε να βρίσκεται στη θέση ισορροπίας κινούμενο προς τον θετικό ημιάξονα

Με δεδομένα ότι (i) τη χρονική στιγμή t = 1s το σημείο Β με συντεταγμένη x_Β = 1,5m διέρχεται από τη θέση ισορροπίας με κατεύθυνση προς τα αρνητικά για δεύτερη φορά στη διάρκεια του 1s.

(ii) τη χρονική στιγμή 3s το σημείο Γ με x_Γ = 1 m έχει φάση 18π.

α . Να υπολογίσετε τη συχνότητα και το μήκος κύματος.

β. Να υπολογίσετε τη διαφορά φάσης φ_Γ – φ_Β των κινήσεων των υλικών σημείων Γ και Β .

γ. Να κάνετε , σε κοινό διάγραμμα, τη γραφική παράσταση της χρονικής εξέλιξης της φάσης του Β και της φάσης του Γ .

5. Δύο σύγχρονες πηγές ταλαντούμενες με πλάτος 4 cm και συχνότητα 25 Hz δημιουργούν εγκάρσια κύματα κάθετα στην επιφάνεια ενός υγρού όπου η ταχύτητα διάδοσης είναι 150 cm/s.

α. Να περιγράψετε την κίνηση ενός υλικού σημείων του μέσου το οποίο απέχει 17 cm από τη μία πηγή και 29 cm από την άλλη β. Να προσδιορίσετε το σύνολο των υλικών σημείων του μέσου τα οποία παραμένουν ακίνητα.

6. Δύο σύγχρονες πηγές ταλαντούμενες με πλάτος 4 cm και συχνότητα 50 Hz δημιουργούν εγκάρσια κύματα κάθετα στην επιφάνεια ενός υγρού όπου η ταχύτητα διάδοσης είναι 2 m/s. α. Να περιγράψετε την κίνηση ενός υλικού σημείων του μέσου το οποίο απέχει 12 cm από τη μία πηγή και 13 cm από την άλλη

β. Να προσδιορίσετε το σύνολο των υλικών σημείων του μέσου που εκτελούν αρμονική ταλάντωση με πλάτος 4 cm

7. Δύο σύγχρονες πηγές - Π₁ και Π₂ - κυμάτων απέχουν 24 cm. Τα δημιουργούμενα εγκάρσια επιφανειακά κύματα

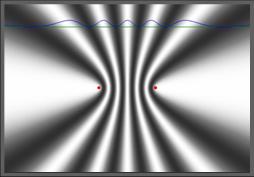
έχουν συχνότητες 100 Hz και διαδιδόμενα στο ίδιο ελαστικό μέσο με ταχύτητες 6 m/s συμβάλλουν. Διαπιστώνεται ότι τα υλικά σημεία του μέσου που βρίσκονται στη μεσοκάθετο της Π₁Π₂ δημιουργείται ενίσχυση των κυμάτων. Να προσδιορίσετε το πλήθος των υπερβολών απόσβεσης .

8. Δύο εγκάρσια επιφανειακά κύματα προερχόμενα από πηγές συχνοτήτων 120 Hz και διαδιδόμενα στο ίδιο ελαστικό μέσο με ταχύτητες 12 m/s συμβάλλουν. Αν η εξίσωση για τη μία πηγή Π₁ είναι y₁= Aημωt και για τη άλλη πηγή Π₂ y₂ = Aημ(ωt+π) διαπιστώνεται ότι ορισμένα υλικά σημεία του μέσου διατηρούνται ακίνητα. Βασιζόμενοι στην εξίσωση αρμονικού κύματος και στην αρχή της επαλληλίας να προσδιορίσετε το σύνολο των ακίνητων αυτών υλικών σημείων.

9. Δύο εγκάρσια επιφανειακά κύματα προερχόμενα από πηγές ίσων συχνοτήτων και διαδιδόμενα στο ίδιο ελαστικό μέσο με ταχύτητες 4 m/s συμβάλλουν. Αν η εξίσωση για τη μία πηγή είναι y₁ = 3ημ200πt και για τη άλλη πηγή y₂ = 3ημ( 200πt+π) – το x σε cm, το t σε s – σας ζητούμε α. να υπολογίσετε το μήκος κύματος καθενός από τα δύο κύματα β. να προσδιορίσετε την εξίσωση κίνησης ενός υλικού σημείου που απέχει x₁ = 16 cm x₂ = 10 cm αντίστοιχα από κάθε πηγή

10. Δύο σύγχρονες πηγές ταλαντούμενες με πλάτος 20 mm και συχνότητα 50 Hz δημιουργούν εγκάρσια κύματα κάθετα στην επιφάνεια ενός υγρού όπου η ταχύτητα διάδοσης είναι 3 m/s. Να προσδιορίσετε το πλάτος της ταλάντωσης ενός υλικού σημείου του ελαστικού μέσου στις περιπτώσεις που αυτό απέχει α. 22 cm από τη μία πηγή και 30 cm από την άλλη β. 14 cm από τη μία πηγή και 20 cm από την άλλη γ. 17cm από τη μία πηγή και 9 cm από την άλλη

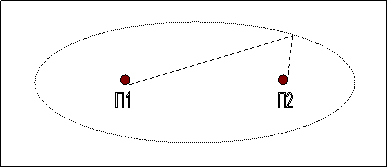
11. Δύο σύγχρονες πηγές - Π₁ και Π₂ – συχνοτήτων 100 Hz δημιουργούν εγκάρσια επιφανειακά κύματα διαδιδόμενα στο ίδιο ελαστικό μέσο με ταχύτητες 4 m/s, τα οποία συμβάλλουν. Να αποδείξετε ότι όλα τα κινούμενα υλικά σημεία της επιφάνειας των οποίων το άθροισμα των αποστάσεων από τις Π₁ και Π₂ είναι 24cm εκτελούν ταλαντώσεις της ίδιας φάσης με τις δύο πηγές. Ο γεωμετρικός τόπος αυτών των σημείων είναι μια έλλειψη.

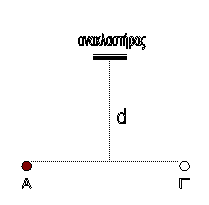
13. Η πηγή Α εκτελεί ταλάντωση y = 3ημ20πt - το y σε cm - και δημιουργεί εγκάρσια επιφανειακά κύματα στην επιφάνεια υγρού τα οποία διαδίδονται με ταχύτητα 4 m/s. α. Να γράψετε την εξίσωση της ταλάντωσης ενός υλικού σημείου της επιφάνειας το οποίο απέχει από την πηγή Α β. Θεωρούμε το ευθύγραμμο τμήμα ΑΓ = 80 cm όπως στο σχήμα. Αν τοποθετήσουμε ένα ανακλαστήρα ασήμαντων διαστάσεων στην περιοχή της μεσοκαθέτου στην ΑΓ και παράλληλα προς την ΑΓ , το κύμα ανακλώμενο στο σημείο Ζ ( σχήμα ) συμβάλλει με το κύμα που εκπορεύεται απευθείας από την πηγή. Τοποθετώντας τον ανακλαστήρα σε κατάλληλη απόσταση d διαπιστώνουμε ότι - λόγω της συμβολής των κυμάτων - το υλικό σημείο που βρίσκεται στη θέση Γ διατηρείται συνεχώς ακίνητο.

Να προσδιορίσετε την ελάχιστη απόσταση d.

14. Δύο κύματα με ίσες συχνότητες και πλάτος 20 mm διαδιδόμενα στο ίδιο ελαστικό μέσο με ταχύτητες 40cm/s συμβάλλουν και δημιουργούν στάσιμο κύμα. Η απόσταση ενός δεσμού από την επόμενη κοιλία είναι 2,5 cm. Na προσδιορίσετε

α. τη συχνότητα κάθε κύματος β. το πλάτος ταλάντωσης κάθε κοιλίας

γ. την απόσταση από μία κοιλία του πλησιέστερου σε αυτήν υλικού σημείου που εκτελεί ταλάντωση πλάτους 2 mm.

15. Ένα κύμα με εξίσωση y = 0, 04ημ2π( 8t- 2x) διαδίδεται σε κάποιο ελαστικό μέσον. Στο ίδιο μέσον, με αντίθετη κατεύθυνση, διαδίδεται ένα απολύτως παρόμοιο κύμα. Ποια είναι η ταχύτητα κάθε κύματος πριν αυτά συμβάλουν; Μετά τη συμβολή των δύο κυμάτων, κάθε υλικό σημείο του μέσου - πλην ορισμένων- εκτελεί αρμονική ταλάντωση. Κατά τη χρονική στιγμή t= 1,1 s να προσδιορίσετε τις θέσεις των υλικών σημείων του μέσου με x₁ = 25 cm και x₂ = 1/12 m. Να διερευνήσετε εάν είναι ορθή ή λανθασμένη η εκτίμηση ότι ένα σημείο με

x₃ = 12, 5 cm αποτελεί κοιλία.

16. Στο σχήμα απεικονίζεται το στιγμιότυπο ενός στάσιμου κύματος που έχει προκύψει από τη συμβολή δύο ομοίων

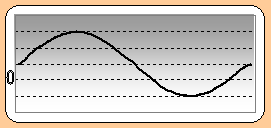
κυμάτων καθένα από τα οποία έχει συχνότητα 20 Hz και διαδίδεται με ταχύτητα 4m/s.

Στο στιγμιότυπο κάθε υλικό σημείο έχει μηδενική ταχύτητα και στο σημείο 0 βρίσκεται δεσμός.

α. να υπολογίσετε την απόσταση δύο διαδοχικών δεσμών

β. Να σχεδιάσετε από κάτω το στιγμιότυπο του στάσιμου αυτού κύματος μετά από 1/40 s.

17. Στο σχήμα απεικονίζεται το στιγμιότυπο ενός (τρέχοντος) κύματος το οποίο διαδίδεται προς τα δεξιά με ταχύτητα 6m/s και συχνότητα 10 Hz. Να σχεδιάσετε από κάτω το στιγμιότυπο του ίδιου αυτού κύματος μετά από 1/40 s.

( Στο σημείο 0 βρίσκεται υλικό σημείο με x = 0 )

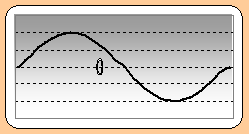
18. Ένα κύμα με εξίσωση y = 0,1ημ2π(4t - 10x) διαδίδεται σε κάποιο γραμμικό ελαστικό μέσον. Στο ίδιο μέσον, με αντίθετη κατεύθυνση, διαδίδεται ένα απολύτως όμοιο κύμα. Με τη συμβολή των δύο κυμάτων δημιουργείται στάσιμο κύμα. Να προσδιορίσετε α. τη μικρότερη απόσταση δύο διαδοχικών δεσμών.

β. Το πλάτος ταλάντωσης ενός υλικού σημείου Ρ που απέχει – η θέση ισορροπίας του – 5/ 3 cm από μία κοιλία

19. Ένα στάσιμο κύμα προκύπτει από τη συμβολή δύο όμοιων κυμάτων συχνοτήτων 8 Hz που διαδίδονται στο ίδιο ελαστικό μέσο με αντίθετες κατευθύνσεις και με ταχύτητες 64 cm/s. Εάν το πλάτος ταλάντωσης κάθε κοιλίας είναι 6 cm να προσδιορίσετε την επιτάχυνση ενός υλικού σημείου Ρ το οποίο – η θέση ισορροπίας του - απέχει από μία κοιλία 1cm σε μία χρονική στιγμή κατά την οποία η κάθε κοιλία βρίσκεται στη μέγιστη απομάκρυνση.

20. Κατά μήκος του άξονα x΄x εκτείνεται ελαστική χορδή. Στη χορδή διαδίδεται εγκάρσιο αρμονικό κύμα. Η εγκάρσια απομάκρυνση ενός σημείου Π₁ της χορδής περιγράφεται με την εξίσωση y₁= Αημ30πt (SI) ενώ η εγκάρσια απομάκρυνση ενός σημείου Π₂, που βρίσκεται 6cm δεξιά του σημείου Π₁, περιγράφεται με την εξίσωση: y₁= Α (ημ30πt + π/6 ) (SI) . Η απόσταση μεταξύ των σημείων Π₁ και Π₂ είναι μικρότερη από ένα μήκος κύματος

α. Ποια είναι η φορά διάδοσης του κύματος;

β. Ποια είναι η ταχύτητα διάδοσης του κύματος;

γ. Αν η ταχύτητα διάδοσης του κύματος είναι ίση με τη μέγιστη ταχύτητα ταλάντωσης των σημείων της χορδής να υπολογίσετε το πλάτος του κύματος

21. Στο σχήμα που ακολουθεί, απεικονίζεται ένα στιγμιότυπο κύματος. Εκείνη τη στιγμή σε ποια από τα σημεία Α, Β, Γ,

Δ, Ε, Ζ και Η, η ταχύτητα ταλάντωσης είναι μηδενική ; Ποια είναι η φορά της ταχύτητας της ταλάντωσης των σημείων Β, Δ, και Ζ;

22. Ένα τεντωμένο οριζόντιο σκοινί ΟΑ μήκους L εκτείνεται κατά τη διεύθυνση του άξονα x . Το άκρο του Α είναι στερεωμένο ακλόνητα στη θέση x = L , ενώ το άκρο Ο που βρίσκεται στη θέση x = 0 είναι ελεύθερο, έτσι ώστε με κατάλληλη διαδικασία να δημιουργείται στάσιμο κύμα με 3 συνολικά κοιλίες. Στη θέση x = 0 εμφανίζεται κοιλία και το υλικό σημείο του σκοινιού στη θέση αυτή εκτελεί απλή αρμονική ταλάντωση . Τη χρονική στιγμή t = 0 το σημείο Ο

( x = 0 ) βρίσκεται στη θέση μηδενικής απομάκρυνσης κινούμενο κατά τη θετική φορά. Η απόσταση των ακραίων θέσεων της ταλάντωσης αυτού του υλικού αυτού σημείου Ο είναι 0,2 m. Το συγκεκριμένο σημείο Ο διέρχεται από τη θέση ισορροπίας του 4 φορές κάθε δευτερόλεπτο και απέχει, κατά τον άξονα x , 0, 1 m από τον πλησιέστερο δεσμό

α. Να υπολογίσετε τη συχνότητα του κύματος.

β. Να υπολογίσετε το μήκος L του σκοινιού

γ. Να υπολογίσετε το μέτρο της ταχύτητας της ταλάντωσης του υλικού σημείου με x = 0 κατά τη χρονική στιγμή που η απομάκρυνσή του από τη θέση ισορροπίας είναι y = + 5 cm

δ. Να γράψετε την εξίσωση του στάσιμου κύματος θεωρώντας ως αρχή των αξόνων το άκρο Ο

ε. Να γράψετε την εξίσωση του στάσιμου κύματος θεωρώντας ως αρχή των αξόνων τον πλησιέστερο προς το άκρο Ο δεσμό.