Ανδρέας Ιωάννου Κασσέτας

Σε όλες τις περιπτώσεις η ταχύτητα διάδοσης στο κενό να θεωρηθεί ίση 3.10⁸m/s².

1. Ποια από τα παρακάτω ζεύγη εξισώσεων μπορεί να αναφέρεται σε ηλεκτρομαγνητικό κύμα διαδιδόμενο στο κενό; Να δικαιολογήσετε κάθε απάντηση

α. Ε = 120ημ2π(10⁸t – 0,4x) και Β = 4.10^-7ημ2π (10⁸t – 0,4x)

β. Ε = 120ημ2π(10⁸t – x/3) και Β = 4.10^-7ημ2π(10⁸t – x/3)

γ. Ε = 30ημ(10⁸t – x/3) και Β = 10^-7ημ(10⁸t – x/3)

δ. Ε = 90ημ2π(6.10⁸t – 2x) και Β = 3.10^-7ημ2π(10⁸t – x/3)

2. Ένα ηλεκτρομαγνητικό κύμα, αναφερόμενο σε πορτοκαλί ακτινοβολία διαδιδόμενη στο κενό, περιγράφεται με τις εξισώσεις

Ε = 90ημ2π(5.10¹⁴t – 10⁷x/6) και Β = 3.10^-7ημ2π(5.10¹⁴t – 10⁷x/6)

α. Να αποδείξετε ότι το κύμα διαδίδεται στο κενό. β. Να καταγράψετε τις αντίστοιχες εξισώσεις κατά τη διάδοσή του κύματος σε νερό - δείκτη διάθλασης 4/3 - με δεδομένο ότι στο νερό η μέγιστη τιμή της έντασης του ηλεκτρικού πεδίου είναι ελαττωμένη κατά 20% σε σχέση με εκείνη που παρουσιάζει στο κενό.

3. Ένα ηλεκτρομαγνητικό κύμα, αναφερόμενο σε πράσινη ακτινοβολία διαδιδόμενη σε γυαλί, περιγράφεται με τις εξισώσεις

Ε = 20ημ2π(ft – 10⁷x/6) και Β = 10^-7ημ2π(ft – 10⁷x/6)

Εάν είναι γνωστό ότι στο γυαλί η μέγιστη τιμή της έντασης του ηλεκτρικού πεδίου είναι ελαττωμένη κατά 20% σε σχέση με εκείνη του κενού. α. Να καταγράψετε τις αντίστοιχες εξισώσεις κατά τη διάδοσή στο κενό

β. Να υπολογίσετε τον δείκτη διάθλασης του γυαλιού.

4. Ένα ηλεκτρομαγνητικό κύμα, περιγράφεται με τις εξισώσεις

Ε = 30ημ2π(5.10¹⁵t – x/λ) και Β = 10^-7ημ2π(5.10¹⁵t – x/λ) Να αποφανθείτε

α. εάν διαδίδεται στο κενό β. εάν πρόκειται για υπέρυθρη, για ορατή ή για υπεριώδη ακτινοβολία εφόσον δεχόμαστε ότι για το μήκος κύματος λ των ορατών ακτινοβολιών ισχύει 400 nm < λ < 700 nm

5. Κατά την περιγραφή ενός ηλεκτρομαγνητικού κύματος διαδιδόμενου στο κενό η εξίσωση της ταλάντωσης του άκρου της έντασης Ε σε ένα σημείο 0 που θεωρείται αρχή των αξόνων είναι Ε = 90ημ2π.10⁸t.

Να προσδιορίσετε την τιμή της έντασης Β ενός σημείου που απέχει 2,25 m από το 0 - στην κατεύθυνση διάδοσης- τη χρονική στιγμή 10^-8 s

6. Ένα ραδιόφωνο είναι συντονισμένο σε σταθμό 100 ΜΗz. Η χωρητικότητα του πυκνωτή επιλογής του ραδιοφώνου κατά τον συντονισμό είναι 2,5.10^-14 F. Το πλάτος της έντασης του ηλεκτρικού πεδίου στην περιοχή που βρίσκεται το ραδιόφωνο είναι 90 V/m.

a. Να υπολογίσετε την τιμή του συντελεστή αυτεπαγωγής του κυκλώματος επιλογής του ραδιοφώνου

β. Να γράψετε τις εξισώσεις που περιγράφουν το ηλεκτρομαγνητικό κύμα του σταθμού, θεωρώντας αρχή αξόνων ένα σημείο 0 στο οποίο Ε = Ε_maxημωt

7. Το κύκλωμα ηλεκτρικής ταλάντωσης ενός ραδιοφωνικού σταθμού αποτελείται από πηνίο με συντελεστή αυτεπαγωγής 2μ Η και πυκνωτή η χωρητικότητα του οποίου κατά την εκπομπή του ραδιοκύματος είναι 2 pF Σε κάποια απόσταση από την κεραία βρίσκεται μία μεταλλική επιφάνεια τοποθετημένη κάθετα στη διεύθυνση διάδοσης του ραδιοκύματος οπότε το εκπεμπόμενο κύμα ανακλάται με συνέπεια να δημιουργείται στάσιμο κύμα. Να προσδιορίσετε την απόσταση δύο διαδοχικών δεσμών του στάσιμου κύματος

8. Ένα ηλεκτρομαγνητικό κύμα συχνότητας 3.10⁸ Hz προσπίπτει στο νερό υπό γωνία πρόσπτωσης 45⁰ , κατευθυνόμενο προς ένα υποβρύχιο. Εάν το πλάτος της έντασης του ηλεκτρικού πεδίου μέσα στο νερό είναι 60 V/m και η γωνία διάθλασης 30⁰ να καταγράψετε τις συναρτήσεις Ε = Ε ( x, t ) και

Β = Β ( x, t ) που περιγράφουν τη διάδοση του ηλεκτρομαγνητικού πεδίου μέσα στο νερό.

9. Ένα ηλεκτρομαγνητικό κύμα, περιγράφεται με τις εξισώσεις

Ε = 30ημ2π(5.10¹⁵t – x/λ) και Β = 10^-7ημ2π(5.10¹⁵t – x/λ) Να αποφανθείτε

α. εάν διαδίδεται στο κενό β. εάν πρόκειται για υπέρυθρη, για ορατή ή για υπεριώδη ακτινοβολία αποδεχόμενοι ότι για το μήκος κύματος λ των ορατών ακτινοβολιών ισχύει 400.10^-9m < λ < 700.10^-9m. Να δικαιολογήσετε τις απαντήσεις σας

1. Εάν είναι γνωστό ότι οι δείκτες διάθλασης ενός ορισμένου τύπου γυαλιού για την ερυθρή και για την ιώδη ακτινοβολία είναι αντίστοιχα 1,51 και 1,53 και ότι το μήκος κύματος στο κενό της ερυθράς είναι 700 nm και της ιώδους 400 nm να υπολογίσετε

α. την ταχύτητα του φωτός για την ερυθρά και την ιώδη ακτινοβολία στο γυαλί. β. τη συχνότητα της ερυθράς και της ιώδους

γ. Το μήκος κύματος καθεμιάς στο γυαλί.

2. Στη μία έδρα πρίσματος διαθλαστικής γωνίας 60⁰ προσπίπτει φωτεινή μονοχρωματική ακτίνα υπό γωνία προσπτώσεως 60⁰. Να υπολογίσετε την εκτροπή της, τη γωνία δηλαδή μεταξύ της αρχικά προσπίπτουσας στο πρίσμα και της τελικώς εξερχόμενης από αυτό, εάν είναι γνωστό ότι ο δείκτης διάθλασης είναι √3.

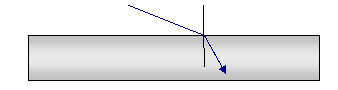
3. Μια φωτεινή ακτίνα προερχόμενη από τον αέρα προσπίπτει σε μία διαφανή πλάκα με παράλληλες έδρες, διαθλώμενη εισέρχεται στο εσωτερικό της και προσπίπτει σε σημείο της εσωτερικής επιφάνειας . Να αποδείξετε ότι είναι αδύνατον να συμβεί ολική ανάκλαση

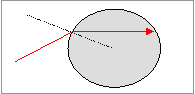
4. Μια φωτεινή ακτίνα προερχόμενη από τον αέρα προσπίπτει σε μία διαφανή σφαίρα, διαθλώμενη εισέρχεται στο εσωτερικό της και προσπίπτει σε σημείο της εσωτερικής επιφάνειας. Να αποδείξετε ότι είναι αδύνατον να συμβεί ολική ανάκλαση

5. Μία μονοχρωματική ακτίνα φωτός διαδίδεται σε κάποιο διαφανές μέσο με ταχύτητα 270.000 km/s και προσπίπτει στην επιφάνεια που διαχωρίζει το μέσο Α ένα άλλο διαφανές μέσο Β υπό γωνία προσπτώσεως 60⁰ . Η ταχύτητα διάδοσης στο μέσο Β είναι 250000 km/s .

α. Η φωτεινή ακτίνα θα υποστεί ολική ανάκλαση

β. Η φωτεινή ακτίνα δεν θα υποστεί ολική ανάκλαση και η γωνία διάθλασης θα είναι μεγαλύτερη από 60⁰ .

γ. Η φωτεινή ακτίνα δεν θα υποστεί ολική ανάκλαση και η γωνία διάθλασης θα είναι μικρότερη από 60⁰ .

Να καταγράψετε αυτό με το οποίο συμφωνείτε και να δικαιολογήσετε την απάντηση

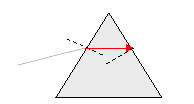
6. Στη μία έδρα πρίσματος προσπίπτει λεπτή δέσμη λευκού φωτός.

Να αποδείξετε ότι το άθροισμα των γωνιών θ₂ + θ₃ είναι ίδιο για όλες τις ακτινοβολίες στις οποίες αναλύεται το λευκό φως. Η θ₂ είναι η γωνία διάθλασης κατά την πρώτη διάθλαση και η θ₃ είναι η γωνία πρόσπτωσης κατά την επόμενη διάθλαση. ( Και οι δύο γωνίες δημιουργούνται στο εσωτερικό του πρίσματος. )

7. Στη μία έδρα πρίσματος προσπίπτει λεπτή δέσμη λευκού φωτός υπό γωνία 30⁰. Εάν είναι γνωστοί οι δείκτες διάθλασης του γυαλιού για την ερυθρή και για την ιώδη ακτινοβολία είναι αντίστοιχα 1,51 και 1,53 να προβλέψετε τη γωνία μεταξύ της ερυθρής και της ιώδους δέσμης μέσα στο γυαλί. Να θεωρήσετε γνωστό ότι ημ19,34⁰ = 50/151 ημ19,07⁰=50/153

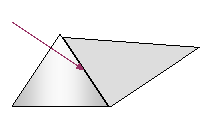
8. Ένα πρίσμα με διατομή ισοπλεύρου τριγώνου και δείκτη διάθλασης √3, είναι προσκολλημένο σε ένα άλλο πρίμα δείκτη διάθλασης √3/√2,όπως στο σχήμα. Μια μονοχρωματική φωτεινή ακτίνα προσπίπτει κάθετα στην ελεύθερη επιφάνεια του πρώτου πρίσματος. Να σχεδιάσετε την πορεία της και να υπολογίσετε την εκτροπή της.

9. Πόση πρέπει να είναι η διαθλαστική γωνία ενός πρίσματος ώστε καμία από τις ακτίνες μιας μονοχρωματικής ακτινοβολίας που προσπίπτει σε μία έδρα του να μην εξέρχεται από την άλλη έδρα. Δίδεται ότι ο δείκτης διάθλασης του πρίσματος για τη συγκεκριμένη μονοχρωματική ακτινοβολία είναι √2.

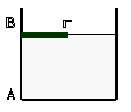
10. Σ’ ένα ορθογώνιο δοχείο με αδιαφανή τοιχώματα βάζουμε νερό μέχρι ύψους ΑΒ = 26, 45 cm. Στη συνέχεια σκεπάζουμε ένα μέρος της επιφάνειας του νερού με αδιαφανή πλάκα ΒΓ, έτσι ώστε η ακμή Α να μην είναι ορατή από οποιοδήποτε σημείο. Να υπολογίσετε το ελάχιστο μήκος ΒΓ της πλάκας ώστε να μη φαίνεται (απ’ έξω) η ακμή Α. Ο δείκτης διάθλασης του νερού είναι ίσος με 4/3.

11. Τρεις φωτεινές μονοχρωματικές ακτίνες του ίδιου χρώματος εκπορεύονται από φωτεινό σημείο του πυθμένα ενός δοχείου με νερό. Η πρώτη προσπίπτει κάθετα στην επιφάνεια του νερού, η δεύτερη προσπίπτει υπό γωνία φ για την οποία ημφ = √8/3 και η τρίτη υπό γωνία 60⁰. Να σχεδιάσετε την πορεία καθεμιάς με δεδομένο ότι ο δείκτης διάθλασης του νερού είναι 4/3.

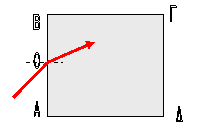
12. Η τομή ενός γυάλινου διαφανούς κύβου είναι τετράγωνο πλευράς 20 cm. Μία μονοχρωματική ακτίνα προερχόμενη από τον αέρα και διαδιδόμενη στο επίπεδο της τομής ΑΒΓΔ ( όπως στο σχήμα ) προσπίπτει στην επιφάνεια του κύβου υπό γωνία 45⁰ στο μέσον Ο της ΑΒ. Να προβλέψετε σε ποιο σημείο του κύβου θα εξέλθει και πάλι στον αέρα. Ο δείκτης διάθλασης του διαφανούς υλικού του κύβου για τη συγκεκριμένη ακτινοβολία είναι √2.

13. Ένα κυλινδρικό δοχείο με αδιαφανή τοιχώματα περιέχει νερό σε βάθος 20 cm. Στο κέντρο του πυθμένα υπάρχει πηγή μονοχρωματικού φωτός. Στην επιφάνεια του νερού επιπλέει αδιαφανής δίσκος διαμέτρου 60 cm έτσι ώστε το κέντρο του να βρίσκεται στην ίδια κατακόρυφο που βρίσκεται και το κέντρο του πυθμένα. Να εξετάσετε εάν η φωτεινή πηγή θα είναι ορατή από κάποιον παρατηρητή που βρίσκεται έξω από το δοχείο.

14. Εκείνη παρατηρεί το χρυσόψαρο μέσα στη γυάλα. Το παρατηρεί από πάνω, το μάτι της δηλαδή βρίσκεται στην ίδια κατακόρυφο με το χρυσόψαρο. Το βλέπει ψηλότερα ή χαμηλότερα από την πραγματική του θέση; Αλλά και το χρυσόψαρο την παρατηρεί. Την βλέπει ψηλότερα ή χαμηλότερα από την πραγματική της ; Να δικαιολογήσετε τις απαντήσεις.

15. Μια μονοχρωματική ακτίνα φωτός προσπίπτει, όπως στο σχήμα, σε διαφανή πλάκα με παράλληλες έδρες άπειρου μήκους και δείκτη διάθλασης √2. Να αποδείξετε ότι΅: α. Εφόσον η πλάκα έχει άπειρο μήκος, το φως θα διατηρείται μέσα σε αυτήν

συνεχώς ανακλώμενο, με οποιονδήποτε τρόπο και να γίνει η πρόσπτωση, και για οποιαδήποτε τιμή του πάχους d της πλάκας.

β. Αν το μήκος της πλάκας είναι L, η εκτροπή θα είναι είτε μηδέν είτε 2θ, (όπου θ η γωνία πρόσπτωσης) και αυτό θα καθορίζεται

από τον λόγο d/L. γ. Αν το μήκος της πλάκας είναι L και η πρόσπτωση γίνει στο μέσον της ΑΒ με γωνία 45⁰ η εκτροπή θα είναι

i . ίση με μηδέν εάν L/d < √3/2 ii . ίση με 90⁰ εάν √3/2 < L/d < 3√3/2 iii. ίση με μηδέν εάν 3√3/2 < L/d < 5√3/2 .

16. Δύο διαφανείς πλάκες απείρου μήκους, η 1 και η 2, με αντίστοιχους δείκτες διάθλασης n₁ = √2 και n₂ = √1,5 βρίσκονται σε επαφή, όπως στο σχήμα. Μια μονοχρωματική ακτίνα φωτός προερχόμενη από τον αέρα προσπίπτει, σε σημείο της διαχωριστικής επιφάνειας της 1 (σχήμα) υπό γωνία θ α. Να αποδείξετε ότι οποιαδήποτε και να είναι η τιμή της θ δεν θα συμβεί ολική ανάκλαση β. Να προβλέψετε την εκτροπή της, τη γωνία δηλαδή μεταξύ της αρχικά προσπίπτουσα στην πλάκα 1 και την εξερχόμενη από την πλάκα 2 γ. Να υπολογίσετε τις τιμές όλων των γωνιών διάθλασης σε περίπτωση που θ = 45⁰. Να θεωρήσετε ότι ημ39⁰ = 0,57