Ανδρέας Ιωάννου Κασσέτας

Για την επιτάχυνση της βαρύτητας να θεωρήσετε ότι η τιμή της είναι 10m/s² .

Όλα τα αντικείμενα είναι ομογενή και συμπαγή, εκτός εάν αναφέρεται κάτι διαφορετικό

Για τη ροπή αδράνειας ορισμένων συμπαγών και ομογενών σωμάτων ως προς συγκεκριμένο άξονα συμμετρίας να θεωρήσετε γνωστό ότι

1. Η στροφική κίνηση ενός δίσκου ακτίνας 20 cm περί άξονα κάθετο στο επίπεδό του περιγράφεται με το διάγραμμα γωνιακής ταχύτητας και χρόνου σε μονάδες SI.

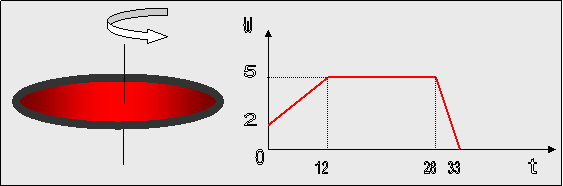
Σας ζητούμε να κάνετε τη γραφική παράσταση γωνιακής επιτάχυνσης και χρόνου για το αντίστοιχο χρονικό διάστημα και να προσδιορίσετε

α. την ταχύτητα ενός σημείου της περιφέρειας κατά τις χρονικές στιγμές 10 s, 21 s και 30 s

β. την ταχύτητα ενός σημείου που απέχει 8 cm από τον άξονα περιστροφής κατά τη χρονική στιγμή 10 s

γ. την εφαπτομενική (επιτρόχια ) επιτάχυνση ενός σημείου της περιφέρειας κατά τις χρονικές στιγμές 7 s και 21 s

δ. την επιτάχυνση ενός σημείου της περιφέρειας τη χρονική στιγμή 19 s .

( Απ. α. 0,9m/s, 1 m/s 0,6 m/s β. 0,36 m/s, γ. 0,05m/s² και μηδέν δ. 5m/s²)

2. Μια μπίλια ακτίνας 10 cm αφήνεται από την κορυφή κεκλιμένου επιπέδου γωνίας φ και κυλίεται χωρίς ολίσθηση.

Η γωνία φ του κεκλιμένου επιπέδου με το οριζόντιο επίπεδο είναι τέτοια ώστε το κέντρο μάζας της να έχει επιτάχυνση

1 m/s² . Ας είναι Α το υλικό σημείο της μπίλιας το οποίο βρίσκεται σε επαφή με το κεκλιμένο επίπεδο τη στιγμή που αφήνεται. Πόσες φορές ακόμα το υλικό σημείο Α θα ακουμπήσει στο κεκλιμένο επίπεδο κατά τη διάρκεια των

2 πρώτων δευτερολέπτων της κίνησης ; Ποια θα είναι η ταχύτητα του κέντρου μάζας τη χρονική στιγμή t_α που το υλικό σημείο Α αγγίζει την επιφάνεια του κεκλιμένου επιπέδου για τέταρτη φορά ; Ποια θα είναι η επιτάχυνση του Α κατά τη στιγμή t_α ; (Απ. 3 φορές , 2,24 m/s, 16π m/s²)

3. H ομογενής ράβδος, ισορροπεί στον κατακόρυφο

τοίχο και στο έδαφος.

Η τριβή στον τοίχο είναι αμελητέα

και στην επαφή ράβδου εδάφους

ο συντελεστής στατικής τριβής είναι 0,5.

Να προσδιορίσετε a. τη μικρότερη γωνία

με το οριζόντιο έδαφος για την οποία η ράβδος ισορροπεί

β. την τροχιά του κέντρου μάζας κατά την ολίσθηση της ράβδου μέχρι να οριζοντιωθεί στο έδαφος

( Απ. 45⁰ )

4. Να προσδιορίσετε τις δυνάμεις που ασκούνται τριγωνική πλάκα

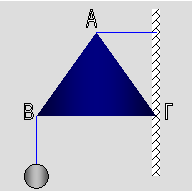η οποία έχει βάρος 30 Ν

και σχήμα ισόπλευρου τριγώνου.

Στο σημείο Γ στηρίζεται με άρθρωση

στον κατακόρυφο τοίχο,

ενώ στο σημείο Α

υπάρχει οριζόντιο τεντωμένο

νήμα με το οποίο στηρίζεται

στον ίδιο τοίχο

Στην κορυφή Β κρέμεται,

με σπάγκο, ένα βαρίδι

– σημειακό αντικείμενο - μάζας 1 kg.

( Απ. mg = 30N F_νΒ= 10 Ν F_νΑ = 28,9 Ν F_Γ = 49,3 Ν )

5. Μια σκάλα μήκους 5 m και βάρους 200 Ν υποβαστάζεται κατά το ένα άκρο

της με ένα οριζόντιο συρματόσκοινο

μήκους 3 m από τον κατακόρυφο τοίχο.

Το κάτω άκρο της στηρίζεται στη

γωνία τοίχου και εδάφους.

Ένα κορίτσι 50 kg ανεβαίνει στη σκάλα.

Πόσο ψηλά μπορεί να ανέβει

χωρίς να σπάσει το οριζόντιο

συρματόσκοινο ;

Το συρματόσκοινο έχει

όριο θραύσεως 360 Ν.

Αυτό σημαίνει ότι αν η δύναμη

που ασκεί ξεπεράσει τα 360Ν

το συρματόσκοινο θα σπάσει .

( Απ. 3,04 m )

6. Μία ομογενής ράβδος AB μάζας 3kg κρέμεται από δύο ίσα νήματα ΑΟ και ΒΟ

από ένα σημείο Ο στο ταβάνι.

Κρεμάμε ένα βαρίδι 10 Ν από ένα σημείο Δ

της ράβδου, για το οποίο ισχύει (ΑΒ) = 4(ΑΔ).

Η ράβδος ισορροπεί σε μια νέα θέση.

Να υπολογίσετε τον λόγο των δύο δυνάμεων

τις οποίες ασκούν τα νήματα ΑΟ και ΒΟ

στα άκρα Α και Β της ράβδου.

( Απ. λ = 7/9 )

7. Μία ομογενής ράβδος ΑΒΓ κάμπτεται

στο σημείο Β οπότε δημιουργείται

ένα μεταλλικό στέλεχος με δύο σκέλη ΑΒ και ΒΓ,

έτσι ώστε ΒΓ = 2ΑΒ και η γωνία ΑΒΓ να είναι 60⁰.

Κρεμάμε το στέλεχος

από το σημείο Α

με κατακόρυφο νήμα ΑΜ.

Να προσδιορίσετε τη γωνία

την οποία σχηματίζει το σκέλος ΒΓ

με το οριζόντιο επίπεδο.

( Απ. εφφ = √3/5)

8. Ένα κουτί βρίσκεται ακίνητο σε οριζόντιο τραπέζι. Αν το σπρώξουμε με οριζόντια δύναμη ορισμένης τιμής μέχρι και 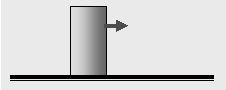σε ύψος 12 cm θα το κάνουμε να μετατοπιστεί οριζόντια. Αν το ύψος στο οποίο ασκούμε την οριζόντια δύναμη ξεπεράσει τα 12 cm το κουτί ανατρέπεται. Να προσδιορίσετε τον συντελεστή στατικής τριβής ανάμεσα στη επιφάνεια του κουτιού και το τραπέζι . Δίνεται ότι η βάση του κουτιού έχει μήκος

– σε διεύθυνση παράλληλη προς εκείνης της ασκούμενης

οριζόντιας δύναμης - 6 cm. (Απ. μ = 0,25)

9. Ένας ομογενής κύλινδρος ακτίνας 40 cm στρέφεται με γωνιακή ταχύτητα 60 rad/s

και πρόκειται να τοποθετηθεί έτσι ώστε να βρίσκεται σε επαφή

και με το κατακόρυφο τοίχωμα

και με την οριζόντια επιφάνεια, όπως στο σχήμα.

Να προβλέψετε πότε θα σταματήσει

εάν είναι γνωστή η τιμή μ = 0, 3

του συντελεστή τριβής,

ίδια και για τις δύο επαφές του. (Απ. 3,35 s )

10. Αρχικά το νήμα είναι τεντωμένο και συγκρατεί την οριζόντια ομογενή ράβδο ΟΑ

η οποία αρθρώνεται στο άκρο της Ο.

Σε κάποια στιγμή κόβουμε το νήμα.

Κατά τη χρονική στιγμή που έχει κοπεί το νήμα

να υπολογίσετε

α. την επιτάχυνση του άκρου Α της ράβδου και

β. τον λόγο F_a/mg όπου F_a η δύναμη που ασκεί

η άρθρωση στη ράβδο και mg το βάρος της ράβδου.

(Απ. α. 3g/2, β. ¼ )

11. Μια μπίλια 300 g αφήνεται να κυλήσει από την κορυφή κεκλιμένου επιπέδου γωνίας 30⁰ . Να προσδιορίσετε

α. την επιτάχυνση του κέντρου μάζας β. τις τιμές όλων των δυνάμεων που ασκούνται στη μπίλια κατά την κύλισή της.

(Απ. α. 5g/14 β , mg = 3 N . Τ_σ = 3/7 Ν N= 1,5.√3 N )

12. Πόση πρέπει να είναι η γωνία ενός κεκλιμένου επιπέδου ώστε αν αφήσουμε μια μπίλια να κυλήσει χωρίς ολίσθηση;

Δίνεται ο συντελεστής στατικής τριβής ίσος με ²/₇ . (Απ. φ < 45⁰)

13. Σε μία χρονική στιγμή που θεωρείται αρχή των χρόνων, σε μία ομογενή σφαίρα, αρχικά ακίνητη, ασκείται ολική ροπή η οποία διατηρείται σταθερή ίση με 0, 25 Νm και η σφαίρα στρέφεται περί έναν άξονα συμμετρίας.

Αν η ροπή αδράνειας ως προς τον άξονα περιστροφής είναι 10^-2 kgm² ,

Σας ζητούμε κατά τη χρονική στιγμή 4s να υπολογίσετε α. την κινητική ενέργεια της σφαίρας και

β. την ταχύτητα ενός σημείου της επιφάνειας που απέχει 30 cm από τον άξονα περιστροφής .

(Απ. α. 50 J β. 30 m/s)

14. Το κέντρο μάζας ενός ομογενούς δίσκου διατηρείται ακινητοποιημένο. Σε κάποια χρονική στιγμή – αρχή των χρόνων - κατά την οποία ο δίσκος είναι ακίνητος ασκείται σταθερή δύναμη 10 Ν στην περιφέρειά του από ένα νήμα τυλιγμένο γύρω του . Ο δίσκος εκτελεί στροφική κίνηση περί άξονα κάθετο στο επίπεδό του. 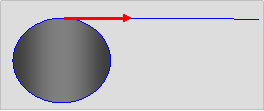Διαπιστώνεται ότι σε μια χρονική στιγμή t_a της κίνησης η κινητική ενέργεια του δίσκου είναι 4 J και η κεντρομόλος επιτάχυνση ενός σημείου της περιφέρειας 8 m/s² .

α. Βασιζόμενοι στα δεδομένα αυτά να υπολογίσετε τη γωνιακή επιτάχυνση του δίσκου .

β. Αν σας δοθεί επιπλέον ότι η ακτίνα του δίσκου είναι 60 cm , να υπολογίσετε τη μάζα του και την επιτάχυνση ενός σημείου της περιφέρειας τη χρονική στιγμή t_a .

( Απ. α. 10 rad/s² β.10/3 kg, 10 m/s²)

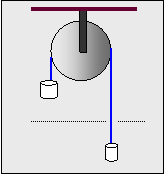15. Μετρώντας τη μάζα

με μετροταινία και χρονόμετρο

Τα δύο αντικείμενα αφήνονται

ελεύθερα σε κάποια στιγμή

που βρίσκονται στο ίδιο ύψος.

Με μετροταινία και χρονόμετρο

διαπιστώνεται ότι μετά

από 3 δευτερόλεπτα

θα απέχουν υψομετρικά 90 cm.

Αν οι μάζες τους είναι 210g,

και 200g να υπολογίσετε τη μάζα της τροχαλίας ( Απ. 1,18 kg)

16. Ένας αρχικά ακίνητος ομογενής δίσκος ακτίνας 40 cm και μάζας 6 kg μπορεί να στρέφεται

περί άξονα κάθετο 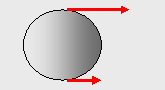στο επίπεδό του διερχόμενο από το κέντρο του. Κατά τη χρονική στιγμή

τη θεωρούμενη ως αρχή των χρόνων στον δίσκο ασκούνται

δύο δυνάμεις F₁ = 60Ν και F₂ = 45Ν όπως στο σχήμα οι οποίες εξακολουθούν να ασκούνται με τον ίδιο τρόπο επί 10 s

Σας ζητούμε να υπολογίσετε a. την κινητική ενέργεια του δίσκου τη χρονική στιγμή 4 s

β. την τιμή της ταχύτητας ενός σημείου το οποίο απέχει 10 cm από το κέντρο, τη στιγμή 6 s γ. την τιμή της εφαπτομενικής ( επιτρόχιας ) επιτάχυνσης ενός σημείου της περιφέρειας τις χρονικές στιγμές 2 s και 10 s

( Απ. α. 600 J β. 7,5 m/s γ. 5 rad/s²)

17. Μία ράβδος ακινητεί σε οριζόντιο έδαφος χωρίς τριβή. Κάποιος τη σπρώχνει με οριζόντια δύναμη κάθετα στη διεύθυνσή της σε απόσταση d από το κέντρο μάζας. Σε ποιο σημείο πρέπει να την κρατάμε για να νιώσουμε το ασθενέστερο τράνταγμα ; Τα δεδομένα είναι το μήκος L της ράβδου και η απόσταση d .

Υπενθυμίζεται ότι η ροπή

αδράνειας της ράβδου I_cm

ως προς άξονα κάθετο

σ’ αυτή που περνά

από το κέντρο μάζας

δίνεται από τη σχέση

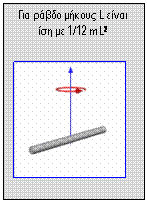
I_cm = 1/12 mL² όπου

m η μάζα της.

Σχόλιο .Το σημείο στο οποίο πρέπει να την κρατάμε για να νιώσουμε το ασθενέστερο τράνταγμα είναι το σημείο εκείνο που αποκτά μηδενική επιτάχυνση. Εφόσον η δύναμη δεν ασκείται στο κέντρο μάζας - και η ράβδος είναι αρχικά ακίνητη - η κίνηση της θα είναι σύνθετη μεταφορική με την επιτάχυνση του κέντρου μάζας και στροφική περί κατακόρυφο άξονα που περνά από το κέντρο μάζας

( Απ. x = L²/12d )

18. Ένας μεγάλος δίσκος έχει μάζα 800 g και ακτίνα 10 cm.

Ένας μικρότερος έχει ακτίνα 6 cm και αμελητέα μάζα.

Οι δύο δίσκοι προσαρμόζονται στον ίδιο

άξονα ώστε να κινούνται ως ένα στρεφόμενο σώμα.

Δύο αντικείμενα Σ₁ και Σ₂ με μάζες 600 g και 400 g

δένονται από νήματα αμελητέας μάζας (σχήμα) και

το σύστημα αφήνεται ελεύθερο σε χρονική στιγμή

την οποία θεωρούμε αρχή των χρόνων

Να υπολογίσετε

α. την επιτάχυνση κάθε αντικειμένου.

β. τη στροφορμή του στρεφομένου σώματος τη χρονική στιγμή 3 s

Το νήμα του Σ₁ βρίσκεται μακρύτερα από το άλλο νήμα από τον άξονα

περιστροφής και τα αντικείμενα υλικά σημεία.

( Απ. α. 3, 14 m/s² 1,89 m/s² β. 0,38 Js)

19. Δύο λεπτές ισοπαχείς και ομογενείς ράβδοι ΟΑ και ΟΒ, που έχουν μάζα Μ = 4kg και μήκος L=1,5m η καθεμία, συγκολλώνται στο ένα άκρο τους Ο ώστε να σχηματίζουν ορθή γωνία και συγκροτούν ένα σώμα .

Το σώμα αυτό μπορεί να περιστρέφεται περί οριζόντιο άξονα, κάθετο στο επίπεδο ΑΟΒ, που διέρχεται από την κορυφή Ο της ορθής γωνίας.

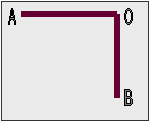Το σύστημα αρχικά συγκρατείται στη θέση όπου η ράβδος ΟΑ είναι οριζόντια (όπως στο σχήμα). Η ροπή αδράνειας της κάθε ράβδου ως προς το κέντρο μάζας της είναι I_cm = 1/12 ML² .

a. Να υπολογίσετε τη ροπή αδράνειας της κάθε ράβδου ως προς τον άξονα περιστροφής που διέρχεται από το Ο.

β. Από την αρχική του θέση το σύστημα των δύο ράβδων αφήνεται ελεύθερο να περιστραφεί περί τον άξονα περιστροφής στο σημείο Ο, χωρίς τριβές. Να υπολογίσετε το μέτρο της γωνιακής επιτάχυνσης του συστήματος των δύο ράβδων τη στιγμή της εκκίνησης.

γ. Τη χρονική στιγμή κατά την οποία οι ράβδοι σχηματίζουν ίσες γωνίες με την κατακόρυφο Ox, να προσδιορίσετε :

i. Τη γωνιακή ταχύτητας του σώματος - συστήματος των δύο ράβδων και

ii . Την ως προς Ο στροφορμή του συστήματος των δύο ράβδων Δίνονται ημ45⁰ = συν45⁰= 0,7.

( Απ. α. 3 kgm² β. 5 rad/s² γ. 2 rad/s 12 Js )

20. Ένας ομογενής λεπτός χάρακας μήκους L = 60 εκατοστών έχει επτά ισαπέχουσες τρύπες, όλες στην ίδια ευθεία αβ, έτσι ώστε η πρώτη τρύπα να βρίσκεται στο άκρο του χάρακα, η τέταρτη στο κέντρο βάρους του και η έβδομη στο άλλο άκρο.

Περνάμε μέσα από τη δεύτερη τρύπα ένα σκληρό σύρμα διατηρούμενο κάθετο στον άξονα του και οριζόντιο. Κρατάμε τον χάρακα σε οριζόντια θέση και τον αφήνουμε ελεύθερο.

Να υπολογίσετε α. τη γωνιακή επιτάχυνση του χάρακα τη στιγμή που τον αφήνουμε

β. τη γωνιακή ταχύτητα του χάρακα τη στιγμή που θα γίνει κατακόρυφος.

γ. τη γωνιακή επιτάχυνση του χάρακα τη στιγμή που θα γίνει κατακόρυφος.

Η ροπή αδράνειας του χάρακα ως προς άξονα κάθετον σ’ αυτόν και διερχόμενο από το κέντρο μάζας δίνεται από την Ι = ¹/₁₂ mL², όπου m η μάζα του

( Απ. α. 25 rad/s² β.5√2 rad/s γ. μηδέν ) )

21. Δύο όμοιες σφαίρες αφήνονται ταυτόχρονα και από το ίδιο ύψος, η μία δίπλα στην άλλη, στη κορυφή κεκλιμένου επιπέδου και κατέρχονται μέχρι τη βάση. Η μια (Σ₁ ) κατέρχεται κυλιόμενη χωρίς ολίσθηση. Η άλλη (Σ₂ ) είναι καλυμμένη με λιπαντικό –το οποίο έχει εκμηδενίσει την τριβή- και ολισθαίνει χωρίς να κυλίεται.

α. Η μεταβολή στην κινητική ενέργεια της Σ₁ (κατά την κίνηση της από την κορυφή έως τη βάση) είναι ίση με τη μεταβολή στην κινητική ενέργεια της Σ₂, κατά τη «δική της» κίνηση από την κορυφή έως τη βάση

β. Κατά την κίνηση της Σ₁ το άθροισμα κινητικής και δυναμικής ενέργειας διατηρείται σταθερό

γ. Οι δύο σφαίρες φθάνουν στη βάση ταυτόχρονα.

δ. Σε δεδομένη χρονική στιγμή -και ενώ κινούνται κατερχόμενες- οι δύο σφαίρες έχουν την ίδια δυναμική ενέργεια ως προς το έδαφος

Με ποια από τα παραπάνω συμφωνείτε ; Να δικαιολογήσετε την απάντηση

22. Μια σφαίρα και ένας κύλινδρος αφήνονται από την κορυφή κεκλιμένου επιπέδου κυλούν προς τα κάτω χωρίς ολίσθηση και φθάνουν στη βάση του κεκλιμένου . Με ποια από τις προτάσεις συμφωνείτε;

a) Ο κύλινδρος θα διανύσει την απόσταση σε λιγότερο χρόνο και αυτό είναι ανεξάρτητο της μάζας και της ακτίνας των αντικειμένων.

β) Το σώμα με τη μεγαλύτερη μάζα θα διανύσει την απόσταση σε λιγότερο χρόνο

γ) Θα διανύσουν την απόσταση και τα δύο συγχρόνως, ανεξάρτητα από τη μάζα και την ακτίνα των δύο αντικειμένων

δ) Η σφαίρα θα διανύσει την απόσταση σε λιγότερο χρόνο και αυτό είναι ανεξάρτητο της μάζας και της ακτίνας των δύο αντικειμένων.

23. Ένα ποδήλατο κινείται έτσι ώστε η ταχύτητα του κέντρου βάρους του να είναι σταθερή και ίση με 36km/h. Κάθε τροχός του έχει ακτίνα 40 cm και μάζα 5 kg θεωρούμενη συγκεντρωμένη στην περιφέρειά του.

a. Να προσδιορίσετε τη στροφορμή κάθε τροχού κατά τον άξονα περιστροφής. Ο ποδηλάτης φρενάρει, η ταχύτητά του μειώνεται γραμμικά και το ποδήλατο σταματάει μετά από 4 s. Να προσδιορίσετε β. τον ρυθμό μεταβολής της στροφορμής κάθε τροχού και γ. τη δύναμη τριβής που ασκήθηκε από τα φρένα.

( Απ. α. 20 Js β. 5 Nm γ. 12,5 Ν )

24. Ένας ποδηλάτης κρατάει το ποδήλατο του από το τιμόνι έτσι ώστε ο μπροστινός τροχός μάζας 2kg και ακτίνας 30 cm στρεφόμενος να μην ακουμπάει στο έδαφος. Ενώ ο μπροστινός αυτός τροχός στρέφεται με γωνιακή ταχύτητα 6 rad/s, ο ποδηλάτης στρέφει τον άξονά του τροχού κατά 60⁰ προς τα αριστερά.

α. Να προσδιορίσετε τη μεταβολή της στροφορμής του τροχού.

β. Αν είναι γνωστό ότι η στροφή έγινε σε χρόνο 0,2s να προσδιορίσετε τη ροπή που άσκησε ο ποδηλάτης στο τιμόνι.

Η μάζα του τροχού θεωρείται συγκεντρωμένη στην περιφέρειά του.

( Απ. α. 1,08 Js β. 5,4. Nm )

25. Το γιο-γιο του σχήματος αποτελείται από έναν κύλινδρο γύρω από τον οποίο έχει τυλιχτεί κάποιο νήμα. Διατηρούμε τον κύλινδρο ακίνητο με το νήμα τεντωμένο και κατακόρυφο ενώ το άνω άκρο του νήματος προσδένεται σε σταθερό σημείο.

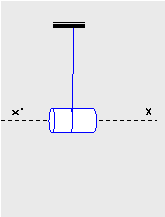Σε κάποια χρονική στιγμή την οποία θεωρούμε t = 0 αφήνουμε ελεύθερο τον κύλινδρο και αυτός κινείται έτσι ώστε το κέντρο μάζας του να κατευθύνεται κατακόρυφα προς τα κάτω ενώ το νήμα να διατηρείται τεντωμένο και κατακόρυφο χωρίς να ολισθαίνει στην περιφέρεια του κυλίνδρου. Ο κύλινδρος θεωρείται συμπαγής έχει μάζα 0,12 kg και ακτίνα R = 1,5 10^-2 m.

Τη στιγμή που έχει ξετυλιχτεί νήμα μήκους 20R η ταχύτητα του κέντρου μάζας του κυλίνδρου είναι 2 m/s. Βασιζόμενοι στα παραπάνω και σε νόμους της φυσικής να υπολογίσετε

α. τη ροπή αδράνειας του κυλίνδρου ως προς τον οριζόντιο άξονα συμμετρίας x ΄x ( σχήμα ) ο οποίος διέρχεται από το κέντρο μάζας του. Δεν θα θεωρήσετε γνωστό ότι η ροπή αδράνειας δίνεται από την εξίσωση Ι = ½mR².

β. Θεωρώντας ότι η κίνηση του κυλίνδρου αναλύεται σε μεταφορική και στροφική περί άξονα

x ΄x να υπολογίσετε τη τον ρυθμό μεταβολής της στροφορμής για τη στροφική κίνηση κατά τον άξονα x΄x , σε μια οποιαδήποτε στιγμή της κίνησης.

γ. Τη χρονική στιγμή που το κέντρο μάζας του κυλίνδρου έχει ταχύτητα 2m/s το νήμα κόβεται. Η κίνηση που ακολουθεί μπορεί να αναλυθεί σε μεταφορική με επιτάχυνση g και σε στροφική περί τον άξονα x΄x

Να υπολογίσετε τη στροφορμή του κυλίνδρου κατά τον άξονα x΄x σε μια οποιαδήποτε χρονική στιγμή αυτής της κίνησης

δ. Σε άξονες τους οποίους έχετε βαθμολογήσει να σχεδιάσετε το διάγραμμα των αλγεβρικών τιμών της στροφορμής κατά τον άξονα x΄x σε συνάρτηση με τον χρόνο από τη χρονική στιγμή t = 0 μέχρι τη στιγμή που αντιστοιχεί σε 0,8 s μετά το κόψιμο του νήματος

( Απ. α. 13,5.10^-6 kgm² . β. 6. 10^-3 Nm γ. 18.10^-4 Js )

26. Το μολύβι μήκους L ισορροπεί κατακόρυφο στο άκρο του δακτύλου μας. Το αφήνουμε και εκείνο ( με ασήμαντη αρχική ταχύτητα του κέντρου μάζας ) ανατρέπεται, φθάνει σε οριζόντια θέση κατά τη χρονική στιγμή t₁ και στη συνέχεια κινείται προς το πάτωμα.

a. Να υπολογίσετε τη γωνιακή ταχύτητα του μολυβιού τη στιγμή που γίνεται οριζόντιο

β. Να περιγράψετε την κίνηση του μολυβιού αφού εγκαταλείψει το χέρι μας καθώς το κέντρο μάζας κινείται προς το πάτωμα

γ. Να υπολογίσετε το χρονικό διάστημα από τη χρονική στιγμή t₁ που «εγκαταλείπει» το χέρι μας μέχρι τη στιγμή που το κέντρο μάζας του μολυβιού θα έχει κατέλθει κατά h. Το μολύβι να θεωρηθεί ομογενής ράβδος . Δίνονται τα L= 20 cm και h = 1m .

( Απ. α. √3g/√L = 12,25 rad/s γ. 0,34 S )

27. Η μπίλια αφήνεται από

το σημείο Α του κεκλιμένου

επιπέδου, κυλίεται μέχρι

τη βάση του, στη συνέχεια

κυλίεται στον σφαιρικό

αγωγό, σχήματος

τεταρτοκυκλίου, διαγράφει

τόξο 90⁰ μοιρών και στη

συνέχεια κινείται έτσι

ώστε το κέντρο μάζας της

να εκτελεί κατακόρυφη κίνηση προς τα πάνω.

Με δεδομένα το ύψος h του σημείου Α, την ακτίνα R του τεταρτοκυκλίου και την τιμή της βαρυτικής επιτάχυνσης

α. Να προσδιορίσετε την ταχύτητα του κέντρου μάζας τη στιγμή που φθάνει στο υψηλότερο σημείο Γ του τεταρτοκυκλίου

β. Να προσδιορίσετε την κίνηση που θα ακολουθήσει κατά την ανοδική κατακόρυφη κίνηση

γ. Να υπολογίσετε το μέγιστο ύψος στο οποίο θα φθάσει.

( Απ. α. √10g(h–R)/7 γ. 5h/7 + 2R/7 )

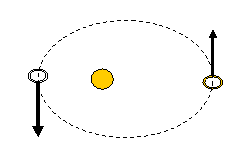28. Κατά την ετήσια περιφορά της

γύρω από τον Ήλιο, όταν

η Γη βρίσκεται στο περιήλιο

η ταχύτητά της είναι υ₁ και

η απόσταση από τον Ήλιο R₁,

ενώ όταν βρίσκεται στο αφήλιο

οι αντίστοιχες τιμές είναι υ₂ και R₂.

Να υπολογίσετε τον λόγο

των ταχυτήτων υ₁ / υ₂ με δεδομένο τις δύο αποστάσεις. ( Απ. R₂/R₁ )

29. Ένα κομμάτι λάσπης, μάζας m, κινούμενο οριζόντια με ταχύτητα υ πέφτει «εφαπτομενικά» σε δίσκο μάζας Μ, στρεφόμενο με γωνιακή ταχύτητα ω₁ και ενσωματώνεται σε σημείο Α . Η ταχύτητα του κομματιού πριν την ενσωμάτωση έχει την ίδια κατεύθυνση με την ταχύτητα του σημείου Α του δίσκου . Βασιζόμενοι σε φυσικούς νόμους να προβλέψετε τη γωνιακή ταχύτητα ω₂ του συσσωματώματος

Το κομμάτι της λάσπης να θεωρηθεί υλικό σημείο. ( Απ. ω₂ = (2mυR+ MR²ω₁)/(2mR²+MR² )

30. Ένα κομμάτι λάσπης - υλικό σημείο μάζας m - αφήνεται από ύψος h, πέφτει κατακόρυφα στην άκρη ενός δίσκου μάζας Μ στρεφόμενου με γωνιακή ταχύτητα ω₁ και ενσωματώνεται. Αν Μ = 28m να προβλέψετε τη γωνιακή ταχύτητα ω₂ του συσσωματώματος. Απ. ω₂ = 14ω₁/15

31. Μία κατακόρυφη ράβδος μήκους L και μάζας Μ μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο περί οριζόντιο άξονα ο οποίος διέρχεται από το ανώτερο άκρο της. Ένα βλήμα μάζας m κινούμενο με οριζόντια ταχύτητα υ προσπίπτει κάθετα στη ράβδο και ενσφηνώνεται σε απόσταση d από τον άξονα περιστροφής. Μετά την ενσφήνωση το συσσωμάτωμα στρέφεται κατά γωνία μικρότερη της ορθής μέχρι να μηδενιστεί για πρώτη φορά η ταχύτητά του. Να υπολογίσετε

α. την κινητική ενέργεια (του συσσωματώματος) αμέσως μετά την ενσφήνωση

β. την ταχύτητα του κατώτερου σημείου της ράβδου κατά τη στιγμή εκείνη.

γ. τη μέγιστη γωνία κατά την οποία θα στραφεί η ράβδος με το ενσωματωμένο βλήμα

Δίνονται τα μεγέθη L , Μ, m, d, η βαρυτική επιτάχυνση g και η ροπή αδράνειας της ράβδου ως προς τον άξονα περιστροφής.

32. Μια πόρτα μάζας Μ και πλάτους L είναι ανοιχτή και κάθετη στον τοίχο. Ένα βλήμα μάζας m κινούμενο με οριζόντια ταχύτητα υ προσπίπτει κάθετα στην πόρτα και ενσφηνώνεται στο κέντρο της. Να υπολογίσετε σε πόσο χρόνο θα κλείσει η πόρτα.

Δίνεται η ροπή αδράνειας της πόρτας ως προς τον άξονα της περιστροφής Ι = 1/3 ΜL².

( Απ. t = πL(4M+3m)/12mυ )

33. Μία ράβδος μήκους L = 1 m και μάζας Μ ισορροπεί οριζόντια στηριζόμενη σε κατακόρυφο άξονα που περνά από κέντρο βάρους της. Ένα βλήμα μάζας m κινούμενο με οριζόντια ταχύτητα προσπίπτει κάθετα στη ράβδο σε σημείο που απέχει d = L/4 από το μέσον της, ενσφηνώνεται στην ομογενή ράβδο και το σύστημα αρχίζει να στρέφεται σε οριζόντιο επίπεδο με σταθερή γωνιακή ταχύτητα. Διαπιστώνεται ότι σε χρόνο 41π/400 s εκτελεί μία πλήρη περιστροφή. Με δεδομένο ότι Μ = 30m σας ζητούμε να υπολογίσετε

α. την ταχύτητα του βλήματος πριν από την ενσφήνωση και β. την % ελάττωση της κινητής ενέργειας του συστήματος.

( Απ. α. 200 m/s β. 97,4 % )

34. Ένας οριζόντιος δίσκος μάζας Μ και ακτίνας R στρέφεται, με σταθερή γωνιακή ταχύτητα ω, περί κατακόρυφο άξονα ο οποίος διέρχεται από το κέντρο βάρους του. Σε κάποια στιγμή ένα μικρό τεμάχιο του δίσκου, θεωρούμενο υλικό σημείο μάζας m, αποσπάται από το άκρο του δίσκου και εκτοξεύεται εφαπτομενικά με οριζόντια ταχύτητα ίση με την ταχύτητα που είχε ως τμήμα του δίσκου . Να υπολογίσετε τη γωνιακή ταχύτητα του δίσκου μετά την εκτόξευση

35. Ο τροχός είναι αρχικά ακίνητος σε οριζόντια επιφάνεια με αμελητέα τριβή.

Τι θα συμβεί εάν ασκηθεί και συνεχίσει να ασκείται οριζόντια δύναμη

α. σε ύψος ίσο με την ακτίνα του R β. σε ύψος 2R ίσο με τη διάμετρο. γ. σε ύψος ίσο με 1,5 R

36. Ο τροχός βάρους Β είναι αρχικά ακίνητος σε οριζόντιο έδαφος με συντελεστή ( στατικής ) τριβής μ = 0,4.

Τι θα συμβεί εάν ασκηθεί και συνεχίσει να ασκείται οριζόντια δύναμη F σε ύψος ίσο με την ακτίνα

α. εάν F = 2B β. εάν F = B

.