![]()
 Πιάνει στα χέρια του το τριαντάφυλλο και το
παρατηρεί προσεκτικά . Διαπιστώνει ότι πάνω στο λουλούδι τα ροδοπέταλα
διατάσσονται σε σπειροειδή μορφή. Παίρνει ένα μαχαιράκι και κόβει το λουλούδι.
Ξεκινώντας από το κέντρο καταγράφει μια ομάδα με 5 ροδοπέταλα , που
ξεφυτρώνουν από την ίδια περιοχή, η αμέσως ευρύτερη ομάδα έχει (
συμπεριλαμβανόμενης των πετάλων της προηγούμενης ) 8 ροδοπέταλα συνολικά, η επόμενη μεγαλύτερη ομάδα
Πιάνει στα χέρια του το τριαντάφυλλο και το
παρατηρεί προσεκτικά . Διαπιστώνει ότι πάνω στο λουλούδι τα ροδοπέταλα
διατάσσονται σε σπειροειδή μορφή. Παίρνει ένα μαχαιράκι και κόβει το λουλούδι.
Ξεκινώντας από το κέντρο καταγράφει μια ομάδα με 5 ροδοπέταλα , που
ξεφυτρώνουν από την ίδια περιοχή, η αμέσως ευρύτερη ομάδα έχει (
συμπεριλαμβανόμενης των πετάλων της προηγούμενης ) 8 ροδοπέταλα συνολικά, η επόμενη μεγαλύτερη ομάδα
(
συμπεριλαμβανόμενων και των εσωτερικών) περιλαμβάνει συνολικά 13,
η
επόμενη 21 και το σύνολο είναι 34 ροδοπέταλα.
Οι
συγκεκριμένοι αριθμοί του κάνουν εντύπωση . Τα ροδοπέταλα διατάσσονται έτσι
ώστε οι αριθμοί που προκύπτουν να είναι
όροι
της ακολουθίας Fibonacci.
1, 1, 2, 3,
5, 8, 13, 21, 34, 55. . .
Καθένας από τους όρους της προκύπτει από το άθροισμα των δύο που
προηγούνται.
Σε γλώσσα
Άλγεβρας αν = αν-1
+ αν-2
Στο
τριαντάφυλλο τα ροδοπέταλα που μέτρησε εκείνος ήταν τριαντατέσσερα.
Σε ρόδο με
περισσότερα πέταλα θα είναι πενήντα πέντε.

Αν φτιάξουμε μια νέα ακολουθία με
όρους τους λόγους των διαδοχικών όρων της προηγούμενης θα έχουμε
3/2, 5/3, 8/5, 13/8, 21/13, 34/21. . - με προσέγγιση θα είναι 1,5, 1,667,
1,6, 1,625, 1,615
1,619 . . - και θα διαπιστώσουμε ότι συγκλίνει προς έναν αριθμό. Μπορούμε να αποδείξουμε ότι ο
αριθμός προς τον οποίο συγκλίνει η ακολουθία θα είναι ο φ, ο αριθμός (1+Ö5) /2 ή - με τρία δεκαδικά - ίσος με
1, 618, ο αριθμός που αντιστοιχεί στη ΧΡΥΣΗ
ΤΟΜΗ.
Χωρίζουμε
ένα ευθύγραμμο τμήμα σε δύο κομμάτια. Στη γλώσσα της ελληνικής Γεωμετρίας λέμε
ότι κάνουμε μια ΤΟΜΗ η οποία είναι ΧΡΥΣΗ εφόσον ο λόγος του μεγάλου προς το
μικρό είναι ίσος με το λόγο ολόκληρου προς το μεγάλο.

 O Leonardo Fibonacci,
ένας από τους μεγαλύτερους μαθηματικούς του
Μεσαίωνα, γεννήθηκε τον 12ο αιώνα στην Πίζα της Τοσκάνα γι αυτό και
οι Ιταλοί τον λένε και Leonardo da Pisa.
O Leonardo Fibonacci,
ένας από τους μεγαλύτερους μαθηματικούς του
Μεσαίωνα, γεννήθηκε τον 12ο αιώνα στην Πίζα της Τοσκάνα γι αυτό και
οι Ιταλοί τον λένε και Leonardo da Pisa.
Η Pisa απέχει από το χωριό Vinci μερικές
δεκάδες χιλιόμετρα και ο Leonardo da Pisa προηγήθηκε κατά
τρεις περίπου
αιώνες του Leonardo
da
Vinci,
ο οποίος θα κάνει την εμφάνισή του στον πλανήτη τον 15ο αιώνα. Και οι δύο τους πάντως ήταν Ιταλοί, «παιδιά της Τοσκάνα», όπως εξάλλου και ο Γαλιλαίος που
θα γεννηθεί έναν περίπου
αιώνα μετά τον Λεονάρντο ντα Βιντσι στην Πίζα.
Σε ένα ταξίδι που έκανα
πριν μερικά χρόνια οδηγώντας αυτοκίνητο
στην Autostrada
από την Φλωρεντία στην Πίζα, αναζητώντας τα ίχνη του Γαλιλαίου
και του Φιμπονάτσι , λίγο πριν το μέσο της διαδρομής είδα ξαφνικά την ταμπέλα «
προς Vinci»,
το σκέφτηκα για λίγο, ήταν εκτός
προγράμματος, και τελικά έστριψα.
Η στροφή με οδήγησε στο
χωριό του Λεονάρντο, σε μια σοβαρότερη γνωριμία μου με το έργο του και λίγο
αργότερο στο βιβλίο «Το φάντασμα του
Λεονάρντο » στις εκδόσεις Κάτοπτρο

Στους αιώνες που
ακολούθησαν οι άνθρωποι που ερευνούσαν τα πράγματα, με πρώτο τον Λεονάρντο ντα Βίντσι πρόσεξαν ότι η τα πέταλα στο άνθος του λουλουδιών αλλά
και τα φύλλα στον βλαστό διευθετούνται με βάση την ακολουθία Fibonacci
Στην
περίπτωση του ρόδου μια γωνία προσδιοριζόμενη από τον αριθμό φ της χρυσής τομής «χωρίζει» το ένα πέταλο από το άλλο .
Σε μοίρες είναι ίση με 360/φ, είναι
δηλαδή 222,5 μοίρες και η αντίστοιχη κυρτή γωνία ίση 137,5 μοίρες
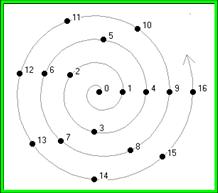 Τα
φύλλα τα μετράμε αρχίζοντας από ένα σημείο Χ και κάνοντας με το βλέμμα της
σκέψης μας περιστροφές κατά τη φορά του ρολογιού με ολοένα αυξανόμενη ακτίνα.
Τα
φύλλα τα μετράμε αρχίζοντας από ένα σημείο Χ και κάνοντας με το βλέμμα της
σκέψης μας περιστροφές κατά τη φορά του ρολογιού με ολοένα αυξανόμενη ακτίνα.
Από το σημείο Χ
στρεφόμενοι κατά 222.5 μοίρες συναντάμε την άκρη του φύλλου 1,
στη συνέχεια στρεφόμενοι
κατά την ίδια γωνία συναντάμε την άκρη του φύλλου 2 και αν συνεχίσουμε με τον  ίδιο
τρόπο θα συναντήσουμε καθένα από τα υπόλοιπα στο άκρο του.
ίδιο
τρόπο θα συναντήσουμε καθένα από τα υπόλοιπα στο άκρο του.
Η
γωνία την οποία έχουμε επιλέξει είναι το κλάσμα της γωνίας 360ο δια
του αριθμού φ και - δεδομένου ότι φ = 1,618- είναι περίπου ίση με 222.5 μοίρες.
|
Αριθμός φύλλων |
στροφές |
|
3 |
1 |
|
5 |
2 |
|
8 |
3 |
Παρατηρούμε ότι τα φύλλα
3 και 5 είναι σχετικά γειτονικά λίγο έξω από το σημείο Χ . Τα επόμενα γειτονικά
ακόμα πιο έξω από το σημείο Χ είναι τα φύλλα 8 και 13.
Το γεωμετρικό αυτό
μοντέλο για τη διάταξη των φύλλων δείχνει οι αριθμοί των φύλλων σε κάθε στήλη
είναι αριθμοί Fibonacci

Τελικά
εκείνη «μ’ αγαπά ;»
ή
εξαρτάται από το ξεφύλλισμα της μαργαρίτας;
 Σε
όλα σχεδόν τα άνθη, το πλήθος των πετάλων είναι ίσο με κάποιον από τους
αριθμούς της παράξενης ακολουθίας 3, 5, 8, 13, 21, 34, 55, 89.
Σε
όλα σχεδόν τα άνθη, το πλήθος των πετάλων είναι ίσο με κάποιον από τους
αριθμούς της παράξενης ακολουθίας 3, 5, 8, 13, 21, 34, 55, 89.
Βέβαια το παιχνίδι της
ζωής – προσδιοριζόμενο από την κληρονομικότητα
και από το περιβάλλον- είναι πολύ πιο περίπλοκο . Ωστόσο,
ορισμένα είδη, όπως η νεραγκούλα έχουν πάντα τον ίδιο αριθμό πετάλων. Τα
περισσότερα όμως έχουν αριθμό πετάλων που βρίσκεται «ΓΥΡΩ» από κάποιον αριθμό, αλλά
ο μέσος όρος είναι ένας ΑΡΙΘΜΟΣ Fibonacci
.
Ο κρίνος έχει ένα μόνο
πέταλο. Είναι αρκετά σπάνιο.
Το να έχει ένα άνθος 3
πέταλα είναι συνηθέστερο


Ακόμα πιο συχνά
εμφανίζεται το να έχει το άνθος 5 πέταλα.
 Αυτό συμβαίνει σε εκατοντάδες, τόσο άγρια
Αυτό συμβαίνει σε εκατοντάδες, τόσο άγρια
όσο και καλλιεργούμενα είδη.
Οι
κίτρινες μαργαρίτες που κάνουν την εμφάνισή τους στο Καλαμάκι έχουν 13 πέταλα.
Στο ξεφύλλισμα « Μ’ ΑΓΑΠΑ  – ΔΕΝ Μ’ ΑΓΑΠΑ» το ότι ΣΕ ΑΓΑΠΑ έχει σχεδόν
εξασφαλιστεί, ή τουλάχιστον, «παίζει» με
μεγάλες πιθανότητες.
– ΔΕΝ Μ’ ΑΓΑΠΑ» το ότι ΣΕ ΑΓΑΠΑ έχει σχεδόν
εξασφαλιστεί, ή τουλάχιστον, «παίζει» με
μεγάλες πιθανότητες.
Το
να έχει ένα άνθος 21 δεν είναι ασυνήθιστο. Οι άσπρες μαργαρίτες έχουν συνήθως
τόσα και στο ξεφύλλισμά τους, το ότι ΣΕ
ΑΓΑΠΑ, «παίζει» επίσης με μεγάλες πιθανότητες.
21 πέταλα έχουν και ορισμένοι κατιφέδες

 Το να έχει ένα άνθος – όπως το τριαντάφυλλο – 34 πέταλα είναι
επίσης αρκετά πιθανό να συμβεί.
Το να έχει ένα άνθος – όπως το τριαντάφυλλο – 34 πέταλα είναι
επίσης αρκετά πιθανό να συμβεί.
Η
καλέντουλα είναι ένα μόνο παράδειγμα
Από κει και πέρα μπορεί
ένα άνθος να έχει 55 πέταλα όπως ορισμένες μαργαρίτες ή και 89  πέταλα,
όπως τo
εκατόφυλλo
τριαντάφυλλo
που έκανε την εμφάνισή του στην Ευρώπη τον 17ο
αιώνα πλάσμα χειροπιαστό που ήλθε στον κόσμο μετά από επίμονες προσπάθειες
διασταυρώσεων
πέταλα,
όπως τo
εκατόφυλλo
τριαντάφυλλo
που έκανε την εμφάνισή του στην Ευρώπη τον 17ο
αιώνα πλάσμα χειροπιαστό που ήλθε στον κόσμο μετά από επίμονες προσπάθειες
διασταυρώσεων
των Ολλανδών κηπουρών
της εποχής
Ανδρέας
Ιωάννου Κασσέτας