Ανδρέας Ιωάννου Κασσέτας

3. Το 1842, ο Christian Doppler

α . Η σκέψη και η εξίσωση

Γεννημένος στο Ζάλτσμπουργκ της Αυστρίας, παιδί του 19^ου αιώνα, της γενιάς του Βικτόρ Ουγκώ του Λεντς και του Δαρβίνου, ο Κρίστιαν Ντόπλερ σπούδασε

Μαθηματικά, Φιλοσοφία, Αστρονομία και Μηχανική και έζησε 50 χρόνια.

Ήταν έτος 1842 κι εκείνος 40 περίπου ετών όταν με μία του δημοσίευση εστίασε την

προσοχή στο γεγονός ότι εφόσον ένας ακροατής κινείται σε σχέση με μία ηχητική πηγή

ο ήχος τον οποίο αντιλαμβάνεται έχει διαφορετικό ΥΨΟΣ από εκείνον που θα αντιλαμβανόταν από την ίδια πηγή χωρίς να υπάρχει σχετική κίνηση

Από τη σκοπιά της ακουστικής εμπειρίας αυτό που είναι μπορεί να διακρίνει το ανθρώπινο αυτί είναι το ΥΨΟΣ ( η οξύτητα ) του ήχου και ο ακροατής να αποφανθεί ότι ένας ήχος είναι υψηλότερος ή χαμηλότερος – πιο μπάσος – από έναν άλλο. Υπό αυτή την έννοια είναι ένα ΥΠΟΚΕΙΜΕΝΙΚΟ ΧΑΡΑΚΤΗΡΙΣΤΙΚΟ.

Την εποχή του Doppler ήταν γνωστό ότι η έννοια η οποία θα μπορούσε να ποσοτικοποιήσει – αντικειμενικά- την υποκειμενική μας αντίληψη για ύψος είναι η ΣΥΧΝΟΤΗΤΑ . Υψηλότερος κατά την αντίληψή μας ήχος , σημαίνει ήχος μεγαλύτερης ( υψηλότερης, όπως συνηθίζεται να λέγεται) συχνότητας.

Η ΣΥΧΝΟΤΗΤΑ είναι ποσοτική έννοια που περιγράφει «πόσες μεταβολές συμβαίνουν ανά δευτερόλεπτο» ανεξάρτητα από το εάν ο ήχος θα γίνει αντιληπτός από το σχετικό αισθητήριο. Υπό την έννοια αυτή μπορούμε να πούμε ότι είναι ένα ΑΝΤΙΚΕΙΜΕΝΙΚΟ ΧΑΡΑΚΤΗΡΙΣΤΙΚΟ

Ο Christian Dopper παρουσίασε μία και την εξίσωση που απαντούσε στο ερώτημα «πόσο αλλοιώνεται η συχνότητα ; ».

Σύμφωνα με αυτή η συχνότητα που αντιλαμβάνεται ο ακροατής είναι μεγαλύτερη εφόσον πλησιάζει την πηγή και μικρότερη εφόσον απομακρύνεται από αυτή.

β. Η εμπειρία. Ολλανδοί σαλπιγκτές στο βαγόνι

Δυο χρόνια μετά τη δημοσίευση του Doppler το φαινόμενο ελέγχθηκε από έναν Ολλανδό ερευνητή ο οποίος προσπάθησε να αποδείξει εμπειρικά ότι «κάτι τέτοιο» ήταν αδύνατον να συμβαίνει. Για τον σκοπό αυτό οργάνωσε στην Ολλανδία ένα από τα πιο «θεατρικά» πειράματα στην ιστορία της έρευνας.

Σαλπιγκτές χωρίστηκαν σε δύο ομάδες και τους ζητήθηκε να παίζουν τη νότα Μι-ύφεση.

Η μία ομάδα έπαιζε μέσα σε ανοικτό βαγόνι που το έσερνε αμαξοστοιχία σε μια πρόσφατα ανοιγμένη γραμμή στην περιοχή της Ουτρέχτης, ενώ η άλλη ομάδα έπαιζε στην αποβάθρα. Μια τρίτη ομάδα στην αποβάθρα ήταν μουσικοί με γυμνασμένο αυτί, οι οποίοι ήταν οι ακροατές.

Όταν και οι δύο ομάδες ήταν ακίνητες οι εξασκημένοι ακροατές αναγνώριζαν στους δύο ήχους το ίδιο ύψος, ενώ όταν το βαγόνι πλησίαζε, οι ασκημένοι

διαπίστωναν ότι ο Doppler είχε δίκιο.

Η νότα ακουγόταν υψηλότερη και γινόταν όλο και πιο ψηλή καθώς η ταχύτητα του βαγονιού μεγάλωνε. Όταν δε το βαγόνι απομακρυνόταν η νότα γινόταν πιο χαμηλή.

4. Επιστήμη και Τεχνολογία

α. Μετατόπιση στο ΕΡΥΘΡΟ

και Edwin Hubble

Στην ίδια αρχική δημοσίευση του 1842 , αποδεχόμενος την κυρίαρχη άποψη της εποχής ότι και το φως διαδίδεται με κύματα, ο Doppler αναφέρθηκε και στην αλλοίωση του χρώματος ενός φωτεινού σώματος εφόσον υφίσταται σχετική κίνηση φωτεινού αντικειμένου και παρατηρητή. Και αντικειμενικό χαρακτηριστικό για το χρώμα είναι η ΣΥΧΝΟΤΗΤΑ του φωτεινού κύματος .

Όπως και για τον ήχο, στην περίπτωση του φωτός η θεωρία του έβλεπε ότι εφόσον η φωτεινή πηγή απομακρύνεται από τον παρατηρητή η συχνότητα που γίνεται αντιληπτή είναι μικρότερη από εκείνη που θα διαπίστωνε ένας ακίνητος.

Και μικρότερη συχνότητα είναι μία «μετατόπιση προς το ερυθρό» επειδή το ερυθρό έχει τη μικρότερη συχνότητα από όλες τις ορατές ακτινοβολίες. Ωστόσο ο Doppler πρόβλεψε ότι η οπτική αυτή μετατόπιση θα μπορούσε να επιβεβαιωθεί εμπειρικά ΜΟΝΟ εφόσον η φωτεινή πηγή είχε ταχύτητα συγκρίσιμη με εκείνη των «φωτεινών κυμάτων».

Σε αντίθεση με τα ηχητικά κύματα η επαλήθευση για τα φωτεινά κύματα καθυστέρησε 25 περίπου χρόνια, όταν ο Doppler είχε φύγει από τη ζωή και ο αρκετά νεώτερός του Άγγλος αστρονόμος William Huggins κατάφερε να ανιχνεύσει τη λεγόμενη «μετατόπιση Doppler προς το ερυθρό» στο φάσμα του φωτός του άστρου Σείριος. Αυτό ήταν μια σοβαρή ένδειξη ότι ο Σείριος απομακρύνεται από τη Γη.

Στις αρχές του 20^ου αιώνα η εξίσωση του Doppler για την οπτική μετατόπιση τροποποιήθηκε για να εναρμονιστεί με την Ειδική Θεωρία της Σχετικότητας. Βέβαια η μετατόπιση στο ερυθρό εξακολουθούσε να σημαίνει ότι «το άστρο απομακρύνεται από τη Γη» – και η ενδεχόμενη μετατόπιση προς το μπλε ότι «πλησιάζει» - αλλά η εξίσωση που δίνει την τιμή της μετατόπισης θεωρείται πλέον διαφορετική από την αντίστοιχη για τον ήχο.

Οι σύμφωνα με την Ειδική Θεωρία της Σχετικότητας εξισώσεις του φαινομένου Doppler είναι

f_φ = f√c+υ)/√(c- υ) εφόσον η πηγή πλησιάζει τον παρατηρητή και

f_φ = f √c-υ)/√(c+ υ) εφόσον η πηγή απομακρύνεται από τον παρατηρητή

Σε αντίθεση με τον ήχο, στην περίπτωση του φωτός δεν εμφανίζεται η – ως προς τον αέρα - ταχύτητα του παρατηρητή και η – ως προς τον αέρα - ταχύτητα της πηγής, αλλά μόνο η σχετική ταχύτητα υ των δύο

Τη δεκαετία του 1920 ο Αμερικανός αστρονόμος Vesto Slipher, βασιζόμενος στη θεωρία Doppler, κατάφερε να μετρήσει τις ταχύτητες ενός πλήθους γαλαξιών οι περισσότεροι από τους οποίους έδειχναν « μετατόπιση στο ΕΡΥΘΡΟ» και άρχισε να εδραιώνεται η πεποίθηση ότι ΟΙ ΓΑΛΑΞΙΕΣ ΑΠΟΜΑΚΡΥΝΟΝΤΑΙ.

Ήταν η εποχή που έκανε την εμφάνισή του

στο προσκήνιο ο μεγαλύτερος αστρονόμος

του 20^ου αιώνα ο Αμερικανός Edwin Hubble

ο οποίος βασιζόμενος σε ένα τεράστιο

αριθμό μετρήσεων και στη θεωρία

για « γαλαξιακές μετατοπίσεις Doppler»

θα διατυπώσει τον νόμο για την απομάκρυνση

των Γαλαξιών η οποία λαμβάνει χώρα

με ταχύτητα ανάλογη προς την απόστασή τους.

Ο νόμος του Hubble θα σημαδέψει την εξέλιξη

των ιδεών για τη δομή του Σύμπάντος

ανοίγοντας ένα παράθυρο για το Big Bang .

β. Φαινόμενο Doppler

σε ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΚΥΜΑΤΑ

Το φαινόμενο Doppler εκδηλώνεται και σε ηλεκτρομαγνητικά κύματα, όπως είναι λόγου χάρη τα ραδιοκύματα. Η σχέση που το περιγράφει είναι ίδια με εκείνη για το φως

Ένα ραντάρ ακίνητο ως προς το έδαφος εκπέμπει ηλεκτρομαγνητικό κύμα το οποίο ανακλάται σε κινούμενο αυτοκίνητο και επιστρέφει στο ραντάρ με ελαφρώς διαφορετική συχνότητα. Με βάση τη μικρή αυτή διαφορά της συχνότητας η διάταξη μπορεί να υπολογίσει την ταχύτητα του αυτοκινήτου

γ. Φαινόμενο Doppler σε ΥΠΕΡΗΧΟΥΣ.

Η ταχύτητα ροής του αίματος

Δεν είναι καθόλου λίγοι οι μαθητές – αλλά και οι ενήλικοι - στους οποίους δημιουργείται εννοιακή σύγχυση ανάμεσα στις έννοιες

ΥΠΕΡΗΧΗΤΙΚΟ ΑΝΤΙΚΕΙΜΕΝΟ - αεροπλάνο- και ΥΠΕΡΗΧΟΣ.

Εκτιμούν ΣΩΣΤΑ ότι τα υπερηχητικά σκάφη είναι σκάφη που μπορούν να αναπτύσσουν ταχύτητα μεγαλύτερη από του ήχου, και εκτιμούν ΛΑΘΟΣ

ότι οι υπέρηχοι έχουν μεγαλύτερη ταχύτητα από εκείνη των ήχων.

Η ευθύνη, εκτός των άλλων, πρέπει να αποδοθεί και στη σχετική ένδεια της νεοελληνικής η οποία δεν έχει άλλη λύση από το να χρησιμοποιήσει την πρόθεση ΥΠΕΡ για δύο τόσο διαφορετικές έννοιες. Είναι χαρακτηριστικό ότι η αγγλική στη θέση του νεοελληνικού ΥΠΕΡ χρησιμοποιεί κατά περίπτωση το SUPER, το ULTRA και το HYPER.

Μια από τις συνέπειες είναι οι Έλληνες να χρησιμοποιούν αγγλικούς όρους λέγοντας το SUPERMARKET σουπερμάρκετ και τα τσιγάρα ULTRA LIGHT ούλτρα λάιτ. Στην περίπτωσή μας η αγγλική μιλάει για σκάφη SUPERSONICS τα οποία μεταφράζουμε υπερηχητικά και για κυματικές μορφές ULTRASOUNDS τις οποίες μεταφράζουμε υπέρηχους.

Οι ΥΠΕΡΗΧΟΙ είναι κυματικές οντότητες, διαδίδονται στον αέρα – και όχι μόνο- ως κύματα ελαστικότητας με την ΙΔΙΑ ΤΑΧΥΤΗΤΑ που διαδίδονται και οι ήχοι αλλά ξεχωρίζουν στο ζήτημα της ΣΥΧΝΟΤΗΤΑΣ. Το «ΥΠΕΡ» που τους κάνει να διακρίνονται από τους ήχους δεν είναι η ταχύτητά τους αλλά η μεγαλύτερη ( υψηλότερη ) συχνότητά τους Με δεδομένο ότι το κριτήριο για τους ήχους είναι το ΑΝΘΡΩΠΙΝΟ ΑΥΤΙ οι υπέρηχοι δεν μπορούν να ανιχνευτούν με την ανθρώπινη ακοή και αυτό σχετίζεται με τη πολύ υψηλή συχνότητά τους . Παράγονται τόσο στα «εργαστήρια» της φύσης όσο και στα εργαστήρια που έχουν δημιουργήσει οι άνθρωποι κυρίως με τεχνολογία του 20^ου αιώνα. Ενώ ως όριο για τους ήχους θεωρείται η συχνότητα 20000 Hz οι υπέρηχοι των εργαστηρίων του 20^ου αιώνα έχουν πολύ μεγαλύτερες . Το 2 MHz - 2.000.000 Hz - είναι συνήθης τιμή συχνότητας υπερήχων, ενώ είναι δυνατόν σήμερα να παράγονται υπέρηχοι και πάνω από 200 MHz

Οι υπέρηχοι εκδηλώνουν όλα τα κυματικού χαρακτήρα ΦΑΙΝΟΜΕΝΑ. Ανακλώνται, διαθλώνται, περιθλώνται, συμβάλλουν, εκδηλώνουν και φαινόμενο Doppler για το οποίο ισχύουν οι ίδιες εξισώσεις που ισχύουν και για τους ήχους. Με βάση το φαινόμενο Doppler μπορούμε να μετρήσουμε την ταχύτητα των ανθρώπινων ερυθρών αιμοσφαιρίων άρα και την ταχύτητα ροής του αίματος στα αιμοφόρα αγγεία.

Ανάκλαση σε κινητό εμπόδιο και φαινόμενο Doppler

Η ερώτηση. Σε μια ηχοκαρδιογραφία Doppler μία δέσμη υπερήχων συχνότητας f και ταχύτητας c ανακλάται σε κινητό εμπόδιο-αιμοσφαίριο το οποίο πλησιάζει προς το σημείο εκπομπής και ανίχνευσης. Κατά της επιστροφή της ανακλώμενης δέσμης στο σημείο εκπομπής ανιχνεύεται αύξηση της συχνότητας Δf .

Πώς μπορούμε να υπολογίσουμε την ταχύτητα του αιμοσφαιρίου ;

Η απάντηση . Σε κάθε περίπτωση η ανακλώμενη δέσμη είναι μια δέσμη που προέρχεται από το ΕΙΔΩΛΟ

Εάν ο ανακλαστήρας θεωρηθεί επίπεδος

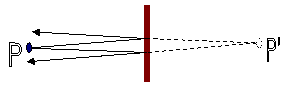το είδωλο θα είναι συμμετρικό ως προς

το σημείο Ρ από το οποίο εκπέμπεται η δέσμη.

Το Ρ εκτός από ακίνητο σημείο εκπομπής είναι

και το σημείο στο οποίο ανιχνεύεται

η ανακλώμενη δέσμη.

Εφόσον το εμπόδιο πλησιάζει προς το Ρ, με

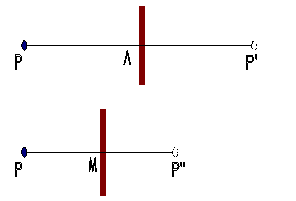ταχύτητα υ, αποδεικνύεται ότι

το συμμετρικό -ως προς τον ανακλαστήρα –

είδωλο Ρ’ κινείται προς την ίδια κατεύθυνση

με ταχύτητα 2υ.

Αν η αρχική απόσταση του ανακλαστήρα από το Ρ

είναι x και η τελική y , το είδωλο αρχικά απέχει

από το Ρ 2x και τελικά 2y. Η μετατόπιση συνεπώς

του ανακλαστήρα είναι x+y και, στο ίδιο χρονικό

διάστημα η μετατόπιση του ειδώλου είναι 2(x+y)

υ_ειδ = 2υ Το είδωλο πλησιάζει συνεπώς προς

τον ανιχνευτή με ταχύτητα 2υ και στον ακίνητο ανιχνευτή προσπίπτει κύμα

προερχόμενο από «πηγή» η οποία πλησιάζει με ταχύτητα 2υ.

Σύμφωνα με την εξίσωση Doppler

f_φ = fc/( c-2υ) Δf= fc/(c-2υ) –f Δf= 2fυ/(c-2υ) και με προσέγγιση Δf= 2fυ/c,

από την οποία υπολογίζουμε την ταχύτητα υ του εμποδίου/αιμοσφαιρίου

Και 13 ερωτήματα

Μία ηχητική πηγή εκπέμπει ηχητικά κύματα συχνότητας f στον αέρα ως προς τον οποίο η ταχύτητα διάδοσης του ήχου είναι υ, οπότε και το μήκος κύματος είναι λ= υ/f . Ένας ακροατής ήχων είναι είτε ακίνητος είτε κινείται ( ως προς τον αέρα άρα και ως προς το έδαφος ) έτσι ώστε η - ως προς έδαφος - ταχύτητά του να ανήκει συνεχώς στην ευθεία πηγή-ακροατής. Η πηγή των ήχων είναι είτε ακίνητη είτε κινείται ( ως προς έδαφος ) έτσι ώστε η -ως προς έδαφος - ταχύτητά της να ανήκει συνεχώς στην ευθεία πηγή- ακροατής. Εάν είναι υ_ηχφ, η ως προς τον ακροατή ταχύτητα του ηχητικού κύματος , λ_φ το μήκος κύματος το οποίο εκείνος αντιλαμβάνεται για το ηχητικό κύμα και fφ η συχνότητα την οποία εκείνος αντιλαμβάνεται για το ηχητικό κύμα με ποια από τα παρακάτω συμφωνείτε;

Με τα υ, υ_ηχφ, υ_Α και υ_π συμβολίζουμε τα μέτρα των αντίστοιχων ταχυτήτων υ η ταχύτητα του ηχητικού κύματος στον αέρα υ_ηχφ η ως προς τον ακροατή ταχύτητα του ηχητικού κύματος, υ_Α η - ως προς έδαφος – ταχύτητα του ακροατή και υ_π η - ως προς έδαφος – ταχύτητα της πηγής

Με ποια από τα παρακάτω συμφωνείτε;

( αποδέχεστε δηλαδή ή δεν αποδέχεστε ως ΣΩΣΤΗ ολόκληρη την τριάδα των σχέσεων )

α. Εάν ο ακροατής απομακρύνεται από την ακίνητη πηγή

λ_φ = λ υ_ηχφ = υ + υ_Α fφ < f ( αποδέχομαι ή δεν αποδέχομαι ως ΣΩΣΤΗ ολόκληρη την τριάδα των σχέσεων )

λ_φ = λ υ_ηχφ = υ - υ_Α fφ < f

λ_φ > λ υ_ηχφ = υ fφ < f

β. Εάν ο ακροατής πλησιάζει την ακίνητη πηγή

λ_φ = λ υ_ηχφ = υ + υ_Α fφ > f

λ_φ = λ, υ_ηχφ = υ - υ_Α fφ > f

λ_φ > λ υ_ηχφ, = υ fφ > f

γ. Εάν λ_φ = λ η πηγή είναι οπωσδήποτε ακίνητη, ανεξάρτητα από το εάν κινείται ο ακροατής

δ. Εάν η πηγή πλησιάζει τον ακίνητο ακροατή

λ_φ = λ υ_ηχφ = υ + υ_Α fφ > f

λ_φ = λ- υ_π /f υ_ηχφ = υ fφ > f

ε . Εάν η πηγή απομακρύνεται από τον ακίνητο ακροατή

λ_φ = λ υ_ηχφ = υ + υ_Α fφ < f

λ_φ = λ + υ_π /f υ_ηχφ = υ fφ = fυ / (υ+υ_π)

στ. Εάν υ_ηχφ = υ ο ακροατής είναι ακίνητος ανεξάρτητα από το εάν κινείται η πηγή

ζ. Εάν η πηγή και ο ακροατής κινούνται προς αντίθετες κατευθύνσεις και απομακρύνονται

λ_φ = λ+ υ_π /f υ_ηχφ = υ - υ_Α fφ = f(υ + υ_Α) / (υ- υ_π)

λ_φ = λ υ_ηχφ = υ + υ_Α fφ < f

η. Εάν η πηγή και ο ακροατής πλησιάζουν κινούμενοι με προς αντίθετες κατευθύνσεις

λ_φ = λ+ υ_π /f υ_ηχφ = υ fφ > f

λ_φ = λ- υ_π /f υ_ηχφ = υ + υ_Α fφ > f

θ. Εάν ο ακροατής κινείται στην ίδια κατεύθυνση με εκείνη της διάδοσης του ήχου

υ_ηχφ = υ - υ_Α υ_ηχφ = υ + υ_Α υ_ηχφ = υ

ι. Εάν η πηγή κινείται στην ίδια κατεύθυνση με εκείνη της διάδοσης του ήχου

λ_φ = λ+ υ_π /f λ_φ = λ- υ_π /f λ_φ = λ

ια. Εάν ο ακροατής κινείται σε αντίθετη κατεύθυνση από εκείνη της διάδοσης του ήχου

υ_ηχφ = υ + υ_Α ανεξάρτητα από το «τι συμβαίνει με την πηγή»

ιβ. Εάν η πηγή κινείται σε αντίθετη κατεύθυνση από εκείνη της διάδοσης του ήχου

λ_φ = λ+ υ_π /f ανεξάρτητα από το «τι συμβαίνει με τον ακροατή»

ιγ. Εάν η πηγή και ο ακροατής κινούνται προς την ίδια κατεύθυνση

με προηγούμενο τον ακροατή και με ίσες ταχύτητες ως προς το έδαφος

λ_φ = λ - υ_π /f υ_ηχφ = υ - υ_Α fφ = f

λ_φ = λ υ_ηχφ = υ fφ = f