Η στροφορμή μιας σφαίρας

Η στροφορμή μιας στρεφόμενης περί άξονα συμμετρίας ομογενούς σφαίρας είναι ίδια ως προς οποιοδήποτε σημείο ;

Αν θεωρήσουμε ένα σύστημα δύο υλικών σημείων σε απόσταση d με ίσες μάζες το οποίο στρέφεται περί άξονα. Καθένα τους εκτελεί κυκλική κίνηση ακτίνας r= d/2 με ορμή mυ. Η ως προς το κέντρο 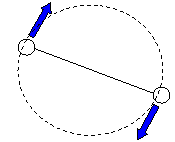μάζας στροφορμή του ενός είναι mυr, όσο και του άλλου άρα η στροφορμή του συστήματος είναι ίση με mυd και έχει τη φορά της γωνιακής ταχύτητας. Εύκολα αποδεικνύεται ότι

« η ΣΤΡΟΦΟΡΜΗ του συστήματος ως προς το κέντρο μάζας είναι ίση με τη ΣΤΡΟΦΟΡΜΗ ως προς οποιοδήποτε γεωμετρικό σημείο ».

Συμβαίνει δηλαδή κάτι παρόμοιο με αυτό που συμβαίνει με ένα ζεύγος δυνάμεων και με τη ροπή του ζεύγους. Εξάλλου η στροφορμή είναι ροπή της ορμής.

Μία ομογενής σφαίρα στρεφόμενη περί άξονα που περνά από το κέντρο της μπορεί να θεωρηθεί ως σύνολο από ζευγάρια υλικών σημείων με αντίθετες ορμές με αποτέλεσμα η ως προς το κέντρο της σφαίρας ΣΤΡΟΦΟΡΜΗ ΤΗΣ ΣΤΡΕΦΟΜΕΝΗΣ με αυτόν τον τρόπο ΣΦΑΙΡΑΣ είναι ίση με τη ΣΤΡΟΦΟΡΜΗ της ως προς οποιοδήποτε γεωμετρικό σημείο». Αυτό σημαίνει ότι κάθε στρεφόμενη περί άξονα συμμετρίας ομογενής σφαίρα ΕΧΕΙ ορισμένη στροφορμή, 2/5mR²ω, ανεξάρτητα από το σημείο στο οποίο θα αναφέρεται. Γι αυτό και οι φυσικοί όταν μιλούν για στρεφόμενη περί άξονα συμμετρίας σφαίρα λένε « η στροφορμή της ».

Η στροφορμή μιας κυλιόμενης ομογενούς σφαίρας είναι ίδια ως προς οποιοδήποτε σημείο ;

Αυτό όμως δεν συμβαίνει όταν μία σφαίρα κυλίεται χωρίς να ολισθαίνει.

Σε αυτή την περίπτωση η τιμή της στροφορμής διαφοροποιείται εάν αναφερόμαστε σε διαφορετικό γεωμετρικό σημείο

Η ως προς το κέντρο μάζας ( Κ ) στροφορμή είναι ίση με 2/5mR ²ω και δεδομένου ότι υ_cm = ω R είναι τελικά L = 2/5mυ_cmR και είναι ίση με τη στροφορμή που θα είχε εάν στρεφόταν περί άξονα συμμετρίας με γωνιακή ταχύτητα ω. Εξάλλου εάν αναλύσουμε την κίνηση σε μεταφορά και περιστροφή περί άξονα συμμετρίας, η λόγω της μεταφορικής κίνησης στροφορμή ως προς Κ είναι μηδέν.

Για το ίδιο φαινόμενο η ως προς το σημείο επαφής Σ με το έδαφος στροφορμή της σφαίρας είναι διαφορετική. Αυτή μπορεί να προσδιοριστεί

α. Εάν αναλύσουμε την κύλιση σε μεταφορά και περιστροφή περί Κ . Η λόγω μεταφορικής κίνησης στροφορμή της ως προς Σ είναι mυ_cmR και η λόγω στροφικής κίνησης περί άξονα συμμετρίας είναι 2/5mυ_cmR, οπότε η στροφορμή της θα είναι mυ_cmR + 2/5mυ_cmR = 7/5 mυ_cmR

β. Εάν θεωρήσουμε την κύλιση ως στιγμιαία στροφική κίνηση περί άξονα που περνά από το σημείο επαφής Σ, η στροφορμή της θα είναι Ι_Σω = (Ι_cm+ mR² )ω = 7/5mR²ω = 7/5 mυ_cmR.

Ανδρέας Ιωάννου Κασσέτας