η ΚΑΤΑΣΤΑΤΙΚΗ ΕΞΙΣΩΣΗ ΤΩΝ
ΑΕΡΙΩΝ
και οι δρόμοι που
οδήγησαν στην οικοδόμησή της
![]()
Κατά τη δεκαετία
του 1660, ο Ιρλανδός Robert Boyle, εργάζεται ερευνητικά στην Αγγλία, και
έχει ήδη γίνει αποδεκτός ως ένας από τους σημαντικότερους ερευνητές της γενιάς
του. Το 1662 , είναι 33 ετών, όταν
διαπιστώνει ερευνητικά ότι κατά την εκτόνωση του ΑΕΡΑ ,

καθώς αυξάνεται ο όγκος
του , η πίεση του ελαττώνεται - όχι με τυχαίο τρόπο αλλά - έτσι ώστε η τιμή του
να είναι αντιστρόφως ανάλογη του
όγκου, ή, με άλλα λόγια, ότι το «γινόμενο της πίεσης του αέρα επί τον όγκο του να διατηρείται σταθερό» .
|
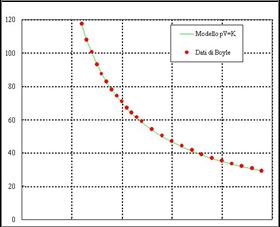
Διάγραμμα
με τα πειραματικά δεδομένα
του Boyle Την
πίεση του αέρα τη μετράει με το ύψος στήλης υδραργύρου και τον όγκο σε κυβικά
εκατοστά |
|
Το ίδιο διαπιστώνει και
κατά τη συμπίεση του αέρα και οδηγείται
έτσι στον πρώτο πειραματικό νόμο γι αυτά
τα φαινόμενα.
Στην εργασία του
χρησιμοποιεί δύο όμοια δοχεία και μία βαλβίδα. Αρχικά ο αέρας βρίσκεται μόνο
στο ένα δοχείο και η πίεσή του μετριέται με ύψος στήλης υδραργύρου. Στη συνέχει
ανοίγει τη βαλβίδα ο αέρας καταλαμβάνει διπλάσιο
όγκο και
με το νέα ύψος της υδραργυρικής στήλης διαπιστώνεται ότι η πίεση είναι μισή από την προηγούμενη
Δεκατέσσερα
χρόνια αργότερα, το έτος δηλαδή 1676, ο
Γάλλος ιερέας και ερευνητής Edmé Mariotte, τότε 56 ετών, αγνοώντας την έρευνα του Boyle, καταλήγει πειραματικά στα ίδια
συμπεράσματα αλλά αποδίδει έμφαση σε ένα στοιχείο το οποίο είχε

 αγνοήσει ο Boyle και συγκεκριμένα στο
γεγονός ότι
αγνοήσει ο Boyle και συγκεκριμένα στο
γεγονός ότι
για να ισχύει το pV = σταθερό πρέπει, κατά τη διάρκεια της
συμπίεσης, η ΘΕΡΜΟΚΡΑΣΙΑ του αέρα να είναι
ΣΤΑΘΕΡΗ.
Την εποχή εκείνη δεν έχει ανακαλυφθεί το
ΘΕΡΜΟΜΕΤΡΟ αλλά οι ερευνητές χρησιμοποιούν θερμοσκόπιο με το οποίο δεν
μπορούν να γνωρίζουν «πόση είναι η θερμοκρασία» είναι όμως σε θέση να
διαπιστώνουν εάν «η θερμοκρασία ενός σώματος έχει αλλάξει ή διατηρείται
σταθερή».
Είναι
χαρακτηριστικό ότι τόσο ο Μπόιλ όσο και ο Μαριότ πειραματίζονται μόνο με ΑΕΡΑ.
Η σημαντική ΙΔΕΑ ότι , εκτός από τον
αέρα
«υπάρχουν και άλλα ΑΕΡΙΑ σώματα» έκανε την εμφάνισή της ένα περίπου αιώνα
αργότερα.
Το
φαινόμενο θα χαρακτηριστεί σε γλώσσα αγγλική isothermal process, στα γαλλικά processus isotherme
και στaν ελληνικά ΙΣΟΘΕΡΜΗ
ΜΕΤΑΒΟΛΗ. Στις γαλλόφωνες χώρες ,
ο νόμος θα λέγεται Loi
de
Mariotte, στις αγγλόφωνες χώρες Boyle Low
, ενώ οι Ισπανόφωνοι μιλούν για Ley
de
Boyle-Mariotte.
Στην ελληνική βιβλιογραφία εμφανίζεται σπανιότερα ως νόμος Boyle-Mariotte
και συχνότερα ως νόμος Boyle.
![]()
Στα τέλη του 17ου αιώνα εμφανίζεται η ΙΔΕΑ για ένα όργανο με
ΥΓΡΟ το οποίο θα μπορούσε να μετράει τη θερμοκρασία βασιζόμενο στο φαινόμενο
ΔΙΑΣΤΟΛΗ ΤΟΥ ΥΓΡΟΥ. Αρχικά χρησιμοποιείται το νερό, αργότερα το κρασί και το
χρωματισμένο οινόπνευμα. Η σκέψη να χρησιμοποιηθεί υδράργυρος υλοποιήθηκε μόνο
το 1721 από τον Γερμανό Daniel Fahrenheit που
μας έδωσε το πρώτο θερμόμετρο με τη σύγχρονη έννοια του όρου. Δύο περίπου
δεκαετίες αργότερα κάνει την εμφάνισή του στο προσκήνιο ο Σουηδός Anders Celsius, οποίος θα καταλήξει τελικά
να προτείνει τη θερμοκρασιακή κλίμακα που χρησιμοποιούμε και σήμερα

Τη δεκαετία του
1780, παραμονές της Γαλλικής
Επανάστασης, οι Γάλλοι ερευνητές διαθέτουν
ΘΕΡΜΟΜΕΤΡΟ και ΜΑΝΟΜΕΤΡΟ
αλλά
και την πεποίθηση των χημικών «εκτός από τον αέρα υπάρχουν πολλών μορφών ΑΕΡΙΑ
διαφορετικά » .
Χρησιμοποιώντας θερμόμετρο,
μανόμετρο και ογκομετρικές διατάξεις ο Jacques Charles
- Ζακ Σαρλ - γύρω στο 1787 , δυο χρόνια πριν ξεσπάσει η
Επανάσταση - αφού είχε ήδη κατασκευάσει αερόστατο με υδρογόνο - ερευνά
τη συμπεριφορά του αέρα κατά τη θέρμανσή του και συγκεκριμένα το φαινόμενο ΙΣΟΒΑΡΗΣ ΘΕΡΜΑΝΣΗ του αέρα το οποίο αναφέρεται
και ως ΔΙΑΣΤΟΛΗ του αέρα υπό σταθερή πίεση.
Οι μετρήσεις είχαν οδηγήσει σε συμπεράσματα για μια ΑΝΑΛΟΓΙΑ
ανάμεσα στην αύξηση της θερμοκρασίας και στην αντίστοιχη αύξηση του όγκου τα
οποία μπορούν να περιγραφούν με την ΔV = V0αΔθ με α
= 1/273 ανά βαθμό.
Επανέλαβε τις πειραματικές μετρήσεις και με άλλα αέρια
που δεν ήταν αέρας για να διαπιστώσει το
, ιδιαίτερα ΕΝΤΥΠΩΣΙΑΚΟ ότι
η – περίπου - κατά 1/273 ΑΥΞΗΣΗ του όγκου του αέρα
φαινόταν να ισχύει ΓΙΑ ΟΠΟΙΟΔΗΠΟΤΕ ΑΕΡΙΟ.
Την ίδια εποχή
ερευνώντας και τις συνέπειες της θέρμανσης του αέρα σε «κλειστό δοχείο –
ΙΣΟΧΩΡΗ ΘΕΡΜΑΝΣΗ - διαπίστωσε ότι και η αύξηση της πίεσης είναι ΑΝΑΛΟΓΗ προς την αύξηση της θερμοκρασίας και μάλιστα
για κάθε βαθμό αύξησης της θερμοκρασίας η πίεση αυξάνεται κατά το 1/273 της προηγούμενης τιμής της
καθώς και ότι η κατά το 1/273 ΑΥΞΗΣΗ της πίεσης ανά βαθμό ισχύει ΓΙΑ
ΟΠΟΙΟΔΗΠΟΤΕ ΑΕΡΙΟ. Η σχετική αναλογία
μπορεί να περιγραφεί με τη σχέση ΔΡ
= Ρ0αΔθ
Βέβαια 60 περίπου χρόνια αργότερα, το 1848,
ο Άγγλος λόρδος Κέλβιν - βασιζόμενος στον συντελεστή α = 1/273 grad-1 -
πρότεινε την λεγόμενη «απόλυτη
κλίμακα» θερμοκρασίας.
Με βάση αυτή την πρόταση η σχέση ΔV = V0αΔθ μετασχηματίζεται στην
V = V0 Τ/ Τ0 και η σχέση
ΔΡ = Ρ0αΔθ Ρ =
Ρ0(1+ αθ ) μετασχηματίζεται
στην Ρ = Ρ0 Τ/Τ0

Δώδεκα χρόνια αργότερα και ενώ η
Γαλλία είναι «Γαλλία του Ναπολέοντα», ένας νεαρός Γάλλος χημικός κάνει
παρόμοιες μετρήσεις με μεγαλύτερη ακρίβεια και σε περισσότερα αέρια. Με τον Berthollet και
τον LaPlace, να τον ενθαρρύνουν, εκείνος ετών 23, κάνει την ακριβέστερη μέχρι τότε έρευνα στην ΙΣΟΒΑΡΗ θέρμανση και τη συνεπαγόμενη ΔΙΑΣΤΟΛΗ των
αερίων και στην ΙΣΟΧΩΡΗ θέρμανσή τους. Είναι χειμώνας του 1801-2
, είναι Παρίσι κι εκείνος, ο JOSEPH LOUIS GAY-LUSSAC - Ζοζέφ Λουί Γκε Λυσάκ - θα δημοσιεύσει την εργασία του αλλά και θα ομολογήσει γραπτώς ότι πριν
δεκαπέντε χρόνια, παραμονές της Γαλλικής Επανάστασης ο Ζακ Σαρλ είχε
οδηγηθεί στα ίδια ακριβώς συμπεράσματα αλλά δεν τα δημοσίευσε ποτέ.
![]()
Το 1811 o Amedeo Avogadro έκανε την υπόθεση ( Υπόθεση Avogadro ) ότι
«ίσοι
όγκοι αερίου, στις ίδιες συνθήκες p,T,
έχουν τον ίδιο αριθμό moles»
Η ιδέα του οδήγησε στη διαπίστωση ότι
«σε κανονικές συνθήκες - p = 1 atm, T = 273 K - το ένα mole οποιουδήποτε αερίου
είχε όγκο 22,4 λίτρα ( Vm).
Η Υπόθεση του Avogadro, μολονότι καθυστέρησε ιδιαίτερα να γίνει αποδεκτή από του χημικούς,
απετέλεσε ένα βασικό θεμέλιο τόσο για τη συγκρότηση της Ατομικής Θεωρίας – πάνω
στην οποία δομήθηκε η Χημεία - όσο και για τη διαμόρφωση της λεγόμενης
Κινητικής Θεωρίας των Αερίων, η οποία θεμελίωσε τη Θερμοδυναμική

Το 1834, ο Γάλλος μηχανικός Émile Clapeyron θα
συνδυάσει τους τρεις νόμους των αερίων με την Υπόθεση Avogadro και θα προτείνει την
ΚΑΤΑΣΤΑΤΙΚΗ ΕΞΙΣΩΣΗ.
Υποθέτουμε ότι διαθέτουμε ένα mole
αερίου σε κανονικές συνθήκες, δηλαδή πίεσης Ρ0 = 1 atm και
θερμοκρασίας 00 Κελσίου. Ο όγκος του αερίου σύμφωνα με την υπόθεση Avogadro, θα είναι V0 = nVm.
Αν προκαλέσουμε συμπίεση του αερίου
σε μια τυχαία τιμή πίεσης Ρ1 και όγκου V1 , σύμφωνα με τον νόμο Boyle θα είναι Ρ0 V0 = Ρ1V1. Αν στη συνέχεια θερμάνουμε το αέριο,
υπό σταθερό όγκο, μέχρι να αποκτήσει μια τυχαία θερμοκρασία θ, οπότε η πίεση του έχει αυξηθεί
σε Ρ και ο όγκος του θα είναι V = V1
, σύμφωνα με τον νόμο Gay Lussac- Charles , θα είναι Ρ = Ρ1V( 1+ αθ).
Από τις εξισώσεις
V0 = nVm Ρ0V0 = Ρ1V1 V = V1
Ρ = Ρ1V( 1+ αθ) α
= 1/273 ανά βαθμό
προκύπτει ότι
ΡV = nΡ0Vm (273 +θ)/273.
Η ποσότητα Ρ0Vm/273 έχει μια τιμή ανεξάρτητη από το
είδος του αερίου. Αν τη συμβολίσουμε με το γράμμα R θα είναι ΡV = nR(273 +θ)
Στο ίδιο
αποτέλεσμα θα καταλήξουμε εάν,
ξεκινώντας από τις αρχικές κανονικές συνθήκες - αντί για ισόθερμη
συμπίεση και στη συνέχεια ισόχωρη θέρμανση - θεωρήσουμε μία ισοβαρή ψύξη και
στη συνέχεια μια ισόθερμη εκτόνωση, είτε
ένα οποιοδήποτε «ζευγάρι τέτοιων μεταβολών» . Μπορούμε να συμπεράνουμε ότι σε οποιαδήποτε κατάσταση πίεσης, όγκου και θερμοκρασίας βρεθεί ένα
αέριο θα ισχύει ΡV = nR(273 +θ).
Είναι η
καταστατική εξίσωση των αερίων.
![]()
Σε επίπεδο πειραματικής έρευνας
υπέβαλαν τα διάφορα γνωστά αέρια σε «ανάκριση» για να ερευνήσουν κατά πόσον καθένα από αυτά, σε μια τυχαία
κατάσταση, υπακούει στην καταστατική. Διαπιστώθηκε ότι
α. Κανένα αέριο δεν υπακούει απόλυτα
στην καταστατική
β. Όλα τα αέρια εφόσον βρίσκονται σε
κατάσταση μακριά της από τις συνθήκες υγροποίησής τους παρουσίαζαν μία
ικανοποιητική προσέγγιση υπακοής στην καταστατική εξίσωση.
Την ίδια εκείνη εποχή εμφανίστηκε και
η ιδέα για το «ΙΔΑΝΙΚΟ αέριο», ένα μοντέλο αερίου το οποίο υπακούει απόλυτα
στην καταστατική. Η σχετική εξίσωση πήρε τελικά το όνομα
«Καταστατική
εξίσωση των ιδανικών αερίων»
Παράλληλα το μοντέλο «ΙΔΑΝΙΚΟ αέριο»
συνδέθηκε και με τις θεωρίες για ένα Μικρόκοσμο της ύλης – συγκεκριμένα με την
Κινητική Θεωρία των Αερίων και τέθηκε το ερώτημα «πώς πρέπει να είναι η δομή
της ύλης ενός αερίου σε επίπεδο Μικρόκοσμου ώστε σε επίπεδο Μακρόκοσμου να
υπακούει στην Καταστατική, να είναι, με άλλα λόγια, ΙΔΑΝΙΚΟ ;»

Το 1848, ο
Άγγλος William Thomson, τότε 24 ετών, δημοσιεύει
το On an Absolute Thermometric Scaleστο οποίο προτείνει τη λεγόμενη ΑΠΟΛΥΤΗ
ΚΛΙΜΑΚΑ ΘΕΡΜΟΚΡΑΣΙΩΝ με το απόλυτο μηδέν. Το ΑΠΌΛΥΤΟ  ΜΗΔΕΝ της κλίμακας θα συνδεθεί τόσο με
τις θεωρίες Μικρόκοσμου – Κινητική Θεωρία των Αερίων – όσο και με την
πειραματική έρευνα. Συγκεκριμένα το βασικό στοιχείο που οδήγησε στην ιδέα για
την απόλυτη θερμοκρασία ήταν το πειραματικό δεδομένο του Charles και Gay Lussac ότι κατά την ψύξη ενός αερίου «η ελάττωση του όγκου κατά 1/273 ισχύει για όλα τα
αέρια». Μία οποιαδήποτε μεταβολή θερμοκρασίας στην απόλυτη κλίμακα είναι ΙΣΗ με
την αντίστοιχη μεταβολή στην κλίμακα Κελσίου, αλλά μια θερμοκρασία θ στην
κλίμακα Κελσίου αντιστοιχεί σε (273+θ) περίπου
στην απόλυτη κλίμακα, για την
ακρίβεια 273,15+θ.
ΜΗΔΕΝ της κλίμακας θα συνδεθεί τόσο με
τις θεωρίες Μικρόκοσμου – Κινητική Θεωρία των Αερίων – όσο και με την
πειραματική έρευνα. Συγκεκριμένα το βασικό στοιχείο που οδήγησε στην ιδέα για
την απόλυτη θερμοκρασία ήταν το πειραματικό δεδομένο του Charles και Gay Lussac ότι κατά την ψύξη ενός αερίου «η ελάττωση του όγκου κατά 1/273 ισχύει για όλα τα
αέρια». Μία οποιαδήποτε μεταβολή θερμοκρασίας στην απόλυτη κλίμακα είναι ΙΣΗ με
την αντίστοιχη μεταβολή στην κλίμακα Κελσίου, αλλά μια θερμοκρασία θ στην
κλίμακα Κελσίου αντιστοιχεί σε (273+θ) περίπου
στην απόλυτη κλίμακα, για την
ακρίβεια 273,15+θ.
Με βάση την απόλυτη κλίμακα,
η Καταστατική εξίσωση των ιδανικών αερίων πήρε την τελική της μορφή
ΡV = nRΤ
Μερικές δεκαετίες αργότερα, ο William Thomson θα λέγεται και λόρδος
KELVIN και η
κλίμακα θα χαρακτηρίζεται κλίμακα Κέλβιν.
Νόμος
Μπόιλ και Μαριότ ( ΑΓΓΛΙΑ, 1660, ΓΑΛΛΙΑ
1676) + Υδραργυρικό θερμόμετρο (Φαρενάιτ ΓΕΡΜΑΝΙΑ 1721) + Κλίμακα Κελσίου (
ΣΟΥΗΔΙΑ 1743)
+
Νόμοι Σαρλ και Γκέ Λυσάκ ( ΓΑΛΛΙΑ 1787
και 1802)
+
Υπόθεση Αβογκάντρο ( ΙΤΑΛΙΑ 1811 ) + Σύνθεση Κλαπεϊρόν ( ΓΑΛΛΙΑ
1834)
+
απόλυτη θερμοκρασία Κέλβιν ( ΑΓΓΛΙΑ 1848) =
ΚΑΤΑΣΤΑΤΙΚΗ ΕΞΙΣΩΣΗ .
Μια
ευρωπαϊκή εννοιακή οικοδόμηση που χρειάστηκε 200 περίπου χρόνια
Ανδρέας Ιωάννου Κασσέτας
.