Ανδρέας Ιωάννου Κασσέτας

Σύνθεση αρμονικών ταλαντώσεων

Τα μαθητικά «ΟΧΙ στην ΑΠΟΣΤΗΘΙΣΗ».

ΕΠΕΙΣΟΔΙΟ 1

Μαθητής : Στη σύνθεση δύο αρμονικών ταλαντώσεων με ίσες συχνότητες γράψατε στον πίνακα την εξίσωση

Α² = Α₁²+ Α₂² + 2Α₁Α₂συνφ

Τη βρήκαμε και στο σχολικό βιβλίο και καταλάβαμε ότι πρέπει να την αποστηθίσουμε.

Είναι και η άλλη, η ακόμα χειρότερη, η εφθ = δεν θυμάμαι πόσο . . . .. .. . ..

Μας λέγατε όμως τις προάλλες ότι η Φυσική δεν πρέπει να την αποστηθίζουμε

αλλά να την καταλαβαίνουμε.

Δεν υπάρχουν άλλοι τρόποι να προσδιορίζουμε μια σύνθετη ταλάντωση ;

Καθηγητής : Υπάρχουν και άλλοι τρόποι που δεν χρειάζονται ΑΠΟΣΤΗΘΙΣΗ.

Οι δύο ταλαντώσεις έχουν ίδια διεύθυνση, ίσες συχνότητες και κοινή θέση ισορροπίας x₁= A₁ημ(ωt+φ₁) x₂=A₂ημ(ωt+φ₂)

Ξεκινάμε με αυτό που ισχύει στη σύνθετη κίνηση, με βάση την αρχή της επαλληλίας

x = x₁+x₂

A₁ημ(ωt+φ₁) + A₂ημ(ωt+φ₂) Αημ(ωt+φ₁+θ)

Για t=0 ισχύει A₁ημφ₁ + A₂ημφ₂ = Αημ(φ₁+θ)

Για t=T/4 ισχύει A₁συνφ₁ + A₂ συνφ₂ = Ασυν(φ₁+θ)

Από τις δύο αυτές σχέσεις μπορούμε να υπολογίσουμε

1. το πλάτος Α της σύνθετης κίνησης αρκεί να υψώσουμε και τα δύο μέλη στο τετράγωνο και προσθέσουμε κατά μέλη Α² = . . . . .

2. Την τιμή της θ εάν διαιρέσουμε κατά μέλη οπότε εφ(φ₁+θ) =

Μαθητής : Καλό . . εμένα μου άρεσε . . . Ίσως βέβαια το «να αποστηθίζω»

μου προσφέρει μια σιγουριά αλλά με τσαντίζει . . .

ΕΠΕΙΣΟΔΙΟ

Μαθήτρια : - Κύριε . . . . η εξίσωση που μας γράφετε Α = √Α₁²+ Α₂² + 2Α₁Α₂συνφ

για τη σύνθεση δύο ταλαντώσεων μου θυμίζει μια εξίσωση που μας είχε γράψει ο καθηγητής

στην Α΄ Λυκείου για τη ΣΥΝΙΣΤΑΜΕΝΗ δύο δυνάμεων.

Αλλά και η άλλη εξίσωση εφθ = . . .. κάτι μου θυμίζει

Υπάρχει κάποια σχέση ανάμεσα στα φαινόμενα ΣΥΝΘΕΤΗ ΤΑΛΑΝΤΩΣΗ και στον υπολογισμό της συνισταμένης δύο δυνάμεων ;.

Καθηγητής : Πολύ καλή η παρατήρηση.

Για να συνθέσω δύο ταλαντώσεις

x₁ = A₁ημ(ωt+φ₁) και x₂ = A₂ημ(ωt+φ₂) με φ₂ > φ₁

μπορώ να ακολουθήσω την παρακάτω πρακτική

α. Σχεδιάζω ένα διάνυσμα μέτρου Α₁

β. Σχεδιάζω και ένα διάνυσμα μέτρου Α₂

έτσι ώστε η μεταξύ τους γωνία να είναι φ₂-φ₁

Βάζω αυτό που αντιστοιχεί στη μεγαλύτερη φάση έτσι ώστε να προηγείται κατά μία φορά περιστροφής

αντίθετη από εκείνη των δεικτών του ρολογιού και

γ. προσδιορίζω τη συνισταμένη τους Α

Το μέτρο της θα είναι το πλάτος της σύνθετης ταλάντωσης

η δε γωνία θ των διανυσμάτων Α και Α₁ θα είναι η διαφορά φάσης

της σύνθετης από την πρώτη

x = Aημ(ωt+φ₁+θ)

η δε γωνία των διανυσμάτων Α₂ και Α είναι η διαφορά φάσης

της δεύτερης ταλάντωσης από τη σύνθετη.

Μαθήτρια : - Με όλο τον σεβασμό αλλά αυτό που κάνετε είναι αυθαίρετο όσο και ο ΤΥΠΟΣ

Α = √Α₁²+ Α₂² + 2Α₁Α₂συνφ τον οποίο μας σερβίρει το σχολικό βιβλίο χωρίς καμία διευκρίνιση

Καθηγητής : Δεν έχεις άδικο. Εγώ σας παρουσίασα μια τεχνική για να βρίσκετε το πλάτος και τη φάση της σύνθετης ταλάντωσης. Ωστόσο δεν είναι αυθαίρετο.

Θα επιχειρήσω να το δικαιολογήσω χωρίς να απαιτήσω να το μάθετε και να σας αξιολογήσω πάνω σ’ αυτό. Είναι λίγο δύσκολο αλλά εάν προσέξετε θα κατανοήσετε τουλάχιστον τη λογική στην οποία βασίζεται η σχετική πρόταση.

Στη σύνθετη ταλάντωση στην οποία αναφερθήκαμε για την απομάκρυνση ισχύει

x = A₁ημ(ωt+φ₁) + A₂ημ(ωt+φ₂)

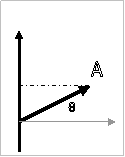
Μία αλγεβρική ποσότητα όπως η Αημθ μπορούμε να «φανταστούμε» και ως τιμή της ΠΡΟΒΟΛΗΣ ενός διανύσματος Α σε κάποιο άξονα με τον οποίο σχηματίζει γωνία 90-θ. Αν κάνετε ένα σχήμα στο τετράδιό σας, θα διακρίνετε το ορθογώνιο τρίγωνο που μας οδηγεί σε αυτό το συμπέρασμα.

Στη σύνθετη ταλάντωση στην οποία αναφερθήκαμε για την απομάκρυνση ισχύει x = A₁ημ(ωt+φ₁) + A₂ημ(ωt+φ₂).

Την αλγεβρική ποσότητα A₁ημ(ωt+φ₁) μπορούμε να τη «δούμε» και ως προβολή ενός διανύσματος Α₁ σε αντίστοιχο άξονα.

Αρκεί η γωνία που θα σχηματίζει με αυτόν να είναι 90- (ωt+φ₁).

Το ίδιο μπορούμε να πούμε και για την αλγεβρική ποσότητα A₂ημ(ωt+φ₂). Η τιμή της συμπίπτει με την προβολή ενός διανύσματος A₂

το οποίο σχηματίζει με το Α₁ γωνία φ₂-φ₁ .

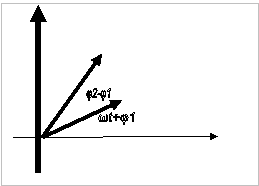Αν σχεδιάσουμε με τον νόμο του παραλληλογράμμου την ΣΥΝΙΣΤΑΜΕΝΗ Α των Α₁ και Α₂ θα ισχύουν τα εξής

1. η προβολή της στον άξονα θα είναι ίση με το άθροισμα των προβολών

των δύο διανυσμάτων A₁ημ(ωt+φ₁) + A₂ημ(ωt+φ₂).

(το αλγεβρικό άθροισμα των προβολών σε άξονα του επιπέδου είναι ίσο με την προβολή της συνισταμένης στον ίδιο άξονα )

2. η προβολή της στον άξονα θα έχει τιμή Αημ(ωt+φ₁ + θ)

Άρα

A₁ημ(ωt+φ₁) + A₂ημ(ωt+φ₂) = Αημ(ωt+φ₁+θ)

Το διάνυσμα λοιπόν που σχεδιάσαμε έχει μέτρο Α ίσο με το ΠΛΑΤΟΣ της σύνθετης ταλάντωσης και η γωνία που σχηματίζει με το διάνυσμα Α₁ είναι και η ΔΙΑΦΟΡΑ ΦΑΣΗΣ φάσης της σύνθετης ταλάντωσης από την ταλάντωση 1.

Μαθήτρια : - Κύριε . . . Δεν ξέρω αν κατάλαβαν οι συμμαθητές μου αλλά εγώ λίγα πράγματα κατάλαβα. Θα δοκιμάσω και μόνη μου .

Κατάλαβα όμως ότι η ΤΕΧΝΙΚΗ που μας προτείνετε δεν είναι αυθαίρετη .