Ανδρέας Ιωάννου Κασσέτας

Φυσική. ΑΣΕΠ 2009.

Τα θέματα και οι απαντήσεις

1. Μια σφαίρα μάζας m₁ συγκρούεται ελαστικά και κεντρικά με άλλη ακίνητη σφαίρα μάζας m₂.

Μετά την κρούση η σφαίρα με μάζα m₂ θα έχει μέγιστη κινητική ενέργεια αν ( αγνοώντας τη βαρύτητα ) ισχύει :

α. m₁ = m₂/4 β. m₁ = m₂/2 γ. m₁ = m₂ δ. m₁ = 2m₂

2. Ποια από τις παρακάτω σχέσεις ΔΕΝ μπορεί να περιγράψει το ηλεκτρικό πεδίο

Ε ( x,t) ενός αρμονικού ηλεκτρομαγνητικού κύματος το οποίο διαδίδεται στο κενό. Θεωρήστε

ως ταχύτητα του φωτός στο κενό c = 300.000km/s, x και t μετριούνται σε m και s αντίστοιχα και το Ε ( x,t) σε V/m.

α. E( x,t) = 10sin[ 2π(3.10⁸t – 10x) β. E( x,t) = 20sin[ 2π(6.10¹⁰t – 2.10²x)

γ. E( x,t) = 30sin[ 2π(9.10¹¹t – 3.10³x) δ. E( x,t) = 40sin[ 2π(10.10¹²t – 4.10⁴x)

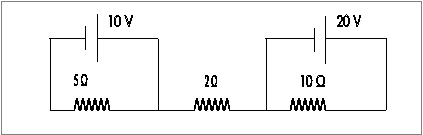
3. Στο κύκλωμα του σχήματος το ρεύμα που διαρρέει την αντίσταση R = 2 Ω θα έχει τιμή

α. 15 Α β. 5 Α γ. 2 Α δ. 0 Α

4. Το βάρος ενός αντικειμένου στην επιφάνεια της Σελήνης είναι το 1/5 του βάρους του στην επιφάνεια της Γης. Αν η περίοδος ταλάντωσης ενός απλού εκκρεμούς ( για μικρές γωνίες απόκλισης ) είναι 5 s, τότε η αντίστοιχη περίοδός του στην επιφάνεια της Σελήνης θα είναι : α. 1 s β. √5 s γ. 5√5 s δ. √5/5 s.

5. H θέση ως συνάρτηση του χρόνου t για μονοδιάστατη κίνηση ενός σωματιδίου δίνεται από τη σχέση x = 2t³ -6t² + 1200, όπου το x και το t μετριούνται σε m και s αντίστοιχα, Ποια είναι η μέση επιτάχυνση του σωματιδίου κατά τη διάρκεια του χρονικού διαστήματος

1 s ≤< t ≤ 3 s ;

α. 12 m/ s β. 16 m/ s γ. 18 m/ s δ. 20 m/ s

6. Ένα ηλεκτρόνιο ενέργειας Ε και ορμής p= ħk , όπου k >0 και ħ = h/2π, h = σταθερά του Planck) εισέρχεται από τα αριστερά στο σημείο x= 0 σε ένα δυναμικό ύψους V > E όπως φαίνεται στο σχήμα. Το χωρικό μέρος της κυματοσυνάρτησης του ηλεκτρονίου για x > 0

έχει τη μορφή α. e^-ax όπου α πραγματικός αριθμός β. e^-ikx γ. e^ikx δ. cos( kx)

7. Μια ιδανική πηγή τάσης V τροφοδοτεί το κύκλωμα που περιέχει τέσσερεις αντιστάσεις όπως στο σχήμα.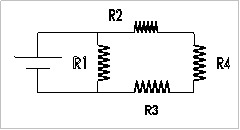

Αν η αντίσταση R₄ αυξηθεί ποια από τις παρακάτω προτάσεις είναι σωστή;

α. Το ρεύμα που διαρρέει την R₁ αυξάνεται

β. Η ισχύς που καταναλώνεται στην R₂ αυξάνεται

γ. Το ρεύμα που διαρρέει την R₂ μειώνεται

δ. Η τάση στα άκρα της R₁ αυξάνεται

8. Δύο σώματα μάζας m , 2m κινούνται σε κάθετες κατευθύνσεις με ταχύτητες υ , υ/2 αντίστοιχα και συγκρούονται πλαστικά.

Το μέτρο της ταχύτητας του συσσωματώματος που δημιουργείται από την πλαστική κρούση των σωμάτων θα είναι

α. 3υ/2 β. 2υ/3 γ. √2υ/3 δ. √3υ/2 .

9. Ένα αντιπρωτόνιο, ένα ποζιτρόνιο, ένα δευτέριο και ένα νετρόνιο κινούνται με την ίδια κινητική ενέργεια. Θεωρήστε ότι οι ταχύτητές τους είναι πολύ μικρότερες από την ταχύτητα του φωτός. Το μικρότερο μήκος κύματος de Broglie αντιστοιχεί στο :

α. ποζιτρόνιο β. αντιπρωτόνιο γ. νετρόνιο δ . δευτέριο

10. Ένας ομογενής οριζόντιος δίσκος Α περιστρέφεται με γωνιακή ταχύτητα ω γύρω από τον άξονά του που περνάει από το κέντρο μάζας του. Δύο δίσκοι Β και Γ πανομοιότυποι με τον Α αρχικά σε ηρεμία αφήνονται να πέσουν πάνω στον περιστρεφόμενο δίσκο Α. Η τελική γωνιακή ταχύτητα με την οποία θα περιστρέφεται το σύστημα των τριών δίσκων θα είναι :

α. ω β. ω/2 γ. ω/3 δ. 3ω/2

11. Θεωρήστε ένα μίγμα δύο μονοατομικών αερίων Α και Β, τα οποία βρίσκονται σε θερμική ισορροπία. Η μέση κινητική ενέργεια ενός μορίου του αερίου Α είναι Ε_k ( μετρούμενη σε joule ). Γνωρίζουμε ότι η μάζα του ατόμου του αερίου Β είναι τετραπλάσια από τη μάζα του ατόμου του αερίου Α. Η μέση κινητική ενέργεια μεταφοράς ενός μορίου του αερίου Β είναι :

α. Ε_k /4 β. Ε_k /2 γ. Ε_k δ 4Ε_k

12. Ένα αεροπλάνο πετάει με σταθερή οριζόντια ταχύτητα σε ύψος 1000 m πάνω από την επιφάνεια της Γης και δέχεται δυναμική άνωση Α₁. Το ίδιο αεροπλάνο πετάει με την ίδια οριζόντια ταχύτητα σε ύψος 2000 m και δέχεται δυναμική άνωση Α₂. Θεωρώντας ότι η επιτάχυνση της βαρύτητας έχει το ίδιο μέτρο στα δύο ύψη ισχύει ότι :

α. Α₂ = Α₁/4 β. Α₂ = Α₁/2 γ. Α₂ = 2Α₁ δ. Α₂ = Α₁

13. Δύο ομόκεντροι κυκλικοί αγωγοί ακτίνων a, b, διαρρέονται από ρεύμα Ι όπως φαίνεται στο σχήμα.

Ποιο είναι το μέτρο του μαγνητικού πεδίου στο σημείο Ο

( κοινό κέντρο των δύο ομόκεντρων κυκλικών αγωγών )

αν α= R και b = 2R ; ( μ₀ είναι η μαγνητική διαπερατότητα του κενού )

α. 3μ₀Ι/4R

β. μ₀Ι/4R

γ. 2μ₀Ι/3R

δ. μ₀Ι/3R

14. Το ακτινικό μέρος της κυματοσυνάρτησης de Broglie για ένα ηλεκτρόνιο στη βασική κατάσταση του ατόμου του υδρογόνου είναι

Ψ_1s ( r ) = A e ^–r/a0 όπου α₀ η ακτίνα του Bohr και Α είναι μια σταθερά που προσδιορίζεται από την κανονικοποίηση της κυματοσυνάρτησης. Η πιθανότητα να βρεθεί ένα ηλεκτρόνιο σε απόσταση r είναι ανάλογη της ποσότητας:

α. ∫e ^–2r/a0 r²dr β. ∫e ^–r/a0 r²dr γ. ∫e ^–2r/a0 dr δ. ∫e ^–r/a0 dr

15. Η μέση τιμή του τετραγώνου της ορμής p² ενός μονοδιάστατου αρμονικού ταλαντωτή μάζας και κυκλικής συχνότητας ω, ο οποίος βρίσκεται στη n-στάθμη είναι :

α. 0 β. ħmω(n + ½ ) γ . ħω (n + ½ ) δ. ħ/mω. (n + ½ )

16. Ποιο από τα παρακάτω φαινόμενα ερμηνεύτηκε με χρήση της σωματιδιακής φύσης του φωτός;

α. Πόλωση β. Φωτοηλεκτρικό φαινόμενο γ. Διάθλαση δ. Συμβολή

17. Ένας χώρος όγκου V γεμίζεται με ένα ιδανικό αέριο μάζας m σε απόλυτη θερμοκρασία Τ και πίεση Ρ. Κάποια στιγμή προσθέτουμε μια επιπλέον ποσότητα μάζας 3m του ίδιου ιδανικού αερίου και ο όγκος μειώνεται σε V/4 και η θερμοκρασία μειώνεται σε Τ/4. Η νέα πίεση του αερίου θα είναι: α. Ρ β. Ρ/4 γ. 4Ρ δ. Ρ/3

18. Όταν βομβαρδίσουμε έναν πυρήνα λιθίου ( ₃ ⁷Li ) με ένα άγνωστο σωματίδιο παρατηρούμε ότι παράγονται

δύο σωματίδια άλφα ( ₂ ⁴Ηe ) . Το άγνωστο σωματίδιο θα είναι :

α. φωτόνιο β. πρωτόνιο γ. νετρόνιο δ. δευτέριο

19. Σύμφωνα με την αρχή της αβεβαιότητας ή απροσδιοριστίας του Heisenberg, είναι αδύνατο να μετρηθούν ταυτόχρονα : α. η θέση και ο χρόνος β. η ορμή και η ενέργεια γ. η θέση και η ορμή δ. το φορτίο και η ενέργεια

20. Στο σχήμα φαίνεται η επαγόμενη ΗΕΔ Ε, που αναπτύσσεται ως συνάρτηση του χρόνου t σε ένα πλαίσιο το οποίο κινείται μέσα σε μαγνητικό πεδίο. Η απόλυτη τιμή της μεταβολής της μαγνητικής ροής |ΔΦ|, που διέρχεται μέσα από το πλαίσιο στο χρονικό διάστημα 0 ≤< t ≤ α, θα είναι :

( όπου Α θετική σταθερά )

α. |ΔΦ| = Α/α

β. |ΔΦ| = 0

γ. |ΔΦ| = Αα

δ. |ΔΦ|= ½Αα

21. Ένα ηλεκτρόνιο εισέρχεται με ταχύτητα υ σε κάποιο χώρο όπου υπάρχει ένα ομογενές ηλεκτρικό πεδίο . Για να μηδενιστεί κάποια στιγμή η ταχύτητά του, θα πρέπει (αγνοώντας τη βαρύτητα ) η ταχύτητα υ :

α. να είναι ομόρροπη με τις δυναμικές γραμμές του ηλεκτρικού πεδίου .

β. να είναι αντίρροπη με τις δυναμικές γραμμές του ηλεκτρικού πεδίου .

γ. να είναι κάθετη στις δυναμικές γραμμές του ηλεκτρικού πεδίου .

δ. να σχηματίζει γωνία 45⁰ τις δυναμικές γραμμές του ηλεκτρικού πεδίου .

22. θεωρήστε τρία ίσα θετικά φορτία τα οποία βρίσκονται στις κορυφές ενός ισόπλευρου τριγώνου με πλευρά α . Αν είναι U η δυναμική ενέργεια του ενός φορτίου που οφείλεται στις ηλεκτροστατικές δυνάμεις των άλλων δύο φορτίων, τότε ( αγνοώντας τη βαρύτητα ) η ολική δυναμική ενέργεια του συστήματος των τριών φορτίων θα είναι:

α. U/3 β. U γ. 3U/2 δ. 3U

23. Η μεταβολή από το σημείο Χ στο σημείο Υ ενός ιδανικού αερίου περιγράφεται στο σχήμα, όπου παρουσιάζεται το διάγραμμα πίεσης Ρ 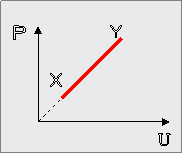ως συνάρτηση της εσωτερικής ενέργειας U ( η προέκταση του ευθύγραμμου τμήματος XY περνάει από την αρχή των αξόνων) .

Η μεταβολή αυτή είναι :

α. αδιαβατική

β. ισόχωρη

γ. ισοβαρής

δ. ισόθερμη

24. Για μονοχρωματικές ακτίνες φωτός ( κύματα φωτός ) που διέρχονται από τον αέρα σε ένα κομμάτι γυαλί ποια από τις παρακάτω προτάσεις είναι σωστή :

α. Η συχνότητα και το μήκος κύματος μειώνονται

β. Η συχνότητα αυξάνεται αλλά το μήκος κύματος μειώνεται

γ. Η συχνότητα παραμένει ίδια αλλά το μήκος κύματος μειώνεται

δ. Η συχνότητα και το μήκος κύματος παραμένουν αμετάβλητα

25. Στο κύκλωμα RLC του σχήματος, για ποια τιμή της αυτεπαγωγής L ( σε henries, H ) του πηνίου θα 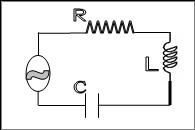πετύχουμε το φαινόμενο του συντονισμού ( μέγιστο πλάτος ρεύματος) με συχνότητα f = 100 Hz ;

Θεωρήστε R = 100 Ω και C = 100 μF.

α. 1 Η

β. 1/4π² Η

γ. 4π² Η

δ. 1/2π Η

26. Δύο μικρές φορτισμένες σφαίρες με μάζες m₁ και m₂ και φορτία q₁ > 0 και q₂ > 0 κρέμονται με δύο αβαρή νήματα ίσου μήκους L 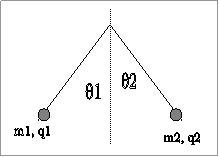όπως φαίνεται στο σχήμα. Αν θ₁ και θ₂ είναι οι αντίστοιχες γωνίες που σχηματίζουν οι σφαίρες

( θέλει να πει «τα δύο νήματα») με την κατακόρυφο όταν ισορροπούν και m₁ < m₂ τότε ποιο από τα παρακάτω ισχύει ; ( η επιτάχυνση της βαρύτητας είναι g )

a. θ₁ = θ₂ ≠ 0

β. θ₁ < θ₂

γ. θ₁ > θ₂

δ. θ₁ = 0 , θ₂= 0

27. Μια φορτισμένη σφαίρα ακτίνας R φέρει μια ακτινική πυκνότητα φορτίου η οποία είναι

ρ( r) = ar , a > 0 . Το μέτρο του ηλεκτρικού πεδίου στο εσωτερικό της σφαίρας σε απόσταση r = R/2 θα είναι:

( ε₀ η επιτρεπτότητα ή διηλεκτρική σταθερά του κενού). .

α. aR²/16ε₀ β. aR²/2ε₀ γ. aR/2ε₀ δ. a/ε₀

28. Ένα σωματίδιο μάζας m κινείται σε μία διάσταση με ταχύτητα η οποία δίνεται από τη σχέση υ(x) = ae^-bx , a > 0, b > 0 σταθερές και x η θέση του σωματιδίου. Η δύναμη που ασκείται στο σωματίδιο, ως συνάρτηση της θέσης, θα είναι :

α. –ma²be^-2bx β. –ma²be^-bx γ. - mabe^-bx δ . - mab²e^-2bx

29. Η ταχύτητα ενός σχετικιστικού σωματιδίου με ορμή 2 ΜeV/c και ολική ενέργεια 4 ΜeV θα είναι ( c η ταχύτητα του φωτός) α. c β. c/2 γ. c/4 δ. 3c/2

30. Ένα μεταλλικό τετραγωνικό πλαίσιο βρίσκεται εν μέρει μέσα σε ένα ομογενές μαγνητικό πεδίο Β ( 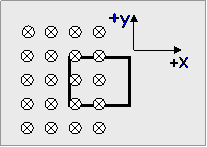κάθετο στη σελίδα με κατεύθυνση προς τη σελίδα όπως τη βλέπει ο αναγνώστης ) και μπορεί να κινηθεί στο δισδιάστατο επίπεδο xy μόνο παράλληλα στον άξονα x ή y, όπως φαίνεται στο σχήμα. Το επίπεδο του πλαισίου είναι συνεχώς κάθετο στις μαγνητικές γραμμές του μαγνητικού πεδίου που εκτείνεται σε όλο το αριστερό ημιεπίπεδο. Το επαγόμενο ρεύμα Ι, στο πλαίσιο θα έχει τη φορά κίνησης των δεικτών του ρολογιού εφόσον αυτό κινηθεί ως προς την κατεύθυνση :

α. – x β. - y γ. + x δ. + y

31. Οι καλύτεροι επιβραδυντές νετρονίων ( υλικά τα οποία σταματούν τα νετρόνια κυρίως μέσω ελαστικών κρούσεων) είναι : α. πυρήνες υδρογόνου ¹₁ Η

β. πυρήνες δευτερίου ²₁ Η γ. πυρήνες οξυγόνου ¹⁶₈ O δ. πυρήνες άνθρακα ¹²₆C

32. Ένα σκαθάρι αρχικά βρίσκεται στην περιφέρεια ενός οριζόντιου περιστρεφόμενου

( χωρίς τριβές ) δίσκου γύρω από κατακόρυφο άξονα που διέρχεται από το κέντρο μάζας του δίσκου, Ο. Το σκαθάρι αρχίζει να πλησιάζει τον άξονα περιστροφής κατά μήκος μιας ακτίνας του δίσκου. Ποια από τις παρακάτω προτάσεις είναι σωστή:

α. Η στροφορμή του συστήματος καθώς και η κινητική του ενέργεια διατηρούνται σταθερές.

β. Η στροφορμή του συστήματος διατηρείται σταθερή, ενώ η κινητική του ενέργεια συνεχώς αυξάνει ( θέλει να πει « ΑΥΞΑΝΕΤΑΙ» ) .

γ . Η στροφορμή του συστήματος μειώνεται ενώ η κινητική του ενέργεια παραμένει σταθερή

δ. Η στροφορμή του συστήματος διατηρείται σταθερή ενώ η κινητική του ενέργεια συνεχώς μειώνεται,

33. Δύο αρμονικές ταλαντώσεις x(t) , y(t) περιγράφονται από τις σχέσεις x(t) = x₀ cos(ωt) και y(t)= y₀sin( ωt+π/10) όπου x₀ > 0 , y₀ > 0 σταθερές, t είναι ο χρόνος και ω η κυκλική συχνότητα των αρμονικών ταλαντώσεων. Η απόλυτη τιμή της διαφοράς φάσης τους |Δφ| θα είναι: α. π/2 β. 2π/5 γ. 3π/5 δ. π/10

34. Ένα φορτισμένο σωματίδιο μάζας m και φορτίου q εκτοξεύεται κατακόρυφα προς τα πάνω με αρχική 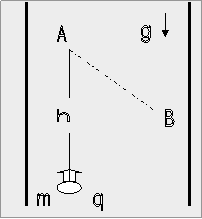ταχύτητα υ μέσα σε ένα αρχικά αφόρτιστο πυκνωτή όπου οι οπλισμοί απέχουν μια απόσταση d. Όταν το σωματίδιο φθάσει στο μέγιστο ύψος του h, εφαρμόζεται μια τάση V στους οπλισμούς του πυκνωτή, με αποτέλεσμα το σωματίδιο να ακολουθήσει την τροχιά ΑΒ η οποία σχηματίζει γωνία 45⁰ ως προς την κατακόρυφο,

όπως φαίνεται στο σχήμα.

Το φορτίο q του σωματιδίου θα είναι:

( επιτάχυνση βαρύτητας = g )

a. q = υ²/2g

β. q = V/d

γ. q = mgd/V

δ. q = mgd/Vυ

35. Σύμφωνα με το καθιερωμένο πρότυπο των στοιχειωδών σωματιδίων, ποιο από τα παρακάτω σωματίδια είναι στοιχειώδες;

α. Πρωτόνιο (p) β. Πιόνιο (π) γ. Νετρόνιο (n) δ. Μιόνιο (μ)

36. Μία δι(επαφή) δύο ημιαγωγών τύπου-n και τύπου-p επιτρέπει ευκολότερα τη δίοδο του ρεύματος όταν :

α. οι δύο ακροδέκτες Α και Β

φέρουν θετικά δυναμικά.

β. οι δύο ακροδέκτες Α και Β φέρουν αρνητικά δυναμικά

γ. ο ακροδέκτης Α φέρει θετικό δυναμικό ενώ ο ακροδέκτης Β φέρει αρνητικό δυναμικό

δ. ο ακροδέκτης Α φέρει αρνητικό δυναμικό ενώ ο ακροδέκτης Β φέρει θετικό δυναμικό

37. θεωρήστε μια διαχωριστική επιφάνεια υγρού – αέρα. Ο απόλυτος δείκτης διάθλασης του νερού είναι n_l = 2 n_a = 1 .

Η οριακή ( ορική ) γωνία θ_c για ολική ανάκλαση είναι:

α. 30⁰ β. 45⁰ γ. 60⁰ δ. 90⁰

38. Αναμειγνύουμε δύο ποσότητες ίδιων υγρών Α, Β, με συντελεστή ειδικής θερμότητας c. Έστω ότι η μάζα του υγρού Α είναι διπλάσια από τη μάζα του υγρού Β, δηλαδή m_A = 2 m_Β και η θερμοκρασία του υγρού Α είναι τριπλάσια από τη θερμοκρασία του υγρού Β,

δηλαδή Τ_Α = 3 Τ_Β. Όταν επέλθει η ισορροπία, η θερμοκρασία Τ του μείγματος θα είναι :

α. Τ= 4Τ_Β/3 β. Τ= 5Τ_Β/3 γ. Τ= 6Τ_Β/3 δ. Τ= 7Τ_Β/3

39. Το τεταρτημόριο ενός ομοιόμορφα φορτισμένου ( με αρνητικό φορτίο Q < 0 ) δακτυλίου ακτίνας R ασκεί μια δύναμη F σε ένα θετικό σημειακό φορτίο ( q< 0 ), το οποίο βρίσκεται στην αρχή των αξόνων όπως φαίνεται στο σχήμα. Το μέτρο της δύναμης F θα είναι:

( ε₀ είναι η επιτρεπτότητα ή διηλεκτρική σταθερά του κενού)

α. F = 1/4πε₀ . Qq/π R² β. F = 1/4πε₀. 2Qq/π R² .

γ. F = 1/4πε₀ . 2√2Qq/π R² . δ. F = 1/4πε₀ . Qq/ R² .

40. Μία συμπαγής σφαίρα ακτίνας R και μάζας M και ροπής αδράνειας Ι = 2ΜR²/5 ξεκινάει να κυλάει χωρίς ολίσθηση σε ένα κεκλιμένο επίπεδο από ύψος Η. Όταν φθάσει στο κατώτερο σημείο Β του κεκλιμένου επιπέδου έχει αποκτήσει ταχύτητα μέτρου υ_Μ .

Αν μια σημειακή μάζα m ακολουθήσει την ίδια διαδρομή χωρίς τριβή, τότε το μέτρο της ταχύτητάς της στο ίδιο σημείο θα είναι υ_m.

Ο λόγος των ταχυτήτων υ_Μ /υ_m θα είναι :

α. √2/2 β. √5/√7 γ. √2/√3 δ. 1

41. Η δυναμική ενέργεια ενός υλικού σημείου το οποίο κινείται στον τρισδιάστατο καρτεσιανό χώρο εξαρτάται από την απόσταση r και δίνεται από τη σχέση U ( r ) = A/rⁿ , όπου Α > 0 σταθερά και n ακέραιος θετικός αριθμός. Το διάνυσμα της δύναμης θα είναι : ( όπου r = r ř και ř το μοναδιαίο διάνυσμα στην κατεύθυνση του r) α. F = nA/rⁿ⁺².r β. F = nA/rⁿ⁺¹. r

γ. F = -nA/rⁿ⁺². r δ. F = - nA/rⁿ⁺¹. r

Τα σύμβολα F και r παριστάνουν διανύσματα

42. Θεωρήστε δύο όμοια παράλληλα φορτισμένα λεπτά φύλλα απείρων διαστάσεων τα οποία απέχουν μια απόσταση d.

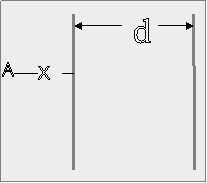Αν το φορτίο ανά μονάδα επιφάνειας σε κάθε επίπεδο είναι σ > 0,

τότε το μέτρο του ηλεκτρικού πεδίου στο σημείο Α θα είναι :

( ε₀ είναι η επιτρεπτότητα ή διηλεκτρική σταθερά του κενού)

α. 0

β. σ/ε₀

γ. σ/2ε₀

δ. 2σ/ε₀. x/(x+d)

43. Θεωρήστε ότι η μαγνητική ροπή ενός πρωτονίου είναι μ= 1,5.10^-26 J/T. Η απόλυτη τιμή της διαφοράς των δυναμικών ενεργειών αλληλεπίδρασης |ΔΦ| = |U₂ – U₁| του πρωτονίου με ένα μαγνητικό πεδίο Β = 2Τ όταν το σπιν του πρωτονίου είναι ομόρροπο

( U₁) και αντίρροπο ( U₂) με το μαγνητικό πεδίο θα είναι:

α. 0 J β. 1,5.10^-26 J γ. 3.10^-26 J δ 6.10^-26 J

44. Ακτίνες μονοχρωματικού ηλεκτρομαγνητικού κύματος φωτός πέφτουν σε μια διαχωριστική επιφάνεια δύο οπτικών μέσων με δείκτες διάθλασης n₁ και n₂ και ταχύτητες διάδοσης υ₁ και υ₂, όπως στο σχήμα. Η διαθλώμενη ακτίνα σχηματίζει γωνία θ_δ > θ_π με τον κατακόρυφο άξονα όπου θ_π είναι η γωνία που σχηματίζει η προσπίπτουσα ακτίνα με τον 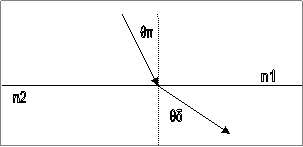κατακόρυφο άξονα.

Ποια από τις παρακάτω προτάσεις ΔΕΝ είναι σωστή ;

α. n₁ > n₂

β. υ₁ < υ₂

γ. Η συχνότητα των ηλεκτρομαγνητικών κυμάτων

δεν αλλάζει όταν αυτά διαδίδονται στα δύο μέσα

δ. Η προσπίπτουσα ακτίνα δεν μπορεί να υποστεί ολική ανάκλαση.

45. Αν η ακτίνα της Γης ( με επιτάχυνση βαρύτητας g στην επιφάνεια της Γης διπλασιαστεί, ενώ η μάζα της παραμείνει η ίδια, τότε η νέα επιτάχυνση της βαρύτητας στην επιφάνεια της Γης, g’, θα είναι:

α. g’ = 4g β. g’ = 2g γ. g’ = g/4 δ. g’ = g/2

46. Τρία όμοια σημειακά θετικά φορτία Α, Β, και Γ, με φορτίο q το καθένα, βρίσκονται στις κορυφές ενός τετραγώνου πλευράς L.

Το μέτρο της ηλεκτροστατικής δύναμης που ασκείται στο φορτίο ( αγνοώντας τη βαρύτητα ) θα είναι :

( ε₀ είναι η επιτρεπτότητα ή διηλεκτρική σταθερά του κενού)

α. 1/4πε₀ . q²/L²

β. √2/4πε₀. q²/L²

γ. 2/4πε₀. q²/L²

δ. 2√2/4πε₀. q²/L²

47. Ποια από τις παρακάτω συναρτήσεις μπορεί να περιγράψει ένα ηλεκτροστατικό πεδίο ( k > 0, x, y, z είναι τα μοναδιαία διανύσματα στις καρτεσιανές συντεταγμένες x, y , z )

α. E = k ( -y x + x y + z z) β. E = k ( y x - x y + z z)

γ. E = k (x x + y y + z z) δ. E = k (z x + z y - y z)

48. Ένας πυκνωτής ο οποίος αποτελείται από 2 επίπεδους οπλισμούς, που ο καθένας τους έχει εμβαδό Α και απέχουν μεταξύ τους μια απόσταση d, φορτίζεται με εφαρμογή μιας διαφοράς δυναμικού V μεταξύ των οπλισμών του. Αποσυνδέουμε τον πυκνωτή από την πηγή φόρτισής του και φέρνουμε τους δύο παράλληλους οπλισμούς σε απόσταση d/2 . Η νέα διαφορά δυναμικού μεταξύ των οπλισμών του πυκνωτή θα είναι :

α. 4V β. 2V γ.V/4 δ. V/2

49. Οι διάφοροι τύποι ηλεκτρομαγνητικής ακτινοβολίας είναι : 1. Ακτίνες Χ

2. Ραδιοκύματα 3. Ορατή ακτινοβολία 4. Υπέρυθρο 5. Υπεριώδες

Η σωστή κατάταξη των διάφορων τύπων ακτινοβολίας από το μικρότερο στο μεγαλύτερο

μήκος κύματος θα είναι : α. 1, 2, 3, 4, 5 β. 2, 3, 4, 5, 1

γ. 1, 5, 3, 4, 2 δ. 3, 4, 2, 1, 5

50. Δύο ομογενή μαγνητικά και ηλεκτρικά πεδία Ε και Β καταλαμβάνουν τον ίδιο χώρο. Εάν οι πυκνότητες ενέργειας του μαγνητικού και του ηλεκτρικού πεδίου είναι ίσες, τότε ο λόγος των μέτρων των πεδίων |Ε|/|Β| θα είναι: ( ε₀ , μ₀ είναι η επιτρεπτότητα ή διηλεκτρική σταθερά και η μαγνητική διαπερατότητα του κενού αντίστοιχα )

α. 1/ √(ε₀μ₀) β. √(ε₀μ₀) γ. √(ε₀/ μ₀) α. √(μ₀/ε₀)

51. Ένα φορτισμένο σωματίδιο φορτίου q εισέρχεται με αρχική ταχύτητα υ₀ = υ₀ x υ₀ > 0 σε μια περιοχή ομογενούς ηλεκτρικού και μαγνητικού πεδίου. Το μαγνητικό πεδίο είναι της μορφής Β = - Β₀ y , Β₀ > 0 . Αν θέλουμε το σωματίδιο να περάσει μέσα από την περιοχή των δύο πεδίων χωρίς απόκλιση, τότε το ηλεκτρικό πεδίο Ε πρέπει να έχει τη μορφή :

α. Ε =-υ₀Β₀ z β. Ε =υ₀Β₀ z γ. Ε =υ₀ /Β₀ z δ. Ε =υ₀Β₀ y

52. Ποια από τις παρακάτω διασπάσεις του στοιχειώδους σωματιδίου μιονίου μ^- είναι δυνατή ;

α. μ^- διασπάται σε e⁺ + ν_e β. μ^- διασπάται σε e^- + ν_e

γ. μ^- διασπάται σε e^- + ν_μ δ._. μ^- διασπάται σε e^- + ν_e + ν_μ

53. Θεωρήστε δύο φωτόνια Α, Β, τα οποία διαδίδονται στο κενό, με μήκος κύματος λ_Α = λ ,

λ_Β = 3λ. Ο λόγος των αντίστοιχων ενεργειών Ε_Α/ Ε_Β θα είναι :

α. 3 β. 1/3 γ. 9 δ. 1/9

54. Σωματίδιο μάζας m κινείται με ταχύτητα υ όπως φαίνεται στο σχήμα.

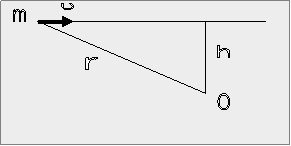Αν υ = | υ| και r = |r|,

το μέτρο της στροφορμής L = |L|,

του σωματιδίου ως προς το σημείο Ο είναι :

α. L = 0

β. L = mυh

γ. L = mυr

δ. L = mυr² .

55. Η ισοδύναμη χωρητικότητα του κυκλώματος μεταξύ των σημείων Α και Β, όπως

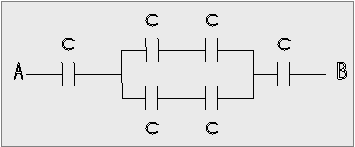φαίνεται στο σχήμα,

θα είναι:

α. C/2

β. C/3

γ. 3C

δ. 6C

56. Όταν αυξηθεί η τάση που εφαρμόζεται σε ένα καθοδικό σωλήνα παραγωγής ακτίνων Χ, τότε οι παραγόμενες ακτίνες στο εσωτερικό του καθοδικού σωλήνα , που βρίσκεται στο κενό, θα εμφανίζονται με : α. μεγαλύτερη ενέργεια β. μεγαλύτερη ταχύτητα

γ. μεγαλύτερο μήκος κύματος δ. μικρότερη ταχύτητα