Ανδρέας Ιωάννου Κασσέτας

1. Ο άνθρωπος/ερευνητής παρατηρώντας «αυτό που συμβαίνει» - το οποίο αποκαλεί ΦΑΙΝΟΜΕΝΟ- επιδιώκει

α. να το ΠΕΡΙΓΡΑΨΕΙ σε μια δική του γλώσσα και

β. να το ΕΡΜΗΝΕΥΣΕΙ έτσι ώστε να μπορεί ακόμα και να το ΠΡΟΒΛΕΠΕΙ.

Για να τα βγάλει πέρα με τους δύο αυτούς στόχους - περιγραφή και ερμηνεία - βασίζεται σε ΕΝΝΟΙΕΣ τις οποίες έχει ήδη οικοδομήσει – με διεργασίες αφαίρεσης - αλλά και σε καινούριες έννοιες τις οποίες επινοεί.

ΤΟ ΦΩΣ ΔΙΑΔΙΔΕΤΑΙ ΕΥΘΥΓΡΑΜΜΑ. ΜΙΑ ΘΕΩΡΙΑ

Ξεκινώντας από την παρατήρηση του ΦΑΙΝΟΜΕΝΟΥ « ΣΚΙΑ» , τόσο στα επίγεια («ευλογημένη» σκιά της καρυδιάς ) όσο και στα ουράνια ( έκλειψη Σελήνης ) , αλλά και σίγουρα επηρεασμένοι από τη γεωμετρική παράδοση των Αλεξανδρινών και από την γεωμετρική έννοια «ευθεία γραμμή» – οι άνθρωποι οδηγήθηκαν σε μια ΘΕΩΡΙΑ για ΕΥΘΥΓΡΑΜΜΗ ΔΙΑΔΟΣΗ του φωτός. Η ΘΕΩΡΙΑ υποδηλώνει ότι το φως ταξιδεύει μέσα από τον δρόμο με το μικρότερο μήκος, ο οποίος κατά τη διάδοση σε ομογενές μέσο είναι και ο δρόμος ο χρονικά πιο σύντομος.

Στα ταξίδια του δηλαδή σε ομογενές διαφανές μέσο το φως δεν χρειάζεται «να διαλέξει»

ανάμεσα στον δρόμο με το μικρότερο μήκος και στον δρόμο τον χρονικά πιο σύντομο. Οι δύο δρόμοι συμπίπτουν. Είναι η ΕΥΘΕΙΑ ΓΡΑΜΜΗ.

Η ΘΕΩΡΙΑ για ευθύγραμμη διάδοση μπορούσε να δώσει μια ερμηνεία στο φαινόμενο ΣΚΙΑ αλλά και στους νόμους του φαινόμενου ΑΝΑΚΛΑΣΗ.

Από όλους τους δρόμους που οδηγούν από το Α - μέσα από ανάκλαση στον καθρέφτη- στο Β 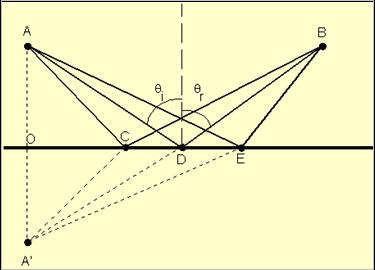ο ΑDB, είναι εκείνος με το πιο μικρό μήκος αλλά και ο χρονικά πιο σύντομος.

Μόνο μέσα από αυτόν τον δρόμο

«η γωνία πρόσπτωσης

είναι ίση με τη γωνία ανάκλασης».

Ο νόμος της ανάκλασης απορρέει

είτε από μια ΘΕΩΡΙΑ για ευθύγραμμη διάδοση ( τη διάδοση μέσα από το ελάχιστο ΜΗΚΟΣ διαδρομής ) είτε από μια ΘΕΩΡΙΑ για διάδοση μέσα από την χρονικά πιο σύντομη διαδρομή.

Τι θα κάνει, όμως, το φως εάν υποχρεωθεί να διαλέξει ανάμεσα στον δρόμο με το μικρότερο μήκος και σε εκείνον που είναι χρονικά πιο σύντομος ;

Τον πρώτο αιώνα μετά Χριστόν ο Ήρων ο Αλεξανδρινός ίσως ο πιο προικισμένος μηχανικός της εποχής του ενδιαφέρεται για τη διάδοση του φωτός σε συγκεκριμένο μέσο και προτείνει μια Αρχή σύμφωνα με την οποία για να ταξιδέψει το φως μέσα από ανακλάσεις σε καθρέφτες επιλέγει τον δρόμο με το μικρότερο μήκος.

Όταν όμως άρχισαν οι έρευνες για το φαινόμενο ΔΙΑΘΛΑΣΗ, ο οποιοδήποτε μπορούσε να διακρίνει ότι το φως δεν ακολουθεί τον δρόμο με το μικρότερο μήκος.

Χίλια περίπου χρόνια μετά τον Ήρωνα ο Άραβας Αλχάζεν διατυπώνει την υπόθεση ότι το φως, στα ταξίδια του, επιλέγει τον δρόμο τον χρονικά πιο σύντομο και υποστηρίζει ότι η υπόθεσή του θα μπορούσε να εξηγήσει τόσο το φαινόμενο ανάκλαση όσο και το φαινόμενο διάθλαση. Δεν θα μπορέσει βέβαια να τεκμηριώσει την υπόθεσή του διότι κανείς ακόμα δεν έχει ανακαλύψει το «μυστικό της διάθλασης» .

Έπρεπε να περάσουν εκατοντάδες χρόνια για να οδηγηθούν οι ερευνητές στην ανακάλυψη του μυστικού της διάθλασης.

Και αυτό το κατάφεραν οι Ολλανδοί σε μια εποχή που είναι πρωτοπόροι στην κατασκευή φακών και στις έρευνες για το φως .

Το 1621 ο Willebrord Snell «είδε» τη λύση του αινίγματος για τον νόμο της διάθλασης. Το φως «λοξοδρομεί» έτσι ώστε ο λόγος των ημιτόνων των γωνιών πρόσπτωσης και διάθλασης να είναι σταθερός. Η ανακάλυψη, νόμος του Snell, επανέφερε το ερώτημα « Μήπως η διάδοση του φωτός γίνεται μέσα από την πιο σύντομη χρονικά διαδρομή;»

Η ΑΡΧΗ ΤΟΥ ΦΕΡΜΑ. ΜΙΑ ΑΛΛΗ ΘΕΩΡΙΑ.

1657. Fermat. Η πρώτη απάντηση.

Τριάντα πέντε περίπου χρόνια μετά την ανακάλυψη του Snell και αφού εν τω μεταξύ στη Γαλλία

ο Descartes ( Καρτέσιος ) είχε επαναλάβει ( 1632 ) τις μετρήσεις με διάθλαση και είχε δημοσιεύσει τα συμπεράσματά του για τον νόμο ημπ/ημδ = σταθ . – στα γαλλικά σχολεία αναφέρεται ως Νόμος του Ντεκάρτ- ο επίσης Γάλλος Fermat ένας από τους μεγαλύτερους μαθηματικούς της εποχής, έσκυψε στο παλιό ερώτημα για τα μονοπάτια του φωτός και απέδειξε τεκμηριωμένα ότι

το φως σε όλα τα ταξίδια του ακολουθεί τη πορεία την χρονικά πιο σύντομη .

Αρχή του ελάχιστου χρόνου ή Αρχή του Fermat .

Le trajet parcouru par la lumière entre deux points est toujours celui qui minimise le temps de parcours

Πράγματι με αφετηρία την Αρχή αυτή και με όχι και τόσο δύσκολα μαθηματικά μπορεί να προκύψει ο νόμος της διάθλασης.

Μπορούμε με ποιητική άδεια να λέμε ότι το φως ΔΙΑΛΕΓΕΙ

Εξυπακούεται βέβαια ότι «το φως δεν σκέπτεται».

Εκείνος που σκέπτεται είναι ο άνθρωπος ο οποίος προκειμένου να ερμηνεύσει το φαινόμενο ΔΙΑΘΛΑΣΗ - το «γιατί το φως λοξοδρομεί με ορισμένο πάντα τρόπο» - ΟΔΗΓΕΊΤΑΙ ΣΤΟ ΝΑ ΔΙΑΤΥΠΩΣΕΙ ΜΙΑ ΘΕΩΡΙΑ,

την Αρχή του ελάχιστου χρόνου ή Αρχή του Fermat .

Βασιζόμενοι στην Αρχή του Fermat μπορούμε να αποδείξουμε ότι

Για να ταξιδέψει το φως από το σημείο Α σε 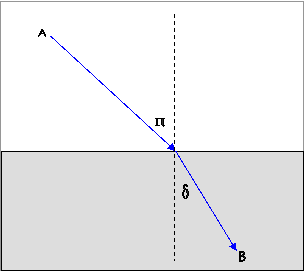σημείο Β - το οποίο βρίσκεται σε διαφορετικό διαφανές μέσο - ο χρονικά πιο σύντομος από όλους τους δρόμους είναι εκείνος για τον οποίο ο ΛΟΓΟΣ των ημιτόνων των γωνιών πρόσπτωσης και διάθλασης ( ημπ/ημδ) είναι ίσος με τον λόγο των ταχυτήτων του φωτός στα δύο μέσα .

Αυτό σημαίνει ότι το φως δεν ταξιδεύει από το Α στο Β μέσα από την ευθεία ΑΒ διότι το μήκος ΑΒ είναι η μικρότερη σε μήκος διαδρομή αλλά δεν είναι η πιο σύντομη.

Η Αρχή δηλαδή προσφέρει μια ερμηνεία τόσο στο γεγονός ότι το φως διαθλάται

όσο και στο γεγονός ότι διαθλάται σύμφωνα με τον νόμο «ημπ/ημδ = σταθερό».

2. Στο σχολικό βιβλίο της Γ΄ Γυμνασίου η Αρχή του ελάχιστου χρόνου παρουσιάζεται

(σελ. 123) κατά την περιγραφή της διάδοσης του φωτός σε ομογενές διαφανές μέσο. Ωστόσο

Κατά τη διάδοση του φωτός σε ομογενές μέσο « η Θεωρία για ευθύγραμμη διάδοση »

και « η Αρχή του ελάχιστου χρόνου ταυτίζονται ».

Η σε μήκος μικρότερη διαδρομή είναι και η χρονικά πιο σύντομη

Η συνέπεια είναι να μην μπορεί ένας μαθητής να διακρίνει έστω και ένα φυσικό φαινόμενο σχετιζόμενο με φως στο οποίο οι δύο έννοιες ΕΛΑΧΙΣΤΟ ΜΗΚΟΣ ΔΙΑΔΡΟΜΗΣ και ΕΛΑΧΙΣΤΟΣ ΧΡΟΝΟΣ «ΤΑΞΙΔΙΟΥ» να είναι διαφορετικές, μολονότι αυτό δηλώνεται με το παράδειγμα του οδηγού. Αυτό δημιουργεί ερωτήματα στον διδασκόμενο. «Τι μας χρειάζεται η Αρχή αυτή κατά τη διάδοση του φωτός σε ομογενές μέσο; »

« Κατά τη διάδοσή του σε ομογενές μέσο η διαδρομή με το μικρότερο μήκος και η διαδρομή η χρονικά πιο σύντομη συμπίπτουν. Γιατί η Αρχή επιμένει στη διαδρομή ελάχιστου χρόνου;»

« Εφόσον το φως ταξιδεύει όπως ένας βιαστικός που θέλει να πάει στη δουλειά του, το φως μπορεί και σκέπτεται;»

3. Θα μπορούσαν οι συγγραφείς - «να έχουν υπομονή» και - να παρουσιάσουν την Αρχή του Φερμά κατά τη διδασκαλία του φαινομένου ΔΙΑΘΛΑΣΗ. Μέσα από αυτό γίνεται κατανοητή η διάκριση των εννοιών ΕΛΑΧΙΣΤΟ ΜΗΚΟΣ ΔΙΑΔΡΟΜΗΣ και ΕΛΑΧΙΣΤΟΣ ΧΡΟΝΟΣ «ΤΑΞΙΔΙΟΥ» ακόμα και με το σχήμα της σελίδας 142.

4. Η διδακτική μας πρόταση είναι: Κατά τη περιγραφή της διάδοσης του φωτός σε ομογενές διαφανές μέσο Να αγνοείται από τον διδάσκοντα η Αρχή του Φερμά και να παρουσιάζεται κατά τη διδασκαλία του φαινομένου ΔΙΑΘΛΑΣΗ.

5. Huygens . H δεύτερη απάντηση το 1676.

Είκοσι πέντε περίπου χρόνια μετά τον Fermat ο Ολλανδός Christiaan Huygens θα υποστηρίξει ότι φως είναι ΚΥΜΑ και - χωρίς να χρησιμοποιήσει την Αρχή του ελάχιστου χρόνου - θα κάνει μια διαφορετική πρόταση για την ερμηνεία του πειραματικού νόμου της διάθλασης. Βασιζόμενος σε μια νέα Αρχή για τη διάδοση των κυμάτων - τη λεγόμενη Αρχή του Huygens - και στη Γεωμετρία απέδειξε γεωμετρικά ότι ακριβώς απέδειξε και ο Fermat , ότι ο λόγος ημπ/ημδ είναι ίσος με τον λόγο των ταχυτήτων του φωτός στα δύο μέσα. Βασιζόμενος στην ίδια Αρχή κατέληξε και στον νόμο της Ανάκλασης

6. Αξίζει να αναφέρουμε ότι

α. Η Αρχή του Fermat είναι δυνατόν να προκύψει από την Αρχή του Huygens

β. Η Αρχή του Fermat απορρέει από τη βασική Αρχή της Κβαντομηχανικής σύμφωνα με την οποία κάθε σωματίδιο ταξιδεύει μέσα από όλα τα πιθανά μονοπάτια και το άθροισμα όλων των πιθανών Κυματοσυναρτήσεων ( σε σημείο ανίχνεύσής του ) δίνει τη πιθανότητα να βρίσκεται το σωματίδιο στο σημείο αυτό.