Ανδρέας Ιωάννου Κασσέτας

Εκτός από ορισμένες αυτοδύναμες πηγές – όπως ο ήλιος, η 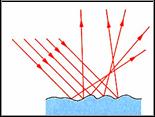πυγολαμπίδα, η φλόγα του κεριού και το πυρακτωμένο νήμα του ηλεκτρικού λαμπτήρα – τα περισσότερα αντικείμενα τα βλέπουμε επειδή αντανακλούν το φως που πέφτει πάνω τους.

Κάθε φορά που το φως πέφτει σε μια επιφάνεια ένα ποσοστό αντανακλάται οπωσδήποτε.

Η ανάκλαση του φωτός πάνω σε ειδικές κατοπτρικές επιφάνειες, έχει σαν συνέπεια να δημιουργούνται είδωλα σαν αυτά που βλέπουμε μέσα από καθρέφτες. Ο Νάρκισσος της ελληνικής μυθολογίας ερωτεύτηκε με πάθος το ίδιο το είδωλό του που έβλεπε να καθρεφτίζεται στο ακίνητο νερό .

Σε γλώσσα γεωμετρική

Τρεις περίπου αιώνες πριν από τον Χριστό ο Ευκλείδης παρουσίασε την περιγραφή της ανάκλασης σε «γλώσσα γεωμετρική» Σε δύο από τα έργα του – στο Οπτικά και στο Κατοπτρικά και παρουσιάζεται το μοντέλο της ΦΩΤΕΙΝΗΣ ΑΚΤΙΝΑΣ , το οποίο διατηρείται ως βασικό εργαλείο της Οπτικής μέχρι σήμερα. Για την περιγραφή του φαινομένου επιστρατεύονται οι γεωμετρικές έννοιες ΠΡΟΣΠΙΠΤΟΥΣΑ ΑΚΤΙΝΑ, ΑΝΑΚΛΩΜΕΝΗ ΑΚΤΙΝΑ, , ΕΠΙΦΑΝΕΙΑ ΠΡΟΣΠΤΩΣΗΣ , ΚΑΘΕΤΟΣ ΣΤΗΝ ΕΠΙΦΑΝΕΙΑ, ΕΠΙΠΕΔΟ ΠΡΟΣΠΤΩΣΗΣ, ΓΩΝΙΑ ΠΡΟΣΠΤΩΣΗΣ, ΑΝΑΚΛΩΜΕΝΗ ΑΚΤΙΝΑ, ΔΙΑΘΛΩΜΕΝΗ ΑΚΤΙΝΑ και ΓΩΝΙΑ ΑΝΑΚΛΑΣΗΣ .

Στο Κατοπτρικά διατυπώνεται και ένας νόμος για την ανάκλαση του φωτός, σύμφωνα με τον οποίο

«η γωνία πρόσπτωσης είναι ίση με τη γωνία ανάκλασης».

Τον 17^ο αιώνα ο Καρτέσιος διατυπωνει και έναν ακόμα 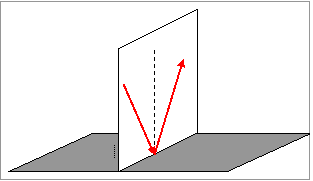νόμο.

Στο έργο του Διοπτρική - Dioptrique –

το 1637, αναφέρει ότι

«η ανακλώμενη ακτίνα

θα βρίσκεται πάντα στο επίπεδο

που ορίζουν η προσπίπτουσα ακτίνα

και η κάθετος στο σημείο πρόσπτωσης».

Κατοπτρική ανάκλαση και διάχυση

Η ανάκλαση σε καθρέφτη είναι μια ειδική περίπτωση ανάκλασης της οποία μπορούμε να χαρακτηρίσουμε κατοπτρική. Μια αποκλειστικά τέτοιου είδους ανάκλαση συμβαίνει εφόσον η ανακλαστική επιφάνεια είναι απολύτως λεία και στιλπνή. Όλες όμως οι επιφάνειες έχουν κάποιες ανωμαλίες και οι προσπίπτουσες ακτίνες 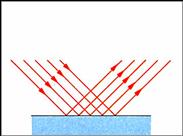ανακλώνται πάνω στις ανωμαλίες αυτές. Κάθε φωτεινή ακτίνα υπακούει στους νόμους της ανάκλασης, αλλά η ανακλώμενη δέσμη εμφανίζεται να διαχέεται προς όλες τις κατευθύνσεις με αποτέλεσμα να φθάνουν στα μάτια μας ανεξάρτητα από το «με ποια γωνία κοιτάζουμε την επιφάνεια» .

Η γενική αυτή περίπτωση ανάκλασης του φωτός αποτελεί το φαινόμενο ΔΙΑΧΥΣΗ χάρη στο οποίο βλέπουμε τα ετερόφωτα σώματα. Ακόμα και στην πιο λεία επιφάνεια ένα ποσοστό του φωτός θα ανακλαστεί με τη μορφή διάχυσης. Μπορούμε όμως να έχουμε μια ικανοποιητικά κατοπτρική ανάκλαση εφόσον οι ανωμαλίες της επιφάνειας έχουν μέγεθος της τάξης του μήκους κύματος του προσπίπτοντος φωτός.

Μια φωτεινή δέσμη είναι ένα σύνολο φωτεινών ακτίνων. Εφόσον οι ακτίνες ή οι γεωμετρικές του προεκτάσεις έχουν ένα κοινό σημείο, η δέσμη χαρακτηρίζεται στιγματική και το κοινό σημείο ΣΤΙΓΜΑ ( ή εστία ) της δέσμης.

Μια στιγματική δέσμη θα είναι ΑΠΟΚΛΙΝΟΥΣΑ

εφόσον οι ακτίνες προέρχονται από το στίγμα της

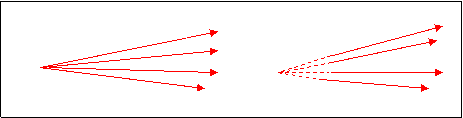
ή ΣΥΓΚΛΙΝΟΥΣΑ εφόσον οι ακτίνες

κατευθύνονται ( εστιάζουν ή επιδιώκουν να εστιάσουν ) σε αυτό.

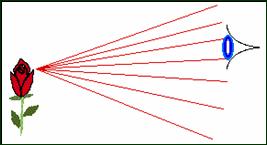
Όταν στο ανθρώπινο μάτι προσπέσει δέσμη αποκλίνουσα,

ο παρατηρητής εκλαμβάνει ως φωτεινό σημείο το στίγμα της.

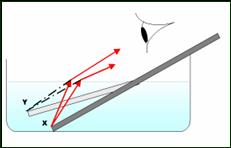
Η συγκλίνουσα δέσμη γίνεται αντιληπτή από τον άνθρωπο-παρατηρητή με τη βοήθεια πετάσματος ( οθόνης) τοποθετημένου στην εστία της. Το φως εστιάζει πάνω στο πέτασμα διαχέεται οπότε στον παρατηρητή δημιουργείται η αίσθηση ενός φωτεινού στίγματος στο πέτασμα.

Μια ειδική περίπτωση στιγματικής δέσμης η οποία δεν 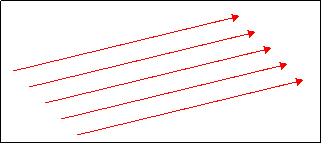καταχωρείται

ούτε στις συγκλίνουσες ούτε

στις αποκλίνουσες είναι

η κυλινδρική ( ή παράλληλη )

δέσμη φωτός της οποίας

η εστία θεωρείται στο άπειρο.

Οι φωτεινές δέσμες που δεν είναι στιγματικές χαρακτηρίζονται αστιγματικές.

1. Καθρέφτης επίπεδος

α. Είδωλο ενός φωτεινού σημειακού αντικειμένου.

Αν ένα φωτεινό σημειακό αντικείμενο Ο βρεθεί μπροστά σε επίπεδο κάτοπτρο, κάθε ακτίνα της αποκλίνουσας φωτεινής δέσμης που εκπέμπεται από αυτό ανακλάται σύμφωνα με τους νόμους της ανάκλασης, για να δημιουργηθεί μία επίσης αποκλίνουσα δέσμη η οποία εάν συναντήσει το μάτι μας θα βλέπουμε το στίγμα της «μέσα στον καθρέφτη».

Αυτό που βλέπουμε μέσα στον καθρέφτη είναι το ΦΑΝΤΑΣΤΙΚΟ ΕΙΔΩΛΟ από ανάκλαση του φωτεινού σημειακού αντικειμένου Ο .

Βασιζόμενοι στους νόμους της ανάκλασης και στην ευκλείδεια Γεωμετρία μπορούμε να αποδείξουμε ότι «σε σχέση με το Ο, το είδωλο Ι βρίσκεται σε θέση συμμετρική ως προς το επίπεδο της ανακλαστικής επιφάνειας» . Το αντικείμενο Ο και το είδωλο Ι ισαπέχουν από την επίπεδη κατοπτρική επιφάνεια.

β. Είδωλο ενός φωτεινού αντικειμένου με διαστάσεις.

Ένα φωτεινό αντικείμενο με διαστάσεις

θεωρούμε ότι αποτελείται από φωτεινά σημεία.

Αν το φωτεινό αντικείμενο βρεθεί

μπροστά σε επίπεδο κάτοπτρο,

κάθε φωτεινό σημείο του θα αποτελεί πηγή φωτεινών

ακτίνων και θα «δημιουργεί» ένα ΦΑΝΤΑΣΤΙΚΟ είδωλο

συμμετρικό ως προς το επίπεδο της κατοπτρικής επιφάνειας

Το φανταστικό αυτό είδωλο θα έχει

τις διαστάσεις

και τη μορφή

του φωτεινού

αντικειμένου .

2. Καθρέφτης κοίλος

Τα γεωμετρικά στοιχεία

α. Η επιφάνεια του κοίλου καθρέφτη. Είναι

τμήμα από την επιφάνεια μιας σφαίρας

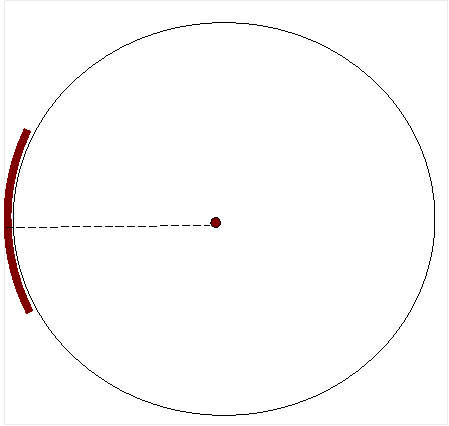β. Το κέντρο αυτής σφαίρας .

Λέγεται και «κέντρο του καθρέφτη»

γ. Η ακτίνα R της σφαίρας .

Λέγεται ακτίνα του καθρέφτη

δ. Η ευθεία που ενώνει το κέντρο

της σφαίρας και το μέσον του καθρέφτη.

Λέγεται ΚΥΡΙΟΣ ΑΞΟΝΑΣ

Τα ίδια γεωμετρικά στοιχεία

Χαρακτηρίζουν και έναν

καθρέφτη κυρτό

Το φως και ο κοίλος καθρέφτης.

Κάθε φωτεινή ακτίνα που πέφτει στον κοίλο καθρέφτη παράλληλη προς τον κύριο άξονα, μετά την ανάκλαση θα κατευθύνεται σε ένα σημείο Ε, την (κυρία) ΕΣΤΙΑ του καθρέφτη. Με βάση τους νόμους της διάθλασης και τη Γεωμετρία αποδεικνύεται ότι η ΕΣΤΙΑ βρίσκεται στο μέσο της απόστασης « κέντρο καθρέφτη – μέσο Ο του καθρέφτη» .

Η απόσταση δηλαδή της ΕΣΤΙΑΣ από τον καθρέφτη είναι ίση με το μισό της ακτίνας του καθρέφτη.

Η απόσταση αυτή λέγεται ΕΣΤΙΑΚΗ ΑΠΟΣΤΑΣΗ f. f = ½ R

Αυτό σημαίνει ότι αν πέσει στον καθρέφτη μια δέσμη φωτός παράλληλη προς τον κύριο άξονα θα «ΕΣΤΙΑΣΕΙ» στην εστία. Με μια τέτοια φωτεινή δέσμη και έναν κοίλο καθρέφτη θα μπορούσαμε εστιάζοντας το φως του ήλιου, να ανάψουμε φωτιά .

Το είδωλο στον κοίλο καθρέφτη

α. Πραγματικό είδωλο

Φανταζόμαστε ένα γραμμικό φωτεινό αντικείμενο ΑΒ κάθετο στον κύριο άξονα σε απόσταση μεγαλύτερη από την εστιακή. Σχηματίζουμε το είδωλο της κορυφής Α. Μια φωτεινή ακτίνα προερχόμενη από την κορυφή Α του αντικειμένου και παράλληλη προς τον κύριο άξονα, μετά την ανάκλαση στον καθρέφτη θα περάσει από την κύρια εστία . Μια άλλη φωτεινή ακτίνα προερχόμενη επίσης από την κορυφή Α η οποία προσπίπτει κάθετα στην επιφάνεια του καθρέφτη επιστρέφει από τον ίδιο δρόμο .

(Στην περίπτωση μιας σφαιρικής επιφάνειας ΚΑΘΕΤΟΣ στη σφαίρα είναι κάθε ευθεία που περνάει από το κέντρο ) . Στο σημείο Α΄ στο οποίο συναντώνται οι δύο ακτίνες θα είναι το σημείο στο οποίο θα συγκλίνουν όλες οι ακτίνες μετά την ανάκλαση, θα είναι το είδωλο του Α.

Θα μπορούσαμε επίσης να διαλέξουμε εκτός από τη φωτεινή ακτίνα την παράλληλη προς τον κύριο άξονα ως δεύτερη την ακτίνα η οποία διερχόμενη από την εστία, μετά την ανάκλαση θα γίνει παράλληλη προς τον κύριο άξονα. Το ζήτημα είναι ότι όλες οι προερχόμενες από το Α φωτεινές ακτίνες θα συγκλίνουν σε σημείο Α΄.

Αν φέρουμε την κάθετο από το Α΄ στον κύριο άξονα, το σημείο τομής με τον κύριο άξονα θα είναι το είδωλο Β΄ του φωτεινού σημείου Β . Το Α΄Β΄ είναι το « αντεστραμμένο» είδωλο του φωτεινού 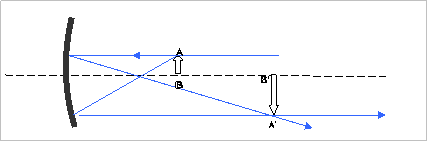αντικειμένου ΑΒ . Χαρακτηρίζεται είδωλο ΠΡΑΓΜΑΤΙΚΟ, διακρίνεται έτσι από τα φανταστικά είδωλα που βλέπουμε μέσα στους καθρέφτες .

Μπορούμε να το «δούμε» αν εκεί που δημιουργείται βάλουμε μια οθόνη.

Εάν για την απόσταση α του φωτεινού αντικειμένου από το κάτοπτρο ισχύει α > 2f το πραγματικό είδωλο θα είναι μικρότερο από το φωτεινό αντικείμενο. Εάν f < α < 2f το πραγματικό είδωλο θα είναι μεγαλύτερο από το φωτεινό αντικείμενο.

β. Φανταστικό είδωλο

Αν πλησιάσουμε το φωτεινό αντικείμενο «κοντά» στον κοίλο καθρέφτη θα δούμε

το είδωλο μέσα στον καθρέφτη. Θα είναι είδωλο ΦΑΝΤΑΣΤΙΚΟ.

Το «κοντά» σημαίνει σε απόσταση μικρότερη από την εστιακή.

Το φανταστικό είδωλο σε έναν κοίλο καθρέφτη θα είναι πάντα μεγαλύτερο από το φωτεινό αντικείμενο.

Για να δούμε δηλαδή τον εαυτό μας μέσα από τον κοίλο καθρέφτη πρέπει να πλησιάσουμε σε απόσταση μικρότερη από την εστιακή .

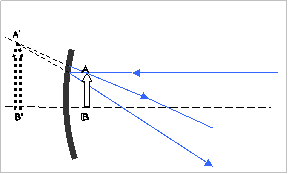
Για να σχεδιάσουμε το φανταστικό αυτό είδωλο του φωτεινού αντικειμένου ΑΒ, σχεδιάζουμε το είδωλο της κορυφής Α ( σχήμα ) . Από τις φωτεινές ακτίνες που προέρχονται από το Α διαλέγουμε δύο. Η μία είναι η παράλληλη προς τον κύριο άξονα η οποία μετά την ανάκλαση θα διέρχεται από την κυρία εστία. Η άλλη ακτίνα είναι η κάθετη στον καθρέφτη η οποία ανακλώμενη θα επιστρέψει από τον ίδιο δρόμο με αντίθετη κατεύθυνση. Διαπιστώνουμε ότι οι δύο ακτίνες δεν τέμνονται, αποκλίνουν. Τέμνονται όμως οι φανταστικές προεκτάσεις τους πίσω από τον καθρέφτη σε σημείο Α΄. Όλες οι ακτίνες οι προερχόμενες από το Α μετά την ανάκλαση συνιστούν αποκλίνουσα δέσμη με στίγμα πίσω από τον καθρέφτη σε σημείο Α΄. Το Α΄ είναι το φανταστικό είδωλο του Α. Φέρνουμε στην συνέχεια τη γεωμετρική κάθετο στον κύριο άξονα και εντοπίζουμε το σημείο Β, το φανταστικό είδωλο του Β.

3. Καθρέφτης κυρτός

Το φως και ο κυρτός καθρέφτης

Κάθε φωτεινή ακτίνα που πέφτει στον κυρτό 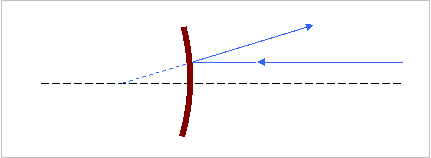καθρέφτη παράλληλη προς τον κύριο άξονα, μετά την ανάκλαση θα κατευθύνεται θα διαδίδεται έτσι ώστε η φανταστική της προέκταση να περνάει από την σε ένα σημείο Ε, την (κυρία) ΕΣΤΙΑ του κυρτού καθρέφτη η οποία βρίσκεται «πίσω» από τον καθρέφτη. Με βάση τους νόμους της διάθλασης και τη Γεωμετρία αποδεικνύεται ότι η ΕΣΤΙΑ βρίσκεται στο μέσο της απόστασης « κέντρο καθρέφτη – μέσο Ο του καθρέφτη» .

Η απόσταση αυτή λέγεται ΕΣΤΙΑΚΗ ΑΠΟΣΤΑΣΗ f. Αυτό σημαίνει ότι αν πέσει στον καθρέφτη μια δέσμη φωτός παράλληλη προς τον κύριο άξονα θα γίνει δέσμη αποκλίνουσα με στίγμα την κυρία εστία «πίσω» από τον καθρέφτη. Με έναν κυρτό καθρέφτη δεν θα μπορούσαμε εστιάζοντας το φως του ήλιου, να ανάψουμε φωτιά .

Το είδωλο στον κυρτό καθρέφτη.

Όπου και να βρίσκεται το φωτεινό αντικείμενο το είδωλο θα είναι ΦΑΝΤΑΣΤΙΚΟ και μικρότερο από το αντικείμενο.

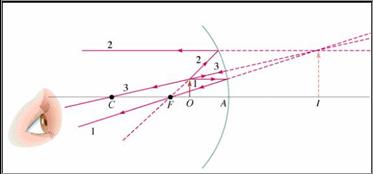
Φανταζόμαστε ένα γραμμικό φωτεινό αντικείμενο ΑΒ κάθετο στον κύριο άξονα. Σχηματίζουμε το είδωλο της κορυφής Α. Μια φωτεινή ακτίνα προερχόμενη από την κορυφή Α του αντικειμένου και παράλληλη προς τον κύριο άξονα, μετά την ανάκλαση στον καθρέφτη θα περάσει διαδίδεται έτσι 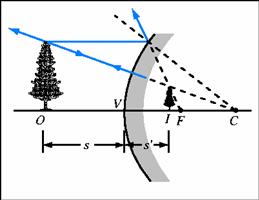ώστε η προέκτασή της «πίσω από τον καθρέφτη» να περνάει από την κύρια εστία . Μια άλλη φωτεινή ακτίνα προερχόμενη επίσης από την κορυφή Α η οποία προσπίπτει κάθετα στην επιφάνεια του καθρέφτη επιστρέφει από τον ίδιο δρόμο . Στο σημείο Α΄ «πίσω από τον καθρέφτη» στο οποίο συναντώνται οι προεκτάσεις των δύο ακτίνων θα είναι το σημείο στο οποίο θα προέρχονται όλες οι ακτίνες μετά την ανάκλαση, θα είναι το φανταστικό είδωλο του Α.

Αν φέρουμε την κάθετο από το Α΄ στον κύριο άξονα το σημείο τομής με τον κύριο άξονα θα είναι το είδωλο Β΄ του φωτεινού σημείου Β . Το Α΄Β΄είναι το « ορθό» ΦΑΝΤΑΣΤΙΚΟ είδωλο του φωτεινού αντικειμένου ΑΒ . Το βλέπουμε «μέσα στον καθρέφτη» .

καθρέφτης	ΦΑΝΤΑΣΤΙΚΟ είδωλο	ΠΡΑΓΜΑΤΙΚΟ είδωλο	Μέγεθος του φανταστικού ειδώλου
ΕΠΙΠΕΔΟΣ	σε κάθε περίπτωση	ποτέ	ίσο με το αντικείμενο
ΚΟΙΛΟΣ	εφόσον α < f	εφόσον α > f	μεγαλύτερο από το αντικείμενο
ΚΥΡΤΟΣ	σε κάθε περίπτωση	ποτέ	μικρότερο από το αντικείμενο

Οπτικό πεδίο; Τι είναι « οπτικό πεδίο» ;

Είναι μια περιοχή του χώρου μπροστά

από τον καθρέφτη στην οποία,

αν βρεθεί ένα αντικείμενο

θα το δεις μέσα στον καθρέφτη .

είναι μια μεγάλη περιοχή ;

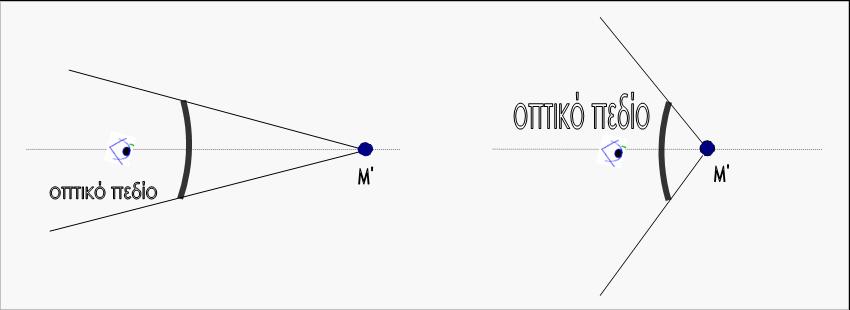
Εξαρτάται από το είδος και το μέγεθος του καθρέφτη και από τη θέση του παρατηρητή. Βρίσκεσαι λόγου χάρη μπροστά σε ένα ΕΠΙΠΕΔΟ κάτοπτρο. Φαντάσου το «είδωλο του ματιού σου» ως ένα γεωμετρικό σημείο Μ΄ ΣΥΜΜΕΤΡΙΚΟ ως προς τον καθρέφτη. Φέρε με τη φαντασία σου όλες τις ευθείες από το Μ΄ στην περιφέρεια του καθρέφτη και προέκτεινέ τις. Θα δημιουργηθεί ένας χώρος που θα είναι το ΟΠΤΙΚΟ ΠΕΔΙΟ.

Για κάθε φωτεινό αντικείμενο που θα βρεθεί σε αυτό τον χώρο, θα βλέπεις

το φανταστικό του είδωλο, θα μπορείς δηλαδή να το βλέπεις

μέσα στον καθρέφτη.

Υποθέτω ότι εάν μετακινηθεί ο παρατηρητής

το οπτικό πεδίο θα αλλάξει . . .

Ακριβώς

Τι γίνεται εάν το καθρέφτης είναι σφαιρικός ;

Με ανάλογο τρόπο θα φέρνεις στη σκέψη σου το φανταστικό είδωλο του ματιού σου. και μην ξεχνάς ότι τα είδωλα δεν είναι συμμετρικά . Στον κοίλο καθρέφτη το φανταστικό είδωλο δημιουργείται σε μεγαλύτερη απόσταση ενώ στον κυρτό σε μικρότερη. Γι αυτό και, υπό ίσους όρους, το οπτικό πεδίο του κυρτού καθρέφτη είναι ευρύτερο.

Α! Κατάλαβα . . γι αυτό στη Χώρα της Άνδρου,

εκεί στις στροφές για το Νηποριό,

βάζουν ΚΥΡΤΟΥΣ καθρέφτες.

Για να δημιουργείται μεγαλύτερο οπτικό πεδίο

Ακριβώς. Γι αυτό και στα αυτοκίνητο

ο καθρέφτης του οδηγού είναι ΚΥΡΤΟΣ

Οι ΚΟΙΛΟΙ καθρέφτες δίνουν μεγαλύτερα φανταστικά είδωλα αλλά το οπτικό τους πεδίο δεν είναι ευρύ

Οι ΚΥΡΤΟΙ καθρέφτες δίνουν μικρότερα φανταστικά είδωλα τα «φέρνουν κοντά» αλλά το οπτικό τους πεδίο είναι ευρύ