Τέσσερα προβλήματα

Τα τέσσερα προβλήματα συνιστούν πνευματική ιδιοκτησία

και . . παράκληση να μην χρησιμοποιηθούν από αντιγραφείς.

1. Η ομογενής τροχαλία στο σχήμα ισορροπεί με το νήμα πολλές φορές τυλιγμένο γύρω της. Η μία άκρη του νήματος

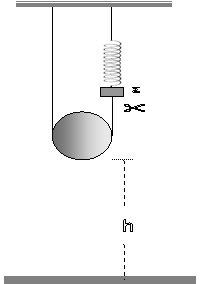είναι στερεωμένη στην οροφή και η άλλη στο σώμα Σ το οποίο ισορροπεί κρεμασμένο από κατακόρυφο ελατήριο. Η άνω άκρη του οποίου είναι επίσης στερεωμένη στο ταβάνι. Η μάζα της τροχαλίας είναι M =4 kg, η ακτίνα της R = 20 και η ροπή αδράνειας ως προς άξονα κάθετο στο επίπεδό της ο οποίος διέρχεται από το κέντρο μάζας της δίνεται από τη σχέση Ι= ½ΜR² . Η μάζα του σώματος Σ, το οποίο θεωρείται σημειακό αντικείμενο, είναι 2 kg. To νήμα και το ελατήριο έχουν αμελητέα μάζα. Το κατώτερο σημείο της τροχαλίας απέχει από το έδαφος κατά h

α. Να προσδιορίσετε τη δύναμη που ασκεί το ελατήριο στο σώμα Σ.

Σε κάποια χρονική στιγμή κόβουμε το νήμα στο σημείο σύνδεσης με το σώμα Σ και

το Σ, στο άκρο του ελατηρίου, εκτελεί αμείωτη αρμονική ταλάντωση. Διαπιστώνεται ότι τη στιγμή που για πρώτη φορά μηδενίζεται στιγμιαία η ταχύτητα του Σ, το κατώτερο σημείο της τροχαλίας φθάνει στο έδαφος.

Η αντίσταση του αέρα θεωρείται αμελητέα και η τιμή της βαρυτικής επιτάχυνσης

10 m/s² . Αν χρειαστεί να θεωρήσετε π² = 10.

Σας ζητούμε να υπολογίσετε β. το ύψος h.

γ. τη μέγιστη ταχύτητα του Σ κατά τη διάρκεια της ταλάντωσής του .

δ. τη στροφορμή της τροχαλίας ως προς το κέντρο της τη στιγμή που αγγίζει το έδαφος

2.Ένας χάρακας μάζας m = 100 g και μήκους L = 30 cm τοποθετείται κατακόρυφος στο χείλος του τραπεζιού, το οποίο απέχει h από οριζόντιο έδαφος. Αφήνουμε τον χάρακα ελεύθερο και αυτός στρεφόμενος γύρω από το κατώτερο άκρο του Ο εγκαταλείπει το τραπέζι τη στιγμή που γίνεται οριζόντιος . Διαπιστώνουμε ότι ο χάρακας φθάνει στο έδαφος τη στιγμή που για πρώτη φορά ξαναγίνεται οριζόντιος.

Να προσδιορίσετε α. την ταχύτητα του κέντρου μάζας του χάρακα τη στιγμή που εγκαταλείπει το τραπέζι β. το χρονικό διάστημα από τη στιγμή που εγκαταλείπει το τραπέζι μέχρι τη στιγμή που φθάνει στο έδαφος

γ. το ύψος h δ. την, ως προς το κέντρο μάζας, στροφορμή του χάρακα τη στιγμή που φθάνει στο έδαφος καθώς και τον ρυθμό μεταβολής της στροφορμής αυτής τη στιγμή εκείνη.

Η αντίσταση του αέρα θεωρείται αμελητέα και η τιμή της βαρυτικής επιτάχυνσης 10 m/s² .

Ο χάρακας έχει μορφή μονοδιάστατης ομογενούς ράβδου. Η ροπή αδράνειας ως προς άξονα κάθετο στη διεύθυνσή του, ο οποίος περνά από το κέντρο μάζας δίνεται από τη σχέση Ι_cm = 1/12 mL² . Η αντίσταση του αέρα θεωρείται αμελητέα και η τιμή της βαρυτικής επιτάχυνσης 10 m/s² .

3. Τα δύο σώματα Σ₁ και Σ₂ θεωρούνται σημειακά αντικείμενα και ισορροπούν δεμένα στο άκρο αβαρούς τεντωμένου νήματος. Το Σ₂ έχει μάζα 3 kg και ισορροπεί λόγω της στατικής τριβής από το δάπεδο ενώ το Σ₁ ισορροπεί πάνω στη σανίδα με την οποία δεν εμφανίζει τριβή. Η σανίδα έχει μήκος 4 m, μάζα 4 kg και είναι ομογενής δεν αγγίζει την τροχαλία και η τριβή με το κατακόρυφο τοίχωμα στο οποίο στηρίζεται είναι αμελητέα . Στην κατάσταση ισορροπίας που εμφανίζεται στο σχήμα, το Σ₁ απέχει από το κάτω άκρο Α της σανίδας 1 m και η σανίδα σχηματίζει γωνία 45^ο με το οριζόντιο έδαφος. Το Σ₁ έχει μάζα 1 kg και το Σ₂ ισορροπεί οριακά ευρισκόμενο σε κατάσταση επικείμενης ολίσθησης. Η ροπή αδράνειας της τροχαλίας θεωρείται αμελητέα και ο συντελεστής στατικής τριβής της σανίδας με το έδαφος είναι μ = 0,5.

Α. α . Να σημειώσετε τις δυνάμεις που ασκούνται στο Σ₁ και στη συνέχεια τις δυνάμεις που ασκούνται στο Σ₂ .

β. Να υπολογίσετε τον συντελεστή στατικής τριβής ανάμεσα στο Σ₂ και τη δάπεδο.

γ. Να προσδιορίσετε τις δυνάμεις που ασκούνται στη σανίδα

Β. Ασκούμε στο Σ₂ οριζόντια σταθερή δύναμη 15 Ν και το Σ₁ ανέρχεται στη σανίδα

α. Να προσδιορίσετε την επιτάχυνση του Σ₂ .

β. Σε ποια θέση θα βρίσκεται το Σ₁ τη στιγμή που η σανίδα παύει να ισορροπεί ; Πότε θα συμβεί αυτό ;

Η αντίσταση του αέρα θεωρείται αμελητέα και η τιμή της βαρυτικής επιτάχυνσης 10 m/s² . Να θεωρήσετε √2 = 1,4.

4. Στο σχήμα εμφανίζονται σε κάτοψη δύο σώματα Σ₁ και Σ₂ τα οποία ισορροπούν σε λείο οριζόντιο επίπεδο δεμένα στα άκρα ελατηρίων με σταθερές k₁ = 80 Ν/m 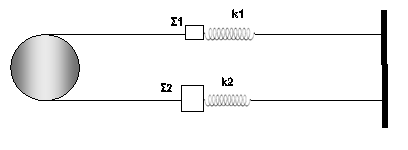και k₂ = 120 Ν/m τα οποία βρίσκονται στο φυσικό τους μήκος. Τα δύο σώματα συνδέονται με αβαρές νήμα μέσα από τροχαλία η οποία μπορεί να στρέφεται χωρίς τριβές γύρω από σταθερό κατακόρυφο άξονα διερχόμενο από το κέντρο της Ο. Η τροχαλία έχει μάζα M = 6 kg, ακτίνα R = 20 cm και ροπή αδράνειας ως προς τον κατακόρυφο άξονα τον διερχόμενο από το κέντρο της για την οποία ισχύει Ι₀ = ½ ΜR².

Σε μια χρονική στιγμή κάποιος παρεμβαίνει και μετακινεί το σώμα Σ₁ προς τα δεξιά συμπιέζοντας το ελατήριο k₁ κατά 10 cm και αφήνει το σύστημα να κινηθεί ελεύθερο. α . Να αποδείξετε ότι η επιτάχυνση του Σ₁ έχει σε κάθε χρονική στιγμή τιμή ανάλογη με την απομάκρυνση από τη θέση ισορροπίας . β. Να υπολογίσετε το χρονικό διάστημα μεταξύ δύο διαδοχικών μηδενισμών της γωνιακής ταχύτητας της τροχαλίας. γ. Να υπολογίσετε την τιμή της μέγιστης στροφορμής της τροχαλίας δ. Να υπολογίσετε τον ρυθμό μεταβολής της στροφορμής της τροχαλίας τη στιγμή που το ελατήριο έχει για πρώτη φορά συμπίεση ίση με 5 cm.

Να θεωρήσετε ότι το νήμα δεν ολισθαίνει ως προς την τροχαλία.

Κώστας Γεωργακόπουλος

Καθηγητής Δευτεροβάθμιας