Ένα πρόβλημα βαθμολόγησης

για το θέμα 4 στη Φυσική Κατεύθυνσης

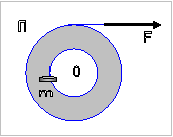
Στερεό Π μάζας Μ = 10 kg αποτελείται από δύο κολλημένους ομοαξονικούς κυλίνδρους με ακτίνες R και 2R όπου R= 0,2 m όπως στο σχήμα. Η ροπή αδράνειας του στερεού Π ως προς τον άξονα περιστροφής του είναι Ι = ΜR² . Το στερεό Π περιστρέφεται χωρίς τριβές γύρω από σταθερό οριζόντιο άξονα Ο΄Ο που συμπίπτει με τον άξονά του. Το σώμα Σ μάζας m = 20 kg κρέμεται από το ελεύθερο άκρο αβαρούς νήματος που είναι τυλιγμένο στον κύλινδρο ακτίνας R. Γύρω από το τμήμα του στερεού Π με ακτίνα 2R είναι τυλιγμένο πολλές φορές νήμα, στο ελεύθερο άκρο Α του οποίου μπορεί να ασκείται οριζόντια δύναμη F.

Τη χρονική στιγμή t₀ = 0 που το σύστημα του σχήματος είναι ακίνητο αυξάνουμε τη δύναμη ακαριαία έτσι ώστε να γίνει F = 115 N

β. Να βρείτε την επιτάχυνση του σώματος Σ .

Μια «λογική» λύση η οποία και προτείνεται είναι να εφαρμοστεί ο δεύτερος νευτωνικός νόμος της κίνησης στο κινούμενο ευθύγραμμα σώμα Σ και στη συνέχεια ο λεγόμενος θεμελιώδης νόμος για τη στροφική κίνηση στο στρεφόμενο σώμα Σ .

Ορισμένοι από τους εξεταζόμενους υπολόγισαν τη ζητούμενη τιμή της επιτάχυνσης με εφαρμογή του νόμου για τη στροφική κίνηση στο ΣΥΣΤΗΜΑ «στερεό Π, νήματα και σώμα Σ» .

Σημειώνουμε τις εξωτερικές δυνάμεις . Είναι η F, η βάρος mg του Σ, η βάρος του Π και δυνάμεις στήριξης ασκούμενες στον άξονα. Η ολική ροπή F.2R - mgR οπότε

F.2R - mgR = (ΜR² +mR²)α_γων

και α = α_γωνR οπότε και

α = (2F – mg)/(Μ+m) α = 1 m/s² .

Μπορούμε

να το θεωρήσουμε σωστό ;

Η άποψή μου είναι ότι η σχέση τ = (ΜR² +mR²)α_γων είναι σωστή και ότι υπάρχει τρόπος να αποδειχθεί η ορθότητά της με εφαρμογή του δεύτερου νόμου για τη στροφική κίνηση

στο ΣΥΣΤΗΜΑ «στερεό Π, νήματα και σώμα Σ» .

Βέβαια σημασία δεν έχει το ότι είναι σωστή αλλά το «πώς καταλήγει κανείς στην ορθότητά της» .

Το ταξίδι είναι εκείνο που έχει σημασία και όχι η Ιθάκη.

Δημιουργήθηκαν διαφωνίες μεταξύ συναδέλφων βαθμολογητών σε πολλά εξεταστικά κέντρα.

Γεννήθηκαν ερωτήματα βάσιμα τα οποία πρέπει να απαντηθούν.

1. Μπορεί το κινούμενο ευθύγραμμα υλικό σημείο να έχει γωνιακή επιτάχυνση ; μπορεί να έχει στροφορμή ;

2. Τι θα γίνει με τη ροπή αδράνειας του Σ η τιμή της οποίας είναι χρονικά μεταβαλλόμενη ;

3. Πώς θα εφαρμόσουμε τον νόμο για τη στροφική κίνηση σε ένα σύστημα ένα μέρος του οποίου εκτελεί στροφική κίνηση και ένα άλλο – υλικό σημείο μάζας m – κινείται ευθύγραμμα ;

Εκτιμούμε πάντως ότι οι διαφωνίες είναι δικαιολογημένες δεδομένου ότι :

α. Στη διατύπωση υπονοείται ότι το σώμα Σ είναι υλικό σημείο αλλά δεν αναφέρεται ρητά μόλο που είναι υλικό σημείο

β. Στο πρόγραμμα σπουδών και στο σχολικό βιβλίο οι έννοιες «στιγμιαία γωνιακή ταχύτητα υλικού σημείου», «στιγμιαία γωνιακή επιτάχυνση υλικού σημείου» και «στροφορμή υλικού σημείου» ορίζονται ανεπαρκώς και μόνο για κυκλική κίνηση.

γ. Πουθενά δεν δια φαίνεται ότι σε ένα σύστημα αναφοράς, οι τρεις αυτές έννοιες/διανυσματικά μεγέθη ορίζονται αναφορικά με ένα γεωμετρικό σημείο – αρχή των αξόνων Ο – και ανεξάρτητα από το είδος της κίνησης. Βέβαια αποκτούν ιδιαίτερη σημασία σε φαινόμενα όπως η «κυκλική κίνηση» και ακόμα μεγαλύτερο καθεμιά από αυτές ως γωνιακή ταχύτητα στρεφόμενου στερεού, γωνιακή επιτάχυνση στρεφόμενου στερεού και στροφορμή στρεφόμενου στερεού.

δ. Είναι αδύνατον διαβάζοντας κανείς το σχολικό βιβλίο να δώσει μια απάντηση στο «γιατί ο δεύτερος νόμος με τη μορφή τ = dL/dt αποτελεί τη γενικότερη διατύπωση του τ = Ια_γων ; ». Δεν υπάρχει ούτε ένα παράδειγμα που να δείχνει ότι σε αυτή την περίπτωση ισχύει ο γενικότερος και δεν ισχύει ο τ = Ια_γων .

Θα επιχειρήσουμε κάποιες απαντήσεις στα ερωτήματα

1. Μπορεί το κινούμενο ευθύγραμμα υλικό σημείο να έχει γωνιακή επιτάχυνση ;

Μπορεί να έχει στροφορμή;

Στο ερώτημα « μα πώς μπορεί - σε ένα ορισμένο σύστημα αναφοράς- ένα κινούμενο ευθύγραμμα υλικό σημείο να έχει στιγμιαία γωνιακή ταχύτητα ως προς Ο ;» η απάντηση βρίσκεται στον ορισμό της έννοιας «γωνιακή ταχύτητα».

Η γωνιακή ταχύτητα υλικού σημείου – όπως και η χρονική παράγωγός της γωνιακή επιτάχυνση - δεν ορίζονται για ορισμένο είδος κίνησης αλλά παρουσιάζουν ιδιαίτερο ενδιαφέρον όταν η κίνηση είναι κυκλική . Αν ένα υλικό σημείο έχει ταχύτητα ως προς κάποιο σύστημα αναφοράς έχει και γωνιακή ταχύτητα ως προς κάποιο Ο – αρχή των αξόνων. Αν το διάνυσμα θέσης σε κάποια χρονική στιγμή είναι r και η στιγμιαία ταχύτητα υ , η στιγμιαία γωνιακή ταχύτητα ορίζεται από το εξωτερικό γινόμενο

υ = ω x r , όπου τα υ, ω, r είναι διανύσματα.

Το ίδιο ισχύει και για τη «στιγμιαία στροφορμή υλικού σημείου ως προς Ο». Ορίζεται – σε κάποιο σύστημα αναφοράς - ως εξωτερικό γινόμενο «θέση x ορμή» ανεξάρτητα από το είδος της κίνησης του υλικού σημείου. Παρουσιάζει βέβαια ιδιαίτερο ενδιαφέρον ως στροφορμή υλικού σημείου σε κυκλική κίνηση και ως στροφορμή στρεφομένου στερεού.

Στο ερώτημα « σε τι μας χρειάζεται η γωνιακή ταχύτητα και η γωνιακή επιτάχυνση ενός υλικού σημείου κινουμένου ευθύγραμμα ;» η απάντηση είναι ότι σε πολύ λίγες περιπτώσεις μας χρειάζεται αλλά έστω και σε αυτές μας χρειάζεται .

Ένα παράδειγμα . Ένας κυλιόμενος δίσκος σε οριζόντιο έδαφος με το κέντρο μάζας να κινείται ευθύγραμμα και με επιτάχυνση . Η κίνηση του τροχού μπορεί να θεωρηθεί «στροφική περί ΣΤΙΓΜΙΑΙΟ άξονα διερχόμενο από το σημείο στήριξης Α». Σε αυτή τη θεώρηση το κέντρο μάζας έχει στιγμιαία γωνιακή ταχύτητα και στιγμιαία γωνιακή επιτάχυνση. Αυτό θα πει ότι ενώ το κέντρο μάζας κινείται ευθύγραμμα, υπό ορισμένη θεώρηση, έχει στιγμιαία γωνιακή επιτάχυνση ως προς κάποιο σημείο.

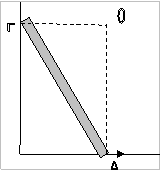
Ένα ακόμα παράδειγμα. Η ομογενής σκάλα ΓΔ αφήνεται και ολισθαίνει χωρίς τριβή όπως στο σχήμα.

Η κίνησή της μπορεί να θεωρηθεί στροφική περί στιγμιαίο άξονα Ο.

Το άκρο Δ, μολονότι κινείται ευθύγραμμα, έ

χει στιγμιαία γωνιακή ταχύτητα ως προς Ο.

Το ίδιο συμβαίνει και με το άκρο Γ.

Στην περίπτωση βέβαια του κινούμενου ευθύγραμμα υλικού σημείου Σ το οποίο έχει σε κάθε στιγμή μια γωνιακή ταχύτητα ω_Σ ως προς Ο αν θελήσουμε να συσχετίσουμε την ω_Σ με την ως προς Ο στιγμιαία γωνιακή ταχύτητα του τροχού ω θα έχουμε. Στροφορμή ως προς Ο = mυR = mx²ω_Σ - x η απόσταση του Σ από το Ο – άρα υR = x²ω και επειδή υ = ωR ωR² = ω_Σx² . ω_Σ = ωR² /x² .

2. Τι θα γίνει με τη ροπή αδράνειας του Σ η τιμή της οποίας είναι χρονικά μεταβαλλόμενη ;

3. Πώς θα εφαρμόσουμε τον νόμο για τη στροφική κίνηση σε ένα σύστημα ένα μέρος του οποίου εκτελεί στροφική κίνηση και ένα άλλο – υλικό σημείο μάζας m – κινείται ευθύγραμμα ;

Στο σημείο αυτό βρίσκεται και η απάντηση στο ερώτημα « από ποια άποψη ο δεύτερος νόμος με τη μορφή τ = dL/dt αποτελεί τη γενικότερη διατύπωση του τ = Ια_γων ;».

Ο νόμος με τη μορφή τ = dL/dt

α. αναφέρεται σε οποιοδήποτε σώμα ή σύστημα σωμάτων.

β. τ = dL/dt τ = d(Ιω)/dt τ = Ιdω/dt + ωdI/dt τ = Ια_γων + ωdI/dt είναι γενικότερος διότι καλύπτει και την περίπτωση με μεταβαλλόμενη ροπή αδράνειας. Μόνο αν η ροπή αδράνειας είναι σταθερή προκύπτει η τ = Ια_γων

Μια ΛΥΣΗ βασιζόμενη στον νόμο τ = dL/dt Το κινούμενο ευθύγραμμα υλικό σημείο Σ ΕΧΕΙ

( στιγμιαία ) ΣΤΡΟΦΟΡΜΗ ως προς Ο ίση με mυR ενώ το στερεό Π έχει στιγμιαία στροφορμή ως προς Ο ίση με Ιω.

Αν είναι L η στιγμιαία στροφορμή του συστήματος

L = mυR + Ιω .

Αν εφαρμόσουμε τον δεύτερο νόμο με τη γενικευμένη μορφή στο ΣΥΣΤΗΜΑ «στερεό Π, νήματα και σώμα Σ

τ = dL/dt. τ = mRdυ/dt + Idω/dt + ωdI/dt.

Εφόσον dI/dt = 0 dυ/dt = α και dω/dt = α_γων . τ = maR + Iα_γων . F.2R - mgR = (ΜR² +mR²)α_γων .

Το να εφαρμόσουμε τον δεύτερο νόμο του Νεύτωνα - με τη γενικότερη μορφή - στο ΣΥΣΤΗΜΑ «στερεό Π, νήματα και σώμα Σ» οδηγεί στην καλύτερη κατά την άποψή μου λύση.

Εξάλλου ο δεύτερος νόμος με τη γενικότερη διατύπωση δεν έχει τα μειονέκτημα του νόμου με τη μορφή τ = Ια_γων

Συμπέρασμα . Η σχέση τ = (ΜR² +mR²)α_γων είναι σωστή αλλά η απόδειξη για την ορθότητά της δεν μπορεί να γίνει με εφαρμογή της τ = Ια_γων . σε μια τυχαία στιγμή της κίνησης . Και ο λόγος είναι - όχι διότι ένα ευθύγραμμα κινούμενο υλικό σημείο δεν μπορεί να έχει στιγμιαία γωνιακή επιτάχυνση ως προς Ο ή στιγμιαία στροφορμή ως προς Ο - , αλλά διότι

α. η ροπή αδράνειας του συστήματος δεν είναι χρονικά σταθερή αλλά και

β. η στιγμιαία γωνιακή ταχύτητα του Σ δεν είναι ίση με τη στιγμιαία γωνιακή ταχύτητα του τροχού.

Ο νόμος πρέπει να εφαρμοστεί με τη μορφή τ = dL/dt.

Μια άλλη ΛΥΣΗ βασιζόμενη στον νόμο τ = Ια_γων .

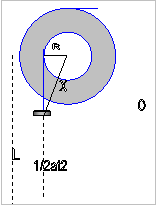
Καθώς το Σ ανεβαίνει επιταχυνόμενο η –ως προς Ο - ροπή αδράνειας mx ² μειώνεται αλλά και ο ρυθμός μεταβολής δεν είναι σταθερός. Για τη χρονική στιγμή που θα βρεθεί στο ύψος του Ο μπορούμε να αποδείξουμε ότι είναι η μόνη στιγμή στην οποία η ροπή αδράνειας έχει μηδενική παράγωγο. Με σύμβολα dI/dt = 0 .

Τη χρονική αυτή στιγμή – και μόνο αυτήν - μπορούμε να εφαρμόσουμε τον νόμο της στροφικής κίνησης για το σύστημα «στερεό Π, νήματα και σώμα Σ» με τη μορφή τ = Ια_γων

Τη στιγμή εκείνη – και μόνο τη στιγμή εκείνη - η ροπή αδράνειας του συστήματος είναι

ΜR² +mR² , η γωνιακή επιτάχυνση όλων των τμημάτων του κοινή, και ακόμα ισχύει α = α_γωνR

Οι παραπάνω σχέσεις σε συνδυασμό με την τιμή της ολικής ροπής τ = F.2R - mgR μας οδηγούν στο συμπέρασμα ότι η επιτάχυνση του Σ κατά τη στιγμή εκείνη είναι 1 m/s²

Δεδομένου ότι σε όλη κατά την ευθύγραμμη κίνηση του Σ οι ασκούμενες δυνάμεις βάρος και δύναμη του νήματος είναι σταθερές συνάγεται ότι σε όλη τη διάρκεια της κίνησης η επιτάχυνση είναι σταθερή. Άρα το αποτέλεσμα 1 m/s² αφορά στην επιτάχυνση της ευθύγραμμης ανοδικής κίνησης του Σ σε κάθε χρονική στιγμή.

Είναι μια λύση με μειονέκτημα το ότι χρειάζεται να γίνει αποδεκτό ή να αποδεχθεί ότι κατά τη στιγμή εκείνη dI/dt = 0

Μια απόδειξη μόνο για φυσικούς

Αν είναι L το συνολικό ύψος στο οποίο θα ανέβαινε το Σ

από την αρχική του θέση, όπου ήταν ακίνητο

μέχρι να φθάσει στο ίδιο ύψος με το Ο,

x η απόστασή του από το Ο σε τυχαία στιγμή t .

Η ροπή αδράνειας του Σ είναι Ι = mx² = m [R²+(L–½at²)²]

Ι = m [R²+L² +1/4 a²t⁴ – aLt²] dI/dt = mat(at²– 2L)

Η τιμή της dI/dt για t = √2L/a,

τη χρονική δηλαδή στιγμή που το Σ

έχει μετατοπιστεί κατά L, μηδενίζεται.

Πρόκειται βέβαια για μία λύση την οποία είναι απίθανο – κατά την άποψή μου - να επινοήσει ένας μαθητής. Ενώ αυτό που είναι πιθανό να κάνει είναι «εάν πάει η σκέψη του στο να εφαρμόσει τον νόμο τ = Ια_γων στο σύστημα να θεωρήσει - λανθασμένα – τη ροπή αδράνειας του Σ σταθερή και ίση με mR² .

Θα επιμείνω πάντως στο ότι η καλύτερη λύση

είναι με την εφαρμογή του γενικότερου νόμου τ = dL/dt στο σύστημα

Η λεγόμενη γενικότερη διατύπωση του δεύτερου νόμου για τη στροφική κίνηση

θα μπορούσε να αξιοποιηθεί περισσότερο κατά τη διδασκαλία μας. Στην τωρινή κατάσταση δεν φαίνεται η χρησιμότητά της. Ουσιαστικά δεν χρησιμοποιείται παρά μόνο

· για ερωτήσεις χωρίς καμία χρηστικότητα του τύπου «να υπολογίσετε τον ρυθμό μεταβολής της στροφορμής» με δεδομένα στοιχεία που οδηγούν στην τιμή της ολικής ροπής» και

· ως βάση για την παρουσίαση του νόμου διατήρησης της στροφορμής.

Βέβαια για να αξιοποιηθεί πρέπει να προηγηθεί η διδασκαλία

α. του ότι ένα υλικό σημείο «έχει» στροφορμή ως προς κάποιο Ο, ανεξάρτητα από «πώς» κινείται

β. του «ως προς τι είναι γενικότερη από την διατύπωση τ = Ια_γων.»

γ. του ότι ο νόμος αναφέρεται σε οποιοδήποτε σύστημα σωμάτων ανεξάρτητα από το είδος της κίνησης που εκτελούν τα τμήματά του.

Ένα παράδειγμα

Δύο σημειακά αντικείμενα Σ₁ και Σ₂ , μαζών m₁ και m₂ , προσδένονται στα άκρα αβαρούς νήματος διερχόμενου από ακίνητη 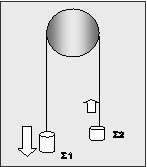τροχαλία, κέντρου Ο μάζας Μ και ακτίνας R , όπως στο σχήμα. Να υπολογίσουμε την τιμή της επιτάχυνσης καθενός. Για τη ροπή αδράνειας της τροχαλίας ως προς τον άξονα περιστροφής ισχύει Ι = ½MR².

Το πρόβλημα μπορεί να λυθεί αν εφαρμόσουμε

α. τον δεύτερο νόμο για την ευθύγραμμη κίνηση του Σ₁

β. τον δεύτερο νόμο για την ευθύγραμμη κίνηση του Σ₂.

γ . τον νόμο για τη στροφική κίνηση της τροχαλίας

και χρησιμοποιήσουμε τις έννοιες δύναμη του τεντωμένου νήματος στο Σ₁, δύναμη του τεντωμένου νήματος στο Σ₂, και δύναμη του τεντωμένου νήματος στην τροχαλία και τη σχέση α = α_γωνR, όπου α το μέτρο της επιτάχυνσης κάθε σώματος αλλά και της επιτρόχιας επιτάχυνσης των περιφερειακών σημείων της στρεφόμενης τροχαλίας.

Το ίδιο πρόβλημα όμως μπορεί να λυθεί και με το να εφαρμόσουμε τον νόμο της στροφικής κίνησης με τη γενικότερη διατύπωση

τ = dL/dt στο σύστημα «τροχαλία, Σ₁, Σ₂, νήμα». Οι ασκούμενες εξωτερικές δυνάμεις με ροπή ως προς Ο είναι μόνο τα βάρη m₁g και m₂g των δύο σωμάτων, άρα η ολική ροπή ως προς Ο είναι τ = (m₁g - m₂g)R .

Η ως προς Ο στροφορμή του συστήματος σε μια τυχαία στιγμή είναι m₁υR + m₂υR+ Ιω.

Άρα ο ρυθμός μεταβολής της στροφορμής είναι dL/dt = m₁aR + m₂aR+ Ιa_γων και εφόσον Ι = ½MR² και α = α_γωνR.

dL/dt = (m₁ + m₂+ ½Μ)Ra Σύμφωνα με τον νόμο (m₁+m₂+½Μ)Ra = (m₁g-m₂g)R α = (m₁-m₂)g /(m₁+m₂+½Μ) .

Ένα παράδειγμα και είναι από τα καλύτερα.

Σχετίζεται με ερώτηση που έκανε ο Ηλίας Δασκολιάς, τώρα φοιτητής, τότε μαθητής σε ώρα διαλείμματος. Και έκανε την ερώτηση με διστακτικό τρόπο, φοβούμενος ότι αυτό που λέει μπορεί και να είναι ανοησία.

Κύριε . . . .όταν η χορεύτρια στον πάγο στρέφεται με τεντωμένα χέρια έχει ορισμένη γωνιακή ταχύτητα . . όταν μαζεύει τα χέρια της αυξάνεται η γωνιακή της ταχύτητα. Αυτό σημαίνει ότι εμφανίζεται κάποια γωνιακή επιτάχυνση; Και αν ναι . . . . .ξέρετε τι με δυσκολεύει;

Το να δώσω μια απάντηση στο ερώτημα:

ΕΙΝΑΙ ΔΥΝΑΤΟΝ ΝΑ ΕΧΕΙ ΓΩΝΙΑΚΗ ΕΠΙΤΑΧΥΝΣΗ ΧΩΡΙΣ ΝΑ ΑΣΚΟΥΝΤΑΙ ΕΞΩΤΕΡΙΚΕΣ ΔΥΝΑΜΕΙΣ ΜΕ ΚΑΠΟΙΑ ΡΟΠΗ ;

Δεν παραβιάζεται ο νόμος τ = Ι_αγων της στροφικής κίνησης ;

Το δικό μου σχόλιο

Πρόκειται για ΕΞΑΙΡΕΤΙΚΟ ερώτημα το οποίο ίσως έχει υποβληθεί – ή έχει μείνει στο υπόγειο των απωθήσεων - και από άλλους μαθητές της Γ΄Λυκείου. Με κανένα τρόπο το σχολικό βιβλίο δεν μπορεί να οδηγήσει στην απάντηση.

Ανδρέας Ιωάννου Κασσέτας