Οδηγίες Μαθημάτων

Ύλη και οδηγίες για την Πληροφορική Γυμνασίου 2023-2024
Δείτε την ύλη και τις οδηγίες για τη διδασκαλία του μαθήματος της Πληροφορικής σε όλους τους τύπους Γυμνασίων για το σχολικό έτος 2023-2024.
Εργαλεία για την Τάξη

Τεχνητή Νοημοσύνη Μηχανική Μάθηση
Λίστα με εφαρμογές που χρησιμοποιούν Τεχνητή Νοημοσύνη και Μηχανική μάθηση
Προγραμματισμός

Δραστηριότητες υπολογιστικής σκέψης για την «Ώρα του Κώδικα»
Διασκεδαστικές δραστηριότητες για εκμάθηση βασικών προγραμματιστικών δομών, με αφορμή την Ώρα του Κώδικα 2023!
Ασφάλεια στο Διαδίκτυο
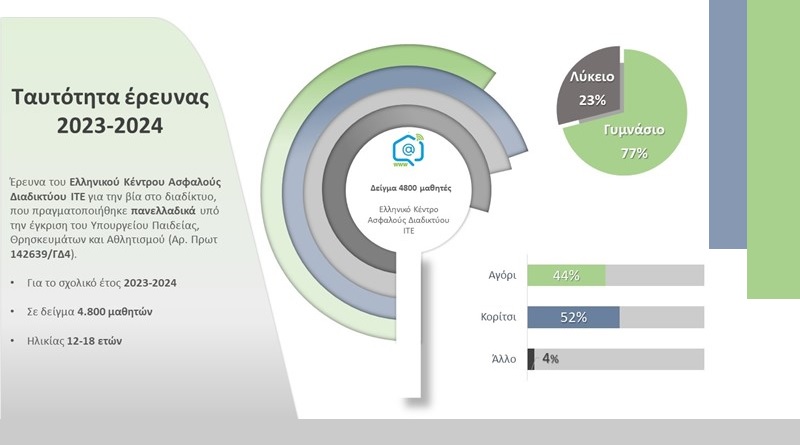
«Βία στο διαδίκτυο». Αποτελέσματα νέας πανελλήνιας έρευνας του Ελληνικού Κέντρου Ασφαλούς Διαδικτύου
Η έρευνα «Βία στο διαδίκτυο» πραγματοποιήθηκε κατά το διάστημα Νοέμβριος- Μάρτιος 2023-2024. Συμμετείχαν συνολικά 4.800 μαθητές ηλικίας 12 -18 ετών.