
η δεύτερη εξίσωση του συστήματος με τον μετασχηματισμό κ3 = w καταλήγει σε ένα τριώνυμο 2ου βαθμού:
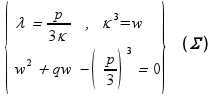
ΠΕΤΡΟΣ ΝΟΜΙΚΟΣ
Πολυωνυμικές Εξισώσεις 3ου και 4ου Βαθμού
Μου συνέβη το εξής: Συναντήθηκα, με τις συστάσεις ενός δασκάλου μου που τον θυμάμαι με σεβασμό, πολύ νωρίς με το Θεμελιώδες Θεώρημα της Άλγεβρας – από τα μαθητικά μου ήδη χρόνια – και επομένως με το πρόβλημα της επίλυσης των πολυωνυμικών εξισώσεων. Από τότε γνωρίζω ότι υπάρχει γενικός τρόπος επίλυσης των εξισώσεων 3ου και 4ου βαθμού, αλλά όσο ήμουν στα θρανία, ποτέ δεν έμαθα ποιος ήταν αυτός. Έτσι σαν παλιό χρέος προς τον εαυτό μου παρά σαν παρακαταθήκη για τους μαθητές μου συμμάζεψα το ιστορικό μαζί με το τεχνικό μέρος της γενικής επίλυσης των εξισώσεων 3ου και 4ου βαθμού που ακολουθεί. Ελπίζω να μην είναι πολύ βαρετό για όποιον θα είχε την περιέργεια.
(Scipione del Ferro (1465 – 1526))
Εξετάζουμε πρώτα την ανηγμένη μορφή μιας κυβικής εξισώσεως : x3 + px + q = 0 (Ε) .
Η κεντρική ιδέα βρίσκεται
στην ταυτότητα (κ – λ)3 = κ3
– 3κ2λ + 3κλ2 – λ3 που
γράφεται και ως (κ – λ)3 + 3κλ( κ –
λ) – (κ3 – λ3) = 0 και εάν
γράψεις x αντί για κ – λ παίρνεις την
x3 + 3κλ x – (κ3
– λ3) = 0 (*) που είναι
της ίδιας μορφής με την (Ε) και έχει ρίζα
την x = κ – λ .
Ας βρούμε λοιπόν κατάλληλα
κ , λ ώστε η (Ε) να πάρει την μορφή
(*). Εν τοιαύτη περιπτώσει θα πρέπει
οι αντίστοιχοι συντελεστές των δύο
αυτών πολυωνύμων να είναι ίσοι , δηλαδή
:
![]() Το σύστημα (σ) δίνει:
Το σύστημα (σ) δίνει:
η δεύτερη εξίσωση του συστήματος με
τον μετασχηματισμό κ3 = w καταλήγει
σε ένα τριώνυμο 2ου βαθμού:
![]() που
λέγεται Επιλύουσα της (Ε)
, και του οποίου ενδέχεται να χρειαστεί
να υπολογισθούν οι μιγαδικές λύσεις
στην περίπτωση που η διακρίνουσά της
είναι αρνητική. Τον υπολογισμό των κ
και λ περιγράφει το σύστημα:
που
λέγεται Επιλύουσα της (Ε)
, και του οποίου ενδέχεται να χρειαστεί
να υπολογισθούν οι μιγαδικές λύσεις
στην περίπτωση που η διακρίνουσά της
είναι αρνητική. Τον υπολογισμό των κ
και λ περιγράφει το σύστημα: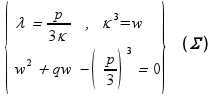
Οι άλλες ρίζες προκύπτουν ως ρίζες του δευτεροβάθμιου πηλίκου της διαίρεσης του πολυωνύμου της (Ε) διά του x - x0 .
(Nicolo Fontana Tartaglia (1500 – 1557))
Κάθε εξίσωση της μορφής ψ3
+ αψ2 + βψ + γ = 0 με α , β , γ
με α 0 παίρνει την
ανηγμένη μορφή (Ε) με τον μετασχηματισμό
:![]() .
.
Η πρόταση αυτή κλείνει το
θέμα της γενικής επίλυσης της κυβικής
εξίσωσης και την απόδειξή της δίνουμε
παρακάτω στην διερεύνηση της κυβικής
εξίσωσης.
Παρατήρηση
Εάν ο συντελεστής του τριτοβαθμίου όρου δεν είναι 1 , διαιρούμε την εξίσωση με αυτόν πριν εφαρμόσουμε τον μετασχηματισμό Tartaglia
Παράδειγμα : ψ3 + 3ψ2 + ψ + 3 = 0 (1)
θέτω
![]() (M) και μετά την αντικατάσταση , τα
αναπτύγματα και τις αναγωγές των ομοίων
όρων καταλήγουμε στην x3
– 2x + 4 = 0 (2) που είναι η ανηγμένη μορφή
της (1).
(M) και μετά την αντικατάσταση , τα
αναπτύγματα και τις αναγωγές των ομοίων
όρων καταλήγουμε στην x3
– 2x + 4 = 0 (2) που είναι η ανηγμένη μορφή
της (1).
Καταστρώνω το σύστημα (Σ) :
 Επιλύοντας το τελευταίο τριώνυμο
παίρνουμε
Επιλύοντας το τελευταίο τριώνυμο
παίρνουμε![]() ,
και ο μετασχηματισμός κ3 = w δίνει
,
και ο μετασχηματισμός κ3 = w δίνει

μία
λύση του συστήματος είναι η
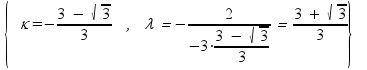
και μία λύση της (2) είναι η
![]()
Άρα
μία ρίζα της (1) βρίσκεται με αντικατάσταση
του x στον μετασχηματισμό
(Μ):
ψ = x0 – 1 = - 2 – 1 = -3 .
Τέλος
διαιρώντας το ψ3 + 3ψ2 + ψ + 3
διά ψ + 3 βρίσκω ψ2 + 1 .
Η
εξίσωση ψ2 + 1 = 0 είναι πλέον 2ου
βαθμού.
Η αρχή της περιπέτειας των πολυωνυμικών εξισώσεων χάνεται στα βάθη της ιστορίας . Ήδη οι Βαβυλώνιοι από το 5000 π.Χ. αλλά κυρίως μετά το 2000 π.Χ. γνώριζαν την επίλυση της πρωτοβάθμιας ενώ μπορούσαν να επιλύουν και ορισμένες μορφές της δευτεροβάθμιας. Οι Έλληνες με γεωμετρικό τρόπο και οι Άραβες πιο αλγεβρικά , αντιμετώπισαν τις δευτεροβάθμιες γενικά. Ο τρίτος βαθμός χρειάστηκε να περιμένει αρκετά.
|
Την επίλυση της ανηγμένης τριτοβάθμιας εξίσωσης x3 + px + q = 0 φαίνεται ότι την ανακάλυψε ο Scipione del Ferro (1465 – 1526), καθηγητής των μαθηματικών στο πανεπιστήμιο της Μπολόνια. Δεν κοινοποίησε αυτή του την ανακάλυψη ,παρά μόνο λίγο πριν από το θάνατό του, στον μαθητή του Antonio Maria Fior. Η ύπαρξη πάντως της ανακάλυψης του del Ferro έγινε γνωστή στην επιστημονική κοινότητα της Ιταλίας. Ο Fior πιστός στην μνήμη του δασκάλου του κρατούσε επίσης επτασφράγιστο το μυστικό. Στα 1530 ένας άλλος Ιταλός μαθηματικός , ο Nicolo Tartaglia (1500 – 1557) φαίνεται να γνωρίζει την επίλυση της |
|
ανηγμένης τριτοβάθμιας
εξίσωσης έχοντας εν τω μεταξύ ανακαλύψει
πώς να απαλλάσσεται από τον 2βάθμιο
όρο σε εξισώσεις της μορφής
x3
+ px2 + q = 0.
Το νέο διαδίδεται γρήγορα
και ο Fior υποπτεύεται λαθροχειρία εις
βάρος του δασκάλου του , και ίσως να
είχε δίκιο, αλλά υποτιμά τον Tartaglia και
τον καλεί δημοσίως να λύσουν τις
διαφορές τους με μία μαθηματική μονομαχία
: Ο καθένας τους δίνει 30 εξισώσεις στον
άλλο.
Ο Fior δεν είχε προχωρήσει πέρα
από τον δάσκαλό του και από τις
τριτοβάθμιες ήξερε να επιλύει μόνο την
ανηγμένη, ενώ ο Tartaglia αντιμετώπιζε ήδη
πιο γενικές εξισώσεις. Το αποτέλεσμα
της μονομαχίας είναι ισοπεδωτικό υπέρ
του Tartaglia: 30 – 0.
|
Τελικά ο Tartaglia θα φθάσει στην γενική επίλυση της τριτοβάθμιας γύρω στο 1541, εν τω μεταξύ όμως, ο θρίαμβός του επί του Fior συζητήθηκε ευρέως και τον Μάρτιο του 1539 ο Tartaglia δέχεται πρόσκληση ενός άλλου μαθηματικού , του Girolamo Cardano (1501 – 1576). Ο Gardano τον φιλοξενεί, τον κολακεύει και του υπόσχεται να τον παρουσιάσει σε κάποιον μαικήνα που θα του έλυνε τα χρόνια οικονομικά του προβλήματα. Έτσι ή αλλιώς , του απέσπασε πληροφορίες για την επίλυση της τριτοβάθμιας και δημοσιεύει τις νέες ανακαλύψεις στο βιβλίο του Ars Magna , το 1545 μαζί με την επίλυση της τεταρτοβάθμιας εξίσωσης που είχε στο μεταξύ |
|
(1540) επιτύχει ο μαθητής και γραμματέας του Ludovico Ferrari (1522 – 1565)
O Tartaglia , εξοργισμένος διαμαρτύρεται αλλά την υπεράσπιση του Cardano αναλαμβάνει ο Ludovico Ferrari , τα πράγματα αγρίεψαν, και λένε πως ο ατυχής Tartaglia φάνηκε εν τέλει τυχερός που βγήκε σώος από τα χέρια του Ferrari.
Οι ανακαλύψεις της Ιταλικής σχολής παρουσιάστηκαν οργανωμένες περιλαμβάνοντας και την πρώτη μελέτη μιγαδικών ριζών από τον Rafael Bombelli (1526 – 1573) στα 1572 με την έκδοση του βιβλίου του "Η Άλγεβρα".
Από τα 1572 πέρασαν 300 σχεδόν χρόνια , μελετήθηκαν συστηματικά οι μιγαδικοί αριθμοί και εμφανίστηκε το Θεμελιώδες Θεώρημα της Άλγεβρας αλλά οι αναζητήσεις μιας γενικής λύσης για την εξίσωση 5ου Βαθμού έμειναν άκαρπες . Μία τέτοια γενική λύση νόμισε προς στιγμήν ότι βρήκε ο Niels Henrik Abel (1802 – 1829), γρήγορα όμως ανακάλυψε λάθος στους συλλογισμούς του. Πείστηκε ότι η γενική λύση της εξίσωσης 5ου βαθμού είναι αδύνατη , πράγμα που απέδειξε τελικά το 1826. Από αυτό προκύπτει ότι είναι επίσης αδύνατη η γενική λύση των εξισώσεων βαθμού μεγαλύτερου από 4 (αποδείξτε το με εις άτοπον απαγωγή)
Αυτή ήταν και η τελευταία πράξη της μεγάλης περιπέτειας της αναζήτησης γενικής λύσης για τις πολυωνυμικές εξισώσεις. Λεπτομερέστερη εξιστόρηση μπορεί να βρει ο αναγνώστης στο [2] της βιβλιογραφίας
Στην περίπτωση που έχουμε πραγματικούς συντελεστές ας προσπαθήσουμε να βρούμε συνθήκες για το είδος των ριζών της κυβικής εξίσωσης,
Ας ξεκινήσουμε
με την εύκολη κυβική εξίσωση x3
+ px = 0 και έστω
g(x) = x3 + px η
υποκειμένη συνάρτηση, η οποία είναι
περιττή, έχει δηλαδή κέντρο συμμετρίας
το Ο(0,0). Η εξίσωσή μας έχει οπωσδήποτε
την μηδενική λύση και ενδεχομένως άλλες
δύο : x3 + px = 0
x(x2 + p) = 0 {x =
0 ή x2 + p = 0} εάν προκύψουν από το
τριωνύμου x2 + p = 0. Η παράγωγος g'
της g : g'(x) = 3x2 + p. Εάν συνάρτησή μας
έχει ακρότατα αυτά θα βρίσκονται στις
ρίζες της εξίσωσης
3x2 + p = 0,
δηλαδή
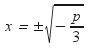 .
Ονομάζω
.
Ονομάζω
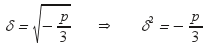 ,
οπότε οι θέσεις των ακροτάτων θα είναι
οι χ = δ και τα
ακρότατα (ένα μέγιστο και ένα ελάχιστο)
, τα g(δ) και g(-δ) .
,
οπότε οι θέσεις των ακροτάτων θα είναι
οι χ = δ και τα
ακρότατα (ένα μέγιστο και ένα ελάχιστο)
, τα g(δ) και g(-δ) .
Ονομάζω
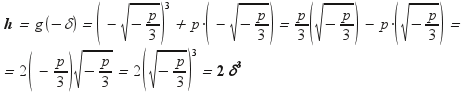
Στο σχήμα 1 φαίνονται τα δ και h
|
Σημειωτέον ότι το |h| παριστάνει την κατακόρυφη απόσταση του ακροτάτου από το Ο(0,0) όπου η γραφική παράσταση τέμνει τον άξονα y΄y Να παρατηρήσουμε τέλος ότι η ύπαρξη ακροτάτων είναι ισοδύναμη με την ύπαρξη πραγματικών λύσεων εκτός της μηδενικής: Καθένα από τα δύο ισοδυναμεί με την συνθήκη p < 0 ή για να χρησιμοποιήσουμε τα δ και h με την συνθήκη δ2 > 0 |
|
Ας προχωρήσουμε
τώρα στην ανηγμένη κυβική εξίσωση x3
+ px + q = 0 . Η υποκειμένη
συνάρτησή της είναι η f(x) = x3
+ px + q και προφανώς f(x) = g(x) + q δηλαδή η
γραφική παράσταση της f είναι η γραφική
παράσταση της g μετατοπισμένη κατά q
παράλληλα προς τον άξονα των y.
Είναι
εποπτικά φανερό (αλλά και εύκολα
αποδεικνύεται) ότι έχουμε πλέον ως
κέντρο συμμετρίας το σημείο Κ(0,q) και ο
ρόλος της απόλυτης τιμής του q στην
ύπαρξη λύσεων φαίνεται στα σχήματα 2,3
και 4.
Ας
επαναλάβουμε όμως την ίδια διαδικασία
όπως και με την συνάρτηση g προηγουμένως.
Για την συνάρτηση
f(x) = x3 + px + q
έχουμε: f ΄(x) = 3x2 + p.
Οι θέσεις των
ακροτάτων παραμένουν οι ίδιες και
εφόσον έχουμε g(x) = f(x) – q, η
|
ποσότητα h
= g(-δ)= f(-δ) – q είναι η διαφορά των
τεταγμένων του σημείου όπου η f τέμνει
τον y΄y από το τοπικό ακρότατο και
επομένως η |h| εκφράζει την κατακόρυφη
απόσταση των δύο.
|
|
Στα σχήματα 3 και 4 έχουμε |q| = |h| και 2 πραγματικές ρίζες (ή μία διπλή)
Στο σχήμα 5 έχουμε |q| = |h| και 1 μόνο πραγματική ρίζα
|
|
|
|
|
|
Μπορούμε
πλέον να καταστρώσουμε έναν γενικό
πίνακα για τις λύσεις της ανηγμένης
τριτοβάθμιας εξίσωσης με πραγματικούς
συντελεστές , με τα αποτελέσματα που
προκύπτουν γεωμετρικά:
|
Διερεύνηση της κυβικής εξίσωσης |
||
|
δ |
q2 - h2 |
Πλήθος και είδος των ριζών |
|
|
|
1 πραγματική & 2 μιγαδικές |
|
δ > 0 |
q2 – h2 < 0 |
Τρεις πραγματικές ρίζες |
|
q2 – h2 = 0 |
2 Πραγματικές η μία διπλή |
|
|
1 πραγματική & 2 μιγαδικές |
||
Είναι
τώρα καιρός να δούμε εάν αυτά τα
συμπεράσματα μπορούν να εφαρμοστούν
στην γενική εξίσωση τρίτου βαθμού κατά
τρόπο αλγεβρικό, και να διαπιστώσουμε
εάν πράγματι η ποσότητα q2
– h2 εμφανίζεται.
Εφαρμόζουμε λοιπόν τον μετασχηματισμό
Tartaglia στην κυβική εξίσωση ψ3 +
αψ2 + βψ + γ = 0 .
Θέτω λοιπόν
![]() και
παίρνω την ανηγμένη (E)
και
παίρνω την ανηγμένη (E)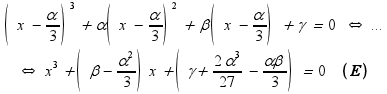
όπου
συγκρίνοντας με την μορφή x3
+ px + q = 0 έχουμε
![]()
Ας ξεκινήσουμε λοιπόν :
Το
δ θα είναι
επομένως πραγματικός αριθμός και
ορίζεται ως:

ενώ το h
θα είναι h = g(-δ) = 2δ3 (2)
όπως και προηγουμένως. Όπως είδαμε στην
επίλυση της ανηγμένης καταλήγουμε
τελικά στο σύστημα
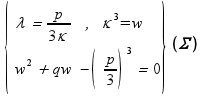
Η διακρίνουσα
της επιλύουσας είναι η
![]()
Πραγματικά λοιπόν η ποσότητα q2 – h2 που γεωμετρικά είδαμε ότι εκφράζει την κατακόρυφη απόσταση του ακροτάτου από το σημείο όπου η συνάρτηση f τέμνει τον άξονα y΄y, αλγεβρικά είναι η διακρίνουσα της επιλυούσης.
Το κρίσιμο σημείο είναι τώρα το πρόσημο της Δ:
Εάν Δ = q2 – h2 < 0 τότε η επιλύουσα έχει δύο συζυγείς μιγαδικές λύσεις
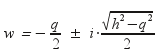 .
Έστω λοιπόν
.
Έστω λοιπόν
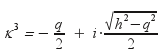
και
ας υπολογίσουμε το |κ|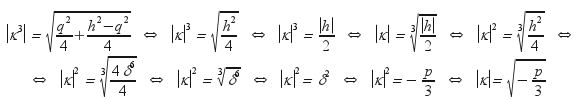
Το λ που θα
προκύψει από το σύστημα θα είναι το
συζυγές του αντιθέτου του κ .
Πράγματι
, έστω κ μία κυβική ρίζα του κ3 :
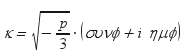
το
λ θα προκύψει από το σύστημα (Σ) ως
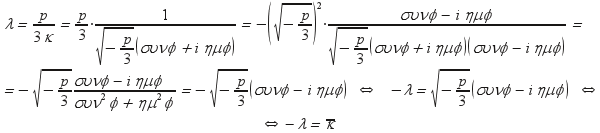
Επομένως η διαφορά κ – λ είναι
πραγματικός και μάλιστα
![]() όπου
όπου
![]() είναι
το πραγματικό μέρος του κ.
είναι
το πραγματικό μέρος του κ.
Εάν τώρα
διαιρέσουμε το x3 + px + q διά x – (κ
– λ) με την βοήθεια του σχήματος Horner:
|
1 |
0 |
p |
q |
(κ – λ) |
|
|
|
(κ – λ)2 |
p (κ – λ) + (κ – λ)3 |
|
|
1 |
κ - λ |
p + (κ – λ)2 |
q + p (κ – λ) + (κ – λ)3 |
|
παίρνουμε ως πηλίκον το τριώνυμο 2ου βαθμού : x2 + (κ – λ)x + p + (κ – λ)2 = 0, του οποίου η διακρίνουσα είναι Δ = (κ – λ)2 – 4(p + (κ – λ)2) = – 4p – 3(κ – λ)2 που είναι θετική. Πράγματι :
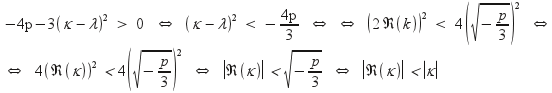
Η τελευταία ισότητα είναι αληθής: Το πραγματικό μέρος ενός γνησίου μιγαδικού είναι απολύτως μικρότερο από το μέτρο του.
Συνολικά λοιπόν τρεις πραγματικές ρίζες.
Εάν
Δ = q2 – h2 =
0 τότε q 0 , η επιλύουσα
έχει μία πραγματική ρίζα :![]() και
και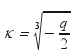 εάν q < 0 ή
εάν q < 0 ή
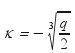 εάν
q > 0.
εάν
q > 0.
για q < 0
Από την συνθήκη Δ = q2 – h2 = 0 παίρνουμε
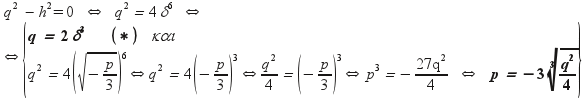
και το λ υπολογίζεται από το (Σ) ως εξής :

Μία ρίζα λοιπόν
της ανηγμένης είναι η κ – λ και διαιρώντας
την x3 + px + q διά
 με
το σχήμα Horner:
με
το σχήμα Horner:
|
1 |
0 |
|
q |
|
|
|
|
|
|
|
|
1 |
|
|
0 |
|
Παίρνω πηλίκον την δευτεροβάθμια
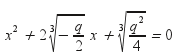 που
έχει διπλή ρίζα την
που
έχει διπλή ρίζα την
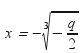 .
Αξίζει να σημειώσουμε ότι λόγω της (*)
η διπλή ρίζα
.
Αξίζει να σημειώσουμε ότι λόγω της (*)
η διπλή ρίζα
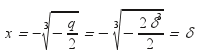 ενώ
η απλή θα είναι η x = –
2δ
ενώ
η απλή θα είναι η x = –
2δ
για
q > 0
Με την ίδια διαδικασία
υπολογίζουμε μία διπλή ρίζα , την x =
– δ και μία
απλή x = 2δ
Συνολικά λοιπόν δύο πραγματικές ρίζες η μία διπλή.
Εάν
Δ = q2 – h2
> 0 τότε η επιλύουσα έχει δύο πραγματικές
ρίζες. Η διακρίνουσά της είναι όπως
είδαμε
![]() ή
ή
![]()
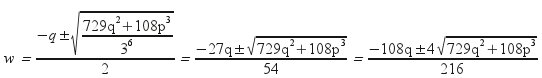 Επομένως
για
Επομένως
για
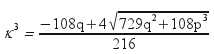 παίρνουμε
παίρνουμε
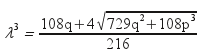 και
δεδομένου ότι p < 0 οι ρίζες είναι
ομόσημες και εάν q < 0 είναι θετικές ενώ
εάν q > 0 είναι αρνητικές ενώ από την
άλλη η εξίσωση
και
δεδομένου ότι p < 0 οι ρίζες είναι
ομόσημες και εάν q < 0 είναι θετικές ενώ
εάν q > 0 είναι αρνητικές ενώ από την
άλλη η εξίσωση
![]() μας
λέει ότι τα κ , λ είναι ετερόσημα, εάν
μεν q < 0 θα έχουμε
μας
λέει ότι τα κ , λ είναι ετερόσημα, εάν
μεν q < 0 θα έχουμε
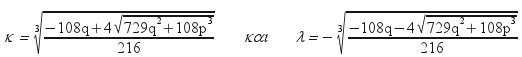
ενώ εάν q > 0

και
έτσι μία πραγματική ρίζα της ανηγμένης
θα είναι η
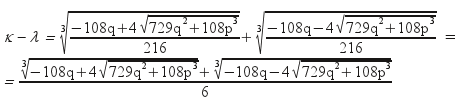
ενώ στην δεύτερη περίπτωση
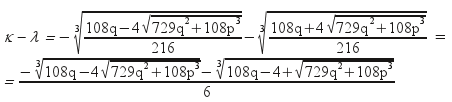
Στις δύο αυτές περιπτώσεις προκύπτουν λοιπόν αντίθετες τιμές για το κ – λ.
Είδαμε προηγουμένως
ότι το πηλίκον της διαίρεσης της
ανηγμένης x3 + px + q διά x – (κ-λ)
είναι x2 + (κ – λ)x + p + (κ – λ)2
, Θα δείξουμε το τριωνύμου αυτό δεν έχει
πραγματικές ρίζες δηλ. η ανηγμένη x3
+ px + q = 0 δεν έχει άλλη πραγματική ρίζα
και επομένως το ίδιο και η αρχική μας
ψ3
+ αψ2
+ βψ + γ = 0 . Θα δείξουμε δηλαδή ότι Δ <
0 ή
![]() Θα
υπολογίσουμε το (κ – λ)2.
Θα
υπολογίσουμε το (κ – λ)2.
Το
πρόσημο του κ – λ εφόσον τετραγωνίζεται
δεν έχει σημασία. Το αποτέλεσμα θα είναι
το ίδιο είτε q < 0 είτε q > 0.
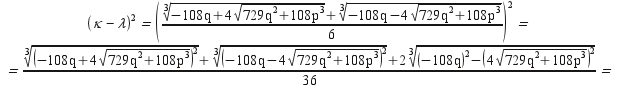
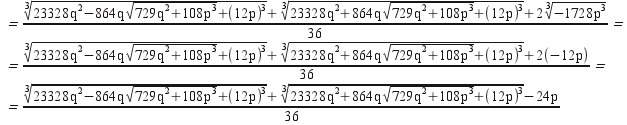
Αρκεί επομένως να αποδείξουμε σύμφωνα με την (Ζ) ότι

Εδώ μας χρειάζεται η ταυτότητα (a + b)3 = a3 + b3 + 3ab(a + b) όπου a και b είναι στην περίπτωσή μας οι δύο κυβικές ρίζες και δεδομένης της (*) αρκεί να αποδείξουμε ότι :
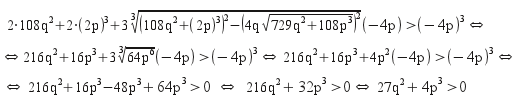
Η
τελευταία αυτή ανισότητα είναι αληθής
από την υπόθεση ότι η διακρίνουσα της
επιλυούσης είναι θετική.
Συνολικά λοιπόν μας προέκυψε μία μόνο πραγματική ρίζα και δύο μιγαδικές
Στην περίπτωση αυτή η διακρίνουσα της επιλυούσης είναι θετική και όπως στην υποπερίπτωση 1γ έχουμε μία πραγματική ρίζα και δύο μιγαδικές.
Ο πίνακας της διερεύνησης όπως τον καταστρώσαμε με βάση την γεωμετρική εικόνα της κυβικής συνάρτησης , επαληθεύθηκε
Ιδιαίτερη μνεία αξίζει στην υποπερίπτωση 1α. Είναι η μοναδική περίπτωση όπου η ανηγμένη κυβική εξίσωση (και επομένως και η ίδια η γενική κυβική εξίσωση) έχει 3 διακεκριμένες πραγματικές ρίζες, οι οποίες όμως για να υπολογισθούν χρειάζεται να υπερβούμε τους πραγματικούς υπολογίζοντας κυβικές ρίζες των μιγαδικών λύσεων της επιλυούσης. Η περίπτωση ονομάστηκε Casus Irreducibilis. Το γεγονός αυτό είναι εξαιρετικά σημαντικό. Από ιστορικής απόψεως είναι το έναυσμα της εισαγωγής και μελέτης των μιγαδικών αριθμών. Μέχρι τότε , μολονότι μιγαδικές (τις ονόμαζαν φανταστικές) λύσεις προέκυπταν στην επίλυση του δευτεροβαθμίου τριωνύμου (όταν η διακρίνουσά του είναι αρνητική) δεν τους είχε αποδοθεί ιδιαίτερη σημασία. Στην επίλυση της κυβικής οι «φανταστικές» λύσεις της επιλυούσης δίνουν «πραγματικές» λύσεις στην κυβική. Είναι δηλαδή η πρώτη φορά, που οι «φανταστικοί» αριθμοί περνούν το κατώφλι της πραγματικότητας. Και δεν θα μπορούσε παρά να γίνει αλλιώς , διότι η Casus Irreducibilis είναι αναπόδραστη:(πρβλ. Βιβλιογραφία [1]) Δεν είναι δυνατή η κατασκευή αλγεβρικού τύπου επίλυσης της κυβικής εξίσωσης που δεν θα προσφεύγει στην χρήση μιγαδικών !
Θα μπορούσε όμως να κατασκευασθεί μη αλγεβρικός τύπος επίλυσης της κυβικής εξίσωσης , με την χρήση των κυκλικών συναρτήσεων:
Χρησιμοποιούμε
τον τριγωνομετρικό μετασχηματισμό x
= 2δσυνθ
οπότε η ανηγμένη κυβική x3
+ px + q = 0 χρησιμοποιώντας την σχέση p
= -3δ2
γίνεται
8δ3συν3θ
– 3δ2
.2δσυνθ
+ q = 0
2δ3(4συν3θ
– 3συνθ) = – q Αλλά h = 2δ3
επομένως
![]() .
Όμως ο τύπος De Moivre
.
Όμως ο τύπος De Moivre
![]() δηλαδή
έχουμε
δηλαδή
έχουμε
![]() .
Η συνθήκη ύπαρξης λύσεων για την τελευταία
είναι
.
Η συνθήκη ύπαρξης λύσεων για την τελευταία
είναι
![]() και
επομένως η μέθοδος εφαρμόζεται στην
περίπτωση q2
– h2
< 0 ( Casus
Irreducibilis) και
στην περίπτωση q2
– h2
= 0.
και
επομένως η μέθοδος εφαρμόζεται στην
περίπτωση q2
– h2
< 0 ( Casus
Irreducibilis) και
στην περίπτωση q2
– h2
= 0.
H
![]() τώρα
, εάν
τώρα
, εάν
![]() με
με
![]() είναι
ισοδύναμη με την εξίσωση
είναι
ισοδύναμη με την εξίσωση
![]() και
αναζητώντας λύσεις στο διάστημα [0 , 2π]
βρίσκουμε 6 που ανά δύο διαφέρουν κατά
2π και δίνουν τα ίδια συνημίτονα οπότε
μένουν
οι εξής 3 :
και
αναζητώντας λύσεις στο διάστημα [0 , 2π]
βρίσκουμε 6 που ανά δύο διαφέρουν κατά
2π και δίνουν τα ίδια συνημίτονα οπότε
μένουν
οι εξής 3 :![]() επομένως
επομένως
![]() . Αυτές είναι διακεκριμένες εφόσον
. Αυτές είναι διακεκριμένες εφόσον
![]() και
και
![]() ,
δηλαδή εφόσον q2
– h2
< 0.
,
δηλαδή εφόσον q2
– h2
< 0.
Εάν
έχουμε q2
– h2
= 0 τότε
![]()
Η
περίπτωση
![]() σημαίνει ω
= 0 και
σημαίνει ω
= 0 και
δίνει
![]()
ενώ
η περίπτωση
![]() σημαίνει
σημαίνει
![]() και δίνει
και δίνει
![]() ,όπως
είδαμε και προηγουμένως.
,όπως
είδαμε και προηγουμένως.
Η ανηγμένη μορφή της τεταρτοβάθμιας είναι η x4 + Ax2 + Bx + Γ = 0 (Ε')
Η
κεντρική ιδέα εδώ είναι η συμπλήρωση
του τετραγώνου , ώστε το 1ο μέλος να πάρει
την μορφή
![]() .
Έτσι προχωρούμε ως εξής :
.
Έτσι προχωρούμε ως εξής :![]() .
Σ' αυτό το σημείο φαίνεται η ικανότητα
του Ferrari: Χρησιμοποιεί έναν βοηθητικό
άγνωστο δ ώστε να μετασχηματίσει το 1ο
μέλος σε τετράγωνο τριωνύμου.
.
Σ' αυτό το σημείο φαίνεται η ικανότητα
του Ferrari: Χρησιμοποιεί έναν βοηθητικό
άγνωστο δ ώστε να μετασχηματίσει το 1ο
μέλος σε τετράγωνο τριωνύμου.
![]() .
Χρειάζεται επομένως να προστεθεί και
στα δύο μέλη το
.
Χρειάζεται επομένως να προστεθεί και
στα δύο μέλη το
![]() και
η (Ε΄) γίνεται :
και
η (Ε΄) γίνεται :
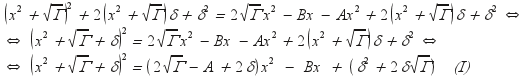
Αν το πρώτο μέλος είναι τέλειο τετράγωνο το ίδιο πρέπει να είναι και το δευτεροβάθμιο ως προς x τριώνυμο του 2ου μέλους , δηλαδή θα πρέπει η διακρίνουσά του να είναι μηδέν:
![]()
![]() .
Η εξίσωση αυτή είναι η επιλύουσα
της ανηγμένης και είναι 3ου βαθμού . Εάν
επιλυθεί κατά τα γνωστά θα βρούμε το δ
, την διπλή ρίζα του τριωνύμου του
δευτέρου μέλους της (Ι) και η (Ι) θα γραφεί
:
.
Η εξίσωση αυτή είναι η επιλύουσα
της ανηγμένης και είναι 3ου βαθμού . Εάν
επιλυθεί κατά τα γνωστά θα βρούμε το δ
, την διπλή ρίζα του τριωνύμου του
δευτέρου μέλους της (Ι) και η (Ι) θα γραφεί
:
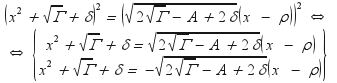 Από
τα δύο τελευταία τριώνυμα υπολογίζουμε
τις ρίζες της ανηγμένης τεταρτοβάθμιας.
Από
τα δύο τελευταία τριώνυμα υπολογίζουμε
τις ρίζες της ανηγμένης τεταρτοβάθμιας.
Παρατηρήσεις:
Εάν Γ < 0 τότε η τετραγωνική του ρίζα είναι φανταστικός αριθμός
Με τις κατάλληλες τροποποιήσεις (κυρίως στους συμβολισμούς) μπορούμε να εφαρμόσουμε την ίδια μέθοδο και σε πολυώνυμα με μιγαδικούς συντελεστές.
(Ludovico Ferrari)
Κάθε
εξίσωση της μορφής y4 + α y3
+ β y2 + γ y + δ = 0
![]() παίρνει την ανηγμένη μορφή (Ε') με τον
μετασχηματισμό :
παίρνει την ανηγμένη μορφή (Ε') με τον
μετασχηματισμό :![]() .
.
Η απόδειξη δίνεται στην επομένη παράγραφο
Παρατήρηση
Εάν ο συντελεστής του τεταρτοβαθμίου όρου δεν είναι 1 , διαιρούμε την εξίσωση με αυτόν πριν εφαρμόσουμε τον μετασχηματισμό Ferrari.
Ας θεωρήσουμε
την γενική εξίσωση τετάρτου βαθμού
y4
+ α y3 + β y2 + γ y + δ = 0 και
ας εφαρμόσουμε τον μετασχηματισμό
Ferrari:
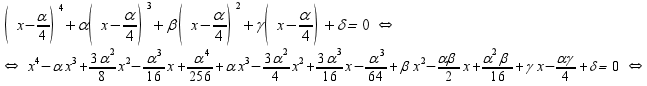
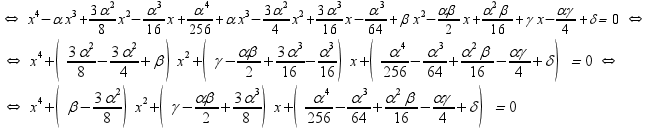
Η
τελευταία είναι η ανηγμένη της y4
+ α y3
+ β y2
+ γ y + δ = 0 και συγκρίνοντάς την με την
x4
+ Ax2
+ Bx + Γ = 0
![]()
Ας
ασχοληθούμε τώρα με την ανηγμένη x4
+ Ax2 + Bx + Γ = 0 και έστω
f(x)=x4 + Ax2 + Bx + Γ η υποκειμένη
συνάρτηση. Η παράγωγος της f είναι η
f΄(x)=4x3 + 2Ax + B τότε διαιρώντας
διά 4![]() η οποία έχει τις ίδιες ρίζες και πρόσημα
με την f ' και επιπλέον είναι μία ανηγμένη
κυβική της μορφής
η οποία έχει τις ίδιες ρίζες και πρόσημα
με την f ' και επιπλέον είναι μία ανηγμένη
κυβική της μορφής
x3 + px + q = 0 με
![]()
Οι κρίσιμοι αριθμοί δ
και h δίνονται από τις σχέσεις
 οπότε
οπότε
![]()
Είδαμε στην διερεύνηση της κυβικής ότι υπάρχουν τελικά 4 μορφές ανηγμένων κυβικών:
Εκείνες που δίνουν δ2 < 0 δηλαδή Α > 0 και έχουν μία μόνο πραγματική ρίζα
Εκείνες που δίνουν δ2 >
0 και q2 – h2 > 0 δηλαδή Α
< 0 και
![]() και
έχουν επίσης μία μόνο πραγματική ρίζα
και
έχουν επίσης μία μόνο πραγματική ρίζα
Εκείνες που δίνουν δ2 >
0 και q2 – h2 = 0 δηλαδή Α
< 0 και
![]() και
έχουν μία διπλή πραγματική ρίζα και
μία απλή επίσης πραγματική ρίζα
και
έχουν μία διπλή πραγματική ρίζα και
μία απλή επίσης πραγματική ρίζα
Εκείνες που δίνουν δ2 >
0 και q2 – h2 = 0 δηλαδή Α
< 0 και
![]() και
έχουν τρεις διακεκριμένες πραγματικές
ρίζες.
και
έχουν τρεις διακεκριμένες πραγματικές
ρίζες.
Ας εξετάσουμε κάθε περίπτωση ξεχωριστά :
Η f '/4 άρα
και η f ' έχει μόνο μία πραγματική ρίζα
xo και επομένως
f '(x) = 4(x –
xo)(x2+ax+b) όπου το τριώνυμο της
δεύτερης παρένθεσης έχει αρνητική
διακρίνουσα και είναι μονίμως
θετικό.
Ο πίνακας των μονοτονίας της
f είναι
|
|
|
xo |
|
Έχουμε λοιπόν ελάχιστο στη θέση xo και έστω m = f(xo) το ελάχιστο αυτό |
|
|
f ' |
– |
|
+ |
|
|
|
f |
|
|
|
|
|
Επειδή
![]()
|
Το θεώρημα Bolzano εν συνδυασμώ με την μονοτονία δίνει :
|
|
|
|
|
Στην περίπτωση
αυτή η f ' έχει επίσης μοναδική απλή
πραγματική ρίζα όπως και στην περίπτωση
1 αλλά εδώ η δεύτερη παράγωγος f '' έχει
δύο ρίζες. Έτσι η f έχει ένα και μόνο
τοπικό ελάχιστο m αλλά και δύο σημεία
καμπής στις θέσεις
 .
Ο αριθμός των ριζών της ανηγμένης
τεταρτοβάθμιας εξαρτάται και πάλι από
το πρόσημο του ελαχίστου.
.
Ο αριθμός των ριζών της ανηγμένης
τεταρτοβάθμιας εξαρτάται και πάλι από
το πρόσημο του ελαχίστου.
|
|
|
|
|
|
Στην περίπτωση
αυτή η f ' έχει μία απλή και μία διπλή
πραγματικές ρίζες, δηλαδή η f ' γράφεται
ως f
'(x) = 4(x – x1)2(x
– x2)
, ενώ η δεύτερη παράγωγος
f ''(x)=12x2 + 2A έχει δύο ρίζες τις
 που είναι και σημεία καμπής.
που είναι και σημεία καμπής.
Ο πίνακας μονοτονίας της f είναι ο ακόλουθος:
|
|
|
x2 |
|
Έχουμε λοιπόν ελάχιστο στη θέση x2 και έστω m = f(x2) το ελάχιστο αυτό |
|
|
f ' |
– |
|
+ |
|
|
|
f |
|
|
|
|
|
Έτσι η f έχει ένα και μόνο τοπικό ελάχιστο m αλλά και δύο σημεία καμπής στις θέσεις . Ο αριθμός των ριζών της ανηγμένης τεταρτοβάθμιας εξαρτάται και πάλι από το πρόσημο του ελαχίστου.
|
|
|
|
|
Περίπτωση 4
Α < 0 και
![]()
Στην περίπτωση
αυτή η f ' έχει 3 διακεκριμένες πραγματικές
ρίζες
x1 < x2 <
x3 , η παράγωγος της f γράφεται
f '(x) = 4(x – x1)(x – x2)(x – x3).
Ο πίνακας μονοτονίας της f είναι ο
ακόλουθος:
|
|
x1 |
x2 |
x3 |
|
Έχουμε λοιπόν
τοπικά ελάχιστα στις θέσεις x1
και x3 έστω m1 =
f(x1) και |
|||
|
f ' |
– |
+ |
|
– |
+ |
|
||
|
f |
|
|
|
|
|
|
||
Και σ' αυτήν την
περίπτωση έχουμε τα δύο γνωστά πλέον
σημεία καμπής
 .
Από τον πίνακα της μονοτονίας είναι
φανερό ότι Μ2 > m1 και
Μ2 > m3. Επομένως το πλήθος
των πραγματικών λύσεων της ανηγμένης
τεταρτοβάθμιας εξαρτάται από τους
συνδυασμούς προσήμων των τριών
τοπικών ακροτάτων
.
Από τον πίνακα της μονοτονίας είναι
φανερό ότι Μ2 > m1 και
Μ2 > m3. Επομένως το πλήθος
των πραγματικών λύσεων της ανηγμένης
τεταρτοβάθμιας εξαρτάται από τους
συνδυασμούς προσήμων των τριών
τοπικών ακροτάτων
|
m1 |
M2 |
m3 |
Πλήθος πραγματικών ριζών |
Σχήμα |
|
|
– |
– |
2 διακεκριμένες |
16 |
|
|
0 |
– |
2 απλές και μία διπλή |
17 |
|
– |
|
– |
4 διακεκριμένες |
18 |
|
|
+ |
0 |
2 απλές και μία διπλή |
19 |
|
|
|
+ |
2 απλές |
20 |
|
|
|
– |
2 απλές και μία διπλή |
21 |
|
0 |
+ |
0 |
2 διπλές |
22 |
|
|
|
+ |
1 διπλή |
23 |
|
|
|
– |
2 απλές |
24 |
|
+ |
+ |
0 |
1 διπλή |
25 |
|
|
|
+ |
καμμία |
26 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Περιεχόμενα
Γενική επίλυση πολυωνυμικών εξισώσεων 3ου και 4ου βαθμού 2
Η κυβική εξίσωση 2
Επίλυση της ανηγμένης κυβικής εξίσωσης 2
Πρόταση 1 2
Το ιστορικό 4
Η Γεωμετρική ερμηνεία της επίλυσης 5
Διερεύνηση 7
Συμπέρασμα 11
Τριγωνομετρική επίλυση της Casus Irreducibilis 11
Η τεταρτοβάθμια 12
Επίλυση της ανηγμένης τεταρτοβάθμιας 12
Πρόταση 2 12
Διερεύνηση της τεταρτοβάθμιας 13
Βιβλιογραφία
[1] Van der Waerden B.L. , Algebra I
[2] Collette J. P. , Histoire des Mathιmatiques
[3] Nickalls R.W.D. , A new approach to solving the cubic: Cardan's solution revealed Mathematical Gazette 77 (1993), 354-359.
[4] Stephenson G. , Mathematical Methods for Science Students