Α. Σύνθεση δύο αρμονικών ταλαντώσεων τις ίδιας συχνότηταςΈστω ένα σώμα κάνει ταυτόχρονα δύο αρμονικές ταλαντώσεις της ίδιας συχνότητας που περιγράφονται από τις παρακάτω εξισώσεις 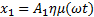

Παρατήρηση : Αν και οι δύο εξισώσεις παρουσιάζουν αρχική φάση μπορούμε να τις ανάγουμε στην παραπάνω περίπτωση με αλλαγή μεταβλητής ως εξής 
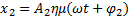
θέτοντας  τότε οι παραπάνω εξισώσεις γίνονται τότε οι παραπάνω εξισώσεις γίνονται 

η οποία είναι της ίδιας μορφής με τις αρχικές εξισώσεις Η απομάκρυνση του σώματος σε κάθε χρονική στιγμή θα είναι 

Η παραπάνω εξίσωση χρησιμοποιώντας τις γνώσεις από τα μαθηματικά ημ(α+β)=ημασυνβ+ημβσυνα 
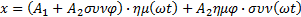
Η άλγεβρα Β λυκείου μας λέει ότι η συνάρτηση 
μπορεί να γραφεί με την μορφή 
όπου 
και φ μια γωνία που ικανοποιεί τις εξισώσεις 
οπότε στην δική μας περίπτωση η εξίσωση 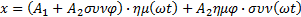
μπορεί να γραφεί με την μορφή 
όπου 
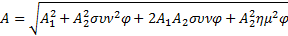
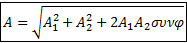 (1) (1)
και θ μια γωνία για την οποία 
Παρατήρηση : Συνηθίζουμε να υπολογίζουμε την εφφ. Όμως όποτε απλοποιούμε υπερβολικά τα μαθηματικά συχνά το πληρώνουμε με ασάφειες δηλαδή υπολογίζοντας την 
δεν μπορούμε να υπολογίσουμε την γωνία θ γιατί και η γωνία π+θ έχει την ίδια εφαπτομένη (εφ(π+θ)=εφθ) ενώ αν γνωρίζουμε το ημφ και το συνφ μπορούμε να προσδιορίσουμε το τεταρτημόριο στο οποίο ανήκει η γωνία
Το τελικό συμπέρασμα είναι ότι η σύνθεση δύο απλών αρμονικών ταλαντώσεων της ίδιας συχνότητας οδηγεί επίσης σε απλή αρμονική ταλάντωση της ίδιας συχνότητας. |