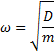Νοέ
02
2008
|
| |||
|
Πιέστε το πλήκτρο "Έναρξη" για να θέσετε το σώμα σε ταλάντωση. Με τα δύο διπλανά πλήκτρα βλέπετε καρέ καρέ την ταλάντωση. Μπορείτε να μεταβάλετε την σταθερά ταλάντωσης, την μάζα και την σταθερά απόσβεσης για να δείτε πως επιδρούν τα μεγέθη στην κίνηση του σώματος. Με δεξί κλικ στον χάρακα μπορείτε να το περιστρέψετε. Με Drag and Drop μπορείτε να μετακινήσετε τον χάρακα και το σώμα. Η Γεωμετρία (το αποτέλεσμα):Ας θυμηθούμε λίγα πράγματα από τις κινήσεις. Ευθύγραμμη ομαλή
α=0 Ευθύγραμμη ομαλά μεταβαλλόμενη
Θα γνωρίσουμε τώρα ένα νέο είδος κίνησης την απλή αρμονική ταλάντωση. Στην κίνηση αυτή οι εξισώσεις που περιγράφουν την κίνηση είναι
Οι παράμετροι Α,ω είναι θετικοί αριθμοί και Ωραίες οι εξισώσεις αλλά τι είδους κίνηση είναι αυτή; Την ευθύγραμμη ομαλή και την ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση τις γνωρίζουμε. Ας δούμε πως κινείται ένα σώμα όταν κάνει απλή αρμονική ταλάντωση. Παρατηρούμε ότι το σώμα πηγαινοέρχεται μεταξύ δύο ακραίων θέσων συμετρικές ως προς το μέσο Ο του ευθύγραμμου τμήματος ΒΓ. Η απόσταση από το μέσο Ο μέχρι το άκρο Β (ή Γ) ονομάζεται πλάτος της ταλάντωσης και συμβολίζεται με Α (ο συντελεστής στην εξίσωση (1)). (ΟΒ)=(ΟΓ)=Α=Πλάτος Ταλάντωσης. Ας δούμε άλλο ένα παράδειγμα. Παρατηρώντας τις δύο ταλαντώσεις βλέπουμε πως και οι δύο έχουν το ίδιο πλάτος αλλά σε κάτι διαφέρουν ... Η διαφορά τους είναι ότι το δεύτερο σώμα χρειάζεται περισσότερο χρόνο για να κάνει την κίνηση Ο?Γ?Ο?Β?Ο (μια πλήρες ταλάντωση). Ή αν θέλουμε το πρώτο περνάει πιο "συχνά" από το κέντρο Ο. Η διαφορά αυτή περιγράφεται με το μέγεθος ω στην εξίσωση (1). Το μέγεθος αυτό στην Φυσική το ονομάζουμε γωνιακή συχνότητα και συμβολίζεται με ω. Παρεμβολή : Τα μαθητικά λένε πως η συνάρτηση Για την δική μας εξίσωση (1) η περίοδος αντιπροσωπεύει τον χρόνο για μια πλήρη ταλάντωση.
και το αντίστροφο της περιόδου ονομάζεται συχνότητα f
Η συνάρτηση
ονομάζεται φάση και το φ0 ονομάζεται αρχική φάση. Από την εξίσωση (1) αν θέσουμε t=0 προκύπτει x(0)=Αημ(φ0) Η αρχική φάση φ0 καθορίζει το που βρίσκεται το σώμα την χρονική στιγμή t=0. Στην περίπτωση που για t=0 το σώμα βρίσκεται στην θέση x=0 και έχει θετική ταχύτητα τότε και μόνον τότε η φάση φ0 είναι μηδενική και οι εξισώσεις γίνονται
Η δυναμική (το αίτιο) :Μέχρι στιγμής μιλήσαμε για το πότε ένα σώμα εκτελεί απλή αρμονική ταλάντωση αλλά όχι τι αναγκάζει να εκτελέσει ένα σώμα απλή αρμονική ταλάντωση. Γνωρίζουμε πως όταν ένα σώμα εκτελεί ευθύγραμμη ομαλή κίνηση η τότε η συνισταμένη δύναμη είναι μηδέν καθώς επίσης και το αντίστροφο δηλαδή αν η συνισταμένη των δυνάμεων είναι μηδέν τότε η κίνηση είναι ευθύγραμμη ομαλή (γενικότερα δεν αλλάζει η ταχύτητα). Ενώ όταν ένα σώμα εκτελεί ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση τότε η συνισταμένη δύναμη είναι σταθερή. Ισχύει και το αντίστροφο δηλαδή αν συνισταμένη δύναμη είναι σταθερή τότε η κίνηση είναι ευθύγραμμα ομαλά μεταβαλλόμενη (με την προϋπόθεση η αρχική ταχύτητα να έχει την ίδια διεύθυνση με την συνισταμένη δύναμη). Τι γίνεται στην περίπτωση που ένα σώμα εκτελεί απλή αρμονική ταλάντωση;
Παρατηρούμε ότι η συνισταμένη δύναμη που ενεργεί σε σώμα που εκτελεί απλή αρμονική ταλάντωση είναι ανάλογη της απομάκρυνσης και έχει πάντοτε αντίθετη κατεύθυνση με αυτήν. Γι αυτό τον λόγο ονομάζεται και δύναμη επαναφοράς. η παράσταση
Είδαμε πως όταν το σώμα κάνει απλή αρμονική ταλάντωση ισχύει
ισχύει όμως το αντίστροφο; Δηλαδή αν η συνισταμένη των δυνάμεων είναι είναι Έτσι τελικά αν η συνισταμένη των δυνάμεων που ενεργούν σε ένα σώμα είναι της μορφής
τότε το σώμα θα εκτελέσει απλή αρμονική ταλάντωση με γωνιακή συχνότητα
Παρατήρηση :Ας συγκρίνουμε τις εξισώσεις Η ενέργεια (Γίνεται φυσική χωρίς ενέργεια και ορμή;) :Δυναμική ενέργεια έχει νόημα για συντηρητικές δυνάμεις, για δυνάμεις δηλαδή που το έργο τους είναι ανεξάρτητο από την διαδρομή : Η εξίσωση ορισμού της δυναμικής ενέργειας είναι
Στην περίπτωση που η δύναμη είναι της μορφής F=-Dx το έργο της δύναμης από x1 σε x2 θα είναι
δηλαδή η δυναμική ενέργεια θα δίνεται από την εξίσωση
Η κινητική ενέργεια του σώματος που εκτελεί απλή αρμονική ταλάντωση είναι
Το άθροισμα της κινητικής και δυναμικής ενέργειας είναι σταθερή και ίση με την ενέργεια στην ταλάντωση
Η παραπάνω εξίσωση αντιπροσωπεύει τη μέγιστη δυναμική ενέργεια που μπορεί να έχει το σώμα και αντιστοιχεί στην θέση μέγιστης απομάκρυνσης στην οποία η ταχύτητα άρα και η κινητική ενέργεια θα είναι μηδέν. Επίσης η παραπάνω εξίσωση μπορεί να μετασχηματιστεί ως εξής
Δηλαδή η ολική ενέργεια που έχει ένα σώμα όταν κάνει απλή αρμονική ταλάντωση είναι σταθερή και ίση είτε με την μέγιστη δυναμική είτε με την μέγιστη κινητική. Η δυναμική και η κινητική ενέργεια μπορούν να εκφραστούν σε συνάρτηση με τον χρόνο ως εξής
και η κινητική :
Από τα μαθηματικά :
οπότε η δυναμική και κινητική ενέργεια γίνονται
Από την παραπάνω εξίσωση προκύπτει ότι η δυναμική ενέργεια είναι περιοδική μεν αλλά με περίοδο ίση με την μισή της περιόδου ταλάντωσης του σώματος.
Όμοια και η κινητική ενέργεια
Για να κάνουμε την γραφική παράσταση εργαζόμαστε όπως φαίνεται στο παρακάτω σχήμα
|
 Σχόλια Σχόλια |
|
|
|