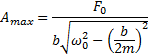Δεκ
06
2008
|
| |||
|
Στην παρακάτω προσομοίωση μπορείτε να μεταβάλετε τις διάφορες παραμέτρους για δείτε πως κινείται η σφαίρα. (Δοκιμάστε για b=0!) Στην περίπτωση της εξαναγκασμένης ταλάντωσης στο σώμα ενεργεί και μια επιπλέον περιοδική δύναμη της μορφής
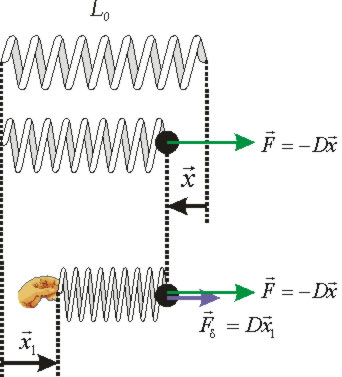
Ένας τρόπος να ασκήσουμε αυτήν την δύναμη είναι να αναγκάσουμε σε ταλάντωση το ένα άκρο του ελατηρίου ενώ στο άλλο άκρο είναι συνδεδεμένο το σώμα.
Ας δούμε γιατί. Αν το ελατήριο είναι παραμορφωμένο κατά
Αν τώρα προκαλέσουμε επιπλέον παραμόρφωση στο ελατήριο κατά
Αν το άκρο όπου ενεργεί ο διεργέρτης εκτελεί ταλάντωση
Ή διαφορετικά
   Η τελική εξίσωση που περιγράφει το φαινόμενο μαζί με την δύναμη τριβής θα είναι
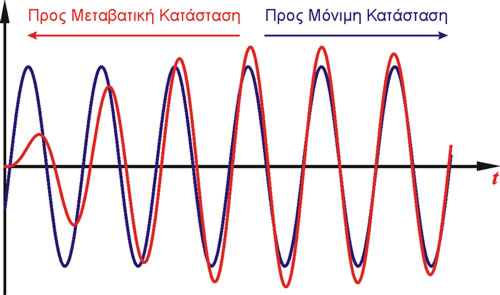
Το σώμα είναι καταδικασμένο μεν να εκτελέσει απλή αρμονική ταλάντωση με κυκλική συχνότητα ω όση και του διεγέρτη. Αυτό δεν θα συμβεί αμαχητί. Ο χρόνος που απαιτείται μέχρι το σώμα να περάσει από μια μεταβατική κατάσταση σε μια μόνιμη εξαρτάται από την σταθερά απόσβεσης b (όσο μικρότερη είναι τόσος μεγαλύτερος χρόνος απαιτείται).
Η μόνιμη κατάσταση περιγράφεται με την εξίσωση
όπου
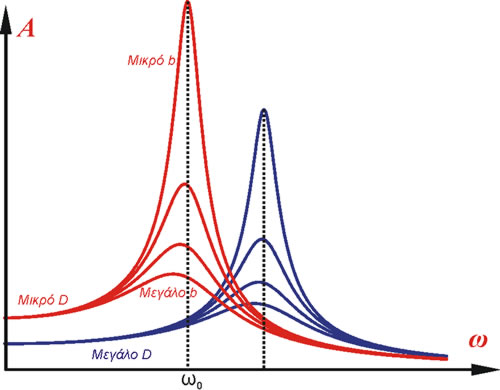
Ας εξετάσουμε πως μεταβάλλεται το πλάτος της ταλάντωσης σε σχέση με την κυκλική συχνότητα ω του διεγέρτη. Παρατηρούμε ότι αρχίζει από μια τιμή Για μεγάλες τιμές του ω το σώμα και ο διεγέρτης ταλαντώνονται με αντίθεση φάσης, έτσι η μία μετατόπιση σχεδόν αναιρεί την άλλη οπότε το σώμα ταλαντώνεται με πολύ μικρό πλάτος. όταν η συχνότητα του διεγέρτη γίνει ίση με την ιδιοσυχνότητα ταλάντωσης του συστήματος τότε το πλάτος της ταλάντωσης γίνεται πολύ μεγάλο. Για να είμαστε ακριβής όταν η η κυκλική συχνότητα του διεγέρτη γίνει ίση με
τότε το πλάτος της ταλάντωσης γίνεται μέγιστο και ίσο με
Για λόγους ευκολίας και χωρίς μεγάλο σφάλμα (ειδικά για μικρές τιμές του λόγου b/m) λέμε ότι το πλάτος γίνεται μέγιστο όταν η συχνότητα γίνει ίση με την ιδιοσυχνότητα του συστήματος. σε αυτήν την περίπτωση
Να σημειωθεί ότι σε αυτήν την περίπτωση έχουμε μέγιστη ταχύτητα χωρίς καθόλου σφάλμα.
Στην περίπτωση που Μια καλύτερη εποπτική εικόνα για την μεταβολή του πλάτους σε σχέση με διάφορες τιμές του D, b,ω φαίνεται στο παρακάτω διάγραμμα πλάτους - κυκλικής συχνότητας.
Ένα Πρόβλημα
Έχουμε δύο τέλεια ελαστικές μπάλες με ίσες μάζες. Η μία εκτελεί απλή αρμονική ταλάντωση και η άλλη εκτοξεύεται προς αυτήν που κάνει ταλάντωση. Σκοπός μας είναι να μεγιστοποιήσουμε το πλάτος της ταλάντωσης μετά την κρούση. α) Πώς πρέπει να γίνει η κρούση έτσι ώστε να πετύχουμε τον σκοπό μας; β) Πότε πρέπει να εκτοξεύσουμε την δεύτερη μπάλα για να συμβεί η κρούση στο επιθυμητό σημείο; (t=0 η στιγμή που αρχίζει η ταλάντωση, Δεδομένα: η κυκλική συχνότητα ταλάντωσης η απόσταση των σφαιρών οι ακτίνες τους και η ταχύτητα της δεύτερης σφαίρας.) Δοκιμάστε το με την προσομοίωση.
Την λύση του προβλήματος θα την βρείτε δημοσιευμένη με τίτλο "Λύση στο πρόβλημα Συντονισμού" (c) Σιτσανλής Ηλίας (Seilias) |
ασκεί δύναμη 
στο άλλο άκρο θα έχει ως αποτέλεσμα να ασκηθεί στο σώμα μια επιπλέον δύναμη της μορφής 
τότε η συνολική δύναμη που δέχεται το σώμα από το ελατήριο θα είναι 
(Στο δικό μας παράδειγμα 
οπότε η δύναμη που δέχεται το σώμα από τον διεγέρτη βρίσκεται πάντα σε φάση με την ταχύτητα. Τα διανύσματα δηλαδή της δύναμης του διεγέρτη και της ταχύτητας είναι πάντα ομόρροπα. Έτσι συνεχώς μεταφέρεται ενέργεια από την διεγέρτη στο σώμα με τον βέλτιστο τρόπο. Παρατηρείστε το πράσινο βελάκι που δείχνει την δύναμη που ασκεί ο διεγέρτης στο σώμα και το μπλε βελάκι που αντιπροσωπεύει την ταχύτητα.
 Σχόλια |
|
|
|