MATH PROJECT
Grade C, Junior
High school of Filiatra,
Messinia
School Year: 2004 - 05
Teacher name: Giannakopoulos Stamatis
Optional Math Project (to be
assigned as individual or group work).
Title: BRIDGE AT “
A daydreamer mechanic who is an
amateur mathematician as well as an admirer of beautiful “Stomio” beach in Filiatra Messinia, was excited
when a beautiful, sunny day in September he had the idea of constructing the
design of a straight-line bridge AB that
would connect the north site of the beach
A with the south site B and it
would be based on:
1)
two piers AA’ and BB’ of the ends A
and B (where A’ and B’ are the
points on the sea surface), and
2) a special metal, symmetrical, parabolic arc A’MB’ in arch-shape where M is
the mid point of the AB
bridge.
He also calculated that
in order for
the bridge to
be spectacular this
parabolic arc should be
the following: 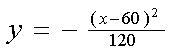
Where x is the horizontal distance in
meters measurement from point A
and y is
the vertical distance
in meters measurement from the straight line AA’.
To be calculated:
a) Produce such a
design including a relevant co-ordinate system.
b) Calculate the
AB bridge length.
c) Calculate the bridge height that extends over the
clear and crystalline waters
of “Stomio” beach.
Note 1: This project
should be handed in after the
end of Chapter
4 (page 125 of
the School book).
Note
2: This project should be printed with MS Word as
html file in
order for it
to be ready
for web-publishing. Digital
pictures of the
Stomio-beach area and /or relevant individual
or group
pictures may be
attached.
Date of project announcement:
Suggested date
to be handed in:
THE BEST ANSWER