Το  τρίγωνο  του  Sierpinski

   

    

    Ο  Πολωνός  μαθηματικός  Waclaw Sierpinski (1882-1969)  το  1915  εισήγαγε το παρακάτω
          φρακταλ, που φέρει το όνομα του και είναι ένα από τα πιο διάσημα  φράκταλ.

Για  την κατασκευή του τριγώνου του Sierpinski ακολουθούμε τα εξής βήματα.Αρχικά παίρνουμε ένα ισόπλευρο τρίγωνο (επίπεδο 0) ,ενώνουμε τα μέσα των πλευρών του και αφαιρούμε το μεσαίο τρίγωνο που σχηματίζεται,έτσι προκύπτει το σχήμα στο (επίπεδο 1) το οποίο αποτελεί  το βασικό μοτίβο. Στη συνέχεια σε κάθε ένα από τα τρία τρίγωνα που σχηματίζονται κάνουμε το ίδιο και παίρνουμε το  επόμενο σχήμα  (επίπεδο 2). Σε κάθε τρίγωνο τώρα του επιπέδου 2 κάνουμε το ίδιο κ.ο.κ.Στο παρακάτω applet μπορείτε να κατασκευάσετε μέχρι 10 επίπεδα του φράκταλ.
 

 

 

Από κάθε τρίγωνο του Sierpinski  παράγονται  Μ=3  μικρότερα κατά κλίμακα  r=1/2 .

Ο λόγος 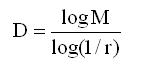  λέγεται διάσταση ομοιότητας του φράκταλ  και στην περίπτωση μας είναι D=1,584
 

Το τρίγωνο  του Sierpinski μπορούμε να το κατασκευάσουμε και με τον εξής τρόπο.
(Τάσος Μπουντής.Ο θαυμαστός κόσμος των Fractal  σελ 200) .

Παίρνουμε ένα τετράγωνο και εφαρμόζουμε σε αυτό τους παρακάτω τρείς γεωμετρικούς μετασχηματισμούς (Μαθηματικά Γ-Λυκείου σελ 37)

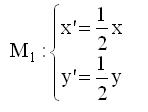Στη συνέχεια σε κάθε τετράγωνο που προκύπτει εφαρμόζουμε επίσης τους ίδιους μετασχηματισμούς κ.ο.κ.Τελικά θα προκύψει το τρίγωνο του Sierpinski.

Στο παρακάτω applet μπορείτε να κατασκευάσετε μέχρι 10 επίπεδα του φράκταλ

 

Με  το τρίγωνο του Sierpinski συμβαίνει κάτι το εκπληκτικό .Παίρνουμε στο εσωτερικό ενός  ισοπλεύρου τριγώνου ΑΒΓ ένα σημείο  Ρ0 , ρίχνουμε ένα ζάρι και αν το αποτέλεσμα είναι 1ή 2 ενώνουμε το σημείο με την κορυφή Α του τριγώνου (όπως στο παράδειγμα μας) ,αν είναι 3 ή 4 με την Β ενώ αν είναι 5 ή 6 με την Γ στη συνέχεια βρίσκουμε το μέσο του τμήματος Α Ρ0 . Θεωρούμε τώρα ως αρχικό σημείο το Ρ1  , ρίχνουμε ξανά το ζάρι και ας υποθέσουμε ότι έρχεται 3,ενώνουμε λοιπόν το Ρ1 με το Β και βρίσκουμε το μέσο του ΒΡ1,συνεχίζουμε  τη διαδικασία άπειρες φορές .Τι σχήμα θα σχηματίσουν το σημεία  Ρ0, Ρ1 ,Ρ2 , Ρ3 ,.......;
Με τη παρακάτω εφαρμογή μπορείτε να εκτελέσετε  το παραπάνω πείραμα όσες φορές θέλετε.

Κάντε κλικ μέσα στο τρίγωνο για να ορίσετε  το αρχικό σημείο Ρ0 ,στη συνέχεια με τα κουμπιά "Με το Α" κ.τ.λ ενώνεται το σημείο   ή με το Α ή με το Β ή με το Γ .

Μπορείτε μέσα στο πεδίο κειμένου δίπλα στη λέξη "Επαναλήψεις" να εισάγετε ένα αριθμό και πατώντας  " Enter" στο πληκτρολόγιο σας θα αρχίσει αυτόματα η διαδικασία .
   
 
 

Επιστροφή