

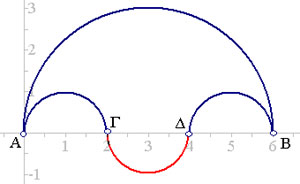
Στο παρακάτω σχήμα έχουμε ένα ημικύκλιο διαμέτρου ΑΒ=2ρ ,όπου ρ η ακτίνα του ημικυκλίου ,έχουμε διαιρέσει τη διάμετρο του σε τρία ίσα μέρη και έχουμε σχεδιάσει τα τρία ημικύκλια που φαίνονται στο σχήμα .
Το μήκος του ημικυκλίου είναι 2πρ:2=πρ.

Παρατηρούμε λοιπόν ότι: "Το μήκος του αρχικού ημικυκλίου είναι ίσο με το άθροισμα των μηκών των τριών μικρών ημικυκλίων"
Δηλ. αν έχουμε ένα ημικύκλιο και διαιρέσουμε τη διάμετρο του όπως παραπάνω, τότε το μήκος του είναι ίσο με το άθροισμα των μηκών των τριών μικρών ημικυκλίων. Αν διαιρέσουμε τώρα τη διάμετρο κάθε μικρού ημικυκλίου σε τρία ίσα μέρη και σχεδιάσουμε με τον ίδιο τρόπο τρία μικρότερα ημικύκλια στο εσωτερικό τους (άρα στο εσωτερικό του αρχικού θα σχεδιασθούν 9 μικρότερα ) τότε το μήκος του κάθε μικρού θα είναι ίσο με το μήκος των τριών μικρότερων ημικυκλίων που σχεδιάζονται στο εσωτερικό του και έτσι το μήκος του αρχικού ημικυκλίου θα είναι ίσο με το μήκος των 9 μικρότερων .(Πατήστε το πλήκτρο "Σχεδίασε" να σχεδιασθούν τα 9 ημικύκλια).Αν συνεχίσουμε με το ίδιο τρόπο στο επόμενο βήμα θα σχεδιασθούν 27 ημικύκλια με μήκος όσο το αρχικό. Έπειτα θα έχουμε 81 ημικύκλια (τα οποία σχεδιάζουμε λίγο πιο κάτω για να είναι εμφανή) και μετά 243 ημικύκλια. Παρατηρούμε όμως ότι τα ημικύκλια συνεχώς μικραίνουν και όταν γίνονται 243 ταυτίζονται με τη διάμετρο ΑΒ.
Άρα η διάμετρος ΑΒ είναι ίση με το μήκος του αρχικού ημικυκλίου!!!
Ερμηνεία Α: Προφανώς και η διάμετρος δεν είναι ίση με το ημικύκλιο. Αλλά καθώς αυξάνει ο αριθμός των ημικυκλίων η ακτίνα τους συνεχώς ελαττώνεται ,έρχεται λοιπόν κάποια στιγμή που γίνεται πολύ μικρή (μικρότερη π.χ από το pixel της οθόνης) ώστε τα ημικύκλια να μην μπορούν να σχεδιασθούν και φαίνεται να σχηματίζουν μια ευθεία γραμμή. Αν μεγεθύνουμε το σχήμα (πατήστε το πλήκτρο "Μεγέθυνση" (το πλήκτρο λειτουργεί μόνο στη περίπτωση των 243 ημικυκλίων) και στο παράθυρο που θα εμφανισθεί το "Μεγέθυνση" ) θα δούμε ότι τα ημικύκλια σχεδιάζονται κανονικά..
Ερμηνεία Β: Μπορεί κανείς να ισχυρισθεί ότι ,κάθε ημικύκλιο αποτελείται από τα άκρα του και το εσωτερικό του και όταν τα ημικύκλια τείνουν προς το άπειρο, τα άπειρα άκρα τους θα καλύψουν τα άπειρα σημεία του ευθυγράμμου τμήματος ΑΒ, ενώ τότε το εσωτερικό κάθε ημικυκλίου τείνει στο μηδέν άρα το άθροισμα των εσωτερικών των ημικυκλίων θα τείνει και αυτό στο μηδέν .Άρα τα ημικύκλια θα ταυτισθούν με την ΑΒ.
Ο ισχυρισμός όμως αυτός είναι λάθος και στα δυο του σκέλη.
Ας υποθέσουμε ότι το αρχικό ημικύκλιο βρίσκεται πάνω σε ένα σύστημα συντεταγμένων όπως στο σχήμα και έχουμε 3 μικρά ημικύκλια, τότε τα άκρα τους Α,Γ,Δ,Β βρίσκονται στα σημεία με συντεταγμένες 0,2,4,6.

Επομένων τα άκρα των άπείρων ημικυκλίων δεν θα καλύψουν τα σημεία της ΑΒ. Ο ισχυρισμός επίσης ότι το εσωτερικό των ημικυκλίων θα τείνει στο μηδέν είναι λάθος διότι τα ημικύκλια έχουν άπειρο το πλήθος. Και ενώ όταν έχουμε πεπερασμένες ποσότητες (π.χ 100) που κάθε μια τείνει στο μηδέν τότε και το άθροισμα τους θα τείνει στο μηδέν, αν οι ποσότητες είναι άπειρες δεν ισχύει αυτό. π.χ
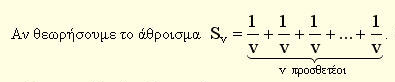
Τότε καθώς το ν τέινει στο άπειρο κάθε κλάσμα τείνει στο μηδέν ενώ το άθροισμα είναι ίσο με το ένα