

Η συνάρτηση y=αx+β
Όπως ξέρουμε για να σχεδιάσουμε τη γραφική παράσταση μιας συνάρτησης πρέπει να φτιάξουμε ένα πίνακα τιμών της.
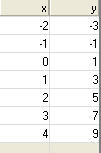
Στον πίνακα αυτό έχουμε δώσει στο x τις ακέραιες τιμές από -2 μέχρι το 4 δηλ -2≤ x ≤4 και η γραφική παράσταση που προκύπτει αποτελείται από τα κόκκινα σημεία του διπλανού σχήματος
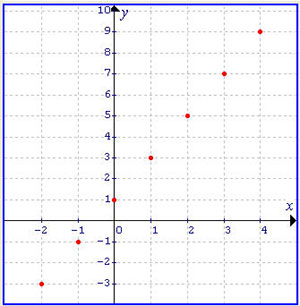
Γενικά κάθε συνάρτηση της μορφής y=αx+β με x πραγματικό έχει γραφική παράσταση ευθεία.
Με τη βοήθεια της παρακάτω εφαρμογής θα μελετήσουμε τη συνάρτηση y=αx+β για τις διάφορες τιμές των παραμέτρων α ,β και θα βγάλουμε χρήσιμα συμπεράσματα γι' αυτήν.
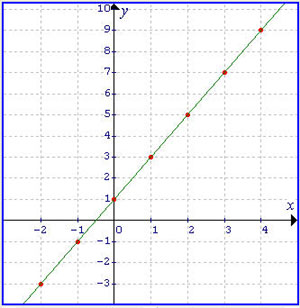
Η συνάρτηση αυτή προκύπτει από την y=αx+β αν δώσουμε στο α την τιμή 2 και στο β την 1.
Μπορούμε τώρα να κρατήσουμε το α σταθερό και να μεταβάλλουμε το β (δώστε νέα τιμή στο πεδίο δεξιά του "Τιμές :β" και πατήστε "Enter"),να κάνουμε δηλ τη γραφική παράσταση των συναρτήσεων y=2x-1 , y=2x-2 ,y=2x+3 κ.τ.λ
Κάνοντας αυτές τις γραφικές παραστάσεις παρατηρούμε ότι όλες οι ευθείες που προκύπτουν είναι μεταξύ τους παράλληλες
Άρα αν στην εξίσωση y=αx+β κρατήσουμε το α σταθερό και μεταβάλλουμε το β προκύπτουν ευθείες παράλληλες.
Πατήστε "Αναίρεση" κρατήστε το β σταθερό,δώστε νέες τιμές για το α και δείτε τι συμβαίνει.