ΘΕΩΡΗΜΑΤΑ
ROLLE
& ΜΕΣΗΣ ΤΙΜΗΣ
1.Διδακτικοι
Στόχοι :
Οι μαθητές :
2.
Διδακτικός χρόνος :
4 διδακτικές ώρες
3.
Σενάριο διδασκαλίας :



Σχήμα
1.
Στο σημείο αυτό ενθαρρύνουμε τους
μαθητές να αρχίσουν την έρευνα για την
εύρεση αναγκαίων συνθηκών, έτσι ώστε να
ισχύει αυτό το συμπέρασμα. Έτσι,
απευθύνουμε την εξής ερώτηση: « Είναι
δυνατόν να ισχύει η εικασία αυτή για
οποιαδήποτε καμπύλη;». Εάν κανένας μαθητής
δεν βρεθεί να υποδείξει
ότι η συνέχεια της συνάρτησης είναι μια
απαραίτητη προϋπόθεση, τότε μπορούμε να
ζητήσουμε από τους μαθητές να ζωγραφίσουν
τη γραφική παράσταση γνωστών συναρτήσεων,
όπως π.χ. της συνάρτησης f
:
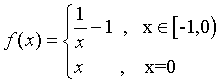
(σχήμα
2) και να ρωτήσουμε:
« Τι λέτε γι’ αυτή τη συνάρτηση, ισχύει η
παραπάνω εικασία;»
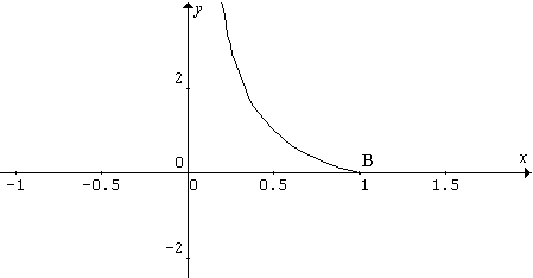
Σχήμα
2

Σχήμα 3
Το παράδειγμα αυτό δείχνει ότι πρέπει να συμπεριλάβουμε στην υπόθεση και τη συνθήκη της παραγωγισιμότητας της συνάρτησης στο πεδίο ορισμού της. Το ότι η συνθήκη της παραγωγισιμότητας είναι αναγκαία, θα φανεί λογικό στους μαθητές εάν τους προκαλέσουμε να βρουν και να ζωγραφίσουν μια συνεχή καμπύλη, για την οποία το συμπέρασμα του θεωρήματος δεν ισχύει. Η αδυναμία τους να βρουν μια τέτοια καμπύλη, αποτελεί μια ισχυρή διαισθητική βάση για να βελτιώσουν την αρχική διατύπωση του θεωρήματος – εικασία ως εξής: « Εάν μια συνάρτηση είναι συνεχής και παραγωγίσιμη στο πεδίο ορισμού της, τότε υπάρχει ένα τουλάχιστον σημείο της γραφικής της παράστασης στο οποίο η εφαπτομένη να είναι παράλληλη στον άξονα χ΄χ».
·
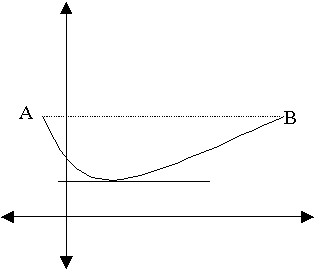
Με τη βοήθεια της γραφικής
παράστασης της συνάρτησης f
: ![]() (σχήμα 4),
(σχήμα 4),
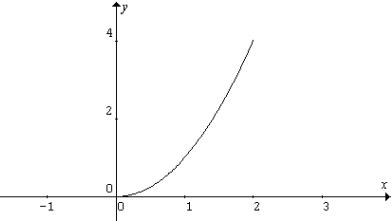
Σχήμα 4
· Διαπιστώνεται ότι συνθήκη f(α)=f(β) είναι ουσιαστική για να μπορεί να
εφαρμοστεί το θεώρημα στο διάστημα [α,β].
· Διατυπώνεται το τελικό πια θεώρημα του Rolle ως εξής: « Εάν μια συνάρτηση f είναι συνεχής στο [α,β] και παραγωγίσιμη στο (α,β), τότε υπάρχει ένα τουλάχιστον σημείο ξ στο διάστημα (α,β), τέτοιο ώστε η εφαπτομένη της γραφικής παράστασης στο σημείο (ξ,f(ξ)) να είναι παράλληλη στον άξονα χ΄χ».
·
Αφού φέρουμε στη μνήμη των
μαθητών τη γεωμετρική ερμηνεία της
παραγώγου και το συντελεστή διεύθυνσης
ενός ευθυγράμμου τμήματος, ζητάμε να
ξαναδιατυπωθεί το θεώρημα σε πιο τυπική
γλώσσα ως εξής: « Εάν η συνάρτηση f
είναι συνεχής στο [α,β] και παραγωγίσιμη στο
(α,β), τότε υπάρχει ένα σημείο ξ στο (α,β)
τέτοιο ώστε
![]() ».
».
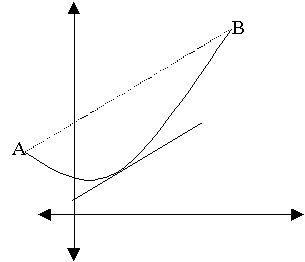
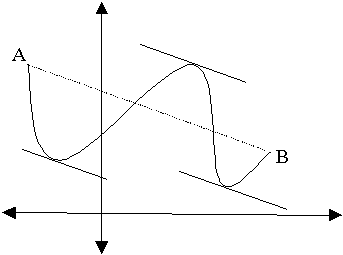
· Προκειμένου να συνδέσουμε το επόμενο θεώρημα της Μέσης τιμής με το θεώρημα του Rolle, μοιράζουμε στους μαθητές από ένα φύλλο στο οποίο παρουσιάζουμε τα προηγούμενα σχήματα, αφού πρώτα τα περιστρέψουμε κατά μια οξεία γωνία(σχήμα 5).
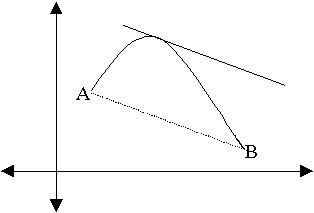
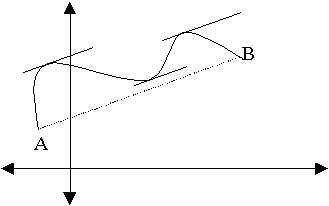
 σχήμα
5
σχήμα
5
Επειδή δεν αλλάζει τίποτε άλλο ως προς
τις προϋποθέσεις σχετικά με τις γραφικές
παραστάσεις των συναρτήσεων, εύκολα
οδηγούνται οι μαθητές στη διατύπωση
του θεωρήματος της Μέσης Τιμής, πρώτα σε
γεωμετρική γλώσσα: « Εάν μια
συνάρτηση f
είναι συνεχής στο [α,β] και παραγωγίσιμη στο
(α,β), τότε υπάρχει
τουλάχιστον ένα σημείο της γραφικής της
παράστασης στο οποίο η εφαπτομένη
είναι παράλληλη στη χορδή που συνδέει
τα άκρα της».
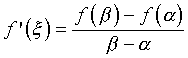 ».
».
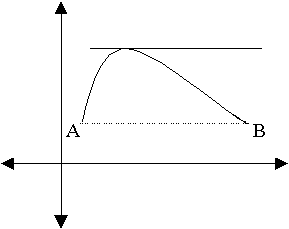
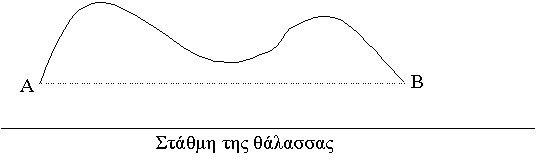
Στην πρώτη περίπτωση (σχήμα 6), έχουμε
ένα βουνό του οποίου οι
Πρόποδες Α και Β έχουν το ίδιο υψόμετρο
ως προς την οριζόντια στάθμη της
θάλασσας. Ένας ορειβάτης ξεκινά από
τους πρόποδες στο σημείο Α και
προσπαθεί να το ανέβει και στη συνέχεια
να το κατέβει, επιλέγοντας μια λεία
διαδρομή, ώσπου να φτάσει στους
πρόποδες από την άλλη όμως πλευρά του
στο σημείο Β. Το ερώτημα είναι εάν θα
υπάρξει τουλάχιστον κάποιο σημείο
της διαδρομής, στο οποίο ο ορειβάτης θα
βαδίζει ίσια, δηλαδή παράλληλα
προς την οριζόντια στάθμη της θάλασσας.
Η απάντηση είναι ότι αναγκαστικά αυτό
θα πρέπει να συμβεί, αφού σε
αντίθετη περίπτωση ο ορειβάτης θα
ανέβαινε διαρκώς, πράγμα που είναι
αδύνατο.
Σχήμα
6
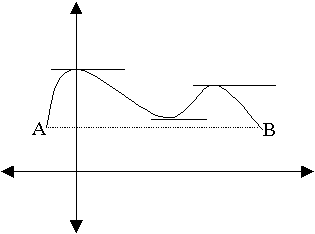
Στη δεύτερη περίπτωση(σχήμα 7), ο
ορειβάτης διασχίζει το βουνό ξεκινώντας
από τους πρόποδες στο σημείο Α και
καταλήγει στους πρόποδες
από την άλλη
μεριά στο σημείο Β το
οποίο βρίσκεται σε διαφορετικό υψόμετρο
από το
σημείο Α.
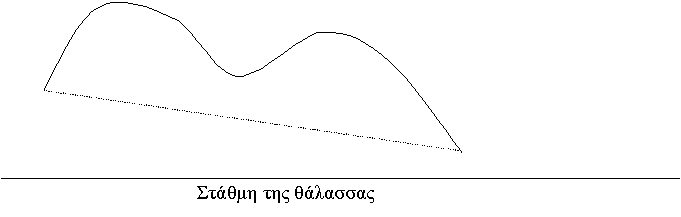
Σχήμα
7
Στο σημείο αυτό είναι δυνατό να χρησιμοποιηθεί κατάλληλο δυναμικό λογισμικό(π.χ. Sketchpad) προκειμένου να συνδεθεί το ομοίωμα του βουνούμε τη γραφική παράσταση μιας συνεχούς και παραγωγίσιμης συνάρτησης, ορισμένης σε διάστημα και να παραλληλιστεί η κατεύθυνση της κίνησης του ορειβάτη με την κατεύθυνση της εφαπτομένης κατά μήκος της γραφικής παράστασης(σχήμα 8-9)
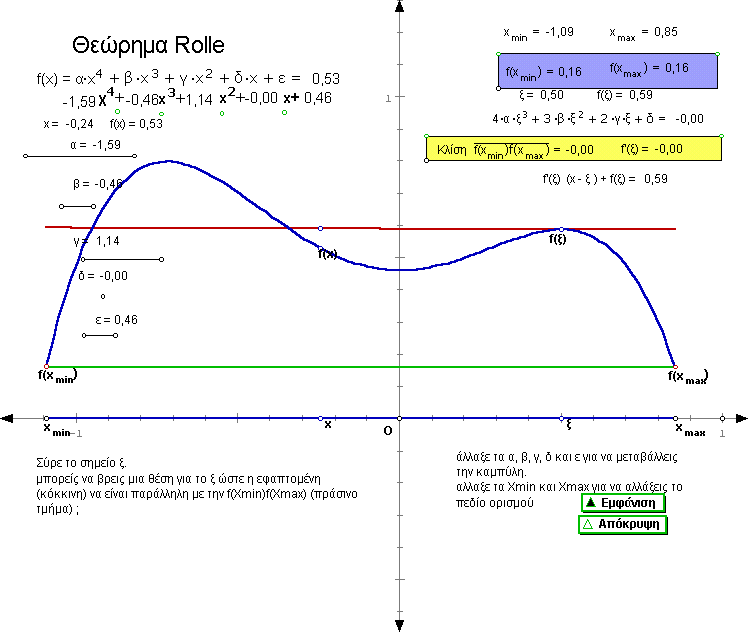
Σχήμα 8
(Το
αρχείο κατασκευάστηκε από το μαθηματικό
Τάσο Αρβανίτη)
Για
να δείτε αυτό το αρχείο κάνετε κλικ
εδώ
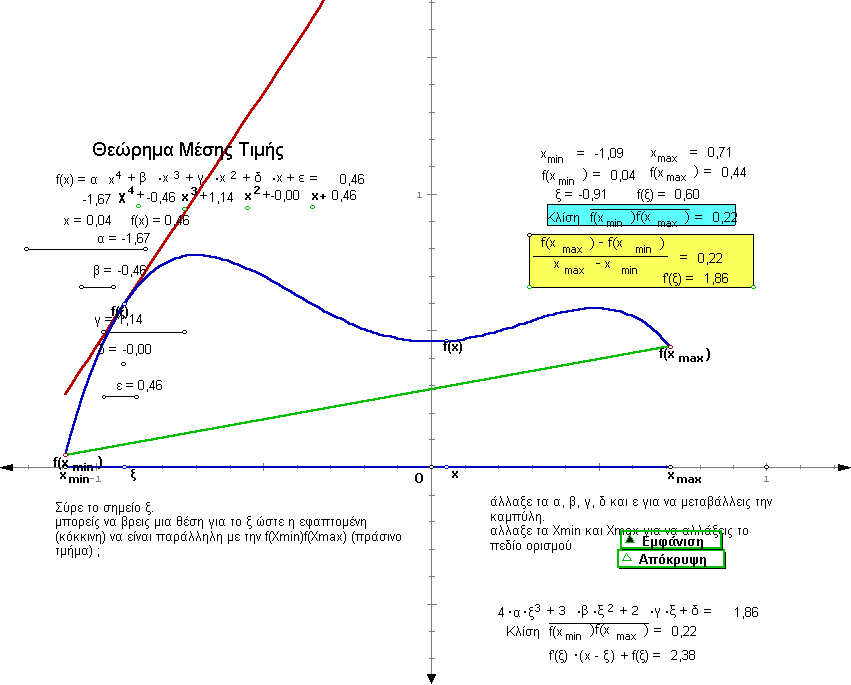
Σχήμα 9 (Το αρχείο κατασκευάστηκε από
τον Τάσο Αρβανίτη)
Για
να δείτε αυτό το αρχείο κάνετε κλικ
εδώ
·
Στη
συνέχεια παρουσιάζονται κάποιες βασικές
εφαρμογές αυτών των δύο θεωρημάτων σε
θέματα :
α) Ύπαρξης ρίζας της παραγώγου συνάρτησης
β) Ύπαρξης ρίζας συνάρτησης με τη βοήθεια
της αρχικής της
γ) Μοναδικότητας και πλήθους ριζών
συνάρτησης
δ) Ανισοτικών σχέσεων
© Μπάμπης Τουμάσης