ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ
Παράδειγμα 1.
Σώμα εκτελεί Α.Α.Τ. και η ταχύτητα μεταβάλλεται σύμφωνα με τη σχέση (S.I.)
(S.I.)
Να υπολογιστεί:
α. Η απόσταση των δύο ακραίων θέσεων
β. Η επιτάχυνση όταν η απομάκρυνση του σώματος είναι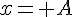
γ. Η ταχύτητα τη χρονική στιγμή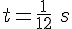
δ. Αν η μάζα του ταλαντούμενου σώματος είναι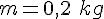 να υπολογιστεί η σταθερά επαναφοράς του συστήματος και ο ρυθμός μεταβολής της ορμής τη χρονική στιγμή όπου η απομάκρυνση είναι
να υπολογιστεί η σταθερά επαναφοράς του συστήματος και ο ρυθμός μεταβολής της ορμής τη χρονική στιγμή όπου η απομάκρυνση είναι 
Δίνεται και
και 
(ΘΕΜΑ Γ)
Σώμα εκτελεί Α.Α.Τ. και η ταχύτητα μεταβάλλεται σύμφωνα με τη σχέση
 (S.I.)
(S.I.)Να υπολογιστεί:
α. Η απόσταση των δύο ακραίων θέσεων
β. Η επιτάχυνση όταν η απομάκρυνση του σώματος είναι
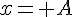
γ. Η ταχύτητα τη χρονική στιγμή
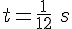
δ. Αν η μάζα του ταλαντούμενου σώματος είναι
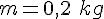 να υπολογιστεί η σταθερά επαναφοράς του συστήματος και ο ρυθμός μεταβολής της ορμής τη χρονική στιγμή όπου η απομάκρυνση είναι
να υπολογιστεί η σταθερά επαναφοράς του συστήματος και ο ρυθμός μεταβολής της ορμής τη χρονική στιγμή όπου η απομάκρυνση είναι 
Δίνεται
 και
και 
(ΘΕΜΑ Γ)
Λύση
Από την εξίσωση της ταχύτητας προκύπτει ότι:


Άρα
α. Επομένως οι δύο ακραίες θέσεις απέχουν
β. Όταν είναι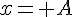 τότε
τότε 
γ. Τη χρονική στιγμή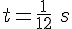 , η ταχύτητα είναι:
, η ταχύτητα είναι:
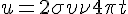



δ. Η σταθερά επαναφοράς υπολογίζεται από τη σχέση:
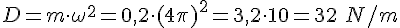
Ο ρυθμός μεταβολής της ορμής είναι ίσος με τη δύναμη επαναφοράς

Από την εξίσωση της ταχύτητας προκύπτει ότι:


Άρα

α. Επομένως οι δύο ακραίες θέσεις απέχουν

β. Όταν είναι
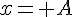 τότε
τότε 
γ. Τη χρονική στιγμή
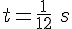 , η ταχύτητα είναι:
, η ταχύτητα είναι: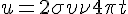



δ. Η σταθερά επαναφοράς υπολογίζεται από τη σχέση:
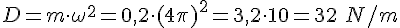
Ο ρυθμός μεταβολής της ορμής είναι ίσος με τη δύναμη επαναφοράς

Παράδειγμα 2.
Σώμα εκτελεί Α.Α.Τ.
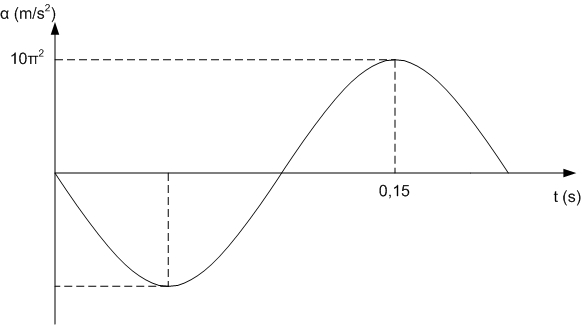
Στο παρακάτω σχήμα φαίνεται η γραφική παράσταση επιτάχυνσης-χρόνου
Να υπολογιστούν:
α. Το πλάτος της ταλάντωσης
β. Η συχνότητα και η γωνιακή συχνότητα
γ. Να βρεθεί η εξίσωση ταχύτητας-χρόνου και να σχεδιαστεί το αντίστοιχο ποσοτικό διάγραμμα
δ. Να κάνετε το διάγραμμα επιτάχυνσης-απομάκρυνσης (ποσοτικό)
(ΘΕΜΑ Γ)
Σώμα εκτελεί Α.Α.Τ.
Στο παρακάτω σχήμα φαίνεται η γραφική παράσταση επιτάχυνσης-χρόνου

Να υπολογιστούν:
α. Το πλάτος της ταλάντωσης
β. Η συχνότητα και η γωνιακή συχνότητα
γ. Να βρεθεί η εξίσωση ταχύτητας-χρόνου και να σχεδιαστεί το αντίστοιχο ποσοτικό διάγραμμα
δ. Να κάνετε το διάγραμμα επιτάχυνσης-απομάκρυνσης (ποσοτικό)
(ΘΕΜΑ Γ)
Λύση
Από το διάγραμμα προκύπτει ότι:
 και
και 
α.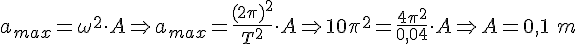
β.

γ.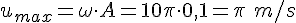
Άρα η εξίσωση της ταχύτητας είναι:

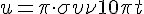 (S.I.)
(S.I.)
και το αντίστοιχο διάγραμμα είναι:
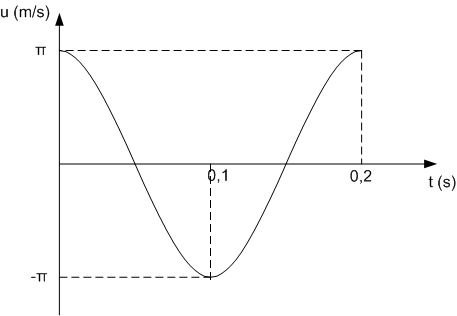
δ.




Το διάγραμμα επιτάχυνσης-απομάκρυνσης είναι:
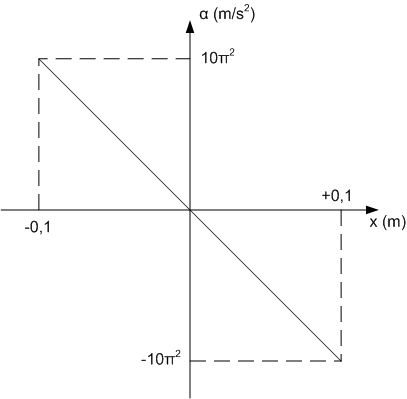
Από το διάγραμμα προκύπτει ότι:
 και
και 
α.
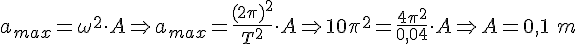
β.


γ.
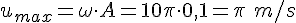
Άρα η εξίσωση της ταχύτητας είναι:

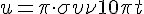 (S.I.)
(S.I.)και το αντίστοιχο διάγραμμα είναι:

δ.





Το διάγραμμα επιτάχυνσης-απομάκρυνσης είναι:


