6.3 - Η συνάρτηση f(x) = αx + β

Γωνία ευθείας με τον x΄x Δώστε μια ευθεία (ε): f(x) = y = αx + β , και βρείτε την γωνία ω που σχηματίζει η ευθεία (ε) με τον x΄x. Eξετάστε πότε η γωνία ω είναι: α)Οξεία β)Ορθή γ)Αμβλεία Boηθητικά αρχεία: Τριγωνομετρικοί πίνακες εφαπτόμενης γωνίας Τριγωνομετρικοί πίνακες

Συντελεστής διεύθυνσης ευθείας Δώστε δύο σημεία Α(x₁ , y₁) , Β(x₂ , y₂) του επιπέδου και βρείτε: α)Τον συντελεστή διεύθυνσης της ευθείας ΑΒ β)Την γωνία ω που σχηματίζει η ευθεία ΑΒ με τον x΄x. γ) Την εξίσωση της ευθείας Boηθητικά αρχεία: Τριγωνομετρικοί πίνακες εφαπτόμενης γωνίας Τριγωνομετρικοί πίνακες

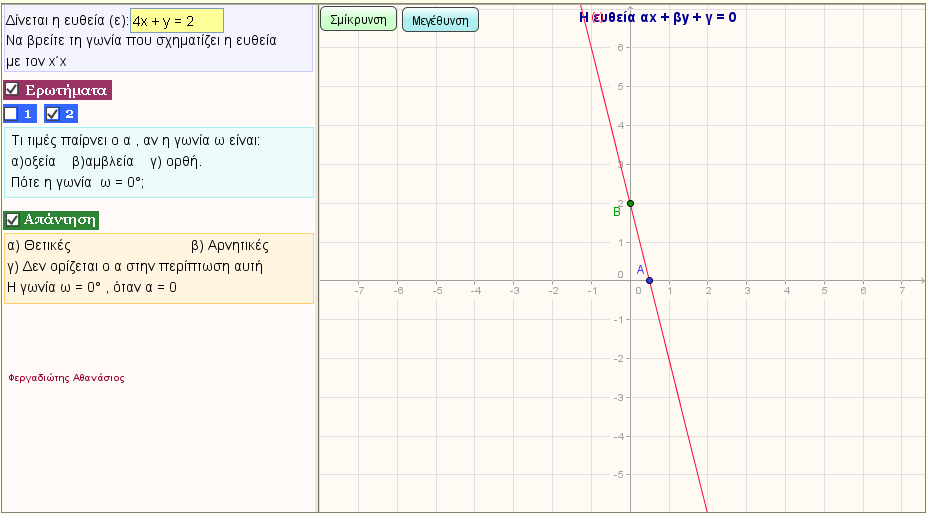
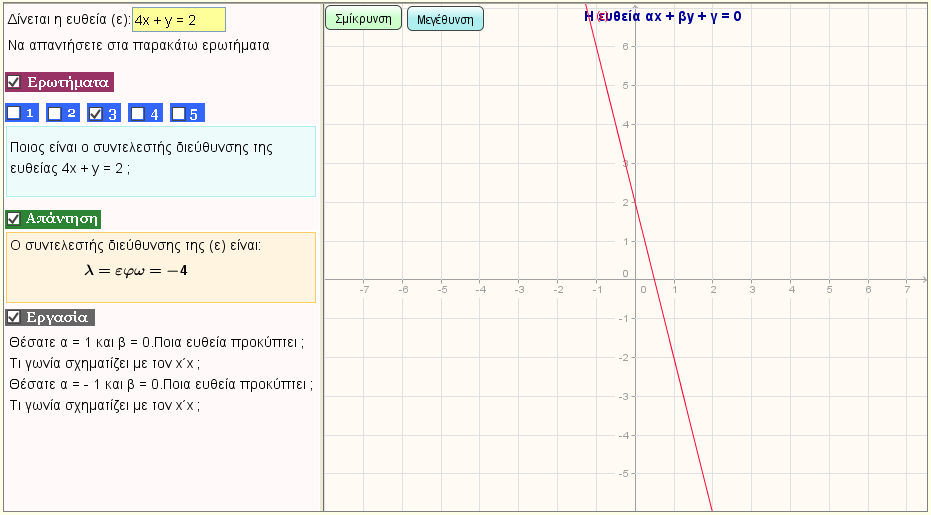
Στοιχεία της ευθείας y = αx + β Δώστε μια ευθεία (ε): f(x) = y = αx + β , και βρείτε α)την γωνία ω που σχηματίζει η ευθεία (ε) με τον x΄x. β)τα σημεία τομής της με τους άξονες γ)τον συντελεστή διεύθυνσης Boηθητικά αρχεία: Τριγωνομετρικοί πίνακες εφαπτόμενης γωνίας Τριγωνομετρικοί πίνακες

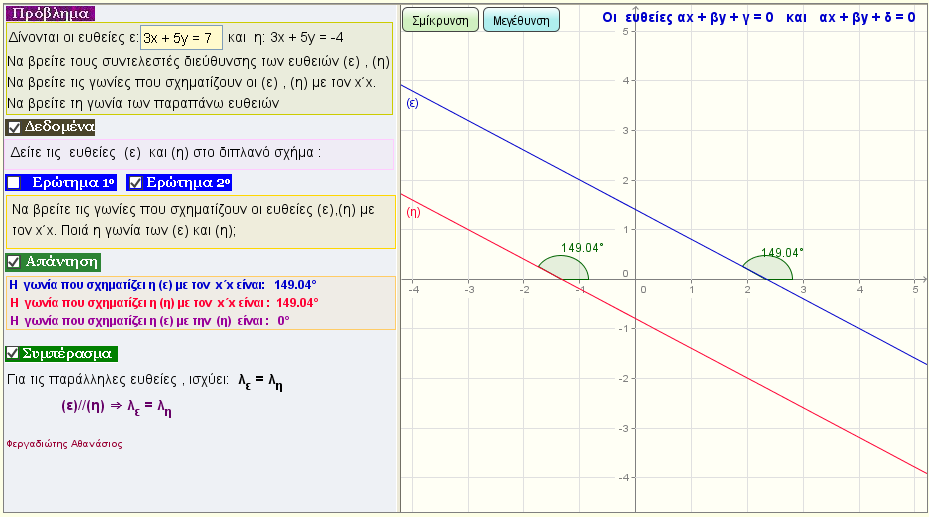
Παράλληλες ευθείες Δώστε τις εξισώσεις δύο ευθειών και εξετάστε ποια σχέση πρέπει να ισχύει για τους συντελεστές διεύθυνσης , για να είναι οι ευθείες παράλληλες Boηθητικά αρχεία: Τριγωνομετρικοί πίνακες εφαπτόμενης γωνίας Τριγωνομετρικοί πίνακες

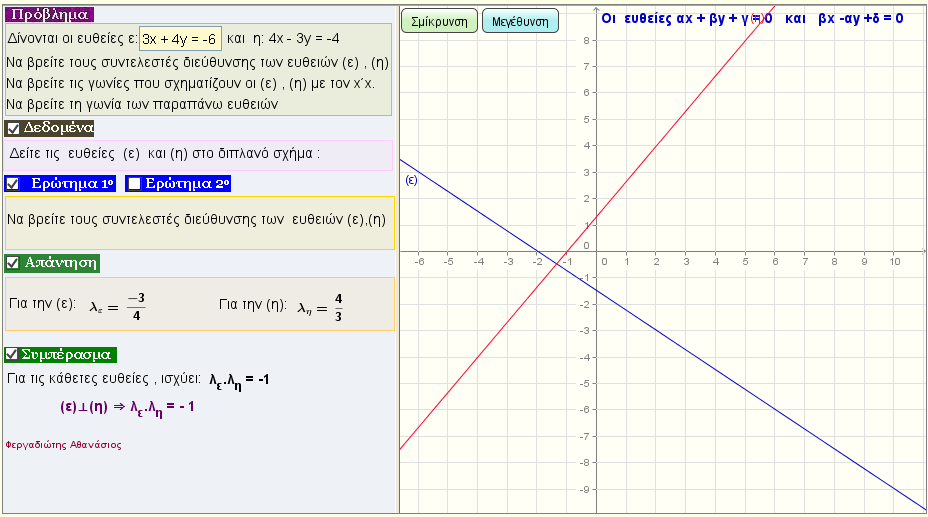
Κάθετες ευθείες Δώστε τις εξισώσεις δύο ευθειών και εξετάστε ποια σχέση πρέπει να ισχύει για τους συντελεστές διεύθυνσης , για να είναι οι ευθείες κάθετες Boηθητικά αρχεία: Τριγωνομετρικοί πίνακες εφαπτόμενης γωνίας Τριγωνομετρικοί πίνακες

Σχετική θέση ευθειών στο επίπεδο Δώστε τις εξισώσεις δύο ευθειών κα εξετάστε πότε οι ευθείες α) Τέμνονται β)Είναι παράλληλες γ)Ταυτίζονται

Οι ευθείες y = λx + β Δώστε την ευθεία με εξίσωση y = λx + β , όπου λ είναι δοσμένος αριθμός και β παράμετρος. α) Τι σχηματίζουν οι παραπάνω ευθείες; β) Ποιά είναι η σχετική τους θέση στο επίπεδο;

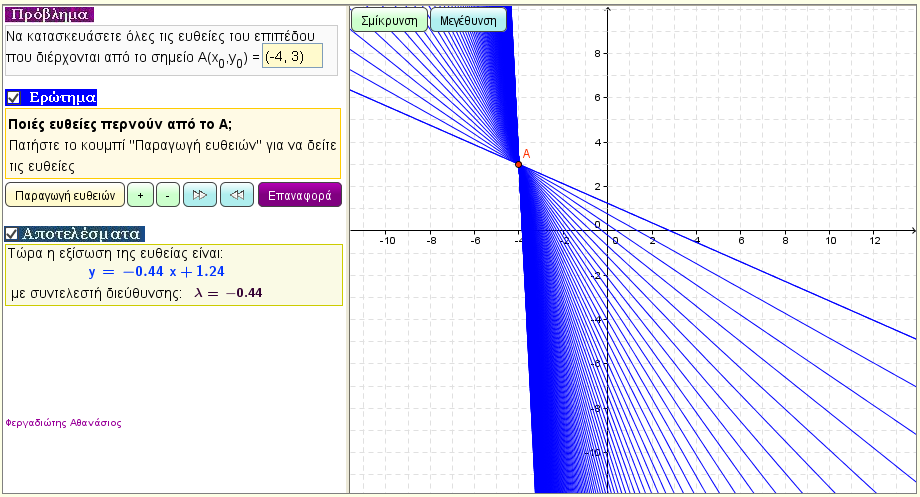
Παραγωγή ευθειών που περνούν από το Α(x₀,y₀) Δώστε το σημείο Α(x₀,y₀) και δείτε τις ευθείες του επιπέδου που περνούν από το σημείο Α. Τι σχηματίζουν οι παραπάνω ευθείες;

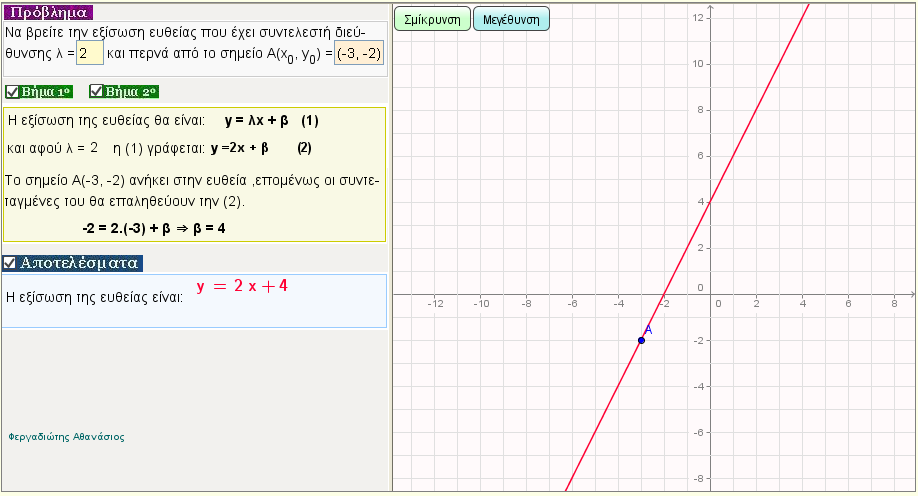
Εξίσωση ευθείας με γνωστό συντελεστή διεύθυνσης λ , που περνά από το σημείο Α(x₀,y₀) Δώστε τον συντελεστή διεύθυνσης της ευθείας και ένα σημείο Α(x₀,y₀) από όπου περνά και βρείτε την εξίσωσή της

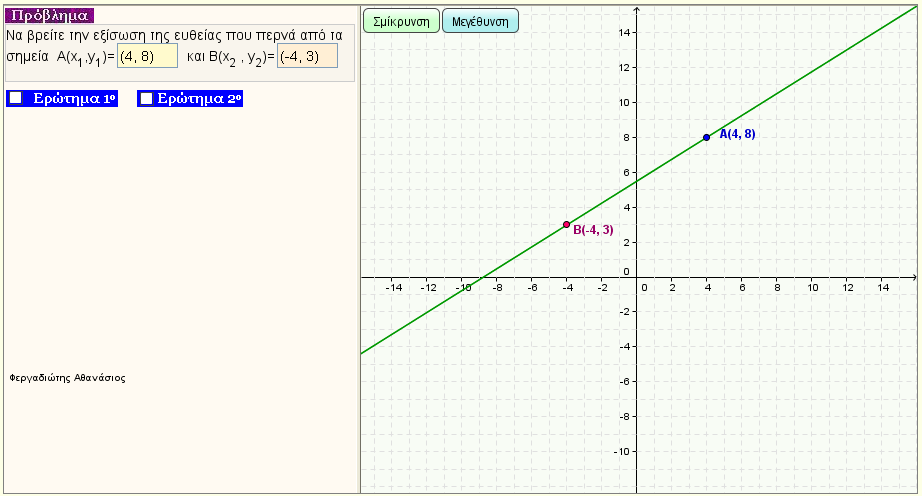
Εξίσωση ευθείας που περνά από τα σημεία Α(x₁,y₁) και Β(x₂,y₂) Δώστε δύο σημεία Α και Β και βρείτε την εξίσωσή της ευθείας ΑΒ

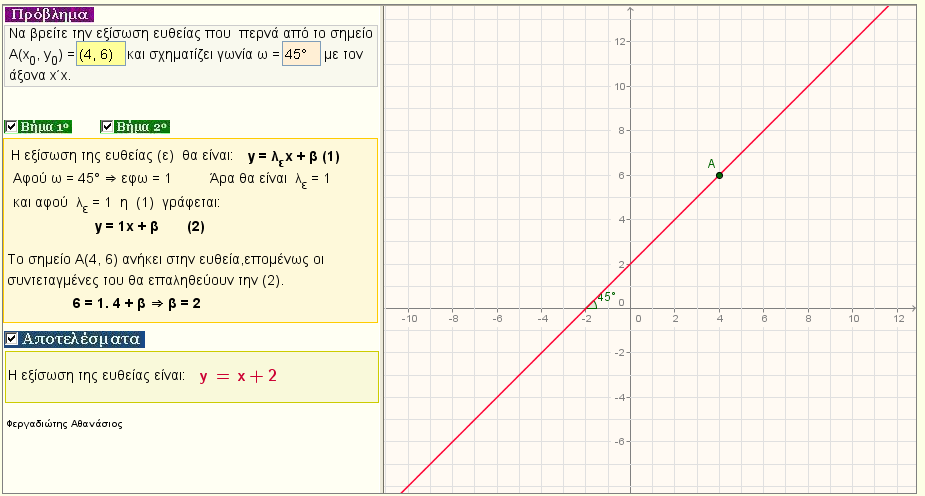
Εξίσωση ευθείας που περνά από το σημείο Α(x₀,y₀) και σχηματίζει γωνία ω με τον x'x Δώστε την γωνία ω = μ⁰ που σχηματίζει η ευθεία με τον x'x και ένα σημείο Α(x₀,y₀) από όπου περνά και βρείτε την εξίσωσή της

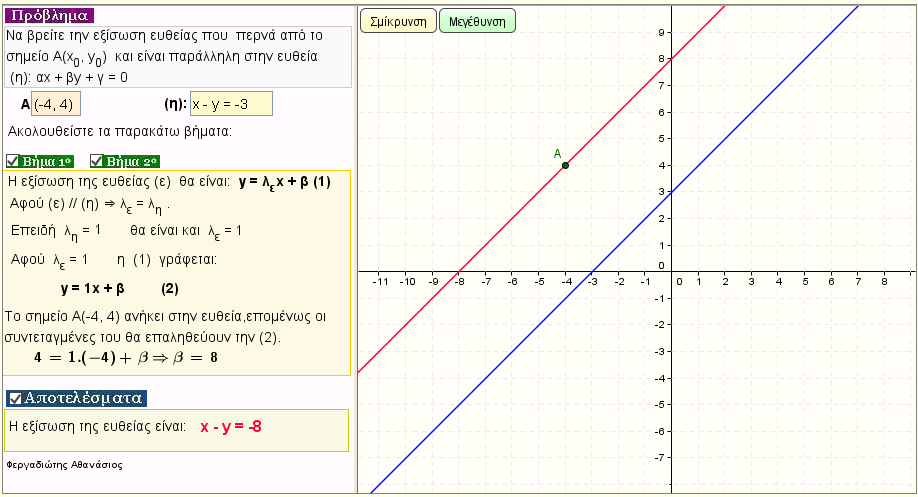
Εξίσωση ευθείας που περνά από το Α(x₀,y₀) και είναι παράλληλη σε δοσμένη ευθεία (η): αx + βy + γ = 0 Βρείτε την εξίσωση της ευθείας που περνά από ένα δοσμένο σημείο Α(x₀,y₀) και είναι παράλληλη σε δοσμένη ευθεία (η) : x+ βy + γ = 0

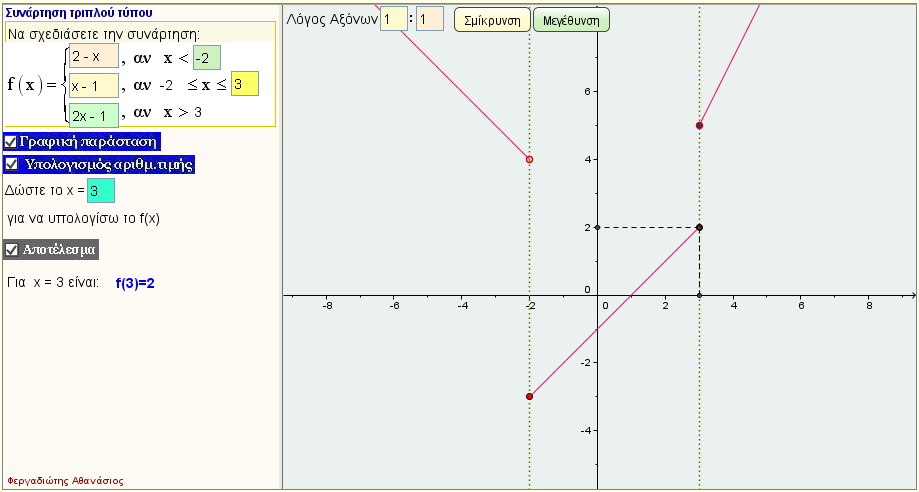
Γράφημα συνάρτησης τριπλού τύπου Δώστε μια συνάρτηση f με τριπλό τύπο , δείτε το γράφημά της και υπολογίστε μερικές αριθμητικές τιμές της

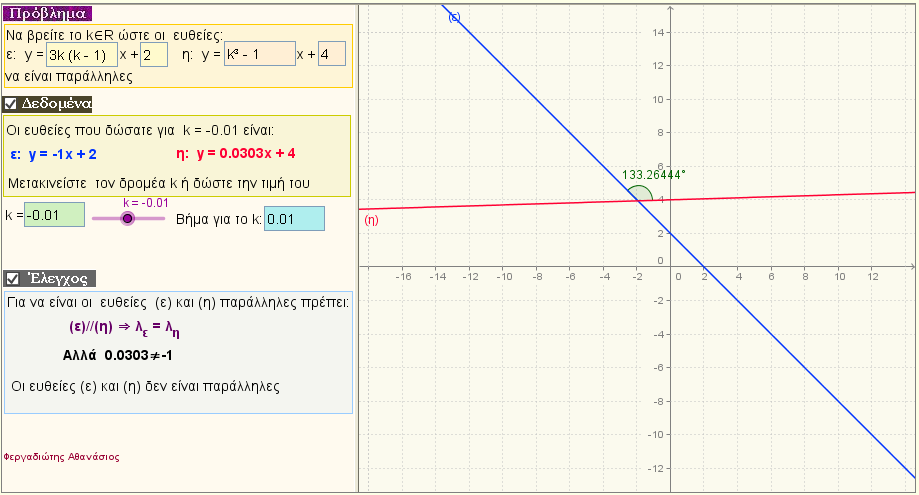
Πρόβλημα 1 Δίνονται οι ευθείες (ε): f(x) = g(k)x + α (η): h(x) =r(k)x + β Βρείτε τον πραγματικό αριθμό k , για να είναι οι ευθείες παράλληλες

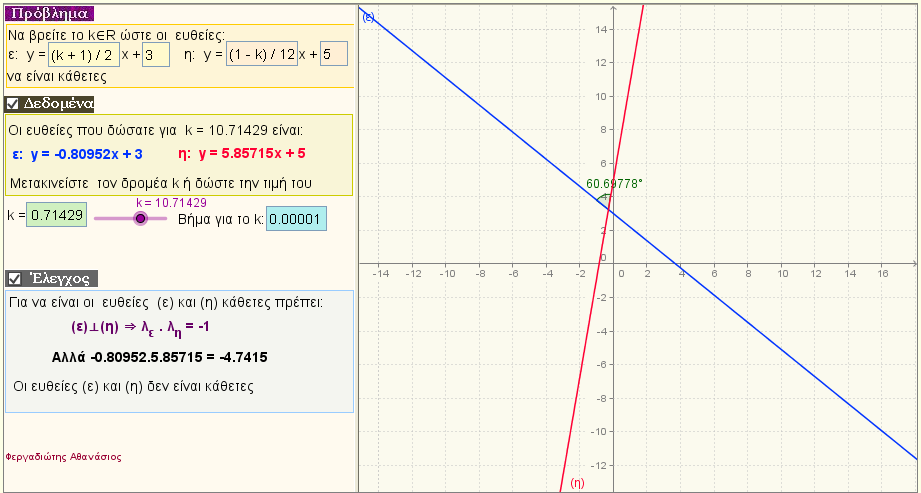
Πρόβλημα 2 Δίνονται οι ευθείες (ε): f(x) = g(k)x + α (η): h(x) =r(k)x + β Βρείτε τον πραγματικό αριθμό k , για να είναι οι ευθείες κάθετες

Πρόβλημα 3 Να βρείτε την εξίσωση της ευθείας που παριστάνει τη σχέση μεταξύ της θερμοκρασίας σε βαθμούς Celsius (C^ο) και σε βαθμούς Fahrenheit (F). Γνωρίζουμε ότι το νερό παγώνει στους 0^οC ή 32^οF και βράζει σε 100^οC ή 212^οF

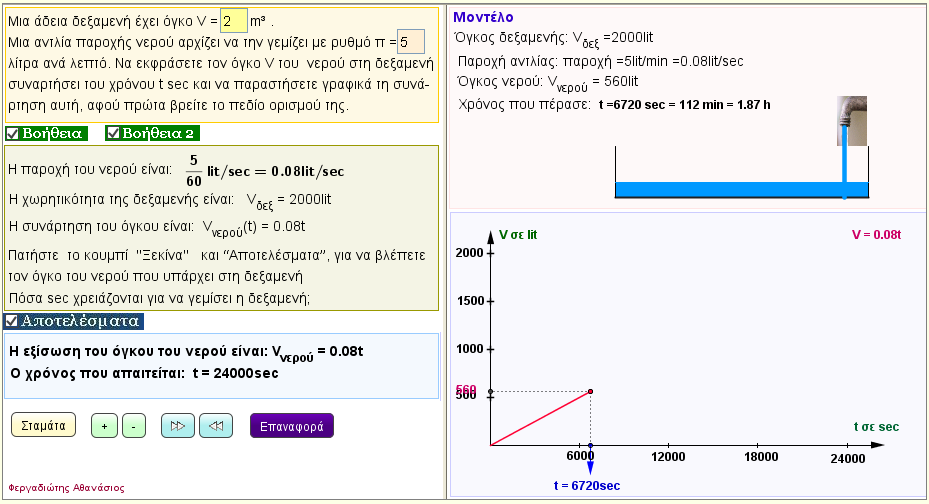
Πρόβλημα 4 Μια άδεια δεξαμενή έχει όγκο V = α m³. Mια αντλία παροχής νερού αρχίζει να την γεμίζει με ρυθμό β λίτρα ανά λεπτό. Να εκφράσετε τον όγκο V του νερού στη δεξαμενή συναρτήσει του χρόνου t sec και να παραστήσετε γραφικά τη συνάρτηση αυτή , αφού πρώτα βρείτε το πεδίο ορισμού της.

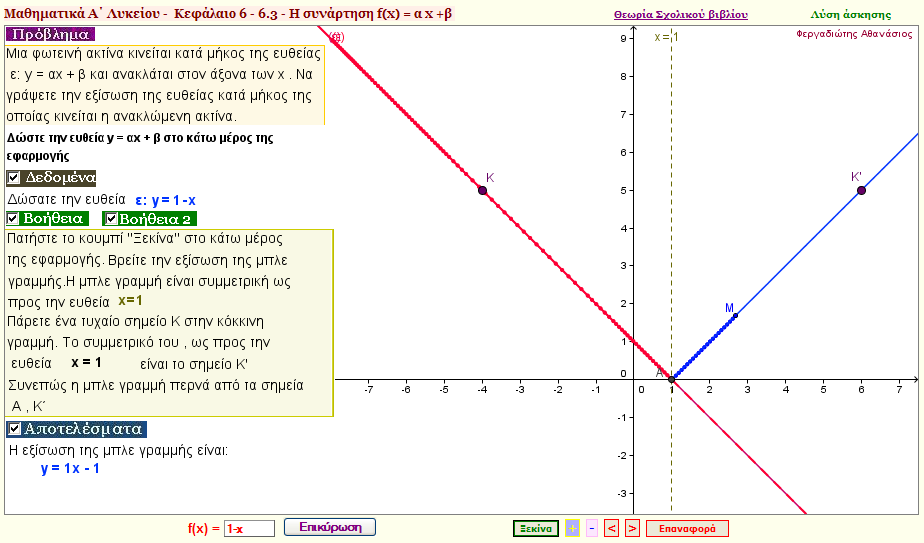
Πρόβλημα 5 Μια φωτεινή ακτίνα κινείται κατά μήκος της ευθείας y = kx+ λ και ανακλάται στον άξονα x΄x .Nα γράψετε την εξίσωση της ευθείας κατά μήκος της οποίας κινείται η ανακλώμενη ακτίνα.

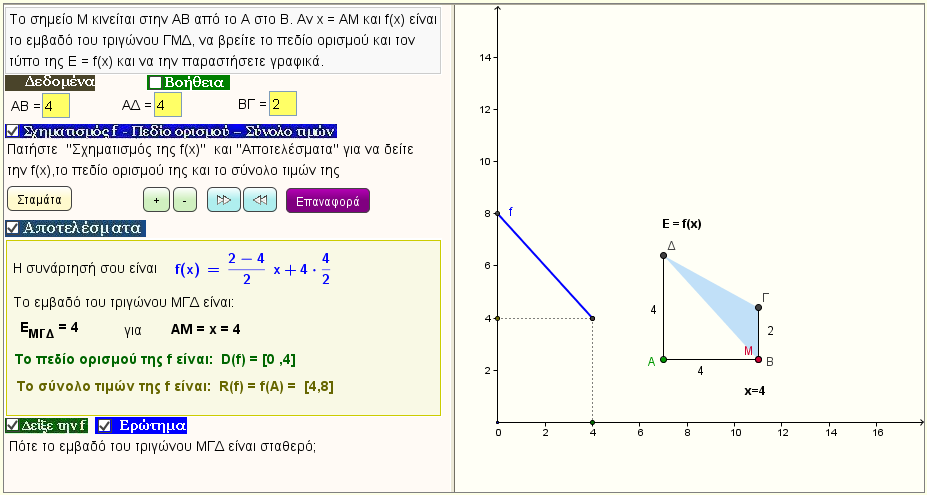
Πρόβλημα 6 Στο διπλανό σχήμα το σημείο Μ διαγράφει το ευθύγραμμο τμήμα ΑΒ από το Α προς το Β. Συμβολίζουμε με x το μήκος της διαδρομής ΑΜ του σημείου Μ και με f (x) το εμβαδόν του τριγώνου Μ Γ Δ. Να βρείτε το πεδίο ορισμού και τον τύπο της συνάρτησης E=f (x) και στη συνέχεια να την παραστήσετε γραφικά.

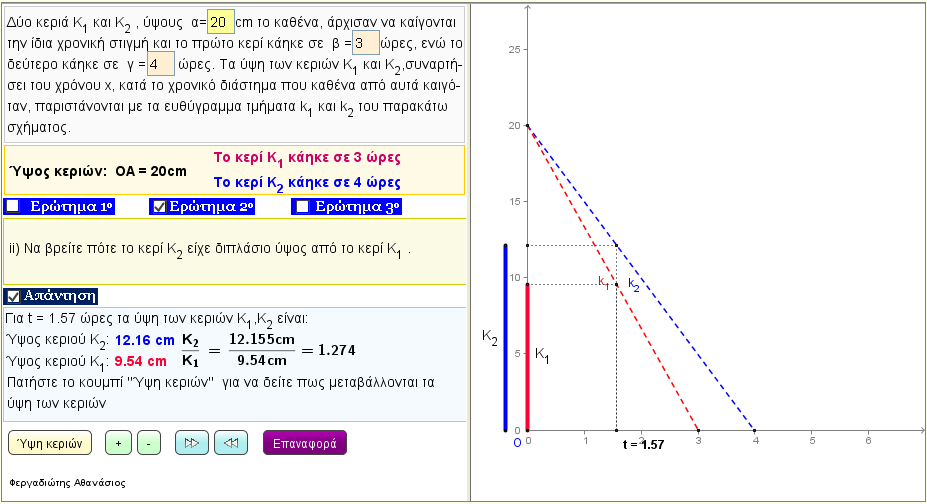
Πρόβλημα 7 Δύο κεριά Κ₁ και Κ₂ , ύψους 20 cm το καθένα, άρχισαν να καίγονται την ίδια χρονική στιγμή και το πρώτο κερί κάηκε σε 3 ώρες, ενώ το δεύτερο κάηκε σε 4 ώρες. Τα ύψη των κεριών Κ₁ και Κ₂ , συναρτήσει του χρόνου x, κατά το χρονικό διάστημα που καθένα από αυτά καιγόταν, παριστάνονται με τα ευθύγραμμα τμήματα k₁ και k₂ του παρακάτω σχήματος. i) Να βρείτε τις συναρτήσεις h₁(x) και h₂(x) που εκφράζουν, συναρτήσει του χρόνου x τα ύψη των κεριών K₁ και Κ₂ αντιστοίχως. ii) Να βρείτε πότε το κερί Κ₂ είχε διπλάσιο ύψος από το κερί Κ₁ . iii) Να λύσετε το ίδιο πρόβλημα και στη γενική περίπτωση που το αρχικό ύψος των κεριών ήταν ίσο με α. Τι παρατηρείτε;