4.3 - Ανισώσεις Γινόμενο και Ανισώσεις Πηλίκο



Ανισώσεις Γινόμενο και ανισώσεις Πηλίκο

Γ. ΕΦΑΡΜΟΓΕΣ
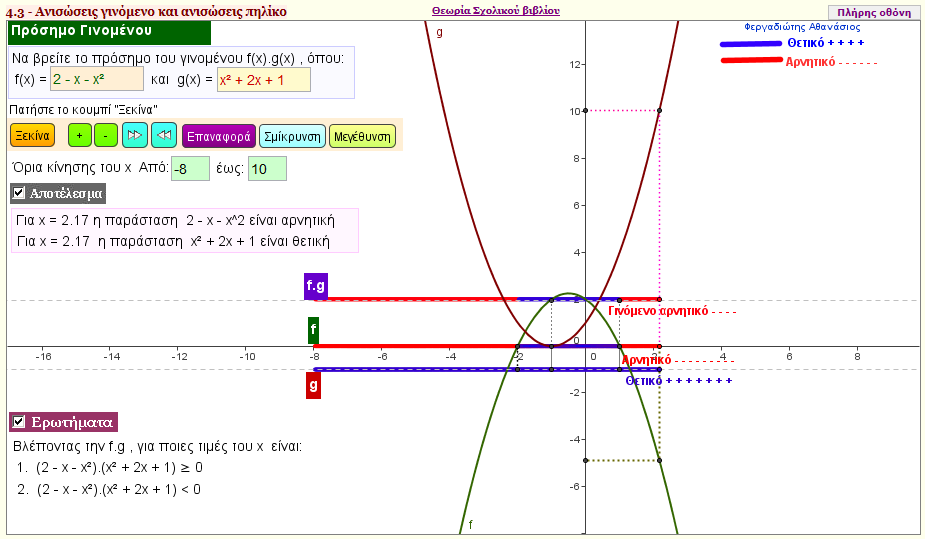
Το πρόσημο του γινομένου Δώστε δύο τριώνυμα f(x) = αx² + βx + γ και g(x) = κx²+ λx+ μ και βρείτε το πρόσημο του γινομένου f(x).g(x) για τις διάφορες πραγματικές τιμές των α , β , γ , κ , λ, μ.

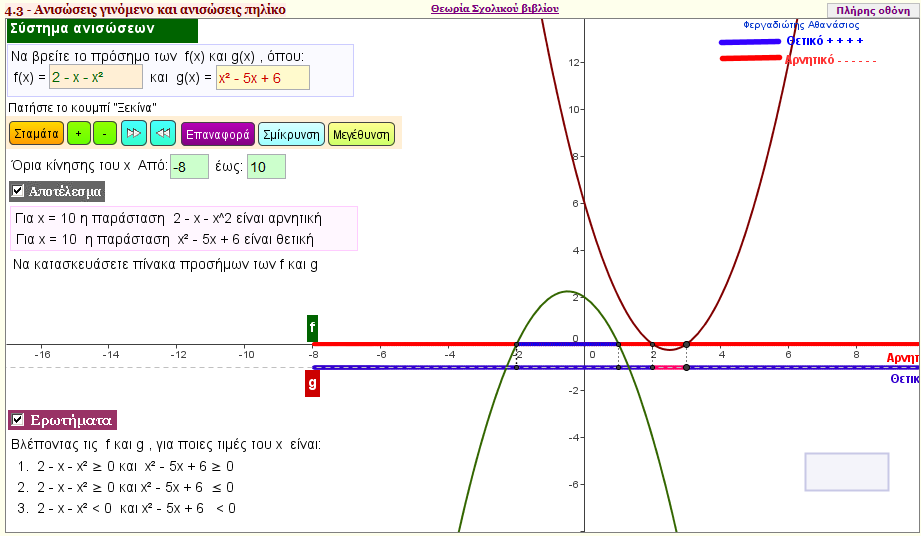
Σύστημα ανισώσεων Δώστε δύο τριώνυμα f(x) = αx² + βx + γ και g(x) = κx²+ λx+ μ και λύσετε το σύστημα π.χ f(x)>0 και g(x) < 0 για τις διάφορες πραγματικές τιμές των α , β , γ , κ , λ, μ.

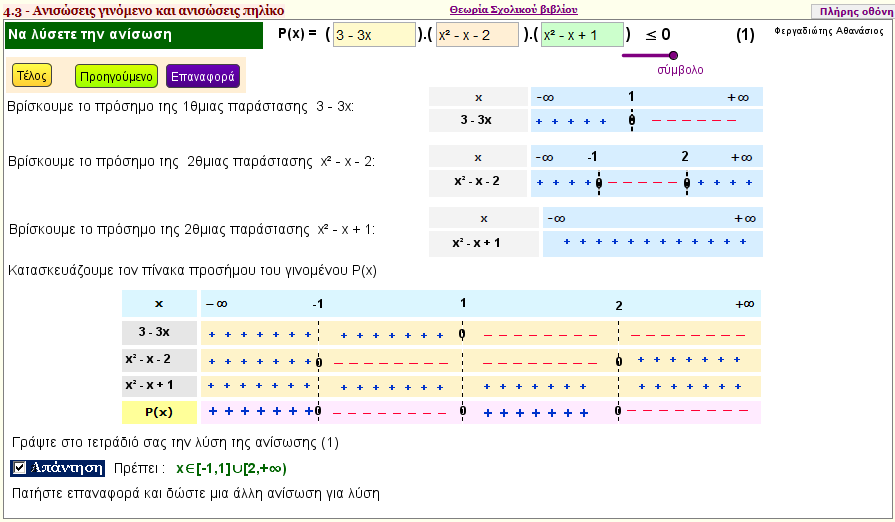
Λύση ανίσωσης (γινόμενο) Δώστε μία ανίσωση της μορφής f(x).g(x).h(x) >0 και βρείτε σε ποια υποδιαστήματα του R αληθεύει. Η εφαρμογή συντάσσει συγκεντρωτικό πίνακα του προσήμου των f , g , h καθώς και του γινομένου P(x) = f(x)g(x)h(x) Σημείωση Αν θέλετε να λύσετε ανίσωση της μορφής f(x)g(x) > 0 , θέστε h(x) = 1 Τα πολυώνυμα f(x) , g(x) , h(x) είναι το πολύ β΄ βαθμού. Με την βοήθεια της εφαρμογής αυτής να λύσετε τις ασκήσεις 1,2,3,4,5,6 α΄ ομάδας της σελίδας 117 του σχολικού σας βιβλίου

Λύση ανίσωσης (πηλίκο) Δώστε μία ανίσωση της μορφής f(x)/g(x) >0 και βρείτε σε ποια υποδιαστήματα του R αληθεύει. Με την βοήθεια της εφαρμογής αυτής να λύσετε τις ασκήσεις 7,8 της α΄ ομάδας καθώς και τις 1,2,3 της β΄ ομάδας των σελίδων 117-118 του σχολικού σας βιβλίου

Άσκηση 5 Β΄ Ομάδας Μία εταιρεία παράγει ηλεκτρικούς λαμπτήρες. Για ένα συγκεκριμένο τύπο λαμπτήρων το τμήμα έρευνας αγοράς της εταιρείας εκτιμά ότι αν η τιμή πώλησης των λαμπτήρων είναι x ευρώ ανά λαμπτήρα, τότε το εβδομαδιαίο κόστος Κ και τα αντίστοιχα έσοδα Ε (σε χιλιάδες ευρώ) δίνονται από τους τύπους Κ = 7 - x και Ε = 5x - x² . Να βρείτε τις τιμές πώλησης των λαμπτήρων για τις οποίες η εταιρεία έχει κέρδος.

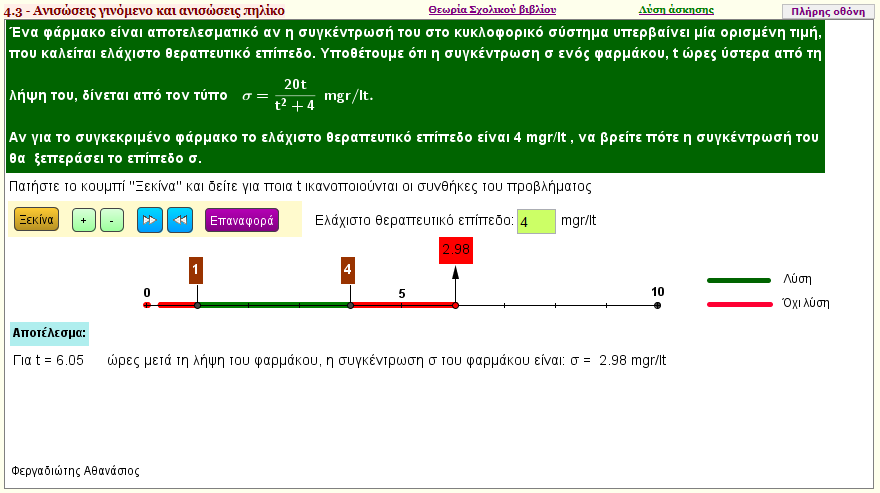
Άσκηση 6 Β΄ Ομάδας Ένα φάρμακο είναι αποτελεσματικό αν η συγκέντρωσή του στο κυκλοφορικό σύστημα υπερβαίνει μία ορισμένη τιμή,που καλείται ελάχιστο θεραπευτικό επίπεδο. Υποθέτουμε ότι η συγκέντρωση σ ενός φαρμάκου, t ώρες ύστερα από τη λήψη του, δίνεται από τον τύπο σ = 20t/(t²+4) mgr/lt. Αν για το συγκεκριμένο φάρμακο το ελάχιστο θεραπευτικό επίπεδο είναι 4mgr/lt , να βρείτε πότε η συγκέντρωσή του θα ξεπεράσει το επίπεδο σ.