2.4 - Ρίζες πραγματικών αριθμών

Ρίζες πραγματικών αριθμών

Α. Θεωρία - Μεθοδολογία			Β. Ασκήσεις
Βασική θεωρία στις ρίζες των πραγματικών αριθμών 1 . Θεωρία			Πακέτα λυμένων ασκήσεων , για εμπέδωση της θεωρίας 1 . Ασκήσεις Αντιστοίχισης

Γ. VIDEO
Αλγόριθμος εύρεσης τετραγωνικής ρίζας - 1
Αλγόριθμος εύρεσης τετραγωνικής ρίζας - 2

Γ. Εφαρμογές
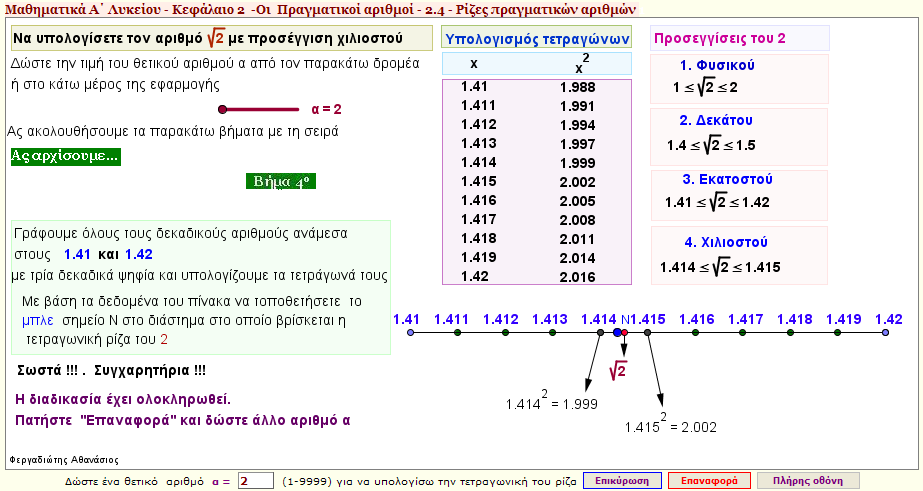
Προσέγγιση τετραγωνικής ρίζας θετικού αριθμού - Εργασία 1 Δώστε ένα αριθμό από 1 -9999 και προσπαθείστε ακολουθώντας τα βήματα της εφαρμογής να υπολογίσετε την τετραγωνική ρίζα του αριθμού με έλλειψη και υπεροχή

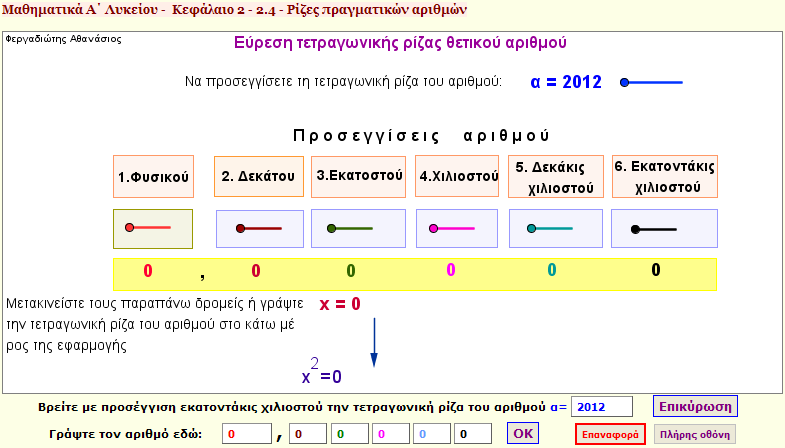
Εύρεσης τετραγωνικής ρίζας - Εργασία 2 Δώστε ένα αριθμό α και προσπαθείστε μετακινώντας τους δρομείς ή γράφοντας κατάλληλα ψηφία στο κάτω μέρος της εφαρμογής , να υπολογίσετε την τετραγωνική ρίζα του α με έλλειψη και υπεροχή.

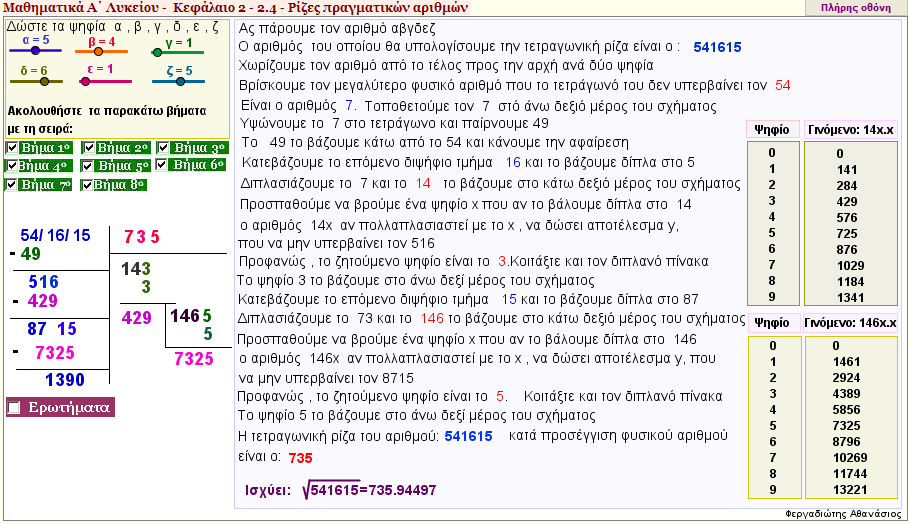
Αλγόριθμος εύρεσης τετραγωνικής ρίζας Στην εφαρμογή αυτή, αναπτύσσεται ένας αλγόριθμος εύρεσης της τετραγωνικής ρίζας ενός πραγματικού αριθμού. Ακολουθείστε ένα προς ένα τα βήματα της εφαρμογής

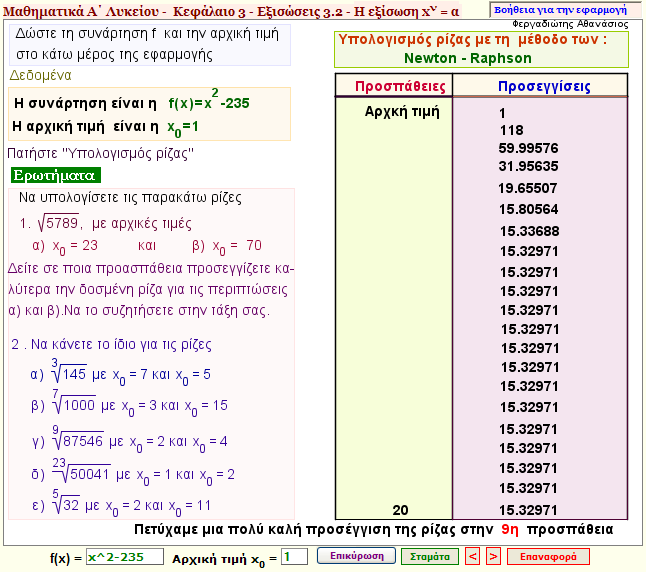
Εύρεση τετραγωνικής ρίζας φυσικού αριθμού - Μέθοδος Newton-Raphson Στην εφαρμογή αυτή, αναπτύσσεται ένας άλλος αλγόριθμος εύρεσης της τετραγωνικής ρίζας ενός φυσικού αριθμού, σύμφωνα με την μέθοδο Newton - Raphson

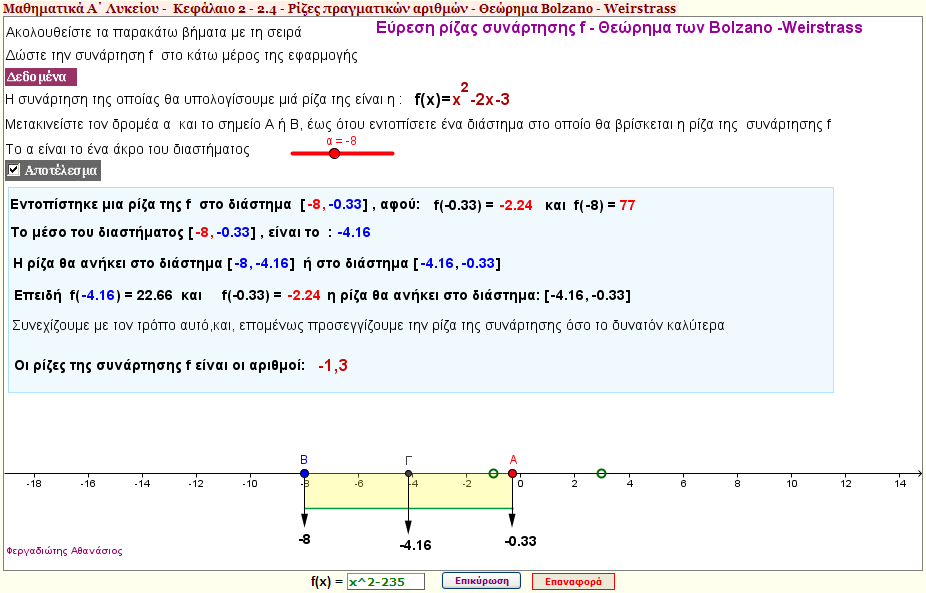
Θεώρημα του Βοlzano Στην εφαρμογή αυτή, αναπτύσσεται ένας άλλος αλγόριθμος εύρεσης της τετραγωνικής ρίζας ενός φυσικού αριθμού, σύμφωνα με την μέθοδο Bolzano

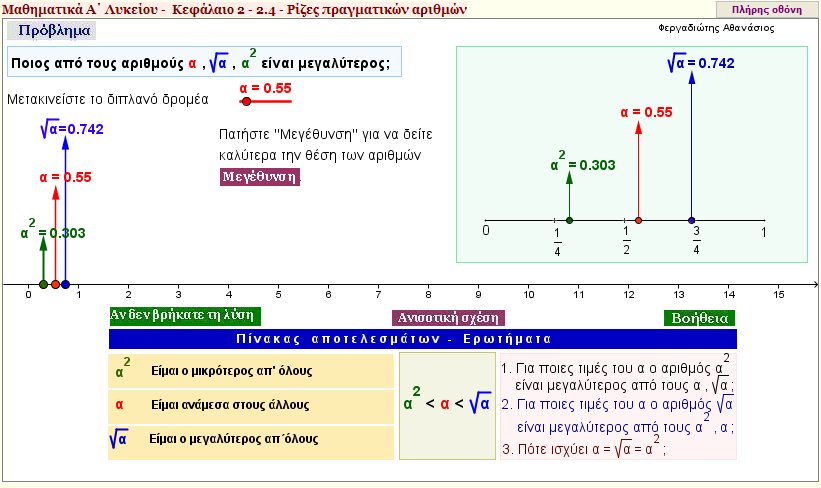
Πρόβλημα 1 Δίνονται οι αριθμοί α , α² και $ \sqrt{α} $ Ποιος από τους παραπάνω αριθμούς είναι ο μεγαλύτερος; Τι συμβαίνει όταν α) α >1; β) α = 1; γ) α < 1;

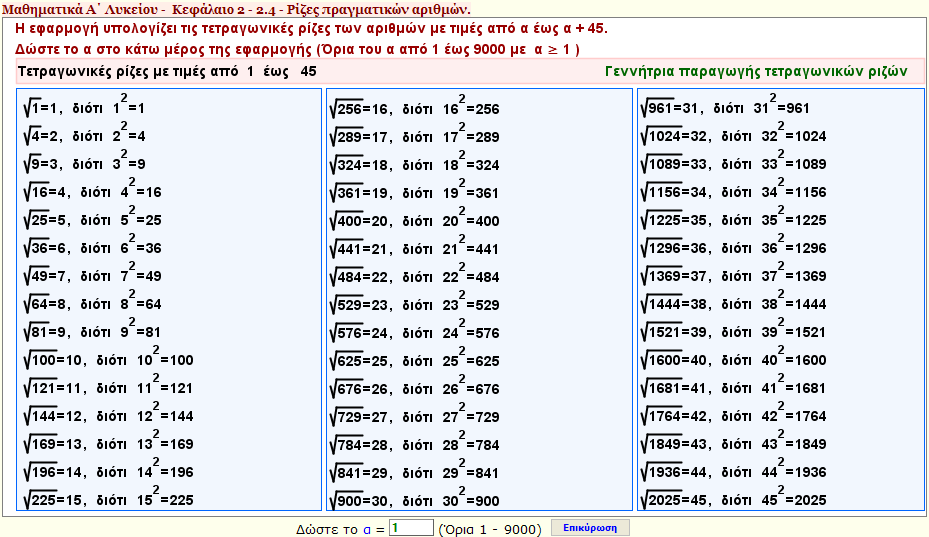
Γεννήτρια παραγωγής τετραγωνικών ριζών Η εφαρμογή υπολογίζει τις τετραγωνικές ρίζες αριθμών με τιμές από α έως α +45 Δώστε τη τιμή του α και θα υπολογιστούν όλες οι τετραγωνικές ρίζες των αριθμών που οι τιμές τους είναι από α έως α + 45

EΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ 2 ΚΕΦΑΛΑΙΟΥ (ΤΕΣΤ)
Το τεστ περιέχει 33 ερωτήσεις και διαπραγματεύεται τις παραγράφους 2.1 , 2.2 , 2.3 και 2.4 του 2ου κεφαλαίου των πραγματικών αριθμών.Προσπαθείστε να πετύχετε βαθμολογία τουλάχιστον 75% (15)			Τ ε σ τ - Ε ρ ω τ ή σ ε ι ς κ α τ α ν ό η σ η ς