| 3.2 Η Παραβολή |
|
|
|
| Α. Θεωρία |
|
|
Β. Ασκήσεις |
| Θεωρία σχολικού βιβλίου |
|
|
Aσκήσεις ανάπτυξης |
| Παραμετρικές εξισώσεις |
|
|
Aσκήσεις αντιστοίχισης |
| Γενική εξίσωση της παραβολής |
|
|
Aσκήσεις πολλαπλής επιλογής |
| |
|
|
Aσκήσεις Σωστό - Λάθος |
| |
|
|
Aσκήσεις συμπλήρωσης κενού |
| |
|
|
Aσκήσεις διάταξης |
| |
|
|
|
| |
|
|
Aσκήσεις σχολικού βιβλίου |
| Γ. Εφαρμογές |
|
|
|
Κατασκευή της παραβολής 1
Βρείτε τον γεωμετρικό τόπο των σημείων του επιπέδου, που ισαπέχουν από μια ευθεία (ε) και από ένα σταθερό σημείο Μ. |
|
|
 |
| |
|
|
|
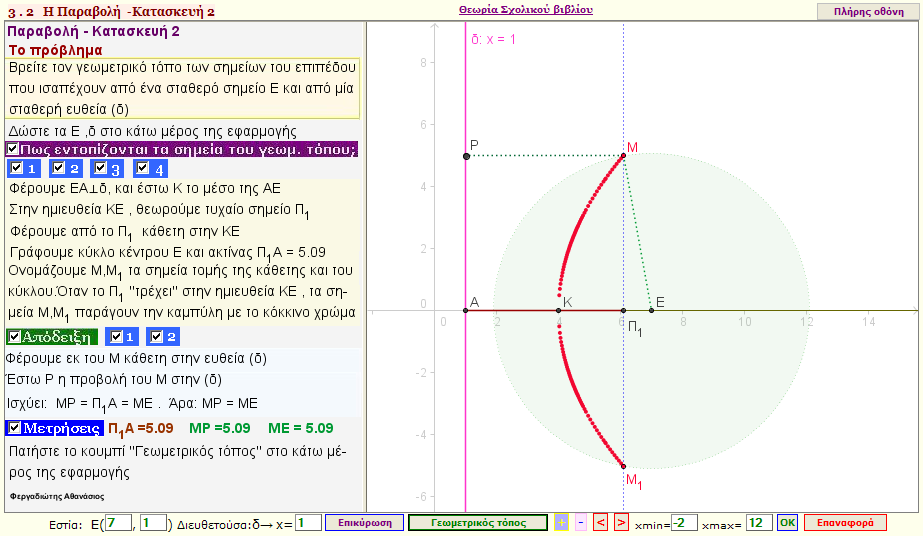
Κατασκευή της παραβολής 2
Βρείτε τον γεωμετρικό τόπο των σημείων του επιπέδου, που ισαπέχουν από μια σταθερή ευθεία (δ) και από ένα σταθερό σημείο Ε. |
|
|
 |
| |
|
|
|
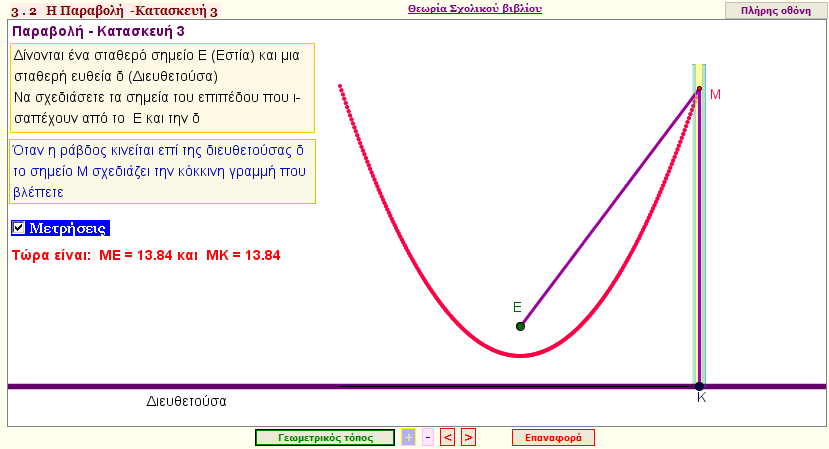
Κατασκευή της παραβολής 3
Βρείτε τον γεωμετρικό τόπο των σημείων του επιπέδου, που ισαπέχουν από μια σταθερή ευθεία (δ) και από ένα σταθερό σημείο Ε. |
|
|
 |
| |
|
|
|
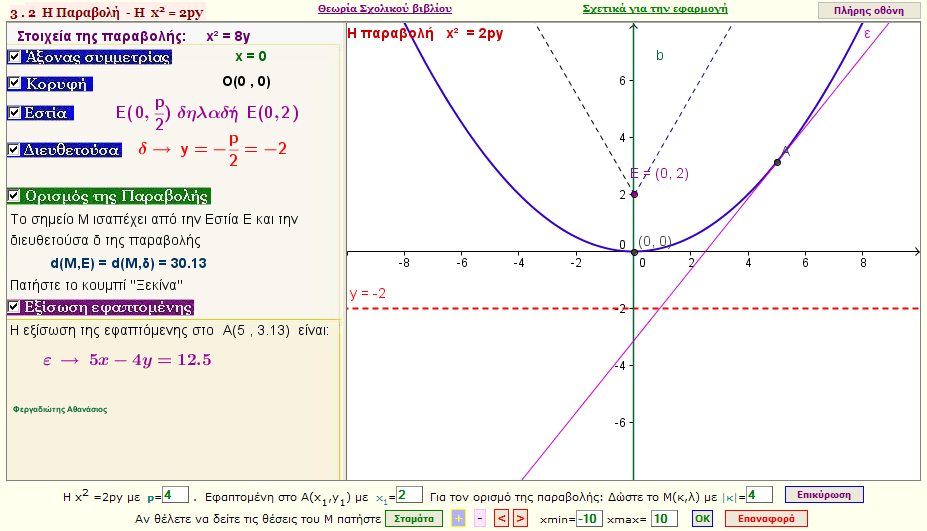
Στοιχεία της παραβολής 1
Μελέτη παραβολής οποιασδήποτε μορφής
Δώστε την εξίσωση οποιασδήποτε παραβολής για να μελετηθούν τα παρακάτω:
Άξονας συμμετρίας , Κορυφή , Εστία ,Διευθετούσα , Εξίσωση εφαπτόμενης σε σημείο της |
|
|
 |
| |
|
|
|
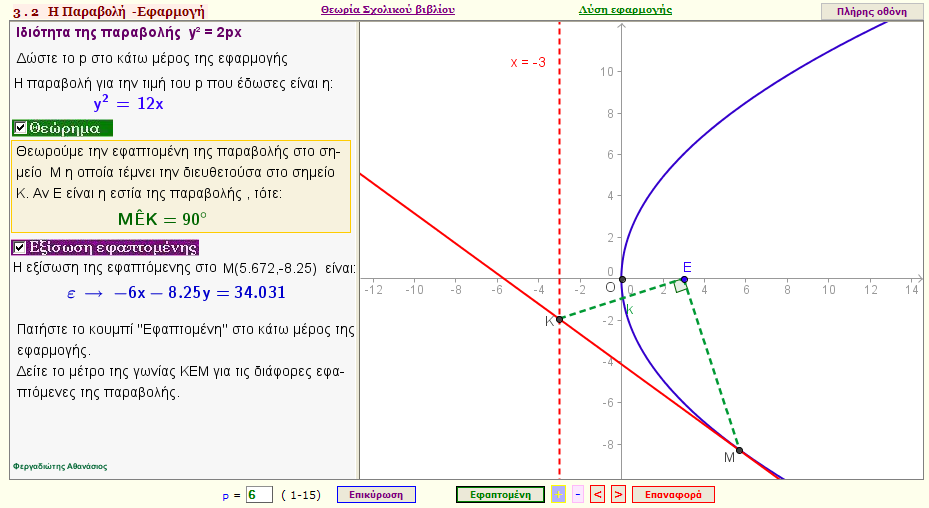
Eφαρμογή - Ιδιότητα της παραβολής
Θεωρούμε την εφαπτομένη της παραβολής στο σημείο Μ, η οποία τέμνει την διευθετούσα στο σημείο Κ.
Αν Ε είναι η εστία της παραβολής , τότε η γωνία ΜΕΚ = 90ο |
|
|
 |
| |
|
|
|
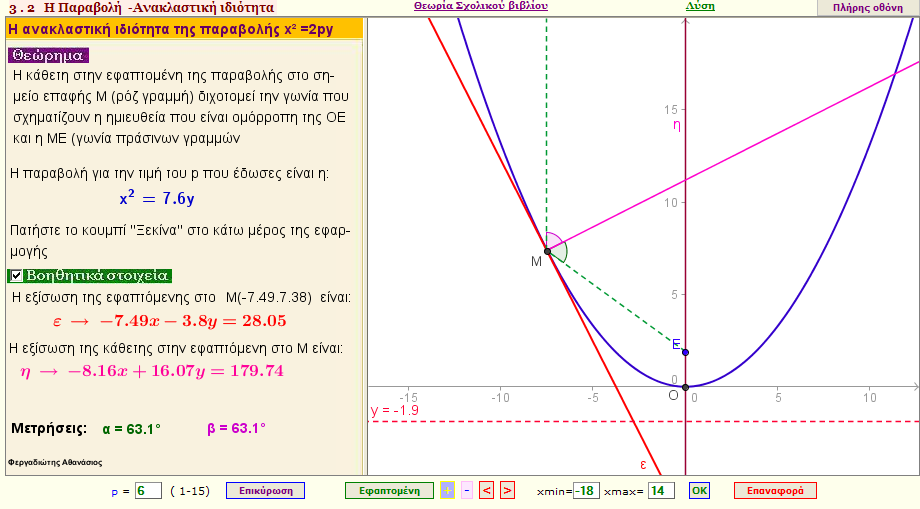
Ανακλαστική ιδιότητα της παραβολής - Θεωρητικό μέρος
Η κάθετη στην εφαπτομένη της παραβολής στο σημείο επαφής Μ , διχοτομεί την γωνία που σχηματίζουν η ημιευθεία που είναι ομόρροπη της ΟΕ και η ΜΕ , όπου Ε είναι η εστία της παραβολής.
|
|
|
 |
| |
|
|
|
|
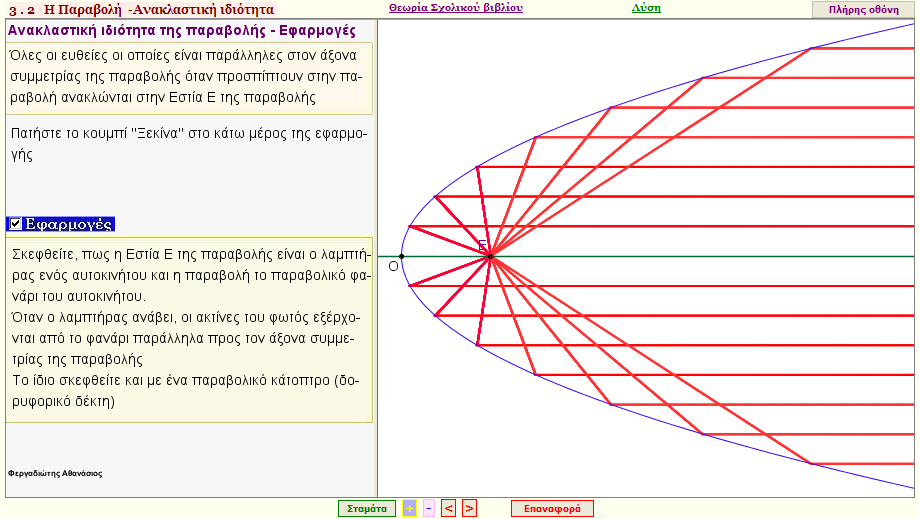
Ανακλαστική ιδιότητα της παραβολής - Εφαρμογή
Όλες οι ευθείες , που είναι παράλληλες στον άξονα συμμετρίας της παραβολής , όταν προσπίπτουν στην παραβολή , ανακλώνται στην Εστία της παραβολής.
|
|
|
 |
| |
|
|
|
|
Ανακλαστική ιδιότητα της παραβολής - Προσομοίωση
Προσομοίωση λήψης δορυφορικών σημάτων από ραδιοτηλεσκόπιο.
Μια εφαρμογή , για την κατανόηση της ανακλαστικής ιδιότητας της παραβολής.
Δώστε την γωνία κλίσης του ραδιοτηλεσκοπίου , το πλήθος των ηλεκτρομαγνητικών κυμάτων που θα πέφτουν στο παραβολικό κάτοπτρο και μετά πατήστε το κουμπί ΄΄Ξεκίνα΄΄.
|
|
|
 |
| |
|
|
|
|
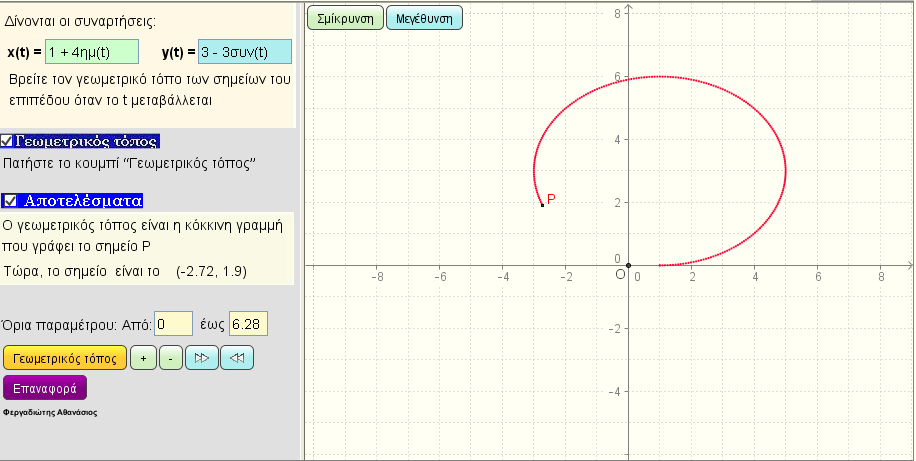
Παραμετρικές εξισώσεις καμπύλης 1
Δώστε τις παραμετρικές εξισώσεις x(t) = ... ,y(t) = .... , ως συνάρτηση του t , και δείτε τον γεωμετρικό τόπο των σημείων Μ(x(t),y(t)) στο επίπεδο.
|
|
|
 |
| |
|
|
|
|
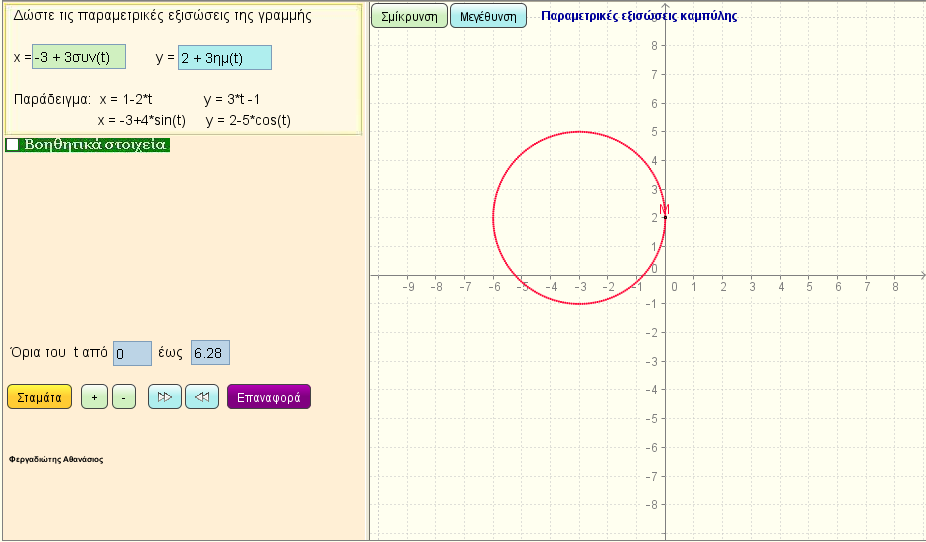
Παραμετρικές εξισώσεις καμπύλης 2
Δώστε τις παραμετρικές εξισώσεις x(t) = ... ,y(t) = .... , ως συνάρτηση του t , και δείτε τον γεωμετρικό τόπο των σημείων Μ(x(t),y(t)) στο επίπεδο.
|
|
|
 |