Α - Κεφάλαιο 1 - 1.2 - Εξισώσεις α΄ βαθμού.

Μέρος Α' - Κεφάλαιο 1
1.2 - Eξισώσεις α΄ βαθμού

Α . Θεωρία			Β . Ασκήσεις - Τεστ
1. Θεωρία του σχολικού βιβλίου			1.Λύσεις ασκήσεων σχολικού βιβλίου και ερωτήσεων κατανόησης


Γ . Εφαρμογές
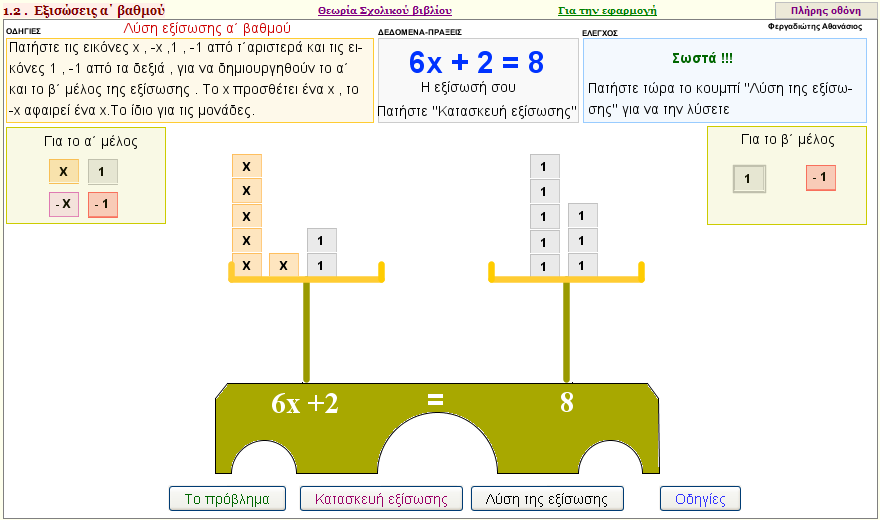
H έννοια της εξίσωσης Πώς λύνεται μια εξίσωση α΄ βαθμού; Λύσετε π.χ την εξίσωση 3x - 2 = 4 Προσομοίωση της εξίσωσης με ζυγαριά που ισορροπεί. Πλήρης πρακτική εξάσκηση για τον μαθητή.

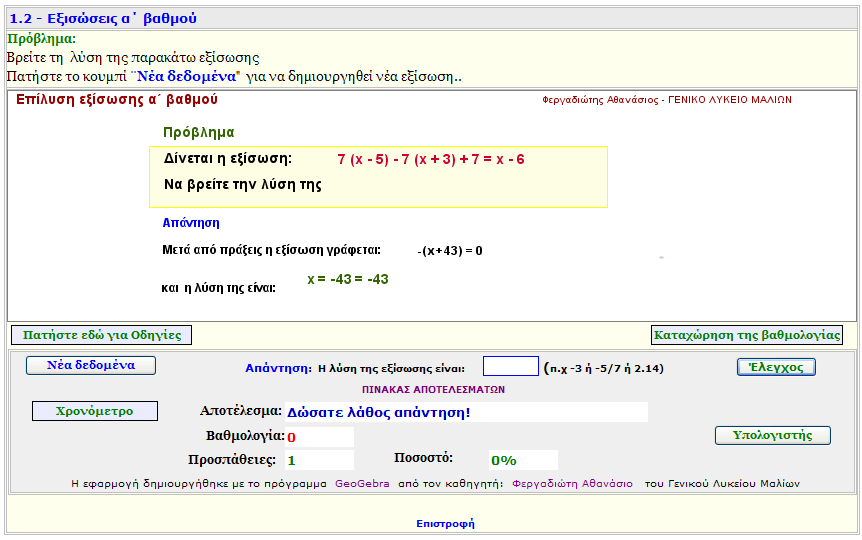
Εφαρμογή 1 - 3 (Tεστ) Βρείτε τη λύση της εξίσωσης π.χ 2(x + 1) + 3(2 - x) = 4(x + 2) Πρακτική εξάσκηση. Απαντήστε σωστά και μαζέψτε , όσους περισσσότερους βαθμούς μπορείτε. Η βαθμολογία σας κατωχυρώνεται μόνο αν είναι μεγαλύτερη από 139 βαθμούς.

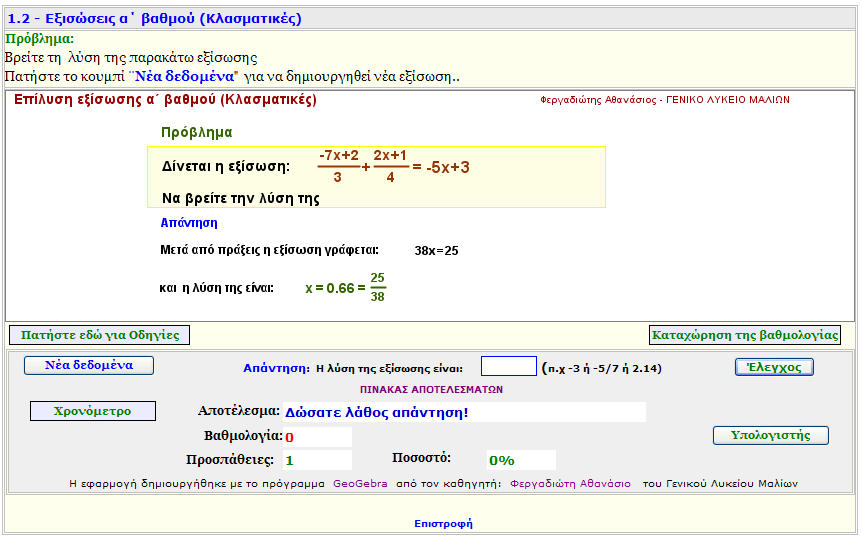
Εφαρμογή 2 - 4 (Τεστ) Βρείτε τη λύση μιας κλασματικής εξίσωσης α΄ βαθμού. Πρακτική εξάσκηση. Απαντήστε σωστά και μαζέψτε , όσους περισσσότερους βαθμούς μπορείτε. Η βαθμολογία σας κατωχυρώνεται μόνο αν είναι μεγαλύτερη από 99 βαθμούς.


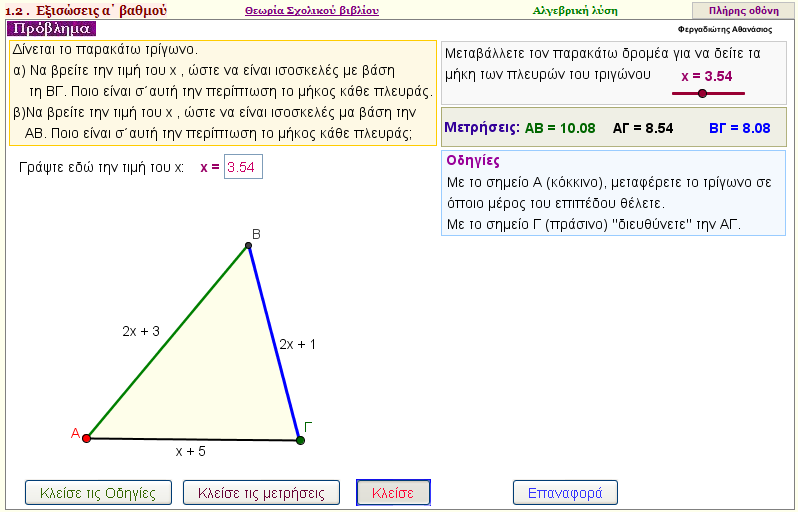
Άσκηση 10 Δίνεται τρίγωνο με πλευρές ΑΒ = 2x + 3 , AΓ = x + 5 , BΓ = 2x + 1 . Να βρεθεί η τιμή του x , ώστε να είναι ισοσκελές με βάση α) τη ΒΓ β) τη ΑΒ γ) τη ΑΓ

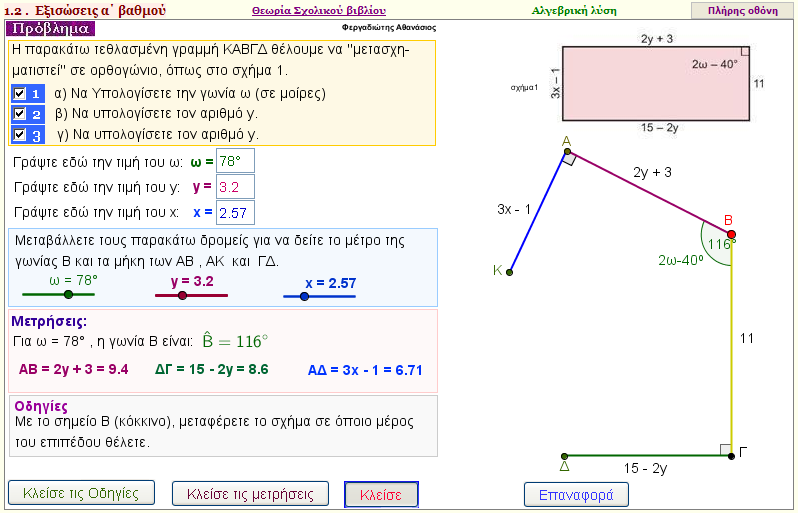
Άσκηση 11 Ένα ορθογώνιο έχει γωνία Β = 2ω - 40⁰ , απέναντι πλευρές 11 , 3χ - 1 και 2y + 3 ,15 - 2y . Να βρεθεί τις τιμές των ω , x , y.

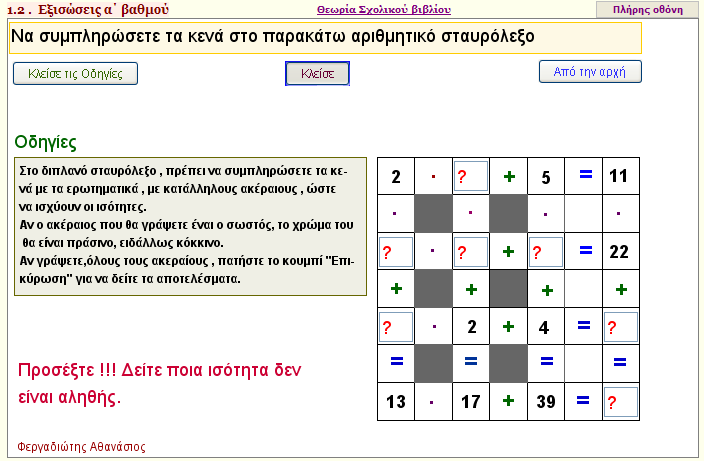
Διασκέδαση 1 Nα συμπληρώσετε τα κενά στο αριθμητικό σταυρόλεξο.

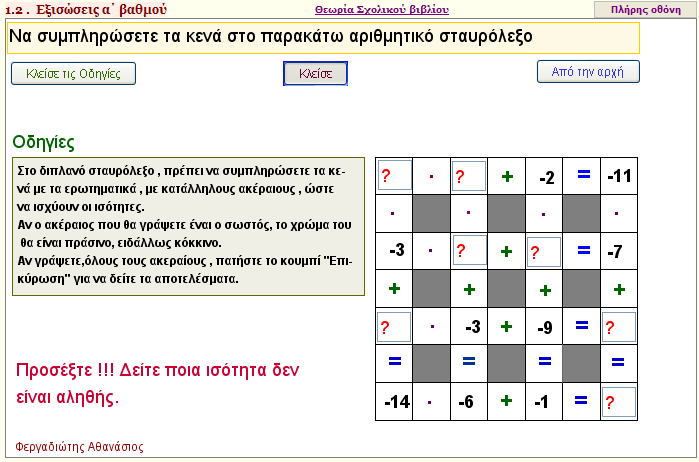
Διασκέδαση 2 Nα συμπληρώσετε τα κενά στο αριθμητικό σταυρόλεξο.