Α - Κεφάλαιο 2 - 2.2 Άρρητοι αριθμοί

Α - Κεφάλαιο 2 - 2.2 Άρρητοι αριθμοί - Πραγματικοί

2.2 - Άρρητοι αριθμοί - Πραγματικοί αριθμοί

Θεωρία			Ασκήσεις
Πακέτο θεωρίας σχολικού βιβλίου			Λύσεις ασκήσεων σχολικού βιβλίου και ερωτήσεων κατανόησης

Εφαρμογές
Προσέγγιση άρρητου αριθμού με έλλειψη και υπερβολή Υπολογίστε την τιμή ενός άρρητου αριθμού με: α) Προσέγγιση φυσικού με έλλειψη και υπερβολή β) Προσέγγιση δεκάτου με έλλειψη και υπερβολή γ) Προσέγγιση εκατοστού με έλλειψη και υπερβολή δ) Προσέγγιση χιλιοστού με έλλειψη και υπερβολή κ.λ.π

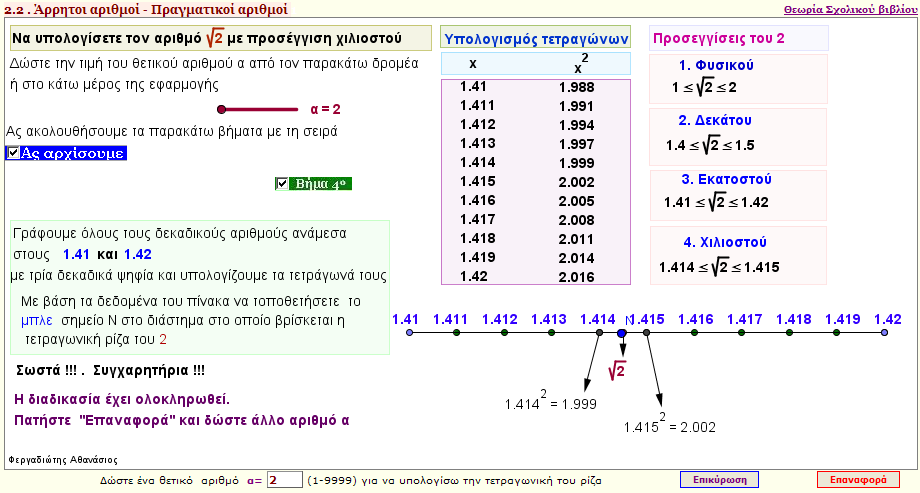
Προσέγγιση άρρητου αριθμού Υπολογίστε την τιμή ενός άρρητου αριθμού με προσέγγιση έως και εκατοντάκις χιλιοστού. Μπορείτε ναλύσετε τις ασκήσεις 2,3 και τις εφαρμογές 1 , 2 του βιβλίου σας

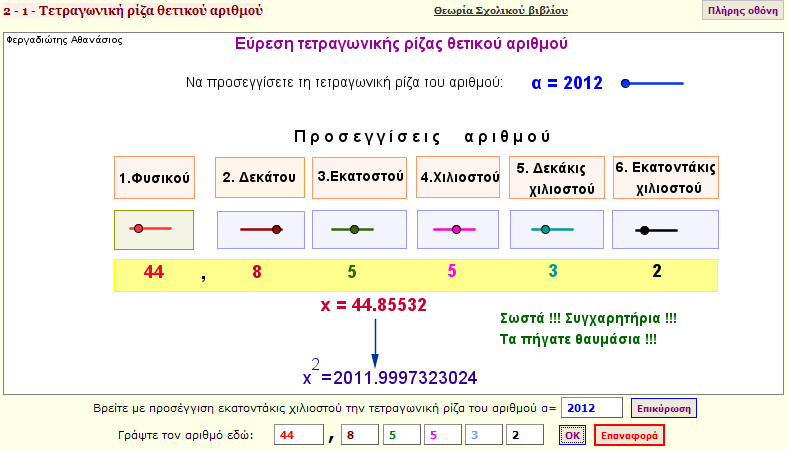
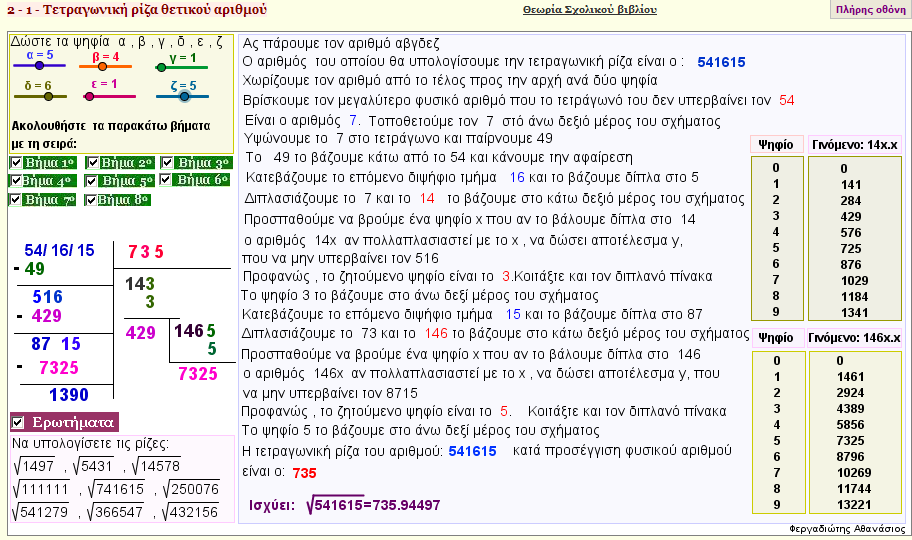
Αλγόριθμος εύρεσης τετραγωνικής ρίζας θετικού αριθμού Με ποιον τρόπο βρίσκουμε την τετραγωνική ρίζα ενός θετικού αριθμού α; Ο παραπάνω αλγόριθμος βρίσκει την τετραγωνική ρίζα ενός εξαψήφιου αριθμού. Ακολουθείστε ένα προς ένα τα βήματα της παραπάνω εφαρμογής.

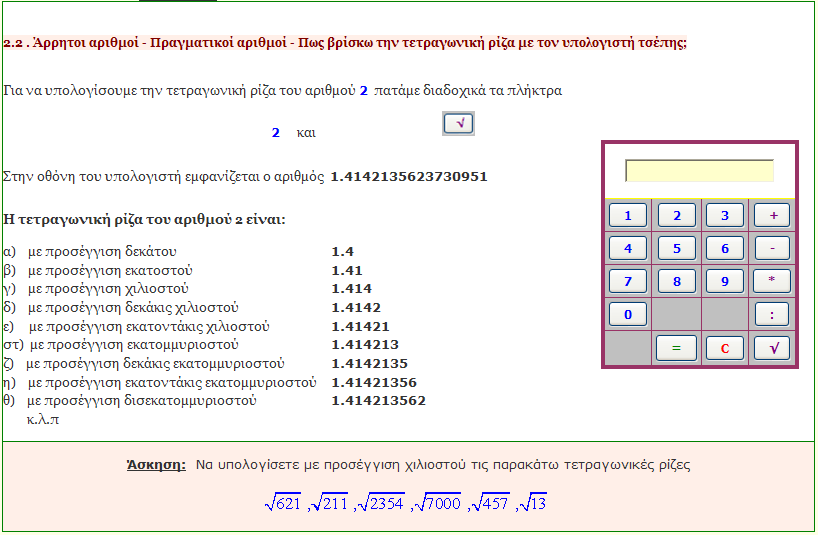
Yπολογισμός τετραγωνικής ρίζας με υπολογιστή τσέπης Χρησιμοποιείστε τον υπολογιστή τσέπης για να υπολογίστε την τετραγωνική ρίζα ενός αριθμού. Υπολογίστε την τεταγωνική ρίζα των αριθμών: α) 185 με προσέγγιση δεκάτου με έλλειψη και υπερβολή β) 193 με προσέγγιση εκατοστού με έλλειψη και υπερβολή γ) 17 με προσέγγιση χιλιοστού με έλλειψη και υπερβολή

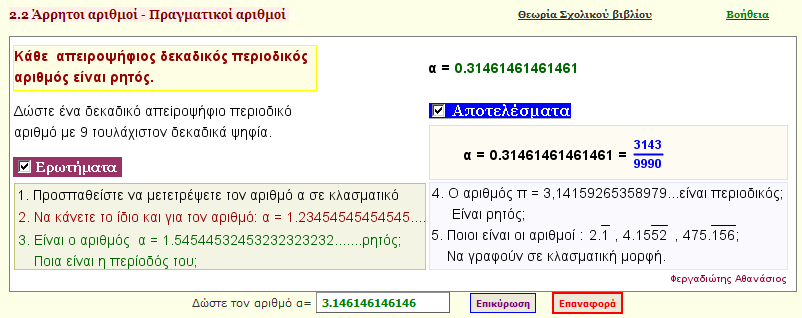
Mετατροπή απειροψήφιου δεκαδικού περιοδικού αριθμού σε κλασματικό Μετατρέψτε ένα απειροψήφιο δεκαδικό περιοδικό αριθμό σε κλασματικό. Υπολογίστε σε κλασματική μορφή τους αριθμούς: α) 2.3434343434343434.... β) 0.456565656565656.... γ) 12.3457897897897897897897......

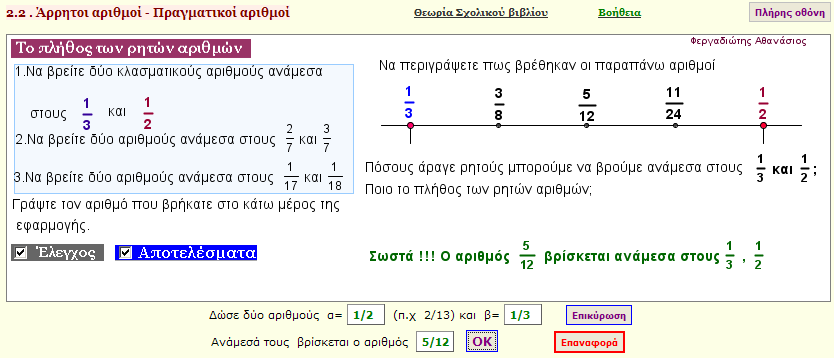
To πλήθος των ρητών αριθμών Πόσοι άραγε είναι οι ρητοί αριθμοί; Αν μας δώσουν δύο κλασματικούς αριθμούς , πόσοι άλλοι βρίσκονται ανάμεσά τους; Δύο μοντέλα για να βρίσκετε άλλους κλασματικούς αριθμούς ανάμεσα σε δύο δοσμένους κλασματικούς αριθμούς.

Yπολογισμός τετραγωνικής ρίζας -Eφαρμογή 2 Χρησιμοποιείστε τον υπολογιστή τσέπης για να υπολογίστε την τετραγωνική ρίζα ενός αριθμού. Υπολογίστε την τεταγωνική ρίζα των αριθμών: α) 3 με προσέγγιση δεκάτου με έλλειψη και υπερβολή β) 50 με προσέγγιση εκατοστού με έλλειψη και υπερβολή γ) 72 με προσέγγιση χιλιοστού με έλλειψη και υπερβολή δ) 1764 με προσέγγιση χιλιοστού με έλλειψη και υπερβολή ε) 427 με προσέγγιση χιλιοστού με έλλειψη και υπερβολή

H πραγματική ευθεία - Εφαρμογή 3 Αν σας δοθούν μερικοί αριθμοί, μπορείτε να τους τοποθετήσετε στην ευθεία των πραγματικών αριθμών;

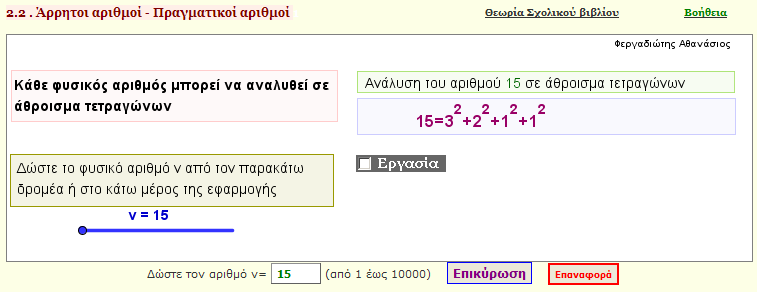
Aνάλυση φυσικού αριθμού σε άθροισμα τετραγώνων Δώστε ένα φυσικό αριθμό και αναλύστε τον σε άθροισμα τετραγώνων. Η ανάλυση αυτή είναι χρήσιμη για την κατασκευή άρρητων αριθμών.

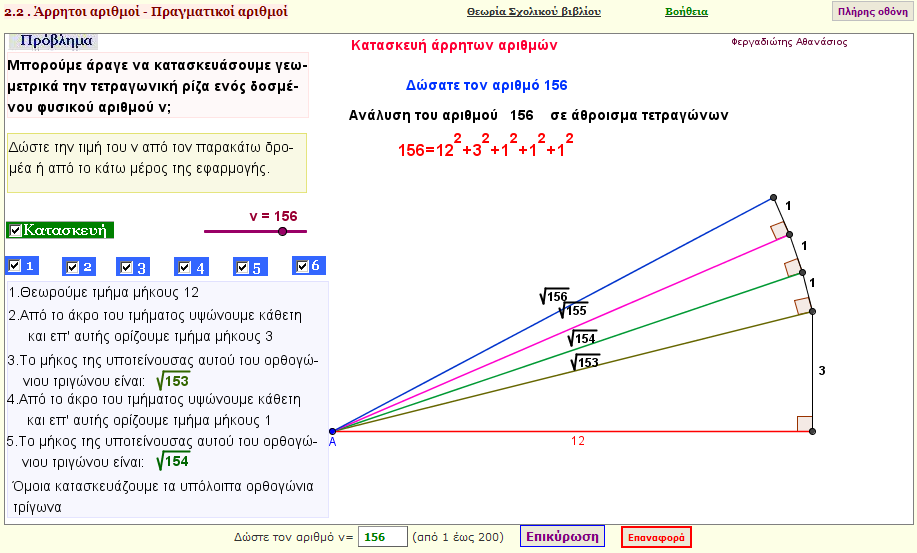
Γεωμετρική κατασκευή άρρητων αριθμών Είναι γνωστό , οτι κάθε φυσικός αριθμός αναλύεται σε άθροισμα τετραγώνων άλλων φυσικών αριθμών. Χρησιμοποιώντας την παραπάνω πρόταση , μπορούμε να κατασκευάσουμε γεωμετρικά (με τη χρήση ορθογώνιων τριγώνων) άρρητους αριθμούς. Να κατασκευάσετε γεωμετρικά τους παρακάτω αριθμούς: $ \sqrt{5} $ , $ \sqrt{17} $ , $ \sqrt{111} $ , $ \sqrt{93} $ , $ \sqrt{57} $ , $ \sqrt{32} $ , $ \sqrt{177} $ , $ \sqrt{151} $

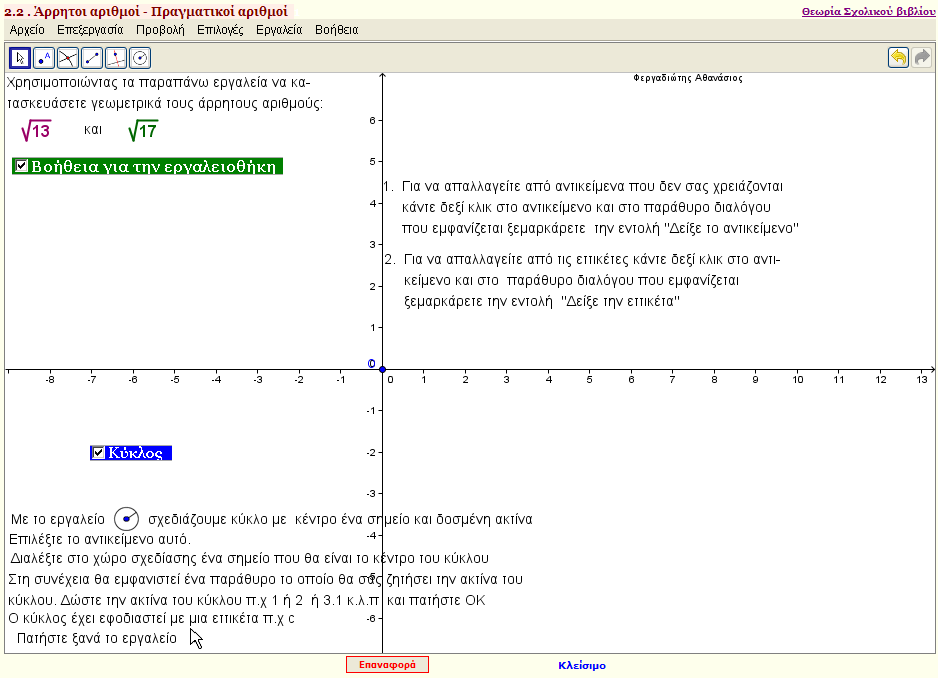
Kατασκευάστε μόνοι σας άρρητους αριθμούς Σας δίνονται μερικά εργαλεία και με την βοήθεια αυτών σας ζητείται η κατασκευή , με γεωμετρικό τρόπο, άρρητων αριθμών. Διαβάστε προσεκτικά τις βοήθειες των ''εργαλείων''.

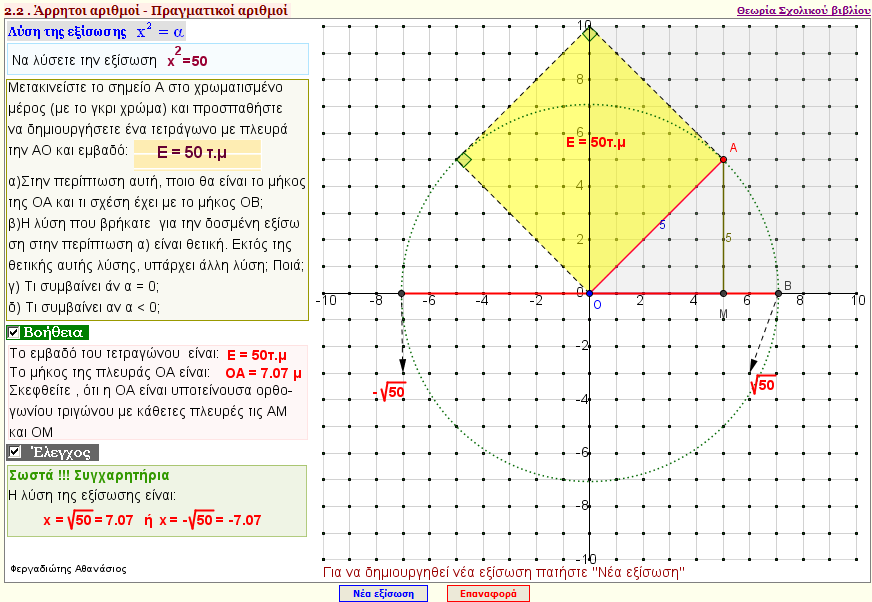
Άσκηση4 Με την εφαρμογή αυτή λύνουμε τις εξισώσεις π.χ x² = 0 , x² = 5 , x² = -3 , x² = 17 με γεωμετρικό τρόπο.

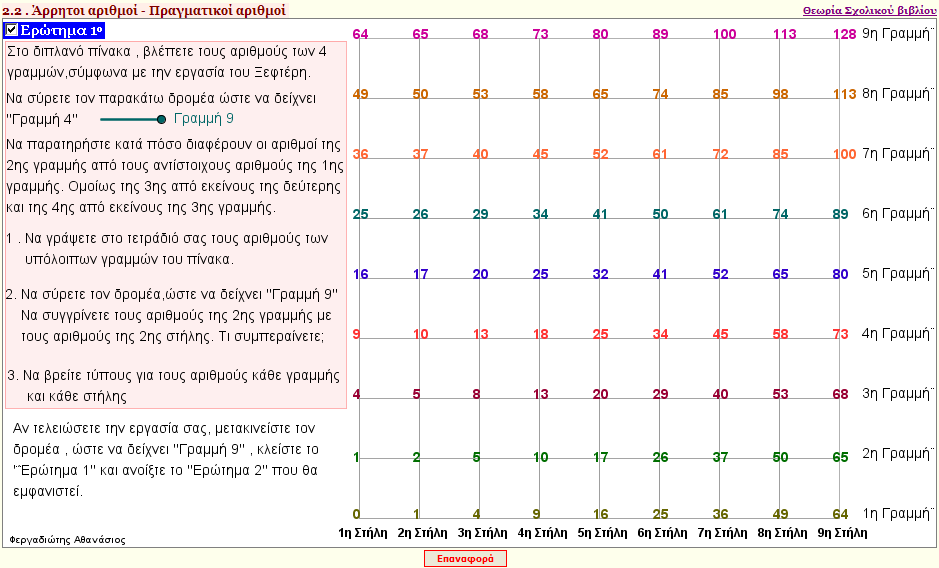
Eργασία Ξεφτέρη Με ποιον τρόπο ο Ξεφτέρης σχεδιάζει άρρητους αριθμούς; Σχέσεις μεταξύ αυτών των αριθμών . Συμπεράσματα Ξεφτέρη.